Abstract
Nowadays, high performance concrete is used more frequently because of the many advantages compared to traditional concrete. The higher mechanical properties (e.g., compressive strength, flexural strength, and Young’s modulus) allow for larger spans and slender cross-sections. Despite the use of advanced material, standards for structural design do not fully use materials’ potential. This can be minimized by using fracture mechanical properties in structural analysis. The fracture mechanical properties help to perform advanced structural analysis, especially when some of the structural elements have a crack. The load presence on the structure can be divided into tensile—mode I, shear—mode II, and combination of tension and shear—mixed mode I/II load. Therefore, it is necessary to perform test, which covers mixed mode loading conditions. One of the tests usually used for the evaluation of fracture resistance of concrete is Brazilian disc test. This contribution compares fracture resistance of two types of structural concrete (normal and high strength) under the mixed mode I/II. The generalized maximum tangential stress (GMTS) criterion was used for the evaluation of the fracture resistance.
1. Introduction
The design of concrete structural elements used in civil engineering is optimized to reduce material consumption and to improve structural behavior. However, the traditional concrete does not satisfy increasing demands on the structural and material performance. Therefore, new materials are developed with focus on mechanical performance such as compressive strength, flexural strength, and Young’s modulus. The use of concrete with high compressive strength (HSC) [1] in structural design can provide slenderer cross-section, which leads into reducing total material consumption with retaining similar mechanical performance of the structure.
The advanced structural analysis uses fracture mechanical properties as an input parameter to predict total structural service life time and fracture resistance. The structural elements after certain time can show minor surface damage or shrinkage can create micro-cracks. These defects are zones of weakness, where the crack can initiate. The load presence on the structural element can be characterized by tensile mode I and shear mode II. In reality, some cracks are loaded by combination of tension and shear—mixed mode I/II load. Hence, it is necessary to test material under the mixed mode loading conditions [2,3,4]. One of the tests usually used for evaluation of fracture resistance of concrete is Brazilian disc [5,6].
The aim of this contribution is to evaluate and compare the fracture resistance of two concrete types used for precast structural elements under the mixed mode load. The first one is traditional concrete with grade C 50/60 and the second type is HSC concrete with compressive strength around 100 MPa. The assessment of the fracture resistance of both studied materials, is evaluated from the experimental results by employing fracture resistance curve calculated from the generalized maximum tangential stress (GMTS) criterion, which is based on two-parameter linear elastic fracture mechanics. The results are compared and discussed.
2. Theoretical Background
This contribution is based on a linear elastic fracture mechanics. The linear elastic fracture mechanics concept uses the stress field in the close vicinity of the crack tip described by Williams expansion [7]. This expansion is an infinite power series originally derived for a homogenous elastic isotropic cracked body. The stress field for mode I and mode II can be described by a following equation:
where σij represents the stress tensor components, KI, KII are the stress intensity factors (SIF) for mode I and mode II, respectively, , , are known shape functions for mode I and mode II usually written as YI and YII, T (or T-stress) represents the second term independent on r, Oij represents higher order terms, and r, θ are the polar coordinates (with origin at the crack tip; crack faces lie along the x-axis).
2.1. Brazilian Disc Test
Brazilian disc test with a central notch (BDC) is specimen with circular cross section, made from the cylinder with a notch in the middle of specimen (see Figure 1a) [8,9,10]. The test performed on the BDC specimen is carried out under relatively simple experimental conditions (see Figure 1b), using only the testing press with sufficient load capacity. The evaluation of the fracture parameters for modes I, II and mixed mode I/II is done by inclining the notch by angle α against the load position.

Figure 1.
Brazilian disc with central notch—principle of testing (a) and actual test setup (b).
The SIF for a finite specimen in shape of Brazilian disc and the polar angle θ = 0° can be calculated by following equations [11,12]:
where P is compressive load, a is a crack length, R is radius of the disc (D/2), B is disc thickness, α is inclination angle and YI(a/R, α), YII(a/R, α) are dimensionless shape functions for mode I and mode II, respectively. Geometry functions YI and YII used in Equations (2) and (3) can be found in [8,9].
To calculate T-stress, a direct extrapolation method [13] is used, for polar angle θ = 0° the following equation is used:
where σxx and σyy are the stress components in front of the crack tip in direction for θ = 0°.
2.2. GMTS Criterion
There are several criteria for predicting the onset of mixed mode fracture of brittle materials. The criteria which can be used on the BDC specimen the maximum tangential stress (MTS) criterion [14] and the minimum strain energy density (SED) criterion [15]. However, these criteria are not able to accurately predict onset of mix mode fracture. These disadvantages lead to the development of the generalized maximum tangential stress (GMTS) criterion [16]. The GMTS criterion has been recently used to the fracture resistance of the BDC specimen by Aliha et al. [17] for PMMA and Hou et al. [18] for mortar and concrete. All studies displayed an accurate prediction of fracture resistance.
According to the first hypothesis of the GMTS criterion, the onset of fracture is the angle of maximum tangential stress θ0 and can be determined from:
Assumption mentioned in Equation (5) leads into:
Crack initiation angle θ0 is then used for evaluation of beginning of mixed mode I/II on BDC specimen.
Application of the GMTS on Brazilian Disc Specimen
Pure mode I fracture initiation appears when KI = KIC, KII = 0 and θ0 = 0°, this assumption leads into Equation (7):
where KIC is materials’ fracture toughness. Fracture resistance for both modes is expressed by ratio KI/KIC and KII/KIC. This ratio is obtained from Equation (7) by dividing the whole expression by KI, KII, respectively.
Equation (6) shows that the angle θ0 for any combination of modes I and II depends on KI, KII, T, and rC. Critical distance rC can be evaluated from Equations (8) and (9) for plane stress and plane strain respectively [11].
3. Materials
3.1. Normal Strength Concrete
The C 50/60 concrete type was chosen for the study because it is typically used for the pre-stressed precast elements which are produced nowadays. The studied concrete contains 450 kg of CEM I 42.5 R, the water to cement ratio c/w is 0.40. Fine aggregate was natural sand 0/4 mm and crushed aggregates 4/8 mm and 8/16 mm from high quality granite was used as well as drinking water. The concrete was mixed in a volume of 1 m3 and poured immediately into molds. A polycarboxylates-based superplasticizer was used to reach good workability [10].
3.2. High Strength Concrete
High strength concrete was designed with intent to produce subtle elements. The maximum size of aggregate was chosen 8 mm. The aggregates were composed from natural sand 0/4 mm and crushed high quality granite 4/8 mm. Portland cement CEM I 42.5 R was used with three mineral admixtures. The first, was metakaolin, with strong pozzolanic properties. The second and third admixture were chosen to reach synergy in ternary binders [19] based on experiments, see for example [20]. Generally, binder consist 81% of CEM I 42.5 R, 9.5% of metakaolin, 7.5% of GBFS and 2.5% of limestone. Water/binder ratio was 0.22. A polycarboxylate based superplasticizer was selected based on its compatibility with cement. The concrete was mixed in volume 0.7 m3 and poured into molds.
4. Experimental Measurement
The machine for tests has a maximum loading capacity 200 kN, the speed of the induced displacement of the upper support was equal to 0.025 mm/s. BDC specimens with relative notch length a/R = 0.4 were inclined against loading positions under the selected angles. Table 1 and Table 2 give overview of the mean values of the specimen dimensions for C 50/60 and HSC, respectively.

Table 1.
Dimensions of BDC specimens made from C 50/60.

Table 2.
Dimensions of BDC specimens made from HSC.
5. Results and Discussion
Fracture mechanical properties (SIFs) of investigated materials were evaluated by using Equations (2) and (3). From Figure 2a it can be seen, that the fracture of HSC material is done under higher fracture force than for the C 50/60 material. The Figure 2b show fracture resistance of studied materials.
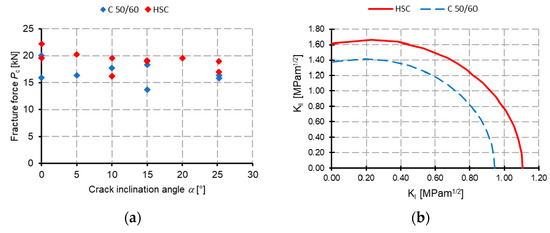
Figure 2.
Comparison of measured forces (a) and values of SIFs (b) for C 50/60 and HSC.
The comparison of experimental results is done by fracture resistance curves. Fracture resistance curves were calculated using Equation (7) for each material and its critical distance rC. From Figure 3 it can be noted, that the MTS criterion is very conservative for both materials. The GMTS criterion predict fracture resistance with great agreement especially for plane strain boundary conditions.
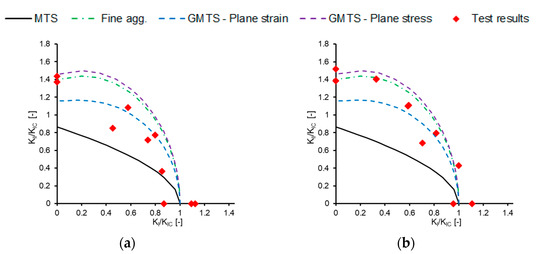
Figure 3.
Mixed mode fracture toughness diagram for C 50/60 (a) and HSC (b) materials, using various critical distances rC.
6. Conclusions
In this paper a fracture resistance of two concrete types C 50/60 and HSC was experimentally investigated by using Brazilian disc test. The mixed mode fracture resistance is evaluated by employing GMTS criterion. The following conclusions were found:
- The fracture toughness measured on the HSC material is higher in all investigated cases than for the traditional C 50/60 material.
- The experimental results done on the HSC material showed higher fracture resistance in mixed mode I/II than the traditional C 50/60 material.
- The fracture resistance of the C 50/60 material is characterized best by rC for plain strain, yet for HSC, it is better to use value of rC for fine aggregate.
Author Contributions
P.M. and S.S. performed the experiments and analyzed the experimental data from BDC specimen; V.B. provides material’s composition.
Acknowledgments
This paper has been written with financial support from the FAST-J-18-5164 supported by the Ministry of Education, Youth and Sports of the Czech Republic and Brno University of Technology. The first author is Brno Ph.D. Talent Scholarship Holder—Funded by the Brno City Municipality.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nawy, E.G. Fundamentals of High-Performance Concrete; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Malíková, L.; Veselý, V.; Seitl, S. Crack propagation direction in a mixed mode geometry estimated via multi-parameter fracture criteria. Int. J. Fatigue 2016, 89, 99–107. [Google Scholar] [CrossRef]
- Fett, T.; Gerteisen, G.; Hahnenberger, S.; Martin, G.; Munz, D. Fracture tests for ceramics under mode-I, mode-II and mixed-mode loading. J. Eur. Ceram. Soc. 1995, 15, 307–312. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Aliha, M.R.M.; Saghafi, H. An improved semi-circular bend specimen for investigating mixed mode brittle fracture. Eng. Fract. Mech. 2011, 78, 110–123. [Google Scholar] [CrossRef]
- Li, D.; Wong, L.N.Y. The brazilian disc test for rock mechanics applications: Review and new insights. Rock Mech. Rock Eng. 2013, 46, 269–287. [Google Scholar] [CrossRef]
- Atkinson, C.; Smelser, R.E.; Sanchez, J. Combined mode fracture via the cracked brazilian disk test. Int. J. Fract. 1982, 18, 279–291. [Google Scholar] [CrossRef]
- Williams, M.L. On the stress distribution at the base of a stationary crack. J. Appl. Mech. 1956, 24, 6. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Aliha, M.R.M. On the use of brazilian disc specimen for calculating mixed mode I-II fracture toughness of rock materials. Eng. Fract. Mech. 2008, 75, 4631–4641. [Google Scholar] [CrossRef]
- Seitl, S.; Miarka, P. Evaluation of mixed mode I/II fracture toughness of C 50/60 from Brazilian disc test. Frattura ed Integrita Strutturale 2017, 11, 119–127. [Google Scholar] [CrossRef]
- Seitl, S.; Miarka, P.; Bílek, V. The mixed-mode fracture resistance of C 50/60 and its suitability for use in precast elements as determined by the brazilian disc test and three-point bending specimens. Theor. Appl. Fract. Mech. 2018, in press. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Tada, H.; Paris, P.C.; Irwin, G.R. The Stress Analysis of Cracks Handbook, 3rd ed.; ASM Press: New York, NY, USA, 2000. [Google Scholar]
- Yang, B.; Ravi-Chandar, K. Evaluation of elastic T-stress by the stress difference method. Eng. Fract. Mech. 1999, 64, 589–605. [Google Scholar] [CrossRef]
- Erdogan, F.; Sih, G.C. On the crack extension in plates under plane loading and transverse shear. J. Basic Eng. 1963, 85, 519–525. [Google Scholar] [CrossRef]
- Sih, G.C. Strain-energy-density factor applied to mixed mode crack problems. Int. J. Fract. 1974, 10, 305–321. [Google Scholar] [CrossRef]
- Smith, D.J.; Ayatollahi, M.R.; Pavier, M.J. The role of T-stress in brittle fracture for linear elastic materials under mixed-mode loading. Fatigue Fract. Eng. Mater. Struct. 2001, 24, 137–150. [Google Scholar] [CrossRef]
- Aliha, M.R.M.; Bahmani, A.; Akhondi, S. Mixed mode fracture toughness testing of pmma with different three-point bend type specimens. Eur. J. Mech.—A/Solids 2016, 58, 148–162. [Google Scholar] [CrossRef]
- Hou, C.; Wang, Z.; Liang, W.; Li, J. Determination of fracture parameters in center cracked circular discs of concrete under diametral loading: A numerical analysis and experimental results. Theor. Appl. Fract. Mech. 2016, 85, 355–366. [Google Scholar] [CrossRef]
- Adu-Amankwah, S.; Zajac, M.; Stabler, C.; Lothenbach, B. Influence of limestone on the hydration of ternary slag cements. Cem. Concr. Res. 2017, 100, 96–109. [Google Scholar] [CrossRef]
- Bilek, V.; Pytlik, D.; Bambuchova, M. High-Performance Concrete with Ternary Binders. Key Eng. Mater. 2018, 761, 120–123. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).