Durability of Composite Materials under Severe Temperature Conditions: Influence of Moisture Content and Prediction of Thermo-Mechanical Properties During a Fire
Abstract
:1. Introduction
2. Materials and Methods
2.1. Thermal Model Development
2.2. Post-Combustion Mechanical Response
3. Results
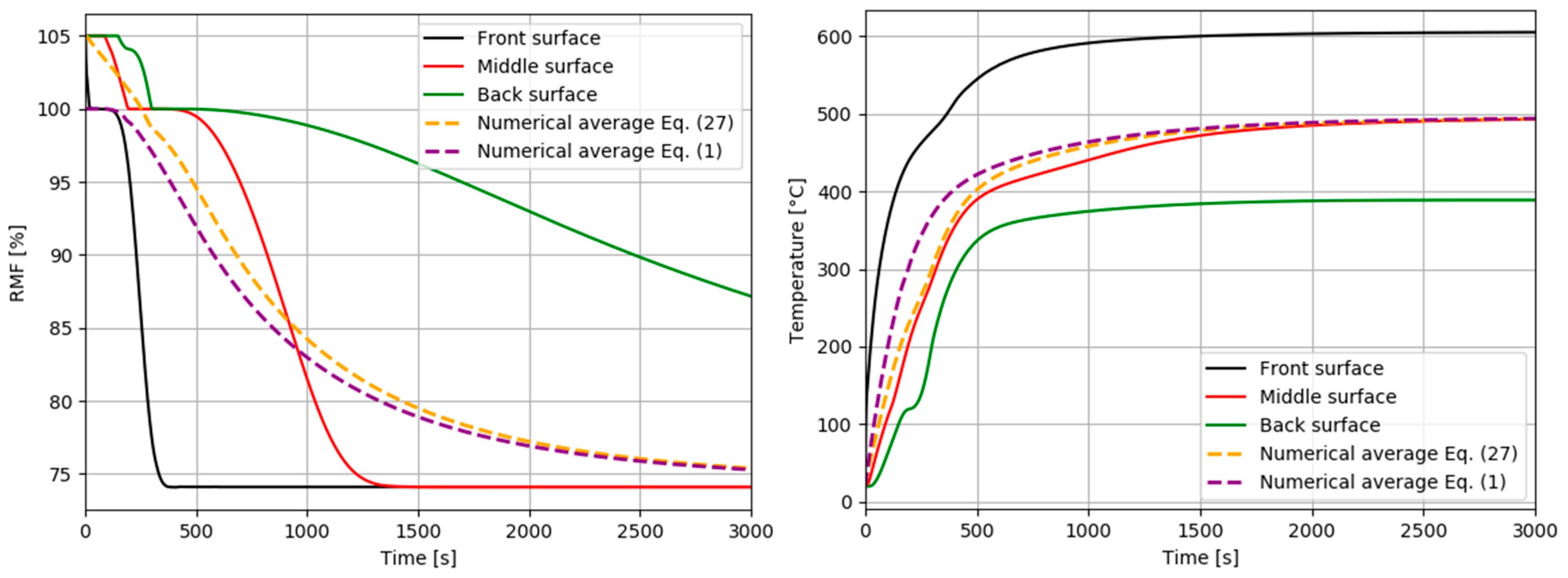
3.1. Thermal Degradation Prediction
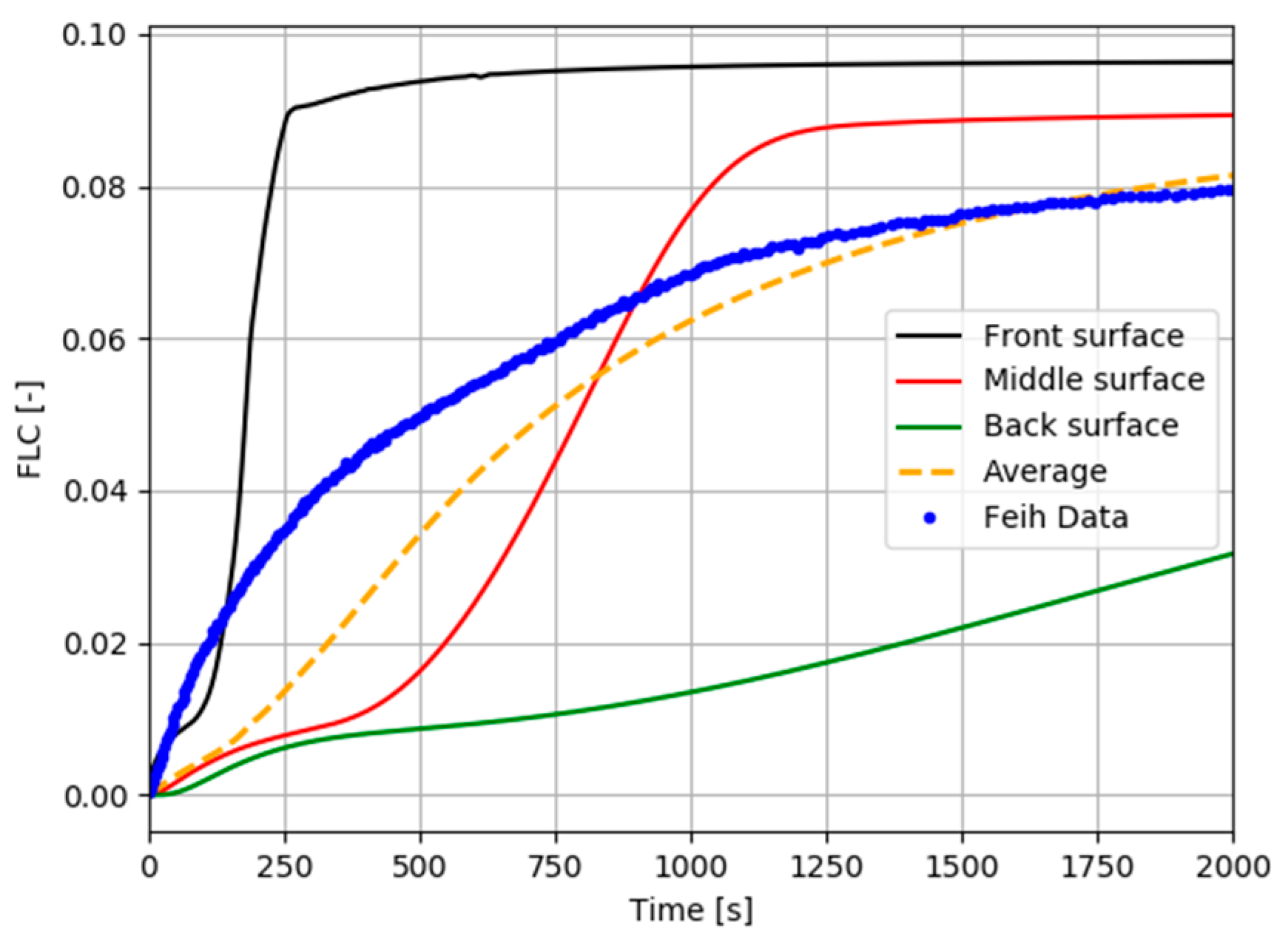
3.2. Mechanical Properties Prediction
4. Discussion: Hygro-Thermal Durability in Fire Conditions
4.1. Hygro-Thermal Model Development
4.2. Hygro-Thermo-Mechanical Durability
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | Pre-exponential factor of Arrhenius law (s−1) |
| ci | Specific heat of state i (J·kg−1·K−1) |
| cp | Specific heat of the material (J·kg−1·K−1) |
| cpg | Specific heat of gas (J·kg−1·K−1) |
| Specific heat of water vapor (J·kg−1·K−1) | |
| d | Total thickness (m) |
| dc | Carbonized layer thickness (m) |
| dn | Balance bending forces’ thickness (m) |
| Ea | Activation energy (J·mol−1) |
| E | Young modulus (MPa) |
| <EI> | Flexural modulus (MN·m2) |
| fc | Correction factor (-) |
| hg | Enthalpy of pyrolysis gases (J·kg−1) |
| hs | Enthalpy of the solid material (J·kg−1) |
| hconv | Convective heat transfer coefficient (W·m−2·K−1) |
| I | Quadratic moment (m4) |
| kg | Thermal conductivity of volatile gases (W·m−1·K−1) |
| ki | Thermal conductivity of state i (W·m−1·K−1) |
| kx | Thermal conductivity of solid material (W·m−1·K−1) |
| L | Thickness of material (m) |
| mg | Volatile gases mass (kg) |
| Mass flow rate per unit area of pyrolysis gases through the reaction zone (kg·s−1·m−2) | |
| mm | Mass of matrix (kg) |
| ms | Solid mass of material (kg) |
| Water mass (kg) | |
| M | Average molecular weight of gases (kg·mol−1) |
| n | Order of decomposition reaction |
| P | Internal pressure of gases (atm) |
| Heat flux (W·m−2) | |
| Qp | Heat of decomposition (J·kg−1) |
| R | Ideal gas constant (8.314 J·mol−1·K−1) |
| t | Time (s) |
| T | Temperature (K) |
| T∞ | Ambient temperature (K) |
| Vf | Volume fraction of fibres (%) |
| Vm | Volume fraction of the matrix (%) |
| x | Through-thickness coordinate (m) |
| X | Mass fraction (-) |
| α | Remaining mass fraction of virgin material (-) |
| αi | Linear thermal expansion coefficient of state i (K−1) |
| γ | Permeability of material (m2) |
| Δhfg | Latent heat of water (J·kg−1) |
| Δhl | Evaporation heat of free liquid water (J·kg−1) |
| Δhdesorp | Evaporation heat of bound water (J·kg−1) |
| ψi | Permeability coefficient of state i (K−1) |
| εm | Material surface emissivity (-) |
| εs | Source emissivity (-) |
| ζ | Dimensionless expansion factor (-) |
| η | Dimensionless permeability factor (-) |
| μ | Gases viscosity (Pa·s) |
| ρ | Material density (kg·m−3) |
| σ | Stefan-Boltzmann constant (5.67 × 108 W·m−2·K−4) |
| Φ | Porosity of material (-) |
| Subscripts | |
| a | Activation |
| c | Carbonized state |
| composite | Composite |
| conv | Convection |
| 0 | Initial state |
| f | Final state |
| fiber | Fiber |
| fsp | Fiber saturation point |
| g | Gas |
| Water | |
| inf | Inferior |
| m | Matrix |
| p | Pyrolysis |
| s | Sample material |
| sat | Saturation |
| sup | Superior |
| v | Virgin state |
| Water vapor | |
| Acronyms | |
| PDE | Partial Differential Equation |
| ODE | Ordinary Differential Equation |
| DAE | Differential Algebraic equation |
| RMF | Remaining Mass Fraction |
| FLC | Fraction Length Change |
References
- Legrand, V.; Merdrignac-Conanec, O.; Paulus, W.; Hansen, T. Study of the thermal nitridation of nanocrystalline Ti(OH)4 by X-ray and in situ neutron powder diffraction. J. Phys. Chem. A 2012, 116, 9561–9567. [Google Scholar] [CrossRef]
- Legrand, V.; Pillet, S.; Weber, H.P.; Souhassou, M.; Létard, J.-F.; Guionneau, P.; Lecomte, C. On the precision and accuracy of structural analysis of light induced metastable states. J. Appl. Crystallogr. 2007, 40, 1076–1088. [Google Scholar] [CrossRef]
- Legrand, V.; Pillet, S.; Carbonera, C.; Souhassou, M.; Létard, J.-F.; Guionneau, P.; Lecomte, C. Optical, magnetic and structural properties of the spin crossover complex [Fe(btr)2(NCS)2].H2O in the light-induced and thermally quenched metastable states. Eur. J. Inorg. Chem. 2007, 5693–5706. [Google Scholar] [CrossRef]
- Legrand, V.; Carbonera, C.; Pillet, S.; Souhassou, M.; Létard, J.-F.; Guionneau, P.; Lecomte, C. Photocrystallography: From the structure towards the electron density of metastable states. J. Phys. Conf. Ser. 2005, 21, 73–80. [Google Scholar] [CrossRef]
- Gloaguen, D.; Oum, G.; Legrand, V.; Fajoui, J.; Moya, M.J.; Pirling, T.; Kockelmann, W. Intergranular strain evolution in titanium during tensile loading: Neutron diffraction and polycristalline model. Metall. Mater. Trans. A 2015, 46, 5038–5046. [Google Scholar] [CrossRef]
- Hounkpati, V.; Fréour, S.; Gloaguen, D.; Legrand, V.; Kelleher, J.; Kockelmann, W.; Kabra, S. In situ neutron measurements and modelling of the intergranular strains in the near- titanium alloy Ti-β21S. Acta Mater. 2016, 109, 341–352. [Google Scholar] [CrossRef]
- Legrand, V.; Kockelmann, W.; Frost, C.D.; Hauser, R.; Kaczorowski, D. Neutron diffraction study of the non-Fermi liquid compound CeNiGa2: Magnetic behaviour as a function of pressure and temperature. J. Phys. Condens. Matter 2013, 25, 206001. [Google Scholar] [CrossRef]
- Legrand, V.; Le Gac, F.; Guionneau, P.; Létard, J.-F. Neutron powder diffraction studies of two spin transition Fe(II)-complexes under pressure. J. Appl. Crystallogr. 2008, 41, 637–640. [Google Scholar] [CrossRef]
- Legrand, V.; Pechev, S.; Létard, J.-F.; Guionneau, P. Synergy between polymorphism, pressure, spin-crossover and temperature in [Fe(PM-BiA)2(NCS)2]: A neutron powder diffraction investigation. Phys. Chem. Chem. Phys. 2013, 15, 13872–13880. [Google Scholar] [CrossRef]
- Legrand, V.; Pillet, S.; Souhassou, M.; Lugan, N.; Lecomte, C. Extension of the experimental electron density analysis to metastable states: A case example of the spin crossover complex Fe(btr)2(NCS)2.H2O. J. Am. Chem. Soc. 2006, 128, 13921–13931. [Google Scholar] [CrossRef]
- Rizk, G.; Legrand, V.; Khalil, K.; Casari, P.; Jacquemin, F. Durability of sandwich composites under extreme conditions: Towards the prediction of fire resistance properties based on thermo-mechanical measurements. Compos. Struct. 2018, 186, 233–245. [Google Scholar] [CrossRef]
- Mouritz, A.P.; Gibson, A.G. Fire Properties of Polymer Composite Materials, Solid Mechanics and Its Applications; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Henderson, J.B.; Wiebelt, J.A.; Tant, M.R. A model for the thermal response of polymer composite materials with experimental verification. J. Compos. Mater. 1985, 19, 579–595. [Google Scholar] [CrossRef]
- Gibson, A.G.; Wu, Y.-S.; Chandler, H.W.; Wilcox, J.A.D.; Bettess, P. A model for the thermal performance of thick composite laminates in hydrocarbon fires. Rev. L’Inst. Fr. Pét. 1995, 50, 69–74. [Google Scholar] [CrossRef]
- Henderson, J.B.; Wiecek, T.E. A Mathematical Model to Predict the Thermal Response of Decomposing, Expanding Polymer Composites. J. Compos. Mater. 1986, 21, 373–393. [Google Scholar] [CrossRef]
- Buch, J.D. Thermal Expansion Behavior of a Thermally Degrading Organic Matrix Composite. In Thermomechanical Behavior of High-Temperature Composites; ASME Publication AD-04; ASME: New York, NY, USA, 1982. [Google Scholar]
- Lattimer, B.Y.; Ouellette, J.; Trelles, J. Thermal Response of Composite Materials to Elevated Temperatures. Fire Technol. 2011, 47, 823–850. [Google Scholar] [CrossRef]
- Ramroth, W.T. Thermo-Mechanical Structural Modelling of FRP Composite Sandwich Panels Exposed to Fire. Ph.D. Thesis, UC San Diego, San Diego, CA, USA, 2006. [Google Scholar]
- The Numerical Method of Lines. Available online: https://reference.wolfram.com/language/tutorial/NDSolveMethodOfLines.html (accessed on 1 September 2017).
- Mouritz, A.P.; Mathys, Z. Post-fire mechanical properties of marine polymer composites. Compos. Struct. 1999, 47, 643–653. [Google Scholar] [CrossRef]
- Mouritz, A.P.; Mathys, Z. Post-fire mechanical properties of glass-reinforced polyester composites. Compos. Sci. Technol. 2001, 61, 475–490. [Google Scholar] [CrossRef]
- Mouritz, A.P.; Feih, S.; Kandare, E.; Mathys, Z.; Gibson, A.G.; Des Jardin, P.E.; Case, S.W.; Lattimer, B.Y. Review of fire structural modelling of polymer composites. Compos. Part A 2009, 40, 1800–1814. [Google Scholar] [CrossRef]
- Theulen, J.C.M.; Peijs, A.A.J.M. Optimization of the bending stiffness and strength of composite sandwich panels. Compos. Struct. 1991, 17, 87–92. [Google Scholar] [CrossRef] [Green Version]
- Feih, S.; Mathys, Z.; Gibson, A.G.; Mouritz, A.P. Modelling the compression strength of polymer laminates in fire. Compos. Part A 2007, 38, 2354–2365. [Google Scholar] [CrossRef]
- Zhuge, J.; Gou, J.; Chen, R.-H.; Kapat, J. Finite element modeling of post-fire flexural modulus of fiber reinforced polymer composites under constant heat flux. Compos. Part A 2012, 43, 665–674. [Google Scholar] [CrossRef]
- Overall Heat Transfer Coefficient. Available online: https://www.engineeringtoolbox.com/overall-heat-transfer-coefficient-d_434.html (accessed on 1 September 2017).
- Vinyl Ester Systems. Available online: https://www.epoxy.com/vester.htm (accessed on 1 September 2017).
- Goodrich, T.W.; Lattimer, B.Y.; Case, S.W.; Ellis, M.W. Thermophysical Properties and Microstructural Changes of Composite Materials at Elevated Temperature. Ph.D. Thesis, Faculty of the Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2009. [Google Scholar]
- Polyester Resins. Available online: http://www.exelcomposites.com/fi-fi/english/composites/rawmaterials/resins.aspx (accessed on 1 September 2017).
- Mouritz, A.P.; Feih, S.; Kandare, E.; Mathys, Z.; Gibson, A.G.; Des Jardin, P.; Case, S.; Lattimer, B. Damage and failure modelling of fibre-polymer composite in fire. Int. Conf. Compos. Mater. 2009. [Google Scholar]
- Youssef, G.; Fréour, S.; Jacquemin, F. Stress-dependent Moisture Diffusion in Composite Materials. J. Compos. Mater. 2009, 43, 1621–1637. [Google Scholar] [CrossRef]
- Ramezani Dana, H.; Jacquemin, F.; Fréour, S.; Perronnet, A.; Casari, P.; Lupi, C. Numerical and experimental investigation of hygro mechanical states of glass fiber reinforced polyester composites experienced by FBG sensors. Compos. Struct. 2014, 116, 38–47. [Google Scholar] [CrossRef] [Green Version]
- Ibrahim, G.; Casari, P.; Jacquemin, F.; Fréour, S.; Clement, A.; Célino, A.; Khalil, K. Moisture diffusion in composites tubes: Characterization and identification of microstructure-properties relationship. J. Compos. Mater. 2018, 52, 1073–1088. [Google Scholar] [CrossRef]
- Shi, X.; Xiao, H.; Liao, X.; Armstrong, M.; Chen, X.; Lackner, K.L. Humidity effect on ion behaviors of moisture-driven CO2 sorbents. J. Chem. Phys. 2018, 149, 164708. [Google Scholar] [CrossRef] [PubMed]
- Peters, B.; Bruch, C. A flexible and stable numerical method for simulating the thermal decomposition of wood particles. Chemosphere 2001, 42, 481–490. [Google Scholar] [CrossRef]
- Bryden, K.M.; Ragland, K.W.; Rutland, C.J. Modeling thermally thick pyrolysis of wood. Biomass Bioenergy 2002, 22, 41–53. [Google Scholar] [CrossRef]
- Shi, L.; Michael, Y.L.C. A review of fire processes modeling of combustible materials under external heat flux. Fuel 2013, 106, 30–50. [Google Scholar] [CrossRef]
- Sand, U.; Sandberg, J.; Larfeldt, J.; Bel Fdhila, R. Numerical prediction of the transport and pyrolysis in the interior and surrounding of dry and wet wood log. Appl. Energy 2008, 85, 1208–1224. [Google Scholar] [CrossRef]
- Looyeh, M.R.E.; Bettess, P. A Finite element model for the fire-performance of GRP panels including variable thermal properties. Finite Elem. Anal. Des. 1998, 30, 313–324. [Google Scholar] [CrossRef]












| Property | Value | Source |
|---|---|---|
| Volume fraction of fibers (-) | 0.55 | [24] |
| Kinetics rate constant (1/s) | 2 × 1013 | [24] |
| Activation energy (J/mol) | 2.12 × 105 | [24] |
| Reaction order (-) | 1 | [24] |
| Remaining matrix mass fraction (-) | 0.03 | [24] |
| Heat of decomposition of the matrix (J/kg) | 378,800 | [24] |
| Density of glass fiber (kg/m3) | 2560 | [24] |
| Density of vinyl ester (kg/m3) | 1140 | [24] |
| Thermal conductivity of glass fiber (W/(m·K)) | 1.09 | [24] |
| Thermal conductivity of vinyl ester (W/(m·K)) | 0.19 | [26] |
| Specific heat of glass fiber (J/(kg·K)) | 760 | [24] |
| Specific heat of vinyl ester (J/(kg·K)) | 1509 | [17] |
| Initial specific heat of glass/vinyl ester (J/(kg·K)) | 960 | [24] |
| Final specific heat of glass/vinyl ester (J/(kg·K)) | 1360 | [24] |
| Specific heat of gas (vinyl ester) (J/(kg·K)) | 2386.5 | [24] |
| Coefficient of convection (frontal surface) (W/(m2·K)) | 15 | [25] |
| Coefficient of convection (back surface) (W/(m2·K)) | 0 | [25] |
| Radiation source emissivity (-) | 0.8 | [25] |
| Emissivity of the front surface (-) | 0.8 | [25] |
| Emissivity of the back surface (-) | 0.4 | [25] |
| Room temperature (°C) | 20 | [24] |
| Thickness of the sample (m) | 9 × 10−3 | [24] |
| Virgin coefficient of linear thermal expansion (1/K) | 2.52 × 10−5 | [27] |
| Char coefficient of linear thermal expansion (1/K) | 6.3 × 10−5 | [27] |
| Dimensionless expansion factor (-) | −7.778 × 10−2 | [15] |
| Virgin material permeability (m2) | 8.29 × 10−17 | [28] |
| Char material permeability (m2) | 1.56 × 10−10 | [28] |
| Virgin coefficient of permeability (1/K) | 0 | [15] |
| Char coefficient of permeability (1/K) | 0 | [15] |
| Dimensionless permeability factor (-) | −225 | [15] |
| Molecular weight of gases (kg/mol) | 18.35 × 10−3 | [15] |
| Room pressure (normal pressure) (Pa) | 101,325 | – |
| Pressure on the back surface (Pa) | 101,325 | – |
| Gas viscosity (Pa·s) | 1.5 × 10−5 | [15] |
| Property | Value | Source |
|---|---|---|
| Fraction volume of fibers (-) | 0.3 | [25] |
| Kinetics rate constant (1/s) | 1000 | [25] |
| Activation energy (J/mol) | 5 × 104 | [25] |
| Reaction order (-) | 1 | [25] |
| Remaining matrix mass fraction (-) | 0.01 | [25] |
| Heat of decomposition of the matrix (J/kg) | −234,460 | [25] |
| Density of glass fiber (kg/m3) | 2694.7 | [25] |
| Density of polyester (kg/m3) | 1102.4 | [25] |
| Thermal conductivity of glass fiber (W/(m·K)) | 1.04 | [25] |
| Thermal conductivity of polyester (W/(m·K)) | 0.20 | [25] |
| Specific heat of glass fiber (J/(kg·K)) | 760 | [25] |
| Specific heat of polyester (J/(kg·K)) | 1600 | [25] |
| Specific heat of gas (polyester) (J/(kg·K)) | 2386.5 | [24] |
| Coefficient of convection (frontal surface) (W/(m2·K)) | 10 | [25] |
| Coefficient of convection (back surface) (W/(m2·K)) | 0 | [25] |
| Radiation source emissivity (-) | 0.97 | [25] |
| Emissivity of the front surface (-) | 0.8 | [25] |
| Emissivity of the back surface (-) | 0.4 | [25] |
| Room temperature (°C) | 20 | [25] |
| Thickness of the sample (m) | 3.5 × 10−3 | [25] |
| Virgin coefficient of linear thermal expansion (1/K) | 9 × 10−6 | [29] |
| Char coefficient of linear thermal expansion (1/K) | 1.1 × 10−5 | [29] |
| Dimensionless expansion factor (-) | −1 × 10−1 | [15] |
| Virgin material permeability (m2) | 3.19 × 10−16 | [28] |
| Char material permeability (m2) | 1 × 10−10 | [28] |
| Virgin coefficient of permeability (1/K) | 0 | [15] |
| Char coefficient of permeability (1/K) | 0 | [15] |
| Dimensionless permeability factor (-) | −225 | [15] |
| Molecular weight of gases (kg/mol) | 18.35 × 10−3 | [15] |
| Room pressure (normal pressure) (Pa) | 101,325 | – |
| Pressure on the back surface (Pa) | 101,325 | – |
| Gas viscosity (Pa·s) | 1.5 × 10−5 | [15] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Márquez Costa, J.P.; Legrand, V.; Fréour, S. Durability of Composite Materials under Severe Temperature Conditions: Influence of Moisture Content and Prediction of Thermo-Mechanical Properties During a Fire. J. Compos. Sci. 2019, 3, 55. https://doi.org/10.3390/jcs3020055
Márquez Costa JP, Legrand V, Fréour S. Durability of Composite Materials under Severe Temperature Conditions: Influence of Moisture Content and Prediction of Thermo-Mechanical Properties During a Fire. Journal of Composites Science. 2019; 3(2):55. https://doi.org/10.3390/jcs3020055
Chicago/Turabian StyleMárquez Costa, Juan Pablo, Vincent Legrand, and Sylvain Fréour. 2019. "Durability of Composite Materials under Severe Temperature Conditions: Influence of Moisture Content and Prediction of Thermo-Mechanical Properties During a Fire" Journal of Composites Science 3, no. 2: 55. https://doi.org/10.3390/jcs3020055





