Numerical Model for a Geometrically Nonlinear Analysis of Beams with Composite Cross-Sections
Abstract
:1. Introduction
2. Kinematics of the Beam Element
3. Cross-Section Properties
4. Governing Equations
5. Finite Element Formulation
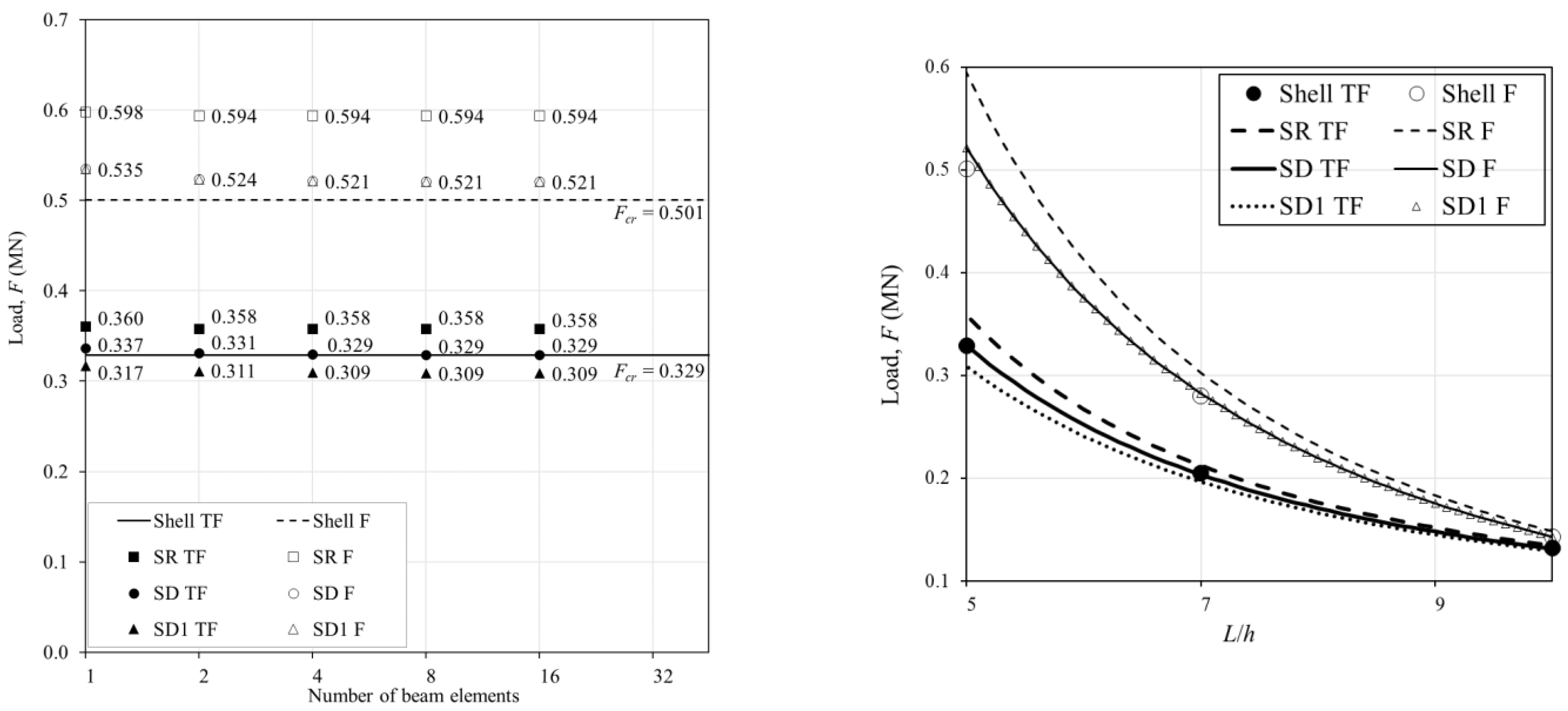
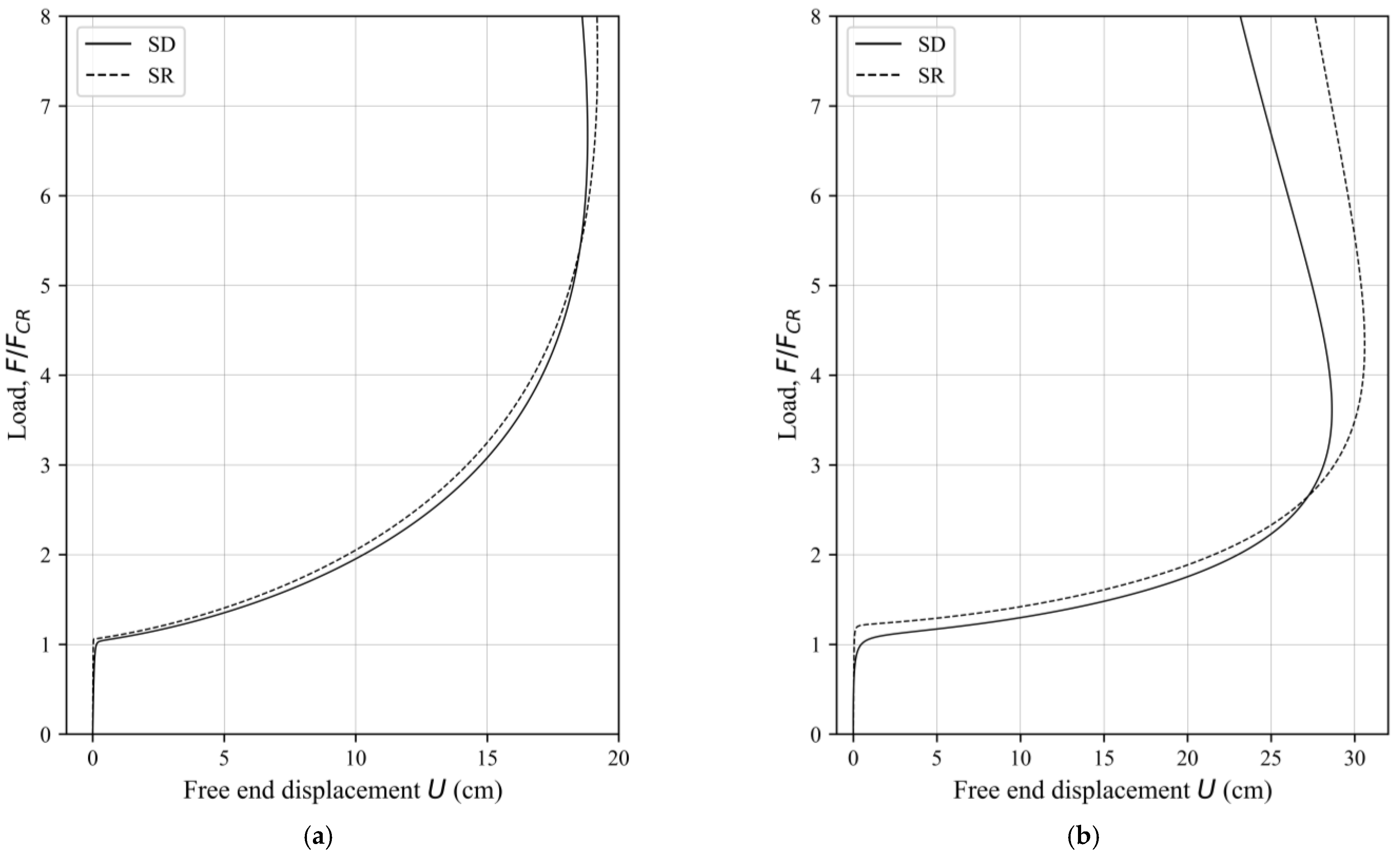
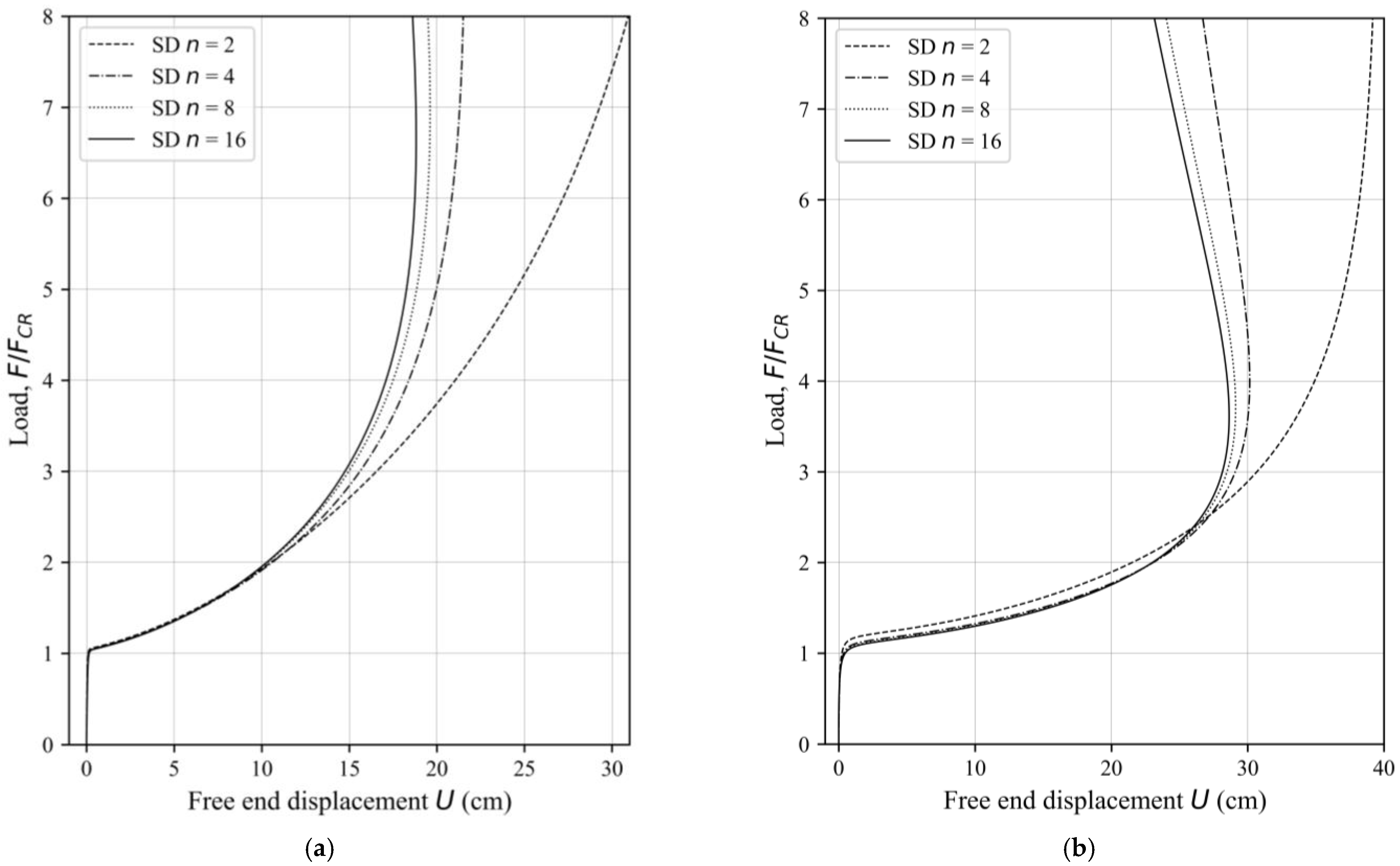
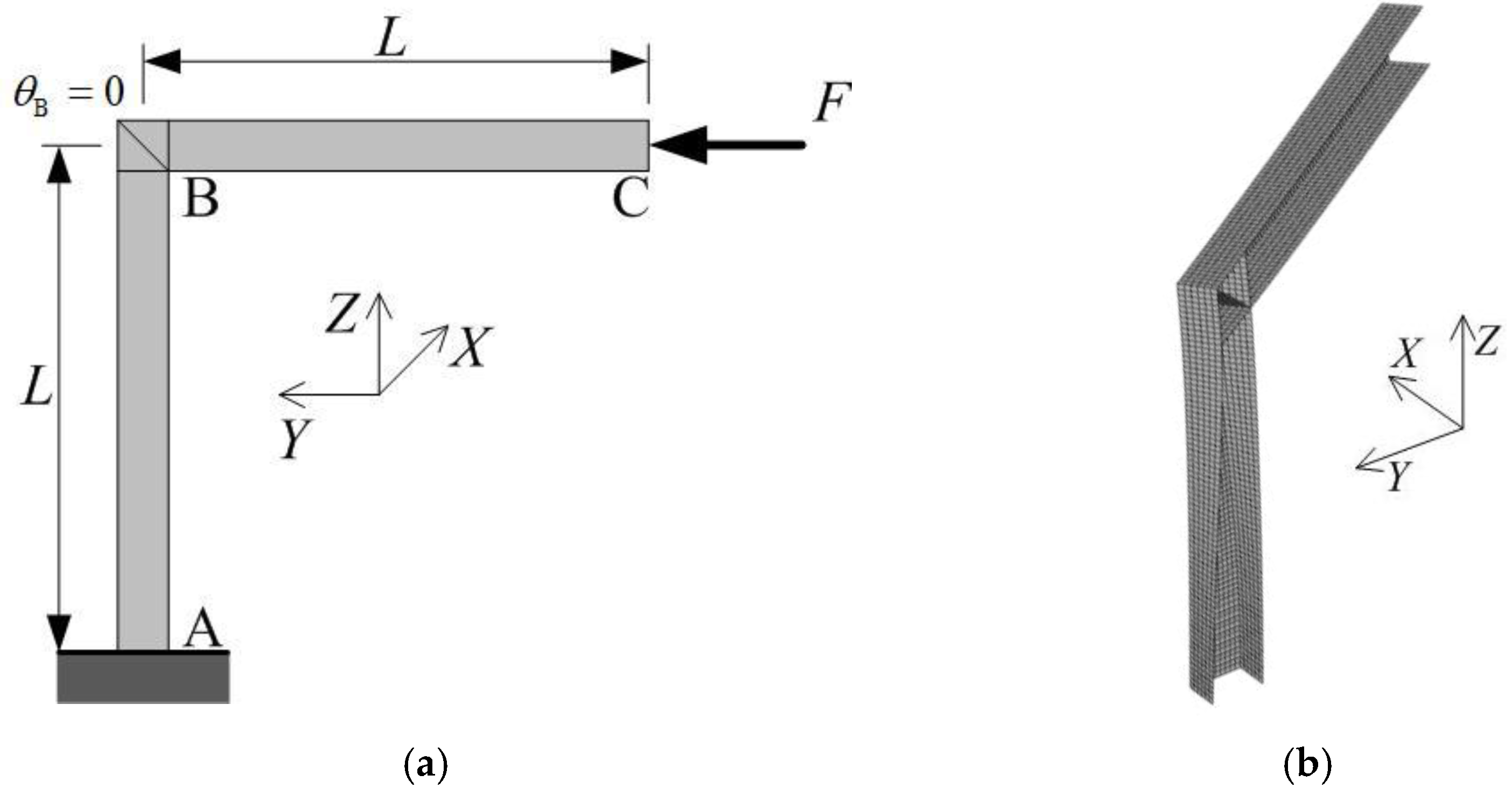
6. Numerical Examples
6.1. Example 1
6.2. Example 2
6.3. Example 3
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Kollár, L.P.; Springer, G.S. Mechanics of Composite Structures, 1st ed.; Cambridge University Press: New York, NY, USA, 2003; ISBN 978-0-521-12690-8. [Google Scholar]
- Librescu, L.; Song, O. Thin-Walled Composite Beams: Theory and Applications, 1st ed.; Springer: Berlin, Germany, 2006; ISBN 978-1-4020-3457-2. [Google Scholar]
- Vasiliev, V.V.; Morozov, E.V. Advanced Mechanics of Composite Materials and Structural Elements, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2013; ISBN 978-0-08-098231-1. [Google Scholar]
- Bakis, C.E.; Bank, L.C.; Brown, V.L.; Cosenza, E.; Davalos, J.F.; Lesko, J.J.; Machida, A.; Rizkalla, S.H.; Triantafillou, T.C. Fiber-Reinforced Polymer Composites for Construction-State-of-the-Art Review. J. Compos. Constr. 2003, 6, 369–383. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.L.; Zhang, L. State-of-the-Art Review on FRP Strengthened Steel Structures. Eng. Struct. 2007, 29, 1808–1823. [Google Scholar] [CrossRef]
- Vedernikov, A.; Gemi, L.; Madenci, E.; Özkılıç, Y.O.; Yazman, Ş.; Gusev, S.; Sulimov, A.; Bondareva, J.; Evlashina, S.; Konev, S.; et al. Effects of High Pulling Speeds on Mechanical Properties and Morphology of Pultruded GFRP Composite Flat Laminates. Compos. Struct. 2022, 301, 116216. [Google Scholar] [CrossRef]
- Vedernikov, A.; Minchenkov, K.; Gusev, S.; Sulimov, A.; Zhou, P.; Li, C.; Xian, G.; Akhatov, I.; Safonov, A. Effects of the Pre-Consolidated Materials Manufacturing Method on the Mechanical Properties of Pultruded Thermoplastic Composites. Polymers 2022, 14, 2246. [Google Scholar] [CrossRef] [PubMed]
- Hamed, M.A.; Abo-bakr, R.M.; Mohamed, S.A.; Eltaher, M.A. Influence of Axial Load Function and Optimization on Static Stability of Sandwich Functionally Graded Beams with Porous Core. Eng. Comput. 2020, 36, 1929–1946. [Google Scholar] [CrossRef]
- Mohamed, N.; Mohamed, S.A.; Eltaher, M.A. Buckling and Post-Buckling Behaviors of Higher Order Carbon Nanotubes Using Energy-Equivalent Model. Eng. Comput. 2021, 37, 2823–2836. [Google Scholar] [CrossRef]
- Carrera, E.; Filippi, M.; Mahato, P.K.; Pagani, A. Accurate Static Response of Single- and Multi-Cell Laminated Box Beams. Compos. Struct. 2016, 136, 372–383. [Google Scholar] [CrossRef] [Green Version]
- Pagani, A.; Carrera, E. Unified Formulation of Geometrically Nonlinear Refined Beam Theories. Mech. Adv. Mater. Struct. 2018, 25, 15–31. [Google Scholar] [CrossRef] [Green Version]
- Bebiano, R.; Camotim, D.; Gonçalves, R. GBTUL 2.0−A Second-Generation Code for the GBT-Based Buckling and Vibration Analysis of Thin-Walled Members. Thin-Walled Struct. 2018, 124, 235–257. [Google Scholar] [CrossRef]
- Cortínez, V.H.; Piovan, M.T. Vibration and Buckling of Composite Thin-Walled Beams with Shear Deformability. J. Sound Vib. 2002, 258, 701–723. [Google Scholar] [CrossRef]
- Reddy, J.N. Microstructure-Dependent Couple Stress Theories of Functionally Graded Beams. J. Mech. Phys. Solids 2011, 59, 2382–2399. [Google Scholar] [CrossRef]
- Thai, H.T. A Nonlocal Beam Theory for Bending, Buckling, and Vibration of Nanobeams. Int. J. Eng. Sci. 2012, 52, 56–64. [Google Scholar] [CrossRef]
- Gjelsvik, A. The Theory of Thin Walled Bars; Wiley: New York, NY, USA, 1981. [Google Scholar]
- Turkalj, G.; Brnic, J.; Lanc, D.; Kravanja, S. Updated Lagrangian Formulation for Nonlinear Stability Analysis of Thin-Walled Frames with Semi-Rigid Connections. Int. J. Struct. Stab. Dyn. 2012, 12, 1250013. [Google Scholar] [CrossRef]
- Carrera, E.; Giunta, G.; Nali, P.; Petrolo, M. Refined Beam Elements with Arbitrary Cross-Section Geometries. Comput. Struct. 2010, 88, 283–293. [Google Scholar] [CrossRef]
- Tang, H.; Li, L.; Hu, Y.; Meng, W.; Duan, K. Vibration of Nonlocal Strain Gradient Beams Incorporating Poisson’s Ratio and Thickness Effects. Thin-Walled Struct. 2019, 137, 377–391. [Google Scholar] [CrossRef]
- Hadji, L.; Avcar, M. Nonlocal Free Vibration Analysis of Porous FG Nanobeams Using Hyperbolic Shear Deformation Beam Theory. Adv. Nano Res. 2021, 10, 281–293. [Google Scholar]
- Kim, N., II; Lee, B.J.; Kim, M.Y. Exact Element Static Stiffness Matrices of Shear Deformable Thin-Walled Beam-Columns. Thin-Walled Struct. 2004, 42, 1231–1256. [Google Scholar] [CrossRef]
- Kim, N., II; Kim, M.Y. Exact Dynamic/Static Stiffness Matrices of Non-Symmetric Thin-Walled Beams Considering Coupled Shear Deformation Effects. Thin-Walled Struct. 2005, 43, 701–734. [Google Scholar] [CrossRef]
- Minghini, F.; Tullini, N.; Laudiero, F. Buckling Analysis of FRP Pultruded Frames Using Locking-Free Finite Elements. Thin-Walled Struct. 2008, 46, 223–241. [Google Scholar] [CrossRef]
- Minghini, F.; Tullini, N.; Laudiero, F. Elastic Buckling Analysis of Pultruded FRP Portal Frames Having Semi-Rigid Connections. Eng. Struct. 2009, 31, 292–299. [Google Scholar] [CrossRef]
- Turkalj, G.; Lanc, D.; Banić, D.; Brnić, J.; Vo, T.P. A Shear-Deformable Beam Model for Stability Analysis of Orthotropic Composite Semi-Rigid Frames. Compos. Struct. 2018, 189, 648–660. [Google Scholar] [CrossRef]
- Pilkey, W.D. Analysis and Design of Elastic Beams: Computational Methods; Wiley: New York, NY, USA, 2002; ISBN 0471381527. [Google Scholar]
- Banić, D.; Turkalj, G.; Lanc, D. Stability Analysis of Shear Deformable Cross-Ply Laminated Composite Beam-Type Structures. Compos. Struct. 2023, 303, 116270. [Google Scholar] [CrossRef]
- Minghini, F.; Tullini, N.; Laudiero, F. Locking-Free Finite Elements for Shear Deformable Orthotropic Thin-Walled Beams. Int. J. Numer. Meth. Engng 2007, 72, 808–834. [Google Scholar] [CrossRef]
- Lanc, D.; Vo, T.P.; Turkalj, G.; Lee, J. Buckling Analysis of Thin-Walled Functionally Graded Sandwich Box Beams. Thin-Walled Struct. 2015, 86, 148–156. [Google Scholar] [CrossRef] [Green Version]
- Lanc, D.; Turkalj, G.; Vo, T.P.; Brnić, J. Nonlinear Buckling Behaviours of Thin-Walled Functionally Graded Open Section Beams. Compos. Struct. 2016, 152, 829–839. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Kuo, S. Theory and Analysis of Nonlinear Framed Structures; Prentice Hall: Hoboken, NJ, USA, 1994. [Google Scholar]
- Reddy, J.N. Energy Principles and Variational Methods in Applied Mechanics. In Theory and Analysis of Elastic Plates and Shells; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Argyris, J.H.; Dunne, P.C.; Malejannakis, G.; Scharpf, D.W. On Large Displacement-Small Strain Analysis of Flexibly Connected Thin-Walled Beam-Type Structures. Comput. Methods Appl. Mech. Eng. 1978, 15, 99–135. [Google Scholar] [CrossRef]
- Turkalj, G.; Lanc, D.; Pesic, I. A Beam Formulation for Large Displacement Analysis of Composite Frames with Semi-Rigid Connections. Compos. Struct. 2015, 134, 237–246. [Google Scholar] [CrossRef]
- Turkalj, G.; Brnic, J.; Kravanja, S. A Beam Model for Large Displacement Analysis of Flexibly Connected Thin-Walled Beam-Type Structures. Thin-Walled Struct. 2011, 49, 1007–1016. [Google Scholar] [CrossRef]
- Lee, J.; Kim, S.E.; Hong, K. Lateral Buckling of I-Section Composite Beams. Eng. Struct. 2002, 24, 955–964. [Google Scholar] [CrossRef]
- Lee, J. Flexural Analysis of Thin-Walled Composite Beams Using Shear-Deformable Beam Theory. Compos. Struct. 2005, 70, 212–222. [Google Scholar] [CrossRef]
- Chen, W.-F.; Atsuta, T. Theory of Beam Columns; J. Ross Publishing: New York, NY, USA, 2008; Volume 2, ISBN 978-1-932159-77-6. [Google Scholar]
- McGuire, W.; Gallagher, R.H.; Ziemian, R.D. Matrix Structural Analysis, 2nd ed.; Wiley: New York, NY, USA, 1999. [Google Scholar]




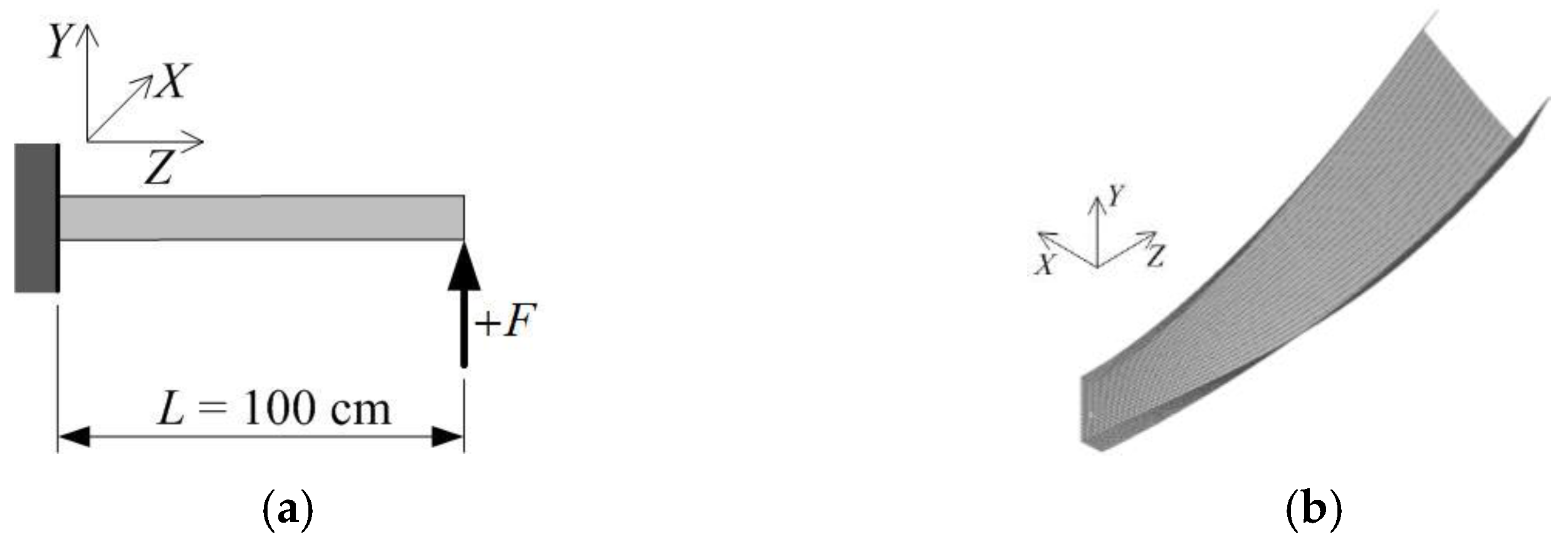

| [0°/90°/0°] | (cm2) | (cm4) | (cm4) | (cm4) | (cm4) | xc (cm) | xg (cm) | xs (cm) |
| 22 | 532.343 | 72.525 | 7.333 | 1718.819 | 3.159 | 4.364 | 5.767 | |
| Kx | Ky | Kω | Kyω | (GPa) | (GPa) | |||
| 2.1504 | 2.3969 | 0.0217 | −0.4999 | 82.932 | 4.14 |
| [0°/90°/0°] | (cm2) | (cm4) | (cm4) | (cm4) | (cm4) | xs (cm) | ys (cm) | α (°) |
| 16 | 342.486 | 17.701 | 5.333 | 186.781 | 2.782 | −1.769 | 6.404 | |
| (GPa) | (GPa) | Kx | Ky | Kω | Kxy | Kxω | Kyω | |
| 60.031 | 4.14 | 3.2748 | 1.6373 | 0.0358 | −36.7315 | −1.2571 | −0.7571 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banić, D.; Turkalj, G.; Kvaternik Simonetti, S.; Lanc, D. Numerical Model for a Geometrically Nonlinear Analysis of Beams with Composite Cross-Sections. J. Compos. Sci. 2022, 6, 377. https://doi.org/10.3390/jcs6120377
Banić D, Turkalj G, Kvaternik Simonetti S, Lanc D. Numerical Model for a Geometrically Nonlinear Analysis of Beams with Composite Cross-Sections. Journal of Composites Science. 2022; 6(12):377. https://doi.org/10.3390/jcs6120377
Chicago/Turabian StyleBanić, Damjan, Goran Turkalj, Sandra Kvaternik Simonetti, and Domagoj Lanc. 2022. "Numerical Model for a Geometrically Nonlinear Analysis of Beams with Composite Cross-Sections" Journal of Composites Science 6, no. 12: 377. https://doi.org/10.3390/jcs6120377





