Analysis of Intact/Delaminated Composite and Sandwich Beams Using a Higher-Order Modeling Technique
Abstract
:1. Introduction
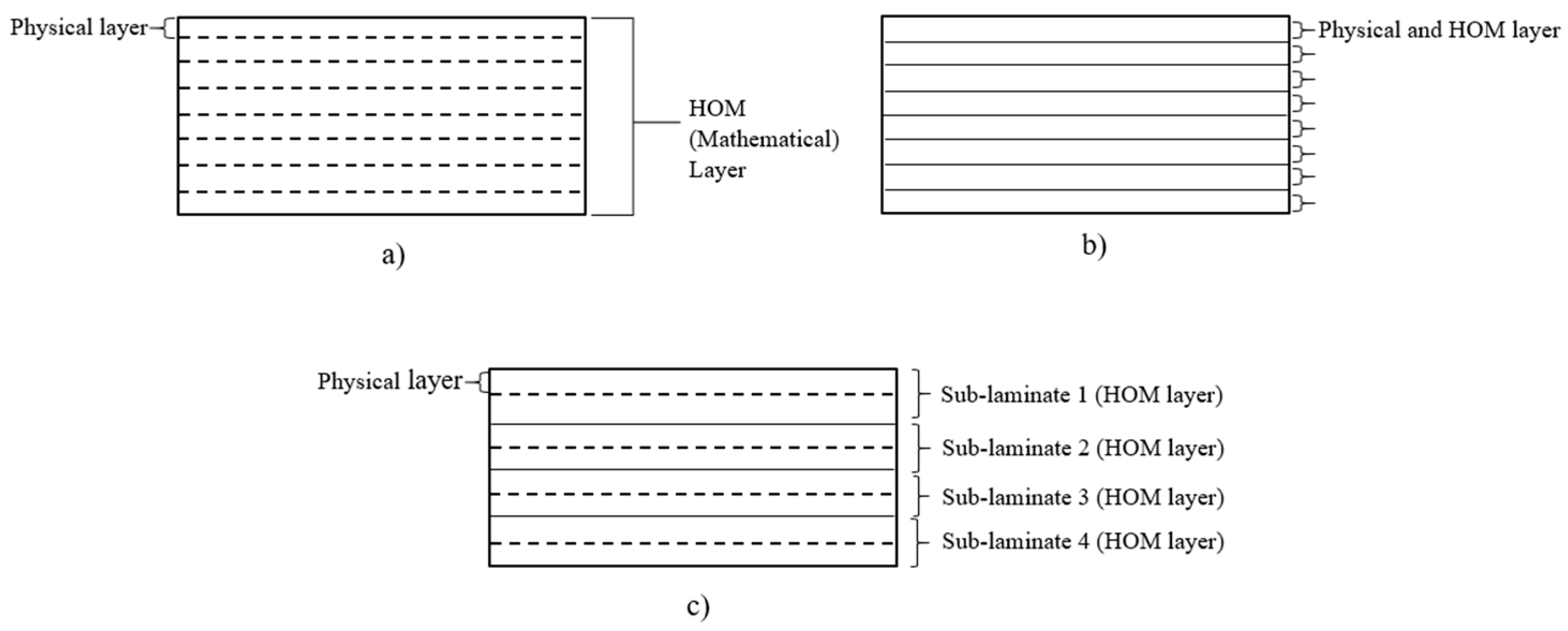
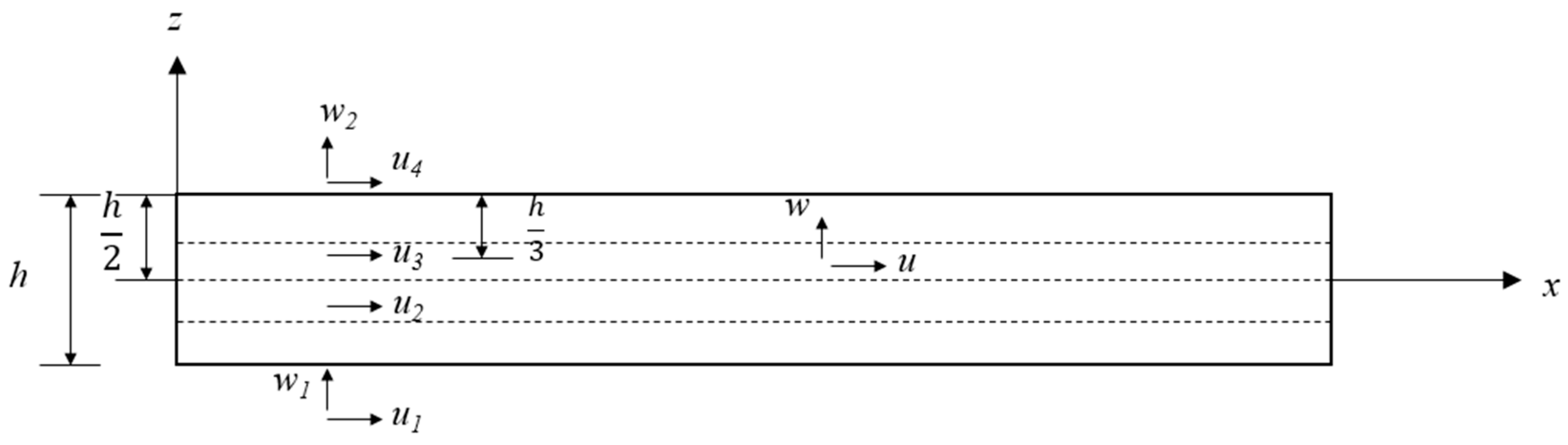
2. Mathematical Formulations
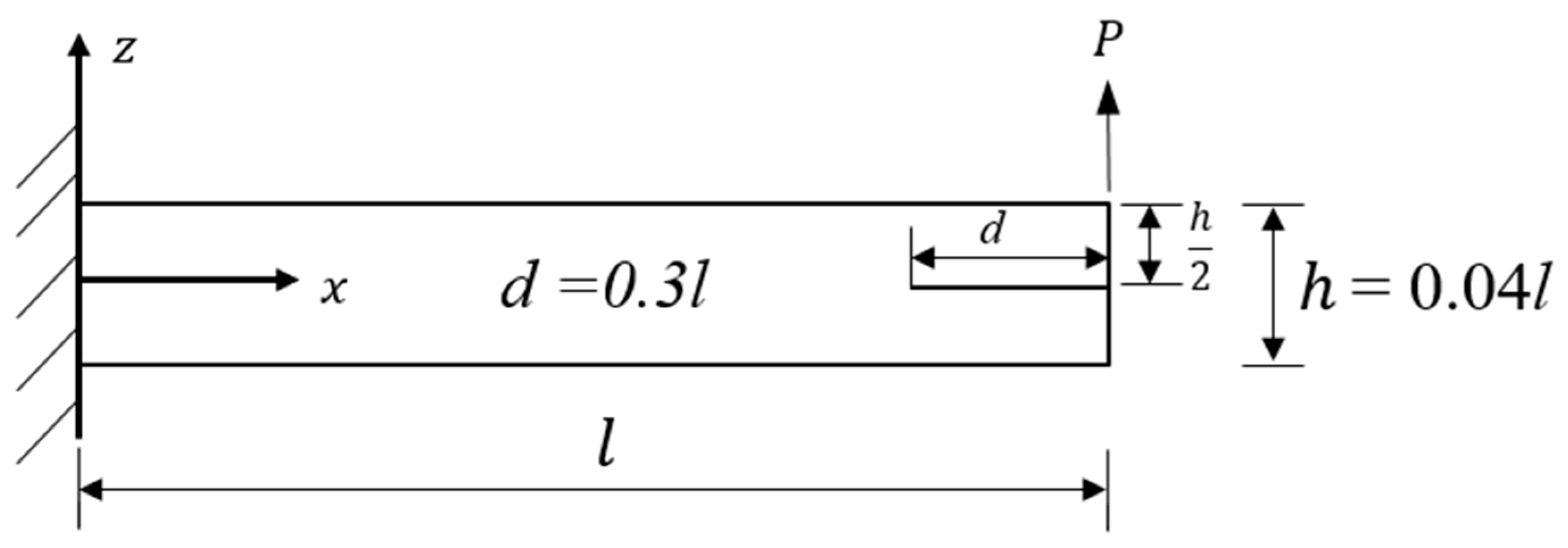
3. Numerical Examples for Validation
3.1. Intact Laminated Composite Beams
3.2. Intact Laminated Sandwich Beams
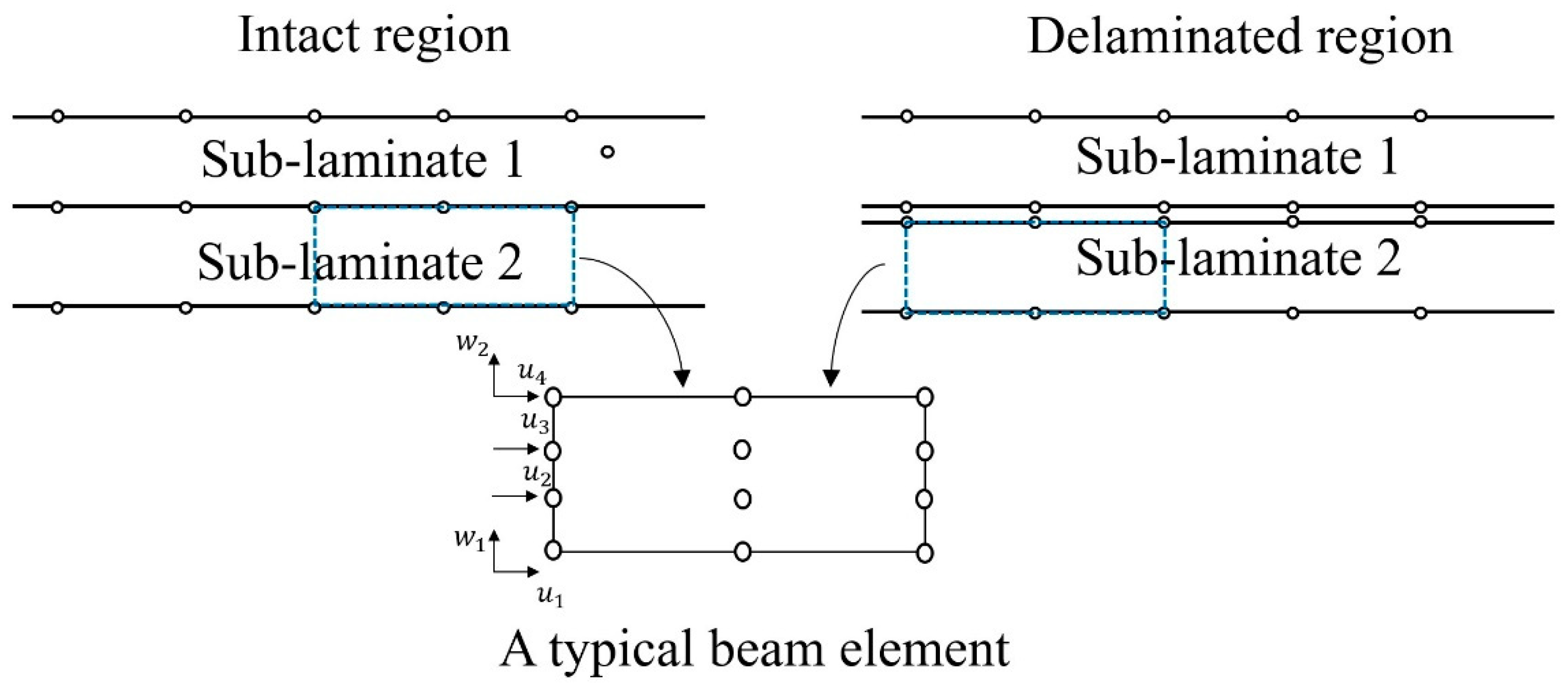
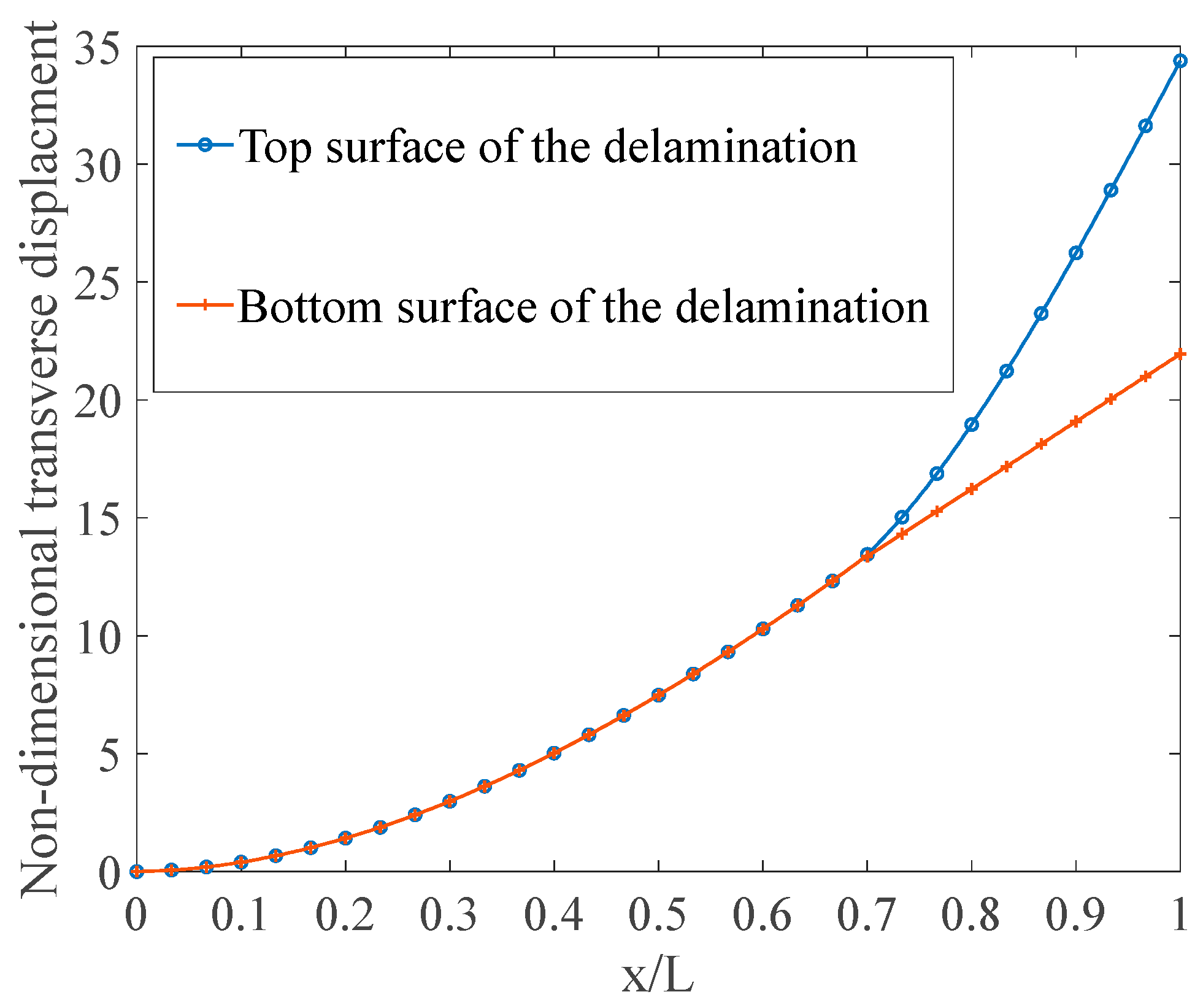
3.3. Laminated Composite Beam Contating Delamiantion
4. Conclusions
- The present model shows encouraging performance in analyzing multilayered structures subjected to different types of static loading. The incorporation of transverse displacement variation was beneficial in modeling the sandwich beams, especially subjected to localized load (e.g., point load). The proposed model also showed a good estimation for transverse shear stresses, which were calculated directly from the constitutive relationship. Moreover, modeling the whole structure with a single sub-laminate showed a better performance than the typical higher-order model with the equivalent single-layer hypothesis.
- The model provides ease in the simulation of delamination by inserting it between two sub-laminates. The numerical results also showed that the model has adequate accuracy in analyzing delaminated composite beams.
- The HOM-based model has high flexibility to choose the level of detail in the variation of displacement through the thickness for the modeling of multilayer composite and sandwich beams with or without delamination by choosing an appropriate sub-lamination scheme. Therefore, users can balance computational efficiency and prediction accuracy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Doughett, A.; Asnarez, P. Composite Laminates: Properties, Performance and Applications; Nova Science Publishers, Incorporated: Hauppauge, NY, USA, 2010. [Google Scholar]
- Reddy, J. An evaluation of equivalent-single-layer and layerwise theories of composite laminates. Compos. Struct. 1993, 25, 21–35. [Google Scholar] [CrossRef]
- Kreja, I. A literature review on computational models for laminated composite and sandwich panels. Open Eng. 2011, 1, 59–80. [Google Scholar] [CrossRef]
- Maji, A.; Mahato, P.K. Development and applications of shear deformation theories for laminated composite plates: An overview. J. Thermoplast. Compos. Mater. 2022, 35, 2576–2619. [Google Scholar] [CrossRef]
- Li, D. Layerwise theories of laminated composite structures and their applications: A review. Arch. Comput. Methods Eng. 2021, 28, 577–600. [Google Scholar] [CrossRef]
- Fan, H.; Widera, G. Refined engineering beam theory based on the asymptotic expansion approach. AIAA J. 1991, 29, 444–449. [Google Scholar] [CrossRef]
- Mechab, I.; Tounsi, A.; Benatta, M. Deformation of short composite beam using refined theories. J. Math. Anal. Appl. 2008, 346, 468–479. [Google Scholar] [CrossRef]
- Thai, H.-T.; Choi, D.-H. A simple first-order shear deformation theory for laminated composite plates. Compos. Struct. 2013, 106, 754–763. [Google Scholar] [CrossRef]
- Amir, S.; Khorasani, M.; BabaAkbar-Zarei, H. Buckling analysis of nanocomposite sandwich plates with piezoelectric face sheets based on flexoelectricity and first-order shear deformation theory. J. Sandw. Struct. Mater. 2020, 22, 2186–2209. [Google Scholar] [CrossRef]
- Whitney, J.; Sun, C. A higher order theory for extensional motion of laminated composites. J. Sound Vib. 1973, 30, 85–97. [Google Scholar] [CrossRef]
- Reddy, J.N. A Simple Higher-Order Theory for Laminated Composite Plates. J. Appl. Mech. 1984, 51, 745–752. [Google Scholar] [CrossRef]
- Matsunaga, H. Interlaminar stress analysis of laminated composite beams according to global higher-order deformation theories. Compos. Struct. 2002, 55, 105–114. [Google Scholar] [CrossRef]
- Vidal, P.; Polit, O. A family of sinus finite elements for the analysis of rectangular laminated beams. Compos. Struct. 2008, 84, 56–72. [Google Scholar] [CrossRef]
- Pawar, E.G.; Banerjee, S.; Desai, Y.M. Stress analysis of laminated composite and sandwich beams using a novel shear and normal deformation theory. Lat. Am. J. Solids Struct. 2015, 12, 1340–1361. [Google Scholar] [CrossRef]
- Sayyad, A.S.; Ghugal, Y.M. Static and free vibration analysis of laminated composite and sandwich spherical shells using a generalized higher-order shell theory. Compos. Struct. 2019, 219, 129–146. [Google Scholar] [CrossRef]
- Whitney, J.M. Shear Correction Factors for Orthotropic Laminates under Static Load. J. Appl. Mech. 1973, 40, 302–304. [Google Scholar] [CrossRef]
- Reddy, J. A generalization of two-dimensional theories of laminated composite plates. Commun. Appl. Numer. Methods 1987, 3, 173–180. [Google Scholar] [CrossRef]
- Shimpi, R.; Ghugal, Y. A layerwise trigonometric shear deformation theory for two layered cross-ply laminated beams. J. Reinf. Plast. Compos. 1999, 18, 1516–1543. [Google Scholar] [CrossRef]
- Setoodeh, A.R.; Karami, G. Static, free vibration and buckling analysis of anisotropic thick laminated composite plates on distributed and point elastic supports using a 3-D layer-wise FEM. Eng. Struct. 2004, 26, 211–220. [Google Scholar] [CrossRef]
- Afshin, M.; Taheri-Behrooz, F. Interlaminar stresses of laminated composite beams resting on elastic foundation subjected to transverse loading. Comput. Mater. Sci. 2015, 96, 439–447. [Google Scholar] [CrossRef]
- Van Do, V.N.; Lee, C.-H. Isogeometric layerwise formulation for bending and free vibration analysis of laminated composite plates. Acta Mech. 2021, 232, 1329–1351. [Google Scholar] [CrossRef]
- Averill, R.C. Static and dynamic response of moderately thick laminated beams with damage. Compos. Eng. 1994, 4, 381–395. [Google Scholar] [CrossRef]
- Kapuria, S.; Dumir, P.; Ahmed, A. An efficient higher order zigzag theory for composite and sandwich beams subjected to thermal loading. Int. J. Solids Struct. 2003, 40, 6613–6631. [Google Scholar] [CrossRef]
- Vidal, P.; Polit, O. A sine finite element using a zig-zag function for the analysis of laminated composite beams. Compos. Part B Eng. 2011, 42, 1671–1682. [Google Scholar] [CrossRef]
- Nallim, L.G.; Oller, S.; Oñate, E.; Flores, F.G. A hierarchical finite element for composite laminated beams using a refined zigzag theory. Compos. Struct. 2017, 163, 168–184. [Google Scholar] [CrossRef]
- Abrate, S.; Di Sciuva, M. 1.16 Multilayer Models for Composite and Sandwich Structures. In Comprehensive Composite Materials II; Beaumont, P.W.R., Zweben, C.H., Eds.; Elsevier: Oxford, UK, 2018; pp. 399–425. [Google Scholar]
- Dorduncu, M. Stress analysis of laminated composite beams using refined zigzag theory and peridynamic differential operator. Compos. Struct. 2019, 218, 193–203. [Google Scholar] [CrossRef]
- Chakrabarti, A.; Sheikh, A. Vibration of laminate-faced sandwich plate by a new refined element. J. Aerosp. Eng. 2004, 17, 123–134. [Google Scholar] [CrossRef]
- Chakrabarti, A.; Sheikh, A. Behavior of laminated sandwich plates having interfacial imperfections by a new refined element. Comput. Mech. 2004, 34, 87–98. [Google Scholar] [CrossRef]
- Tessler, A.; Di Sciuva, M.; Gherlone, M. Refinement of Timoshenko Beam Theory for Composite and Sandwich Beams Using Zigzag Kinematics; NASA Technical Reports Server (NTRS): Washington, DC, USA, 2007. [Google Scholar]
- Pandit, M.K.; Sheikh, A.H.; Singh, B.N. An improved higher order zigzag theory for the static analysis of laminated sandwich plate with soft core. Finite Elem. Anal. Des. 2008, 44, 602–610. [Google Scholar] [CrossRef]
- Chakrabarti, A.; Chalak, H.; Iqbal, M.A.; Sheikh, A.H. A new FE model based on higher order zigzag theory for the analysis of laminated sandwich beam with soft core. Compos. Struct. 2011, 93, 271–279. [Google Scholar] [CrossRef]
- Chalak, H.D.; Chakrabarti, A.; Iqbal, M.A.; Hamid Sheikh, A. An improved C0 FE model for the analysis of laminated sandwich plate with soft core. Finite Elem. Anal. Des. 2012, 56, 20–31. [Google Scholar] [CrossRef]
- Chalak, H.D.; Chakrabarti, A.; Sheikh, A.H.; Iqbal, M.A. C0 FE model based on HOZT for the analysis of laminated soft core skew sandwich plates: Bending and vibration. Appl. Math. Model. 2014, 38, 1211–1223. [Google Scholar] [CrossRef]
- Soldatos, K.; Timarci, T. A unified formulation of laminated composite, shear deformable, five-degrees-of-freedom cylindrical shell theories. Compos. Struct. 1993, 25, 165–171. [Google Scholar] [CrossRef]
- Carrera, E. Theories and finite elements for multilayered plates and shells: A unified compact formulation with numerical assessment and benchmarking. Arch. Comput. Methods Eng. 2003, 10, 215–296. [Google Scholar] [CrossRef]
- Demasi, L. ∞3 Hierarchy plate theories for thick and thin composite plates: The generalized unified formulation. Compos. Struct. 2008, 84, 256–270. [Google Scholar] [CrossRef]
- Ferreira, A.; Araújo, A.; Neves, A.; Rodrigues, J.; Carrera, E.; Cinefra, M.; Soares, C.M. A finite element model using a unified formulation for the analysis of viscoelastic sandwich laminates. Compos. Part B Eng. 2013, 45, 1258–1264. [Google Scholar] [CrossRef]
- Bharati, R.B.; Filippi, M.; Mahato, P.K.; Carrera, E. Flutter analysis of laminated composite structures using Carrera Unified Formulation. Compos. Struct. 2020, 253, 112759. [Google Scholar] [CrossRef]
- Lee, J.; Gurdal, Z.; Griffin, O.H., Jr. Layer-wise approach for the bifurcation problem in laminated composites with delaminations. AIAA J. 1993, 31, 331–338. [Google Scholar] [CrossRef]
- Na, W.J.; Reddy, J. Delamination in cross-ply laminated beams using the layerwise theory. Asian J. Civ. Eng. Build. Hous. 2009, 10, 451–480. [Google Scholar]
- Chrysochoidis, N.; Saravanos, D. Layerwise dynamic response models for delamination composite beams with active piezoelectric sensors. In Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Austin, TX, USA, 18–21 April 2005; p. 2186. [Google Scholar]
- Kharghani, N.; Guedes Soares, C. Influence of different parameters on the deflection of composite laminates containing through-the-width delamination using Layerwise HSDT. Compos. Struct. 2015, 132, 341–349. [Google Scholar] [CrossRef]
- Siorikis, D.; Rekatsinas, C.; Chrysochoidis, N.; Saravanos, D. An extended layerwise spectral finite element framework for delamination growth simulation in laminated composite strips. Compos. Struct. 2021, 276, 114452. [Google Scholar] [CrossRef]
- Cho, Y.; Averill, R. First-order zig-zag sublaminate plate theory and finite element model for laminated composite and sandwich panels. Compos. Struct. 2000, 50, 1–15. [Google Scholar] [CrossRef]
- Pai, P.F.; Palazotto, A.N. Two-dimensional sublamination theory for analysis of functionally graded plates. J. Sound Vib. 2007, 308, 164–189. [Google Scholar]
- Williams, T.O. A new, unified, theoretical framework for the formulation of general, nonlinear, single-scale shell theories. Compos. Struct. 2014, 107, 544–558. [Google Scholar] [CrossRef]
- d’Ottavio, M.; Dozio, L.; Vescovini, R.; Polit, O. Bending analysis of composite laminated and sandwich structures using sublaminate variable-kinematic Ritz models. Compos. Struct. 2016, 155, 45–62. [Google Scholar] [CrossRef]
- Pagano, N. Exact solutions for composite laminates in cylindrical bending. J. Compos. Mater. 1969, 3, 398–411. [Google Scholar] [CrossRef]
- Fish, J.; Belytschko, T. A First Course in Finite Elements; John Wiley & Sons: Hoboken, NJ, USA, 2007; Volume 1. [Google Scholar]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]

| Lamination Scheme | Source | S = 5 | % Error 1 | S = 20 | % Error | S = 50 | % Error |
|---|---|---|---|---|---|---|---|
| 0/90/90/0 | Present (NS1) | 2.2949 | 3.94 | 0.6710 | 1.44 | 0.5764 | 0.52 |
| Present (NS2) | 2.3103 | 3.29 | 0.6744 | 0.94 | 0.5780 | 0.24 | |
| Present (NS4) | 2.3884 | 0.03 | 0.6807 | 0.01 | 0.5793 | 0.02 | |
| Reddy [11] | 2.2764 | 4.71 | 0.6699 | 1.60 | 0.5776 | 0.31 | |
| Pagano [49] | 2.3890 | 0.6808 | 0.5794 | ||||
| 0/90/0/90 | Present (NS1) | 2.7298 | 13.47 | 1.2237 | 3.17 | 1.1376 | 1.04 |
| Present (NS2) | 3.0762 | 2.49 | 1.2562 | 0.59 | 1.1470 | 0.23 | |
| Present (NS4) | 3.1535 | 0.04 | 1.2633 | 0.03 | 1.1492 | 0.03 | |
| Reddy [11] | 2.5588 | 18.89 | 1.2184 | 3.58 | 1.1423 | 0.64 | |
| Pagano [49] | 3.1547 | 1.2637 | 1.1496 |
| S | Source | % Error | % Error | ||
|---|---|---|---|---|---|
| 5 | Present (NS1) | 26.54 | 1.23 | 1.819 | 3.55 |
| Present (NS2) | 26.43 | 1.64 | 2.251 | 19.35 | |
| Present (NS4) | 26.81 | 0.22 | 1.896 | 0.35 | |
| Reddy [11] | 24.94 | 7.18 | 1.729 | 8.32 | |
| Pagano [49] | 26.87 | 1.886 | 3.55 | ||
| 20 | Present (NS1) | 285.6 | 0.45 | 7.704 | 5.72 |
| Present (NS2) | 285.8 | 0.38 | 9.848 | 20.52 | |
| Present (NS4) | 286.3 | 0.21 | 8.215 | 0.54 | |
| Reddy [11] | 284.2 | 0.94 | 7.089 | 13.13 | |
| Pagano [49] | 286.9 | 8.171 | |||
| 50 | Present (NS1) | 1732.2 | 0.32 | 19.52 | 4.92 |
| Present (NS2) | 1733.7 | 0.23 | 24.94 | 21.48 | |
| Present (NS4) | 1734.2 | 0.20 | 20.83 | 1.46 | |
| Reddy [11] | 1735.0 | 0.16 | 17.75 | 13.54 | |
| Pagano [49] | 1737.7 | 20.53 | 4.92 |
| S | Source | Beam Bottom | % Error | Beam Top | % Error | Mid-Plane | % Error |
|---|---|---|---|---|---|---|---|
| (a) | |||||||
| 5 | Pagano [49] | 15.653 | 23.395 | 17.138 | 16.3 | ||
| Reddy [11] | 14.345 | 8.36 | 14.345 | 38.68 | 14.345 | 0.51 | |
| Present (NS1) | 15.663 | 0.06 | 18.788 | 19.69 | 17.225 | 2.40 | |
| Present (NS4) | 15.475 | 1.14 | 23.318 | 0.33 | 16.726 | 2.44 | |
| Present (NS6) | 15.502 | 0.96 | 23.592 | 0.84 | 17.720 | 16.3 | |
| 20 | Pagano [49] | 3.7467 | 3.8525 | 3.7717 | |||
| Reddy [11] | 3.4464 | 8.02 | 3.4464 | 10.5 | 3.4464 | 8.62 | |
| Present (NS1) | 3.7202 | 0.71 | 3.7690 | 2.17 | 3.7446 | 0.72 | |
| Present (NS4) | 3.7432 | 0.09 | 3.8627 | 0.26 | 3.7639 | 0.21 | |
| Present (NS6) | 3.7446 | 0.06 | 3.8655 | 0.34 | 3.7651 | 0.17 | |
| 50 | Pagano [49] | 2.9281 | 2.9331 | 2.9297 | |||
| Reddy [11] | 2.8157 | 3.84 | 2.8157 | 4.00 | 2.8157 | 3.89 | |
| Present (NS1) | 2.9149 | 0.45 | 2.9179 | 0.52 | 2.9164 | 0.45 | |
| Present (NS4) | 2.9276 | 0.02 | 2.9350 | 0.06 | 2.9292 | 0.02 | |
| Present (NS6) | 2.9279 | 0.01 | 2.9353 | 0.08 | 2.9295 | 0.01 | |
| (b) | |||||||
| 5 | Pagano [49] | 15.653 | 23.395 | 17.138 | |||
| Reddy [11] | 14.345 | 8.36 | 14.345 | 38.68 | 14.345 | 16.3 | |
| Present (NS1) | 15.663 | 0.06 | 18.788 | 19.69 | 17.225 | 0.51 | |
| Present (NS4) | 15.475 | 1.14 | 23.318 | 0.33 | 16.726 | 2.40 | |
| Present (NS6) | 15.502 | 0.96 | 23.592 | 0.84 | 16.720 | 2.44 | |
| 20 | Pagano [49] | 3.7467 | 3.8525 | 3.7717 | |||
| Reddy [11] | 3.4464 | 8.02 | 3.4464 | 10.5 | 3.4464 | 8.62 | |
| Present (NS1) | 3.7202 | 0.71 | 3.7690 | 2.17 | 3.7446 | 0.72 | |
| Present (NS4) | 3.7432 | 0.09 | 3.8627 | 0.26 | 3.7639 | 0.21 | |
| Present (NS6) | 3.7446 | 0.06 | 3.8655 | 0.34 | 3.7651 | 0.17 | |
| 50 | Pagano [49] | 2.9281 | 2.9331 | 2.9281 | |||
| Reddy [11] | 2.8157 | 3.84 | 2.8157 | 4.00 | 2.8157 | 3.84 | |
| Present (NS1) | 2.9149 | 0.45 | 2.9179 | 0.52 | 2.9149 | 0.45 | |
| Present (NS4) | 2.9276 | 0.02 | 2.9350 | 0.06 | 2.9276 | 0.02 | |
| Present (NS6) | 2.9279 | 0.01 | 2.9353 | 0.08 | 2.9279 | 0.01 | |
| z | Sources | ||
|---|---|---|---|
| h/2 | Present (NS2) | 33.5010 | −0.9868 |
| Present (NS4) | 33.9085 | −0.9959 | |
| Present (NS8) | 34.0594 | −0.9988 | |
| FE model | 34.2010 | −1.0152 | |
| 0 a | Present (NS2) | 33.4833 | 0.5994 |
| Present (NS4) | 33.8920 | 0.6149 | |
| Present (NS8) | 34.0404 | 0.6202 | |
| FE model | 34.1334 | 0.6236 | |
| 0 b | Present (NS2) | 22.0173 | 0.0184 |
| Present (NS4) | 21.9642 | 0.0227 | |
| Present (NS8) | 21.9984 | 0.0222 | |
| FE model | 21.9950 | 0.0222 | |
| −h/2 | Present (NS2) | 22.0173 | 0.5998 |
| Present (NS4) | 21.9642 | 0.5970 | |
| Present (NS8) | 21.9984 | 0.5969 | |
| FE model | 21.9950 | 0.5966 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Sheikh, A.H.; Li, G. Analysis of Intact/Delaminated Composite and Sandwich Beams Using a Higher-Order Modeling Technique. J. Compos. Sci. 2024, 8, 175. https://doi.org/10.3390/jcs8050175
Feng Y, Sheikh AH, Li G. Analysis of Intact/Delaminated Composite and Sandwich Beams Using a Higher-Order Modeling Technique. Journal of Composites Science. 2024; 8(5):175. https://doi.org/10.3390/jcs8050175
Chicago/Turabian StyleFeng, Yuan, Abdul Hamid Sheikh, and Guanzhen Li. 2024. "Analysis of Intact/Delaminated Composite and Sandwich Beams Using a Higher-Order Modeling Technique" Journal of Composites Science 8, no. 5: 175. https://doi.org/10.3390/jcs8050175






