Universal Behavior of the Image Resolution for Different Scanning Trajectories
Abstract
:1. Introduction
2. Scanning Methods
2.1. Scanning Trajectory Pattern and Density
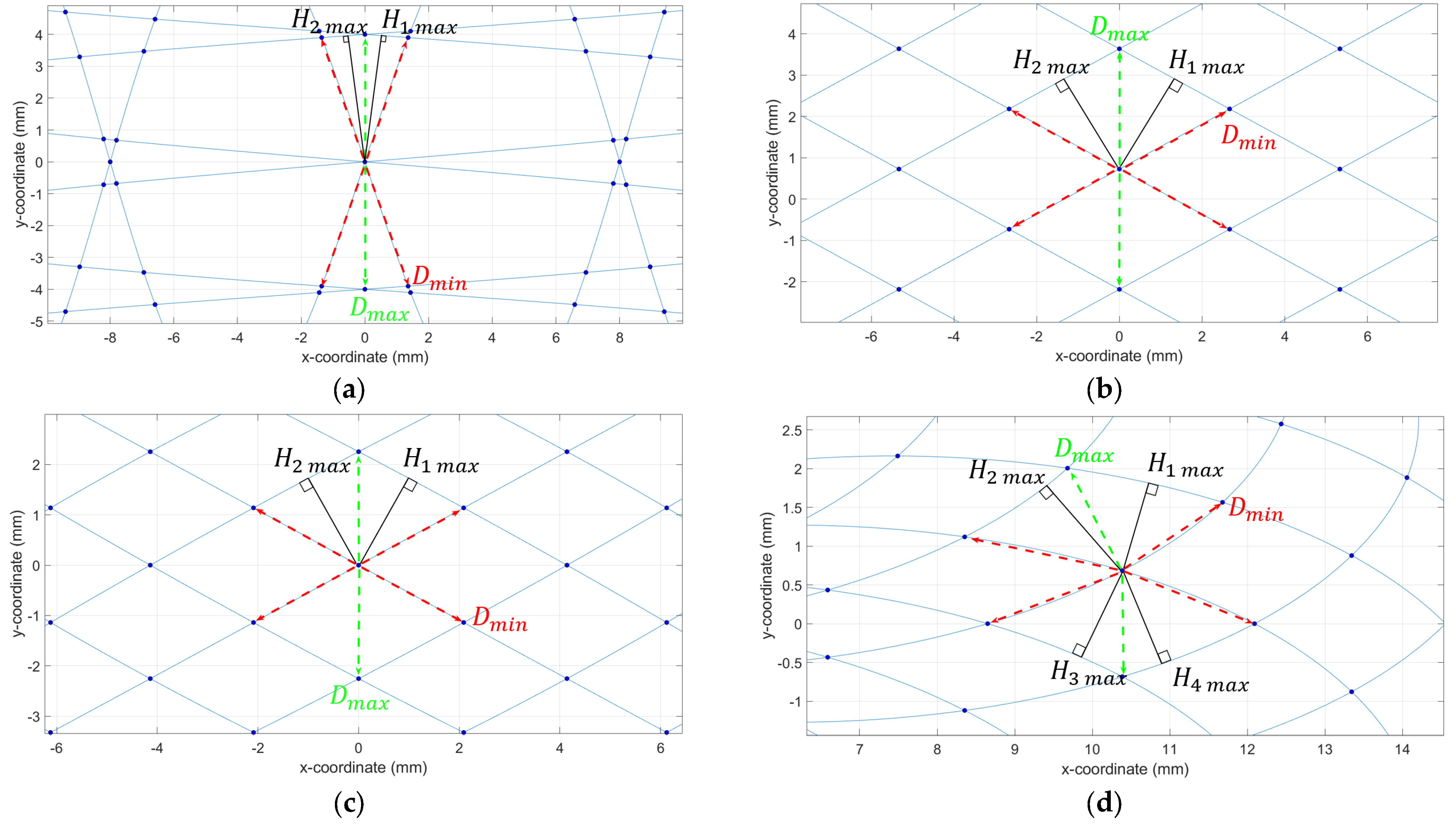
2.2. Scanning Trajectory Characteristics
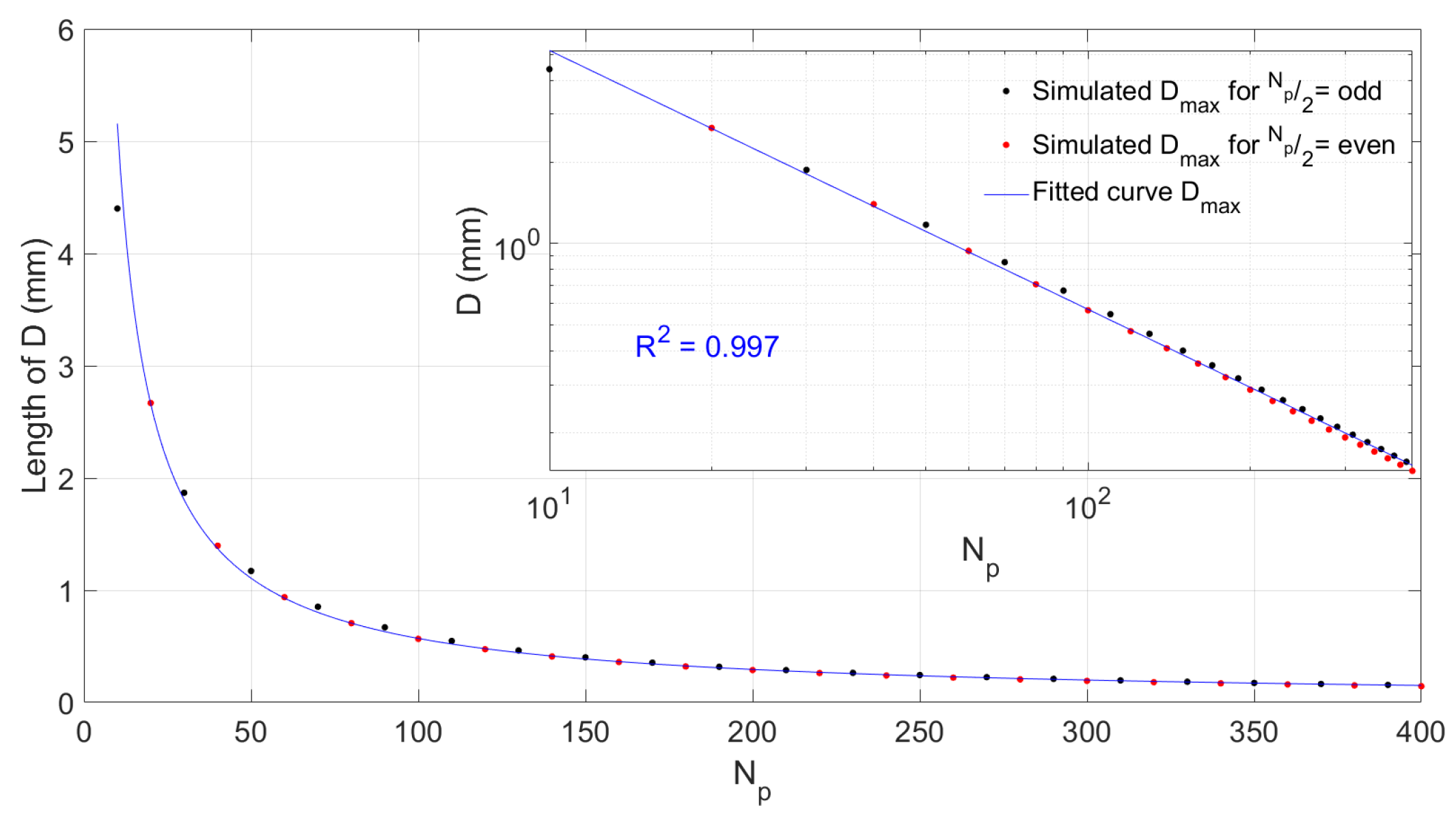
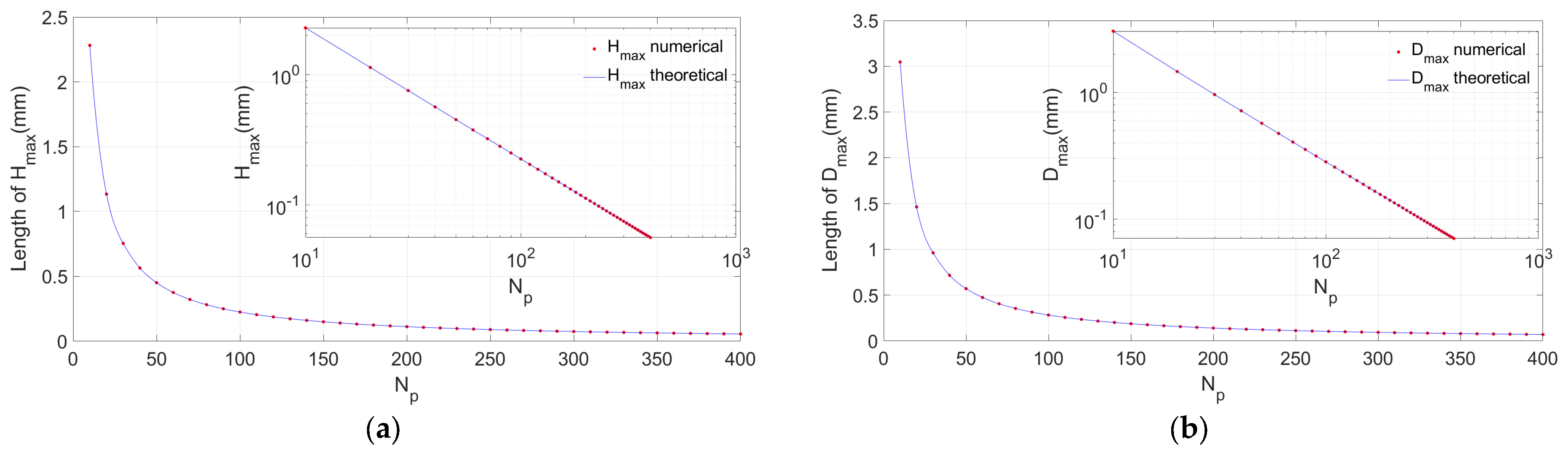
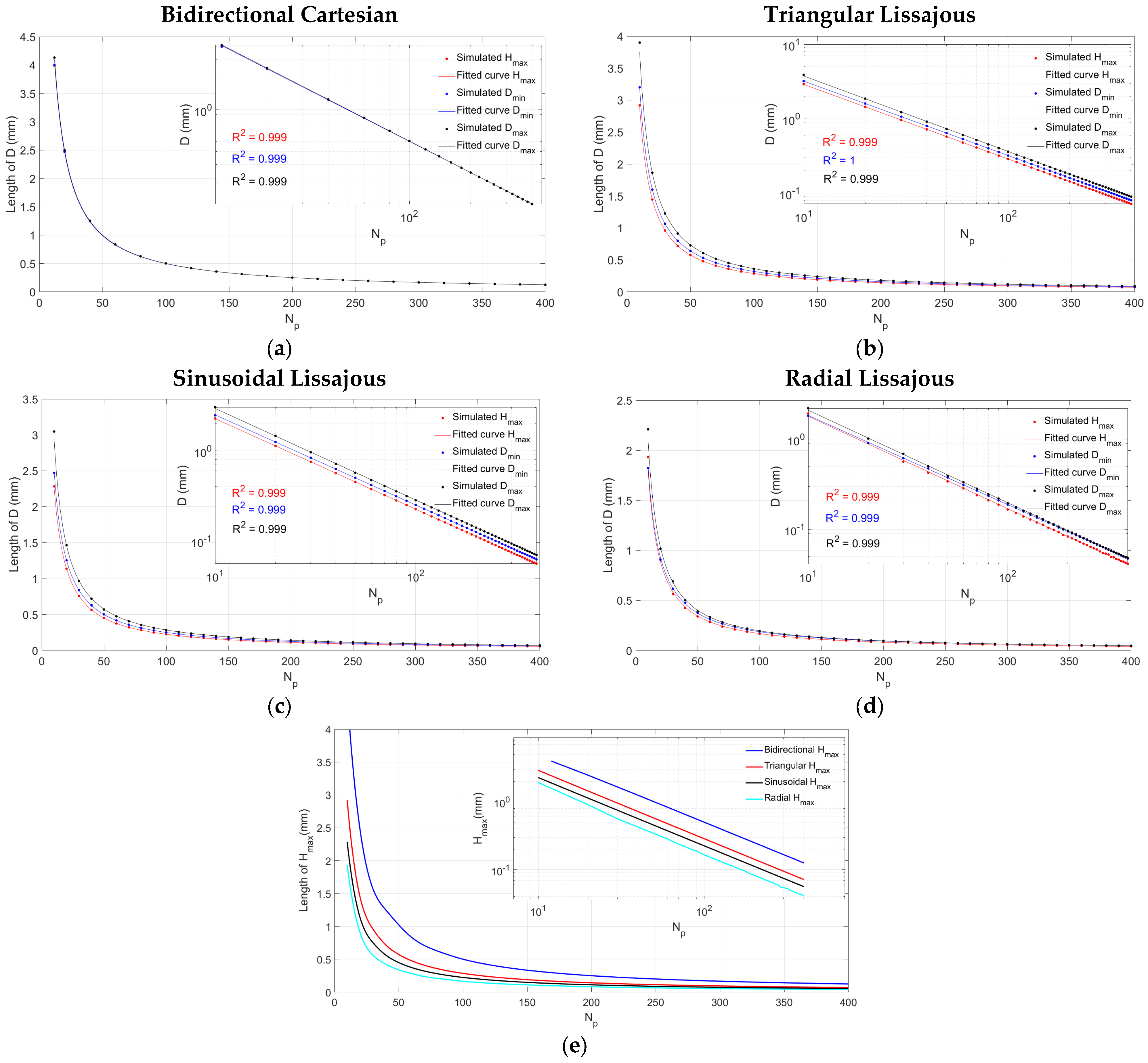
3. Results and Discussion
3.1. Scanning Patterns
3.2. Relationship between Pixel Size and Scanning Parameters
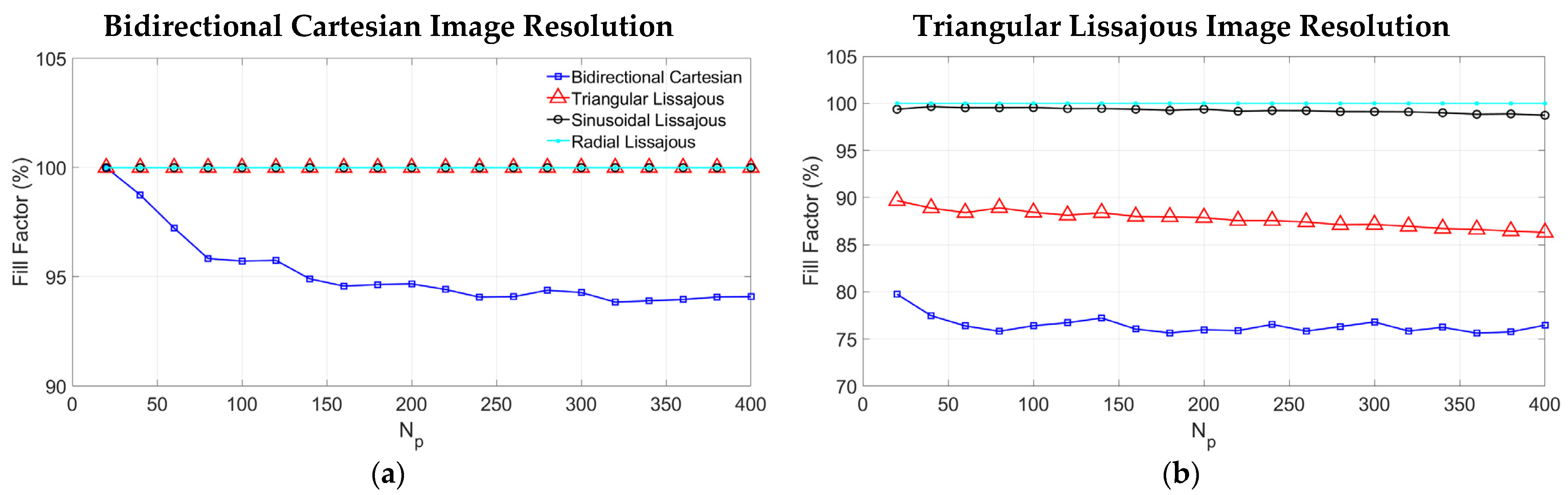
3.3. Scanning Pixel Coverage
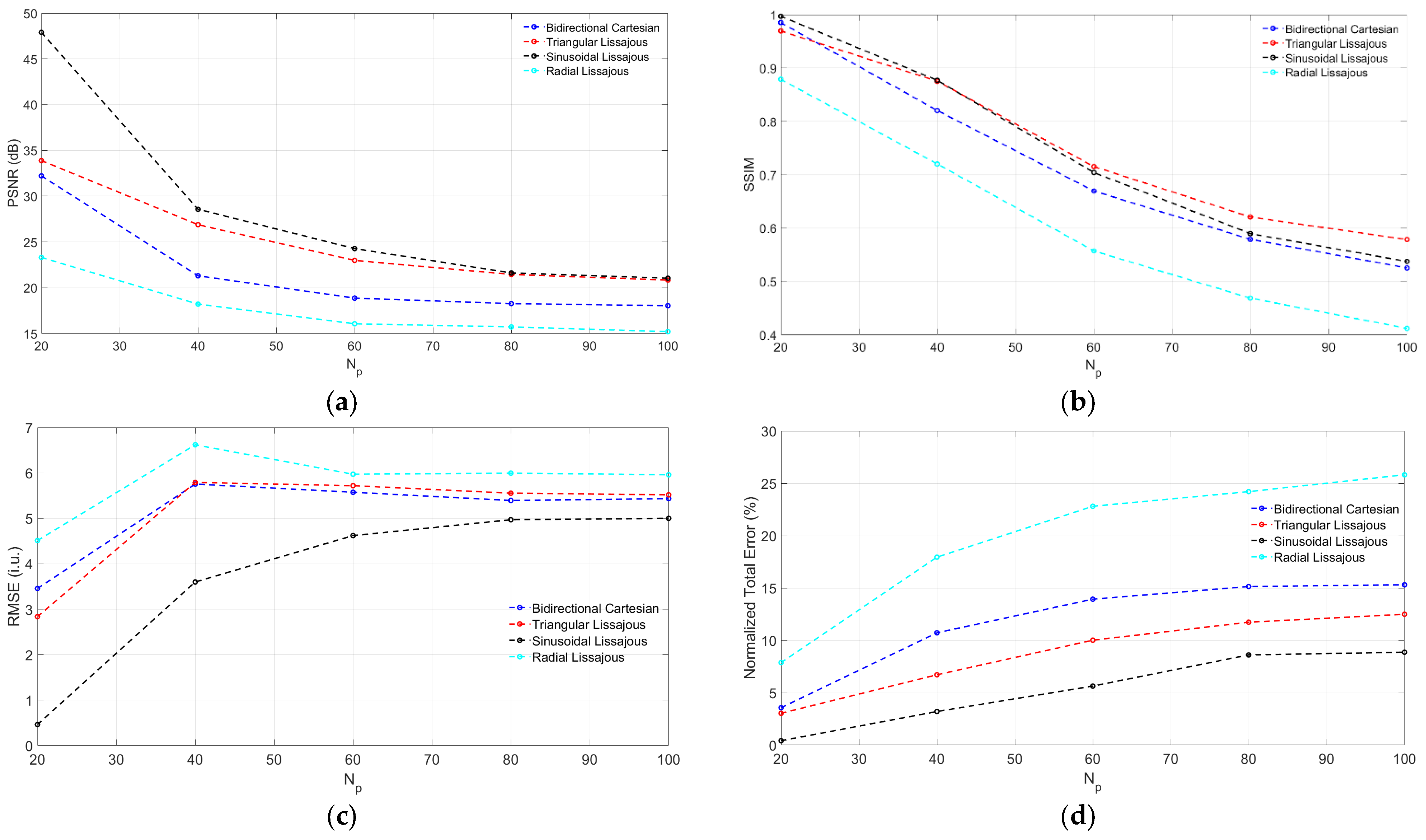
3.4. Image Reconstruction
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A


References
- Bauweraerts, P.; Meyers, J. Reconstruction of turbulent flow fields from lidar measurements using large-eddy simulation. J. Fluid Mech. 2021, 906, A17. [Google Scholar] [CrossRef]
- Wu, J.-W.; Lin, Y.-T.; Lo, Y.-T.; Liu, W.-C.; Fu, L.-C. Lissajous Hierarchical Local Scanning to Increase the Speed of Atomic Force Microscopy. IEEE Trans. Nanotechnol. 2015, 14, 810–819. [Google Scholar] [CrossRef]
- Vinke, E.J.; de Groot, M.; Venkatraghavan, V.; Klein, S.; Niessen, W.J.; Ikram, M.A.; Vernooij, M.W. Trajectories of imaging markers in brain aging: The Rotterdam Study. Neurobiol. Aging 2018, 71, 32–40. [Google Scholar] [CrossRef] [PubMed]
- Kasban, H.; El-Bendary, M.A.M.; Salama, D.H. A Comparative Study of Medical Imaging Techniques. Int. J. Inf. Sci. Intell. Syst. 2015, 4, 37–58. [Google Scholar]
- Weiss, T.; Senouf, O.; Vedula, S.; Michailovich, O.; Zibulevsky, M.; Bronstein, A. PILOT: Physics-Informed Learned Optimized Trajectories for Accelerated MRI. J. Mach. Learn. Biomed. Imaging 2019, 6, 1–23. [Google Scholar] [CrossRef]
- Bogner, W.; Otazo, R.; Henning, A. Accelerated MR spectroscopic imaging—A review of current and emerging techniques. NMR Biomed. 2021, 34, 1–32. [Google Scholar] [CrossRef] [PubMed]
- Werner, F.; Gdaniec, N.; Knopp, T. First experimental comparison between the Cartesian and the Lissajous trajectory for magnetic particle imaging. Phys. Med. Biol. 2017, 62, 3407–3421. [Google Scholar] [CrossRef]
- Knopp, T.; Biederer, S.; Sattel, T.; Weizenecker, J.; Gleich, B.; Borgert, J.; Buzug, T.M. Trajectory analysis for magnetic particle imaging. Phys. Med. Biol. 2009, 54, 385–397. [Google Scholar] [CrossRef]
- Le, T.-A.; Bui, M.P.; Yoon, J. Development of Small-Rabbit-Scale Three-Dimensional Magnetic Particle Imaging System With Amplitude-Modulation-Based Reconstruction. IEEE Trans. Ind. Electron. 2023, 70, 3167–3177. [Google Scholar] [CrossRef]
- Le, T.A.; Bui, M.P.; Yoon, J. Optimal Design and Implementation of a Novel Two-Dimensional Electromagnetic Navigation System That Allows Focused Heating of Magnetic Nanoparticles. IEEE/ASME Trans. Mechatron. 2021, 26, 551–562. [Google Scholar] [CrossRef]
- Mukhatov, A.; Le, T.-A.; Pham, T.T.; Do, T.D. A comprehensive review on magnetic imaging techniques for biomedical applications. Nano Select 2023, 4, 213–230. [Google Scholar] [CrossRef]
- Borcs, A.; Benedek, C. Extraction of Vehicle Groups in Airborne Lidar Point Clouds With Two-Level Point Processes. Geosci. Remote Sens. IEEE Trans. 2015, 53, 1475–1489. [Google Scholar] [CrossRef]
- Leoncini, M.; Bestetti, M.; Bonfanti, A.; Facchinetti, S.; Minotti, P.; Langfelder, G. Fully Integrated, 406 μA, 5/hr, Full Digital Output Lissajous Frequency-Modulated Gyroscope. IEEE Trans. Ind. Electron. 2019, 66, 7386–7396. [Google Scholar] [CrossRef]
- Weiss, U.; Biber, P. Plant detection and mapping for agricultural robots using a 3D LIDAR sensor. Rob. Auton. Syst. 2011, 59, 265–273. [Google Scholar] [CrossRef]
- Fink, M.; Schardt, M.; Baier, V.; Wang, K.; Jakobi, M.; Koch, A.W. Low-cost scanning LIDAR architecture with a scalable frame rate for autonomous vehicles. Appl. Opt. 2023, 62, 675–682. [Google Scholar] [CrossRef]
- Karimi, M.; Oelsch, M.; Stengel, O.; Babaians, E.; Steinbach, E. LoLa-SLAM: Low-Latency LiDAR SLAM Using Continuous Scan Slicing. IEEE Robot. Autom. Lett. 2021, 6, 2248–2255. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, G.; You, Z. Improved sampling scheme for LiDAR in Lissajous scanning mode. Microsyst. Nanoeng. 2022, 8, 64. [Google Scholar] [CrossRef] [PubMed]
- Bazaei, A.; Yong, Y.K.; Moheimani, S.O.R. High-speed Lissajous-scan atomic force microscopy: Scan pattern planning and control design issues. Rev. Sci. Instrum. 2012, 83, 1–10. [Google Scholar] [CrossRef]
- Top, C.B.; Güngör, A. Tomographic Field Free Line Magnetic Particle Imaging with an Open-Sided Scanner Configuration. IEEE Trans. Med. Imaging 2020, 39, 4164–4173. [Google Scholar] [CrossRef]
- von Haxthausen, F.; Böttger, S.; Wulff, D.; Hagenah, J.; García-Vázquez, V.; Ipsen, S. Medical Robotics for Ultrasound Imaging: Current Systems and Future Trends. Curr. Robot. Rep. 2021, 2, 55–71. [Google Scholar] [CrossRef]
- Reinhardt, S.C.M.; Masullo, L.A.; Baudrexel, I.; Steen, P.R.; Kowalewski, R.; Eklund, A.S.; Strauss, S.; Unterauer, E.M.; Schlichthaerle, T.; Strauss, M.T.; et al. Ångström-resolution fluorescence microscopy. Nature 2023, 617, 711–716. [Google Scholar] [CrossRef]
- Vogel, P.; Kampf, T.; Herz, S.; Ruckert, M.A.; Bley, T.A.; Behr, V.C. Adjustable Hardware Lens for Traveling Wave Magnetic Particle Imaging. IEEE Trans. Magn. 2020, 56, 1–6. [Google Scholar] [CrossRef]
- Top, C.B.; Güngör, A.; Ilbey, S.; Güven, H.E. Trajectory analysis for field free line magnetic particle imaging. Med. Phys. 2019, 46, 1592–1607. [Google Scholar] [CrossRef] [PubMed]
- Ozaslan, A.A.; Alacaoglu, A.; Demirel, O.B.; Cukur, T.; Saritas, E.U. Fully automated gridding reconstruction for non-Cartesian x-space magnetic particle imaging. Phys. Med. Biol. 2019, 64, 165018. [Google Scholar] [CrossRef] [PubMed]
- Tanguy, Q.A.A.; Gaiffe, O.; Passilly, N.; Cote, J.-M.; Cabodevila, G.; Bargiel, S.; Lutz, P.; Xie, H.; Gorecki, C. Real-time Lissajous imaging with a low-voltage 2-axis MEMS scanner based on electrothermal actuation. Opt. Express 2020, 28, 8512. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhang, G.; You, Z. Design rules for dense and rapid Lissajous scanning. Microsyst. Nanoeng. 2020, 6, 4–10. [Google Scholar] [CrossRef] [PubMed]
- Bakenecker, A.C.; Ahlborg, M.; Debbeler, C.; Kaethner, C.; Buzug, T.M.; Lüdtke-Buzug, K. Magnetic particle imaging in vascular medicine. Innov. Surg. Sci. 2020, 3, 179–192. [Google Scholar] [CrossRef] [PubMed]
- Boiroux, D.; Oke, Y.; Miwakeichi, F.; Oku, Y. Pixel timing correction in time-lapsed calcium imaging using point scanning microscopy. J. Neurosci. Methods 2014, 237, 60–68. [Google Scholar] [CrossRef] [PubMed]
- Knopp, T.; Buzug, T.M. Magnetic Particle Imaging: An Introduction to Imaging Principles and Scanner Instrumentation; Springer: Berlin/Heidelberg, Germany, 2012; pp. 54–57. ISBN 9783642041990. [Google Scholar]
- Tuma, T.; Lygeros, J.; Kartik, V.; Sebastian, A.; Pantazi, A. High-speed multiresolution scanning probe microscopy based on Lissajous scan trajectories. Nanotechnology 2012, 23, 185501. [Google Scholar] [CrossRef]
- Biederer, S. Magnet-Partikel-Spektrometer: Entwicklung Eines Spektrometers zur Analyse Superparamagnetischer Eisenoxid-Nanopartikel für Magnetic-Particle-Imaging; Springer: Berlin/Heidelberg, Germany, 2012; pp. 14–17. ISBN 3834824070. [Google Scholar]
- Zhang, P.; Liu, J.; Li, Y.; Yin, L.; An, Y.; Zhong, J.; Hui, H.; Tian, J. Dual-Feature Frequency Component Compression Method for Accelerating Reconstruction in Magnetic Particle Imaging. IEEE Trans. Comput. Imaging 2023, 9, 289–297. [Google Scholar] [CrossRef]
- Abdullah-Al-Mamun, M.; Tyagi, V.; Zhao, H. A New Full-Reference Image Quality Metric for Motion Blur Profile Characterization. IEEE Access 2021, 9, 156361–156371. [Google Scholar] [CrossRef]
- Muckley, M.J.; Riemenschneider, B.; Radmanesh, A.; Kim, S.; Jeong, G.; Ko, J.; Jun, Y.; Shin, H.; Hwang, D.; Mostapha, M.; et al. Results of the 2020 fastMRI Challenge for Machine Learning MR Image Reconstruction. IEEE Trans. Med. Imaging 2021, 40, 2306–2317. [Google Scholar] [CrossRef] [PubMed]
- Ahmadian, K.; Reza-Alikhani, H.-R. Self-Organized Maps and High-Frequency Image Detail for MRI Image Enhancement. IEEE Access 2021, 9, 145662–145682. [Google Scholar] [CrossRef]
- Duan, J.; Liu, C.; Liu, Y.; Shang, Z. Adaptive Transform Learning and Joint Sparsity Based PLORAKS Parallel Magnetic Resonance Image Reconstruction. IEEE Access 2020, 8, 212315–212326. [Google Scholar] [CrossRef]
- Wang, J.; Qiao, L.; Lv, H.; Lv, Z. Deep Transfer Learning-Based Multi-Modal Digital Twins for Enhancement and Diagnostic Analysis of Brain MRI Image. IEEE/ACM Trans. Comput. Biol. Bioinform. 2023, 20, 2407–2419. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Preuhs, A.; Manhart, M.; Lauritsch, G.; Maier, A. Data Extrapolation From Learned Prior Images for Truncation Correction in Computed Tomography. IEEE Trans. Med. Imaging 2021, 40, 3042–3053. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Sun, Y.; Liao, J.; Cao, R.; Wang, C.; Jin, L.; Feng, J.; Cao, C. Image Reconstruction of Targets Undergoing Complex Motion Based on Optical Phased Array Compressed-Sensing Ghost Imaging Technology. J. Light. Technol. 2022, 40, 7746–7756. [Google Scholar] [CrossRef]
- Mukaddim, R.A.; Meshram, N.H.; Weichmann, A.M.; Mitchell, C.C.; Varghese, T. Spatiotemporal Bayesian Regularization for Cardiac Strain Imaging: Simulation and In Vivo Results. IEEE Open J. Ultrason. Ferroelectr. Freq. Control 2021, 1, 21–36. [Google Scholar] [CrossRef]



| Trajectories | Mathematical Expression | Frequency Ratio and Repetition Time | Advantages | Disadvantages | |
|---|---|---|---|---|---|
| Bidirectional Cartesian [24] | (3) |
|
| ||
| (4) | |||||
| Triangular Lissajous [8] | (5) |
|
| ||
| (6) | |||||
| Sinusoidal Lissajous [8] | (7) |
|
| ||
| (8) | |||||
| Radial Lissajous [24] | (9) |
|
| ||
| (10) | |||||
| B.C. | 0.502 | 0.502 | 0.503 |
| T.L. | 0.287 | 0.320 | 0.361 |
| S.L. | 0.225 | 0.251 | 0.283 |
| R.L. | 0.166 | 0.188 | 0.195 |
| B.C. | T.L. | S.L. | R.L. | ||
|---|---|---|---|---|---|
| Max | 0.991 | 1.003 | 1.003 | 1.026 | |
| 0.021 | 0.034 | 0.044 | 0.052 | ||
| Max | 0.992 | 1.000 | 0.998 | 0.991 | |
| 0.021 | 0.031 | 0.040 | 0.056 | ||
| Max | 0.997 | 1.014 | 1.014 | 1.028 | |
| 0.020 | 0.026 | 0.033 | 0.045 |
| B.C. | T.L. | S.L. | R.L. | ||
|---|---|---|---|---|---|
| Max | 0.022 | 0.034 | 0.043 | 0.046 | |
| 0.999 | 0.999 | 0.999 | 0.999 | ||
| Max | 0.022 | 0.031 | 0.040 | 0.058 | |
| 0.999 | 1.000 | 0.999 | 0.999 | ||
| Max | 0.020 | 0.024 | 0.031 | 0.040 | |
| 0.999 | 0.999 | 0.999 | 0.998 |
| Pixel Size | 0.5 of BC mesh |
| Values | 20, 40, 60, 80, 100 |
| Particle Diameter | 30 × 10−9 m |
| Temperature | 310 K |
| Permeability of Air | 4π × 10−7 N/A2 |
| Concentration of Particles | 1.5 mol/m3 |
| Molar Mass of SPION | 0.231 kg/mol |
| Density of SPION | 5170 kg/m3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mukhatov, A.; Le, T.-A.; Do, T.D.; Pham, T.T. Universal Behavior of the Image Resolution for Different Scanning Trajectories. Appl. Syst. Innov. 2023, 6, 103. https://doi.org/10.3390/asi6060103
Mukhatov A, Le T-A, Do TD, Pham TT. Universal Behavior of the Image Resolution for Different Scanning Trajectories. Applied System Innovation. 2023; 6(6):103. https://doi.org/10.3390/asi6060103
Chicago/Turabian StyleMukhatov, Azamat, Tuan-Anh Le, Ton Duc Do, and Tri T. Pham. 2023. "Universal Behavior of the Image Resolution for Different Scanning Trajectories" Applied System Innovation 6, no. 6: 103. https://doi.org/10.3390/asi6060103





