Simulating Binary Neutron Stars with Hybrid Equation of States: Gravitational Waves, Electromagnetic Signatures and Challenges for Numerical Relativity
Abstract
1. Introduction
2. A New Hybrid Star Equation of State
2.1. tdBag Model for Strange Quark Matter
- The quartic coefficient can be interpreted as a correction to the pressure of the free Fermi sea arising from quantum chromodynamics (QCD). Fraga et al. [41] show that, to second order in the strong coupling constant, a reasonable value for this parameter is . The values of and correspond to maximum or none QCD interaction, respectively.
- The bag constant B, introduced phenomenologically into the theory to describe the deconfinement, is the energy density required to produce a “vacuumless” volume in which quarks exist.
- The contribution of the electron potential () for our purposes is negligible; cf. Reference [43] and references therein. Nevertheless, if the SQM is not in the CFL phase [40] there must be electrons within the quark phase to ensure (i) local charge neutrality and (ii) chemical equilibrium. These two conditions may be expressed respectively aswhere denotes the number density. For SQM in the CFL phase, the quark matter is symmetric, thus, local charge neutrality is satisfied without the presence of electrons. In both cases, CFL () or non-CFL phase (neglecting ), Equation (1) leads to an analytical EoS for SQM.
2.2. Thermodynamics and Parameter Analysis
- (i)
- : not allowed region due to the fact that hadronic matter is more stable than quark matter, then we cannot use a SQM EoS.
- (ii)
- : absolutely stable strange stars (SS). There is no phase transition HM → SQM and the star is entirely made of 3-flavor quarks.
- (iii)
- : HyS. There exists a phase transition between HM and SQM for some energy density .
- (i)
- : HM EoS,
- (ii)
- : ,
- (iii)
- : SQM EoS.
2.3. Building Hybrid Star EoS
2.4. HyS EoS as Piecewise Polytropes
3. Configurations Details and Numerical Methods
3.1. Hybrid Star Configuration
3.2. Numerical Methods
4. Quantitative Merger Dynamics
5. Gravitational Wave Signal
5.1. The Inspiral
5.2. The Postmerger
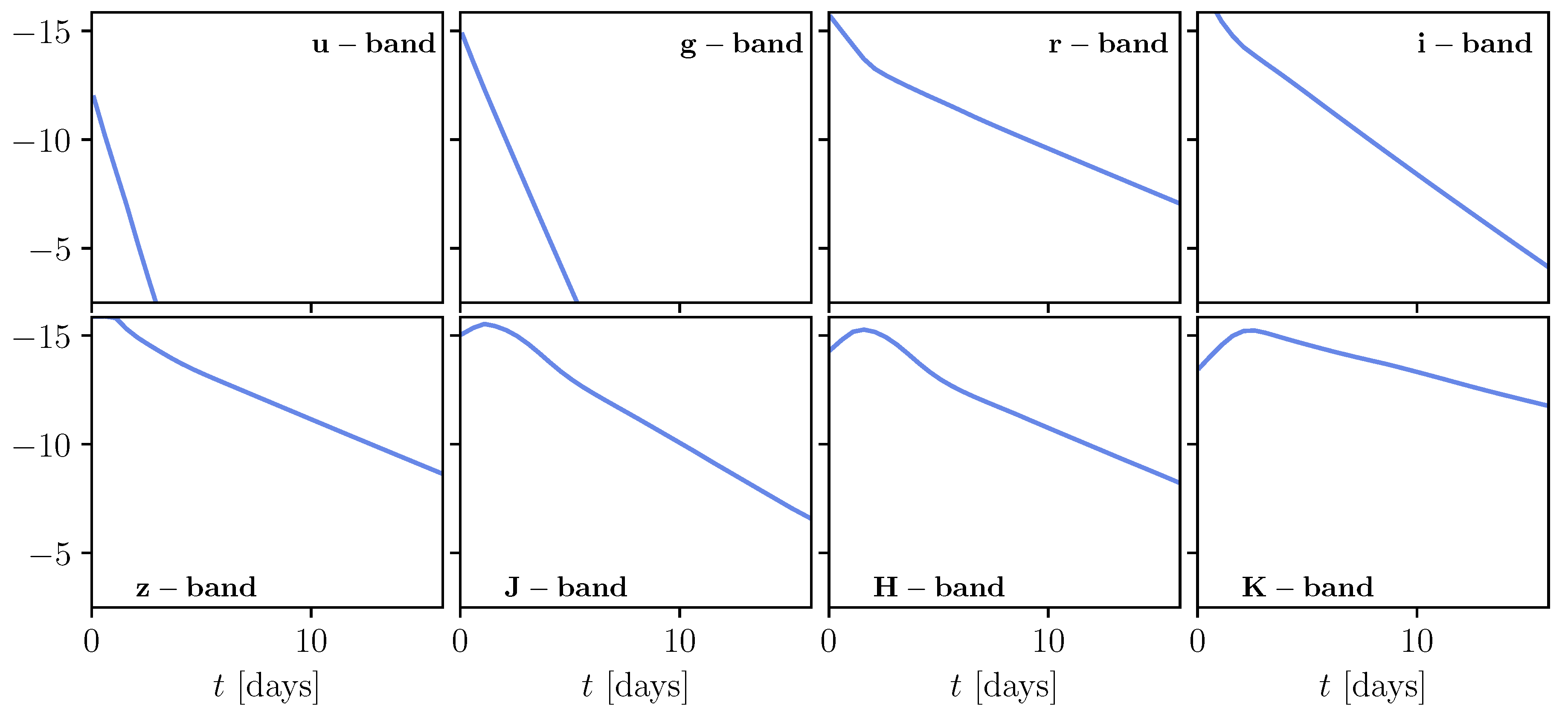
6. Ejecta and Electromagnetic Counterparts
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BH | Black Hole |
| BNS | Binary Neutron Star |
| CFL | Color-flavor-locked |
| EM | Electromagnetic |
| EoS | Equation of State |
| GRB | Gamma Ray Burst |
| GRHD | General Relativistic Hydrodynamics |
| GW | Gravitational Wave |
| HM | Hadronic Matter |
| HRSC | High-resolution Shock-capturing |
| HyS | Hybrid Star |
| LLF | Local Lax-Friedrich |
| MIT | Massachusetts Institute of Technology |
| NR | Numerical Relativity |
| NS | Neutron Star |
| QCD | Quantum Chromodynamics |
| SQM | Strange Quark Matter |
| WENOZ | Weighted Essentially Non-oscillatory |
Appendix A. HyS Piecewise Polytrope
| K | ||
|---|---|---|
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. 2017, 848, L12. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. 2017, 848, L13. [Google Scholar] [CrossRef]
- Dai, L.; Venumadhav, T.; Zackay, B. Parameter Estimation for GW170817 using Relative Binning. arXiv 2018, arXiv:1806.08793. [Google Scholar]
- De, S.; Finstad, D.; Lattimer, J.M.; Brown, D.A.; Berger, E.; Biwer, C.M. Tidal Deformabilities and Radii of Neutron Stars from the Observation of GW170817. Phys. Rev. Lett. 2018, 121, 091102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Properties of the binary neutron star merger GW170817. Phys. Rev. 2019, X9, 011001. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Measurements of neutron star radii and equation of state. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo during the First and Second Observing Runs. arXiv 2018, arXiv:1811.12907. [Google Scholar]
- Radice, D.; Perego, A.; Zappa, F.; Bernuzzi, S. GW170817: Joint Constraint on the Neutron Star Equation of State from Multimessenger Observations. Astrophys. J. 2018, 852, L29. [Google Scholar] [CrossRef]
- Bauswein, A.; Just, O.; Janka, H.T.; Stergioulas, N. Neutron-star radius constraints from GW170817 and future detections. Astrophys. J. 2017, 850, L34. [Google Scholar] [CrossRef]
- Coughlin, M.W.; Dietrich, T.; Doctor, Z.; Kasen, D.; Coughlin, S.; Jerkstrand, A.; Leloudas, G.; McBrien, O.; Metzger, B.D.; O’Shaughnessy, R.; et al. Constraints on the neutron star equation of state from AT2017gfo using radiative transfer simulations. Mon. Not. R. Astron. Soc. 2018, 480. [Google Scholar] [CrossRef]
- Radice, D.; Dai, L. Multimessenger Parameter Estimation of GW170817. arXiv 2018, arXiv:1810.12917. [Google Scholar] [CrossRef]
- Coughlin, M.W.; Dietrich, T.; Margalit, B.; Metzger, B.D. Multi-messenger Bayesian parameter inference of a binary neutron-star merger. arXiv 2018, arXiv:1812.04803. [Google Scholar]
- Annala, E.; Gorda, T.; Kurkela, A.; Vuorinen, A. Gravitational-wave constraints on the neutron-star-matter Equation of State. Phys. Rev. Lett. 2018, 120, 172703. [Google Scholar] [CrossRef] [PubMed]
- Most, E.R.; Weih, L.R.; Rezzolla, L.; Schaffner-Bielich, J. New constraints on radii and tidal deformabilities of neutron stars from GW170817. Phys. Rev. Lett. 2018, 120, 261103. [Google Scholar] [CrossRef] [PubMed]
- Annala, E.; Gorda, T.; Kurkela, A.; Nättilä, J.; Vuorinen, A. Quark-matter cores in neutron stars. arXiv 2019, arXiv:1903.09121. [Google Scholar]
- Most, E.R.; Papenfort, L.J.; Dexheimer, V.; Hanauske, M.; Schramm, S.; Stöcker, H.; Rezzolla, L. Signatures of quark-hadron phase transitions in general-relativistic neutron-star mergers. Phys. Rev. Lett. 2019, 122, 061101. [Google Scholar] [CrossRef] [PubMed]
- Bauswein, A.; Bastian, N.U.F.; Blaschke, D.B.; Chatziioannou, K.; Clark, J.A.; Fischer, T.; Oertel, M. Identifying a first-order phase transition in neutron star mergers through gravitational waves. Phys. Rev. Lett. 2019, 122, 061102. [Google Scholar] [CrossRef]
- Radice, D.; Rezzolla, L.; Galeazzi, F. Beyond second-order convergence in simulations of binary neutron stars in full general-relativity. Mon. Not. R. Astron. Soc. 2014, 437, L46–L50. [Google Scholar] [CrossRef]
- Hotokezaka, K.; Kyutoku, K.; Okawa, H.; Shibata, M. Exploring tidal effects of coalescing binary neutron stars in numerical relativity. II. Long-term simulations. Phys. Rev. 2015, D91, 064060. [Google Scholar] [CrossRef]
- Dietrich, T.; Bernuzzi, S.; Tichy, W. Closed-form tidal approximants for binary neutron star gravitational waveforms constructed from high-resolution numerical relativity simulations. Phys. Rev. 2017, D96, 121501. [Google Scholar] [CrossRef]
- Kiuchi, K.; Kawaguchi, K.; Kyutoku, K.; Sekiguchi, Y.; Shibata, M.; Taniguchi, K. Sub-radian-accuracy gravitational waveforms of coalescing binary neutron stars in numerical relativity. Phys. Rev. 2017, D96, 084060. [Google Scholar] [CrossRef]
- Dietrich, T.; Radice, D.; Bernuzzi, S.; Zappa, F.; Perego, A.; Brügmann, B.; Chaurasia, S.V.; Dudi, R.; Tichy, W.; Ujevic, M. CoRe database of binary neutron star merger waveforms. Class. Quant. Grav. 2018, 35, 24LT01. [Google Scholar] [CrossRef]
- Rezzolla, L.; Giacomazzo, B.; Baiotti, L.; Granot, J.; Kouveliotou, C.; Aloy, M.A. The missing link: Merging neutron stars naturally produce jet-like structures and can power short Gamma-Ray Bursts. Astrophys. J. 2011, 732, L6. [Google Scholar] [CrossRef]
- Neilsen, D.; Liebling, S.L.; Anderson, M.; Lehner, L.; O’Connor, E.; Palenzuela, C. Magnetized Neutron Stars With Realistic Equations of State and Neutrino Cooling. Phys. Rev. 2014, D89, 104029. [Google Scholar] [CrossRef]
- Sekiguchi, Y.; Kiuchi, K.; Kyutoku, K.; Shibata, M. Dynamical mass ejection from binary neutron star mergers: Radiation-hydrodynamics study in general relativity. Phys. Rev. 2015, D91, 064059. [Google Scholar] [CrossRef]
- Palenzuela, C.; Liebling, S.L.; Neilsen, D.; Lehner, L.; Caballero, O.L.; O’Connor, E.; Anderson, M. Effects of the microphysical Equation of State in the mergers of magnetized Neutron Stars With Neutrino Cooling. Phys. Rev. 2015, D92, 044045. [Google Scholar] [CrossRef]
- Foucart, F. Monte Carlo closure for moment-based transport schemes in general relativistic radiation hydrodynamic simulations. Mon. Not. R. Astron. Soc. 2018, 475, 4186–4207. [Google Scholar] [CrossRef]
- Ruiz, M.; Shapiro, S.L.; Tsokaros, A. GW170817, General Relativistic Magnetohydrodynamic Simulations, and the Neutron Star Maximum Mass. Phys. Rev. 2018, D97, 021501. [Google Scholar] [CrossRef]
- Ciolfi, R.; Kastaun, W.; Giacomazzo, B.; Endrizzi, A.; Siegel, D.M.; Perna, R. General relativistic magnetohydrodynamic simulations of binary neutron star mergers forming a long-lived neutron star. Phys. Rev. 2017, D95, 063016. [Google Scholar] [CrossRef]
- Kiuchi, K.; Kyutoku, K.; Sekiguchi, Y.; Shibata, M. Global simulations of strongly magnetized remnant massive neutron stars formed in binary neutron star mergers. Phys. Rev. 2018, D97, 124039. [Google Scholar] [CrossRef]
- Radice, D. General-Relativistic Large-Eddy Simulations of Binary Neutron Star Mergers. Astrophys. J. 2017, 838, L2. [Google Scholar] [CrossRef]
- Shibata, M.; Kiuchi, K.; Sekiguchi, Y.i. General relativistic viscous hydrodynamics of differentially rotating neutron stars. Phys. Rev. 2017, D95, 083005. [Google Scholar] [CrossRef]
- Pietri, R.d.; Drago, A.; Feo, A.; Pagliara, G.; Pasquali, M.; Traversi, S.; Wiktorowicz, G. Merger of Compact Stars in the Two-Families Scenario. arXiv 2019, arXiv:1904.01545. [Google Scholar]
- Farhi, E.; Jaffe, R.L. Strange Matter. Phys. Rev. 1984, D30, 2379. [Google Scholar] [CrossRef]
- Chodos, A.; Jaffe, R.L.; Johnson, K.; Thorn, C.B.; Weisskopf, V.F. A New Extended Model of Hadrons. Phys. Rev. 1974, D9, 3471–3495. [Google Scholar] [CrossRef]
- Detar, C.E. The MIT bag model. In Quantum Flavordynamics, Quantum Chromodynamics and Unified Theories; Plenum Press: New York, NY, USA, 1979; p. 393. [Google Scholar]
- Alford, M.; Braby, M.; Paris, M.W.; Reddy, S. Hybrid stars that masquerade as neutron stars. Astrophys. J. 2005, 629, 969–978. [Google Scholar] [CrossRef]
- Alford, M.G.; Schmitt, A.; Rajagopal, K.; Schäfer, T. Color superconductivity in dense quark matter. Rev. Mod. Phys. 2008, 80, 1455–1515. [Google Scholar] [CrossRef]
- Lugones, G.; Horvath, J.E. Color flavor locked strange matter. Phys. Rev. 2002, D66, 074017. [Google Scholar] [CrossRef]
- Fraga, E.S.; Pisarski, R.D.; Schaffner-Bielich, J. Small, dense quark stars from perturbative QCD. Phys. Rev. 2001, D63, 121702. [Google Scholar] [CrossRef]
- Klahn, T.; Fischer, T. Vector interaction enhanced bag model for astrophysical applications. Astrophys. J. 2015, 810, 134. [Google Scholar] [CrossRef]
- Pereira, J.P.; Flores, C.V.; Lugones, G. Phase transition effects on the dynamical stability of hybrid neutron stars. Astrophys. J. 2018, 860, 12. [Google Scholar] [CrossRef]
- Bodmer, A.R. Collapsed nuclei. Phys. Rev. 1971, D4, 1601–1606. [Google Scholar] [CrossRef]
- Witten, E. Cosmic Separation of Phases. Phys. Rev. 1984, D30, 272–285. [Google Scholar] [CrossRef]
- Glendenning, N.K. Compact Stars: Nuclear Physics, Particle Physics, and General Relativity, 2nd ed.; Springer: New York, NY, USA, 2000. [Google Scholar]
- Lugones, G.; Grunfeld, A.G.; Al Ajmi, M. Surface tension and curvature energy of quark matter in the Nambu-Jona-Lasinio model. Phys. Rev. 2013, C88, 045803. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. 1. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef]
- Douchin, F.; Haensel, P. A unified equation of state of dense matter and neutron star structure. Astron. Astrophys. 2001, 380, 151. [Google Scholar] [CrossRef]
- Bruegmann, B.; Gonzalez, J.A.; Hannam, M.; Husa, S.; Sperhake, U.; Tichy, W. Calibration of Moving Puncture Simulations. Phys. Rev. 2008, D77, 024027. [Google Scholar] [CrossRef]
- Thierfelder, M.; Bernuzzi, S.; Bruegmann, B. Numerical relativity simulations of binary neutron stars. Phys. Rev. 2011, D84, 044012. [Google Scholar] [CrossRef]
- Dietrich, T.; Bernuzzi, S.; Ujevic, M.; Brügmann, B. Numerical relativity simulations of neutron star merger remnants using conservative mesh refinement. Phys. Rev. 2015, D91, 124041. [Google Scholar] [CrossRef]
- Bernuzzi, S.; Dietrich, T. Gravitational waveforms from binary neutron star mergers with high-order weighted-essentially-nonoscillatory schemes in numerical relativity. Phys. Rev. 2016, D94, 064062. [Google Scholar] [CrossRef]
- Tichy, W. A New numerical method to construct binary neutron star initial data. Class. Quant. Grav. 2009, 26, 175018. [Google Scholar] [CrossRef]
- Read, J.S.; Lackey, B.D.; Owen, B.J.; Friedman, J.L. Constraints on a phenomenologically parameterized neutron-star equation of state. Phys. Rev. 2009, D79, 124032. [Google Scholar] [CrossRef]
- Wilson, J.R.; Mathews, G.J. Instabilities in Close Neutron Star Binaries. Phys. Rev. Lett. 1995, 75, 4161–4164. [Google Scholar] [CrossRef] [PubMed]
- Wilson, J.R.; Mathews, G.J.; Marronetti, P. Relativistic numerical model for close neutron star binaries. Phys. Rev. 1996, D54, 1317–1331. [Google Scholar] [CrossRef]
- York, J.W., Jr. Conformal ’thin sandwich’ data for the initial-value problem. Phys. Rev. Lett. 1999, 82, 1350–1353. [Google Scholar] [CrossRef]
- Tichy, W. Constructing quasi-equilibrium initial data for binary neutron stars with arbitrary spins. Phys. Rev. D 2012, 86, 064024. [Google Scholar] [CrossRef]
- Dietrich, T.; Moldenhauer, N.; Johnson-McDaniel, N.K.; Bernuzzi, S.; Markakis, C.M.; Brügmann, B.; Tichy, W. Binary Neutron Stars with Generic Spin, Eccentricity, Mass ratio, and Compactness–Quasi-equilibrium Sequences and First Evolutions. Phys. Rev. 2015, D92, 124007. [Google Scholar] [CrossRef]
- Moldenhauer, N.; Markakis, C.M.; Johnson-McDaniel, N.K.; Tichy, W.; Brügmann, B. Initial data for binary neutron stars with adjustable eccentricity. Phys. Rev. 2014, D90, 084043. [Google Scholar] [CrossRef]
- Kyutoku, K.; Shibata, M.; Taniguchi, K. Reducing orbital eccentricity in initial data of binary neutron stars. Phys. Rev. 2014, D90, 064006. [Google Scholar] [CrossRef]
- Bernuzzi, S.; Hilditch, D. Constraint violation in free evolution schemes: Comparing BSSNOK with a conformal decomposition of Z4. Phys. Rev. 2010, D81, 084003. [Google Scholar] [CrossRef]
- Weyhausen, A.; Bernuzzi, S.; Hilditch, D. Constraint damping for the Z4c formulation of general relativity. Phys. Rev. 2012, D85, 024038. [Google Scholar] [CrossRef]
- Hilditch, D.; Bernuzzi, S.; Thierfelder, M.; Cao, Z.; Tichy, W.; Bruegmann, B. Compact binary evolutions with the Z4c formulation. Phys. Rev. 2013, D88, 084057. [Google Scholar] [CrossRef]
- Borges, R.; Carmona, M.; Costa, B.; Don, W.S. An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws. J. Comput. Phys. 2008, 227, 3191–3211. [Google Scholar] [CrossRef]
- Dietrich, T.; Bernuzzi, S.; Bruegmann, B.; Tichy, W. High-resolution numerical relativity simulations of spinning binary neutron star mergers. In Proceedings of the 26th Euromicro International Conference on Parallel, Distributed and Network-based Processing (PDP 2018), Cambridge, UK, 21–23 March 2018; pp. 682–689. [Google Scholar] [CrossRef]
- Faber, J.A.; Rasio, F.A. Binary Neutron Star Mergers. Living Rev. Rel. 2012, arXiv:1204.385815, 8. [Google Scholar] [CrossRef] [PubMed]
- Dietrich, T.; Ujevic, M.; Tichy, W.; Bernuzzi, S.; Bruegmann, B. Gravitational waves and mass ejecta from binary neutron star mergers: Effect of the mass-ratio. Phys. Rev. 2017, D95, 024029. [Google Scholar] [CrossRef]
- Dietrich, T.; Bernuzzi, S.; Ujevic, M.; Tichy, W. Gravitational waves and mass ejecta from binary neutron star mergers: Effect of the stars’ rotation. Phys. Rev. 2017, D95, 044045. [Google Scholar] [CrossRef]
- Dietrich, T.; Khan, S.; Dudi, R.; Kapadia, S.J.; Kumar, P.; Nagar, A.; Ohme, F.; Pannarale, F.; Samajdar, A.; Bernuzzi, S.; et al. Matter imprints in waveform models for neutron star binaries: Tidal and self-spin effects. Phys. Rev. 2019, D99, 024029. [Google Scholar] [CrossRef]
- Hannam, M.; Schmidt, P.; Bohé, A.; Haegel, L.; Husa, S.; Ohme, F.; Pratten, G.; Pürrer, M. Simple Model of Complete Precessing Black-Hole-Binary Gravitational Waveforms. Phys. Rev. Lett. 2014, 113, 151101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Tests of General Relativity with GW170817. Phys. Rev. Lett. 2018, 123, 011102. [Google Scholar] [CrossRef]
- Takami, K.; Rezzolla, L.; Baiotti, L. Constraining the Equation of State of Neutron Stars from Binary Mergers. Phys. Rev. Lett. 2014, 113, 091104. [Google Scholar] [CrossRef] [PubMed]
- Takami, K.; Rezzolla, L.; Baiotti, L. Spectral properties of the post-merger gravitational-wave signal from binary neutron stars. Phys. Rev. 2015, D91, 064001. [Google Scholar] [CrossRef]
- Rezzolla, L.; Takami, K. Gravitational-wave signal from binary neutron stars: a systematic analysis of the spectral properties. Phys. Rev. 2016, D93, 124051. [Google Scholar] [CrossRef]
- Bauswein, A.; Janka, H.T. Measuring neutron-star properties via gravitational waves from binary mergers. Phys. Rev. Lett. 2012, 108, 011101. [Google Scholar] [CrossRef]
- Stergioulas, N.; Bauswein, A.; Zagkouris, K.; Janka, H.T. Gravitational waves and nonaxisymmetric oscillation modes in mergers of compact object binaries. Mon. Not. R. Astron. Soc. 2011, 418, 427. [Google Scholar] [CrossRef]
- Bauswein, A.; Janka, H.T.; Hebeler, K.; Schwenk, A. Equation-of-state dependence of the gravitational-wave signal from the ring-down phase of neutron-star mergers. Phys. Rev. 2012, D86, 063001. [Google Scholar] [CrossRef]
- Bauswein, A.; Stergioulas, N.; Janka, H.T. Revealing the high-density equation of state through binary neutron star mergers. Phys. Rev. 2014, D90, 023002. [Google Scholar] [CrossRef]
- Clark, J.A.; Bauswein, A.; Stergioulas, N.; Shoemaker, D. Observing Gravitational Waves From The Post-Merger Phase Of Binary Neutron Star Coalescence. Class. Quant. Grav. 2016, 33, 085003. [Google Scholar] [CrossRef]
- Bauswein, A.; Stergioulas, N. Unified picture of the post-merger dynamics and gravitational wave emission in neutron star mergers. Phys. Rev. 2015, D91, 124056. [Google Scholar] [CrossRef]
- Bernuzzi, S.; Dietrich, T.; Nagar, A. Modeling the complete gravitational wave spectrum of neutron star mergers. Phys. Rev. Lett. 2015, 115, 091101. [Google Scholar] [CrossRef]
- Chaurasia, S.V.; Dietrich, T.; Johnson-McDaniel, N.K.; Ujevic, M.; Tichy, W.; Brügmann, B. Gravitational waves and mass ejecta from binary neutron star mergers: Effect of large eccentricities. Phys. Rev. 2018, D98, 104005. [Google Scholar] [CrossRef]
- Metzger, B.D. Kilonovae. Living Rev. Rel. 2017, 20, 3. [Google Scholar] [CrossRef] [PubMed]
- Dietrich, T.; Ujevic, M. Modeling dynamical ejecta from binary neutron star mergers and implications for electromagnetic counterparts. Class. Quant. Grav. 2017, 34, 105014. [Google Scholar] [CrossRef]
- Kohri, K.; Narayan, R.; Piran, T. Neutrino-dominated accretion and supernovae. Astrophys. J. 2005, 629, 341–361. [Google Scholar] [CrossRef]
- Surman, R.; McLaughlin, G.C.; Hix, W.R. Nucleosynthesis in the outflow from gamma-ray burst accretion disks. Astrophys. J. 2006, 643, 1057–1064. [Google Scholar] [CrossRef]
- Metzger, B.D.; Piro, A.L.; Quataert, E. Time-Dependent Models of Accretion Disks Formed from Compact Object Mergers. Mon. Not. R. Astron. Soc. 2008, 390, 781. [Google Scholar] [CrossRef]
- Dessart, L.; Ott, C.D.; Burrows, A.; Rosswog, S.; Livne, E. Neutrino signatures and the neutrino-driven wind in Binary Neutron Star Mergers. Astrophys. J. 2009, 690, 1681. [Google Scholar] [CrossRef]
- Fernández, R.; Metzger, B.D. Delayed outflows from black hole accretion tori following neutron star binary coalescence. Mon. Not. R. Astron. Soc. 2013, 435, 502. [Google Scholar] [CrossRef]
- Perego, A.; Rosswog, S.; Cabezón, R.M.; Korobkin, O.; Käppeli, R.; Arcones, A.; Liebendörfer, M. Neutrino-driven winds from neutron star merger remnants. Mon. Not. R. Astron. Soc. 2014, 443, 3134–3156. [Google Scholar] [CrossRef]
- Siegel, D.M.; Ciolfi, R.; Rezzolla, L. Magnetically driven winds from differentially rotating neutron stars and X-ray afterglows of short gamma-ray bursts. Astrophys. J. 2014, 785, L6. [Google Scholar] [CrossRef]
- Just, O.; Bauswein, A.; Pulpillo, R.A.; Goriely, S.; Janka, H.T. Comprehensive nucleosynthesis analysis for ejecta of compact binary mergers. Mon. Not. R. Astron. Soc. 2015, 448, 541–567. [Google Scholar] [CrossRef]
- Rezzolla, L.; Kumar, P. A novel paradigm for short gamma-ray bursts with extended X-ray emission. Astrophys. J. 2015, 802, 95. [Google Scholar] [CrossRef]
- Ciolfi, R.; Siegel, D.M. Short gamma-ray bursts in the “time-reversal” scenario. Astrophys. J. 2015, 798, L36. [Google Scholar] [CrossRef]
- Siegel, D.M.; Metzger, B.D. Three-Dimensional General-Relativistic Magnetohydrodynamic Simulations of Remnant Accretion Disks from Neutron Star Mergers: Outflows and r-Process Nucleosynthesis. Phys. Rev. Lett. 2017, 119, 231102. [Google Scholar] [CrossRef] [PubMed]
- Kasen, D.; Metzger, B.; Barnes, J.; Quataert, E.; Ramirez-Ruiz, E. Origin of the heavy elements in binary neutron-star mergers from a gravitational wave event. Nature 2017. [Google Scholar] [CrossRef] [PubMed]
- Paczynski, B. Gamma-ray bursters at cosmological distances. Astrophys. J. 1986, 308, L43–L46. [Google Scholar] [CrossRef]
- Eichler, D.; Livio, M.; Piran, T.; Schramm, D.N. Nucleosynthesis, Neutrino Bursts and Gamma-Rays from Coalescing Neutron Stars. Nature 1989, 340, 126–128. [Google Scholar] [CrossRef]
- Van Eerten, E.T.H.; Ryan, G.; Ricci, R.; Burgess, J.M.; Wieringa, M.; Piro, L.; Cenko, S.B.; Sakamoto, T. A year in the life of GW170817: the rise and fall of a structured jet from a binary neutron star merger. arXiv 2018, arXiv:1808.06617. [Google Scholar]







| e | |||||||
|---|---|---|---|---|---|---|---|
| 1.365 | 1.527 | 0.18 | 11.0 | 378 | 2.705 | 8.324 |
| Name | n | ||||
|---|---|---|---|---|---|
| R1 | 4 | 192 | 64 | ||
| R2 | 4 | 288 | 96 | ||
| R3 | 4 | 384 | 128 | ||
| R4 | 4 | 480 | 160 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gieg, H.; Dietrich, T.; Ujevic, M. Simulating Binary Neutron Stars with Hybrid Equation of States: Gravitational Waves, Electromagnetic Signatures and Challenges for Numerical Relativity. Particles 2019, 2, 365-384. https://doi.org/10.3390/particles2030023
Gieg H, Dietrich T, Ujevic M. Simulating Binary Neutron Stars with Hybrid Equation of States: Gravitational Waves, Electromagnetic Signatures and Challenges for Numerical Relativity. Particles. 2019; 2(3):365-384. https://doi.org/10.3390/particles2030023
Chicago/Turabian StyleGieg, Henrique, Tim Dietrich, and Maximiliano Ujevic. 2019. "Simulating Binary Neutron Stars with Hybrid Equation of States: Gravitational Waves, Electromagnetic Signatures and Challenges for Numerical Relativity" Particles 2, no. 3: 365-384. https://doi.org/10.3390/particles2030023
APA StyleGieg, H., Dietrich, T., & Ujevic, M. (2019). Simulating Binary Neutron Stars with Hybrid Equation of States: Gravitational Waves, Electromagnetic Signatures and Challenges for Numerical Relativity. Particles, 2(3), 365-384. https://doi.org/10.3390/particles2030023





