Quantum Limit for the Emittance of Dirac Particles Carrying Orbital Angular Momentum
Abstract
:1. Introduction
2. On the Box Potential for Particles and Anti-Particles
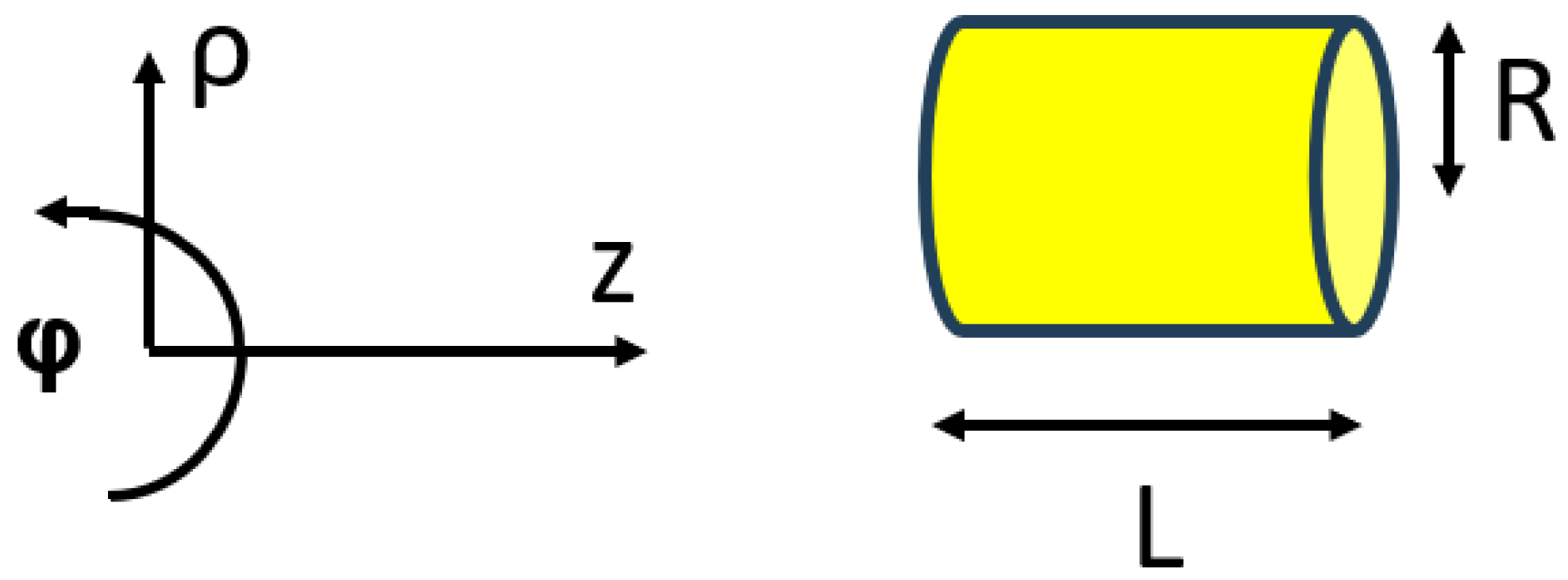
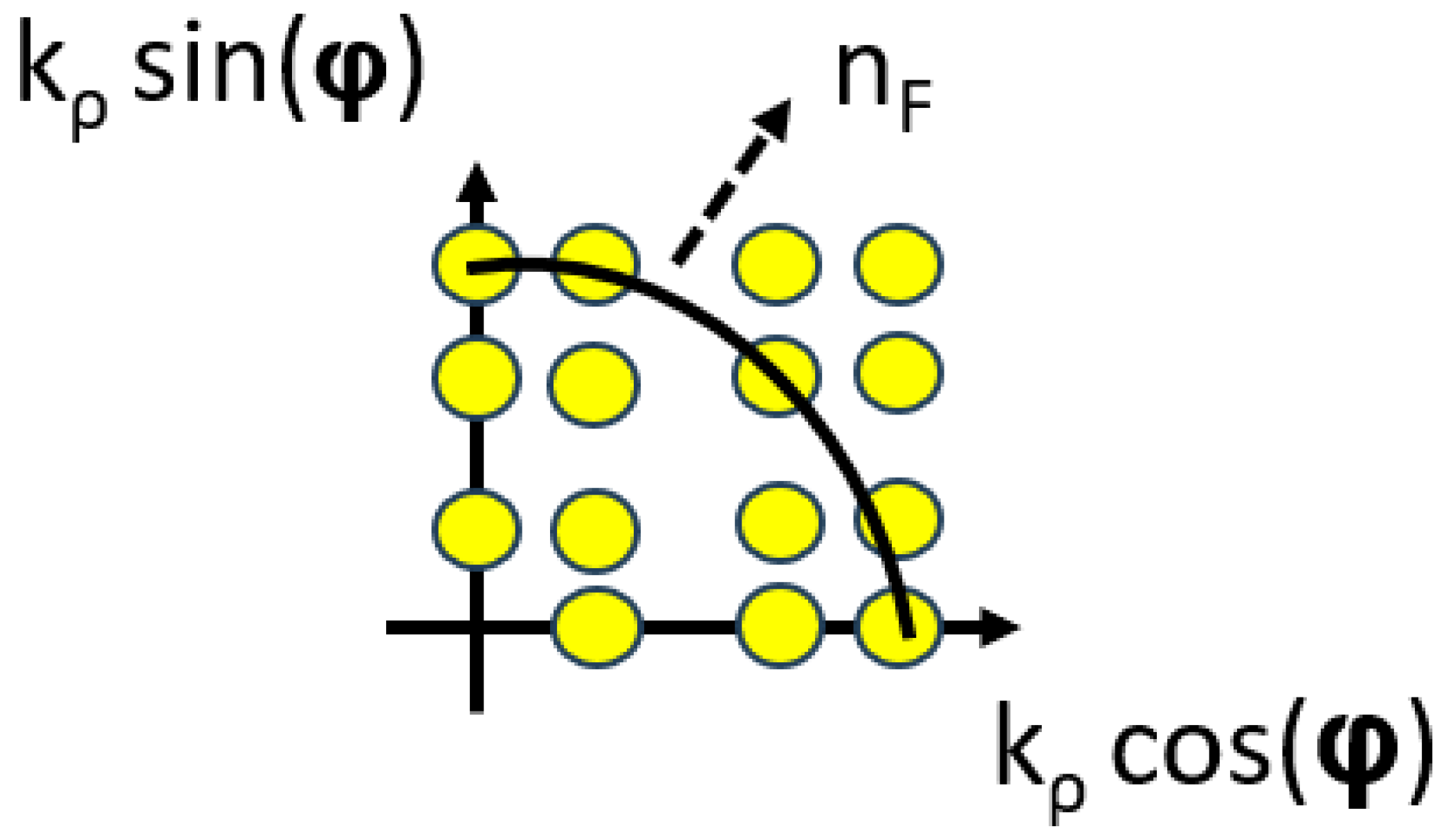
3. Relativistic Particle in a Cylindrical Box
4. Limit of a Relativistic Particle Beam
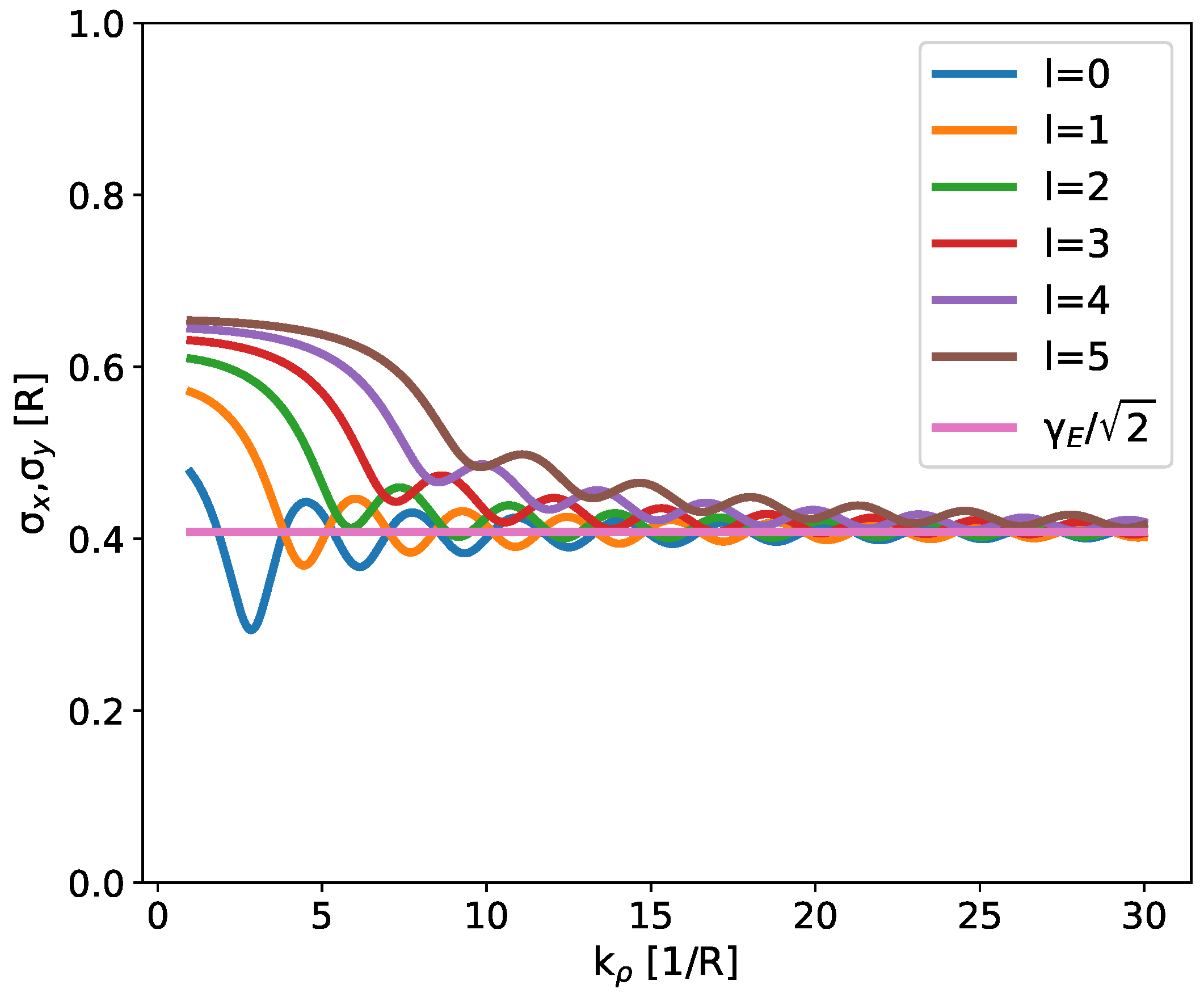
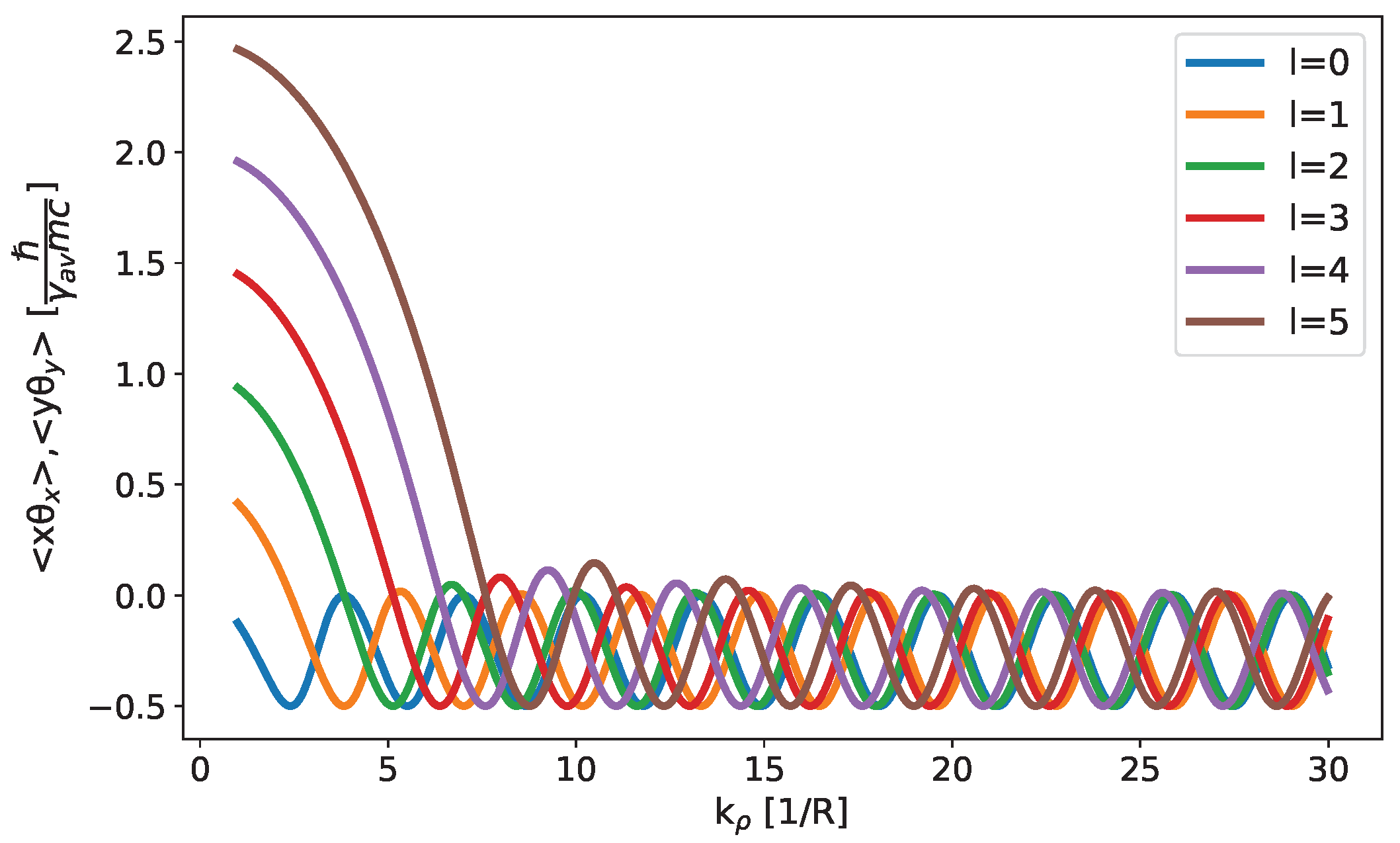
5. Rms Observables
6. Transverse Beam Emittance: The Quantum Limit
7. Role of the Transverse Temperature and Classical Limit
8. Particle Beams Carrying Orbital Angular Momentum
9. Single-Particle Emittance
10. Entropy
11. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Thomas, A.W. Chiral symmetry and the bag model: A new starting point for nuclear physics. In Advances in Nuclear Physics: Volume 13; Springer: Berlin/Heidelberg, Germany, 1984; pp. 1–137. [Google Scholar]
- Bhaduri, R. Models of the Nucleon: From Quarks to Soliton. In Vol. 22 of Lecture Notes and Supplements in Physics Addison-Wesley; Addison-Wesley: Redwood City, CA, USA, 1988. [Google Scholar]
- Alberto, P.; Fiolhais, C.; Gil, V. Relativistic particle in a box. Eur. J. Phys. 1996, 17, 19. [Google Scholar] [CrossRef]
- Alberto, P.; Das, S.; Vagenas, E.C. Relativistic particle in a three-dimensional box. Phys. Lett. A 2011, 375, 1436–1440. [Google Scholar] [CrossRef]
- Wiedemann, H. Particle Accelerator Physics; Springer Nature: Berlin, Germany, 2015. [Google Scholar]
- Adler, C.G. The relativistic one-dimensional square potential. Am. J. Phys. 1971, 39, 305–309. [Google Scholar] [CrossRef]
- Coutinho, F.A.B.; Nogami, Y.; Toyama, F. General aspects of the bound-state solutions of the one-dimensional Dirac equation. Am. J. Phys. 1988, 56, 904–907. [Google Scholar] [CrossRef]
- Greiner, W. Relativistic Quantum Mechanics; Springer: Berlin/Heidelberg, Germany, 2000; Volume 2. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; US Government Printing Office: Washington, DC, USA, 1968; Volume 55.
- Mikhailichenko, A. To the quantum limitations in beam physics. In Proceedings of the 1999 Particle Accelerator Conference (Cat. No. 99CH36366), New York, NY, USA, 29 March–2 April 1999; IEEE: Toulouse, France, 1999; Volume 4, pp. 2814–2816. [Google Scholar]
- Kabel, A.C. Quantum ground state and minimum emittance of a fermionic particle beam in a circular accelerator. In Quantum Aspects Of Beam Physics; World Scientific: London, UK, 2002; pp. 67–75. [Google Scholar]
- Burov, A.; Nagaitsev, S.; Shemyakin, A.; Derbenev, Y. Optical principles of beam transport for relativistic electron cooling. Phys. Rev. Spec. Top.-Accel. Beams 2000, 3, 094002. [Google Scholar] [CrossRef]
- Lawson, J.; Gluckstern, R.; Lapostolle, P.M. Emittance, entropy and information. Part. Accel. 1973, 5, 61–65. [Google Scholar]
- Sommerfeld, A. Zur elektronentheorie der metalle. Naturwissenschaften 1927, 15, 825–832. [Google Scholar] [CrossRef]

| l | |
|---|---|
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Curcio, A.; Cianchi, A.; Ferrario, M. Quantum Limit for the Emittance of Dirac Particles Carrying Orbital Angular Momentum. Particles 2024, 7, 264-274. https://doi.org/10.3390/particles7010015
Curcio A, Cianchi A, Ferrario M. Quantum Limit for the Emittance of Dirac Particles Carrying Orbital Angular Momentum. Particles. 2024; 7(1):264-274. https://doi.org/10.3390/particles7010015
Chicago/Turabian StyleCurcio, Alessandro, Alessandro Cianchi, and Massimo Ferrario. 2024. "Quantum Limit for the Emittance of Dirac Particles Carrying Orbital Angular Momentum" Particles 7, no. 1: 264-274. https://doi.org/10.3390/particles7010015
APA StyleCurcio, A., Cianchi, A., & Ferrario, M. (2024). Quantum Limit for the Emittance of Dirac Particles Carrying Orbital Angular Momentum. Particles, 7(1), 264-274. https://doi.org/10.3390/particles7010015








