Abstract
The present investigation explores the spatial distribution of Cooper pair density in graph-shaped arrays of Josephson junctions using a Ginzburg–Landau approach. We specifically investigate double-comb structures and compare their properties with linear arrays as reference systems. Our findings reveal that the peculiar connectivity of the double-comb structure leads to spatial gradients in the order parameter, which can be readily detected through measurements of Josephson critical currents. We present experimental results which indicate the specific dependence of the order parameter on the branches of the graphs and are evidence of the theoretical predictions.
1. Introduction
Josephson junctions and the systems or devices they can originate from have gathered noticeable attention in recent decades in the field of superconductivity [1,2,3,4,5,6]. The highly nonlinear internal dynamics of the junctions, their magnetic properties, and their intriguing potentials have originated research avenues and promising perspectives for both “point junctions” [7,8,9], namely junctions with physical dimensions smaller than the Josephson penetration depth [1,2,3,4,5,6], and “long” junctions, with at least one physical dimension larger than this characteristic parameter [10,11,12,13]. The investigation and the properties of Josephson potentials have also generated interest and a vast number of studies [14,15,16,17,18,19].
Within Josephson research, however, substantial efforts have been devoted to the understanding of the complex physics of arrays of junctions, both in two dimensions (2D), or planar space [20], and three dimensions (3D) [21]. Research on these arrays was also motivated by the rather successful operation of the quantum voltage standard, both in superconductor-isolator-superconductor (SIS) junctions’ [22,23,24] and in superconductor-normal-superconductor (SNS) junctions’ [25,26] operation modes. Nowadays, arrays of Josephson junctions and related voltage standard chips are being used for relevant implementations of high-precision metrology [27]. From a fundamental point of view, 2D arrays have served as a benchmark for testing solid-state phase transitions [28,29,30,31,32,33] and the coherent generation of microwave and millimeter-wave radiation [34,35,36,37,38,39,40,41]. Both the structure of polycrystalline high-temperature superconducting materials and the layered structure of single crystals of these materials have drawn much attention toward arrays of Josephson junctions for modeling intergrain or interlayer coupling [42] in view of specific applications [43,44].
In Ref. [45], the ability of an array of bosonic islands, linked by suitable potentials, to induce a Bose–Einstein condensation (BEC) effect was investigated. Concurrently, evidence was presented that a planar array of superconducting islands—housing zero-momentum Cooper pairs and connected via Josephson tunnel junctions—could also demonstrate the bosonic behavior of Cooper pairs, as initially proposed in Refs [46,47]. This issue has been further analyzed from a mathematical perspective by other researchers [48,49,50,51,52]. In Refs. [46,47,48,49,50,51,52] it was suggested that the BEC phenomenon could be observed in tree-like inhomogeneous graphs comprised of bosonic islands connected by suitable potentials. In this respect and for the sake of clarity, it is important to distinguish the BEC phenomenology discussed above from the BEC phase of a system undergoing a Bardeen-Cooper-Schrieffer (BCS)–BEC transition, which relates to the size of a Cooper pair as determined by the pairing interaction strength. The essence of Bose–Einstein condensation is the macroscopic occupation of the ground state by a system of non-interacting bosons at low temperatures. This phenomenon, fundamentally, does not imply the spatial localization of bosons in physical space. However, when one considers BEC on inhomogeneous graphs, an intriguing situation arises.
In such graphs, characterized by their non-uniform connectivity, the ground state of the single boson problem can indeed be exponentially localized around the node(s) with the highest degree of connectivity. These highly connected nodes effectively act as potential wells, attracting bosons to localize around them. This localization is not merely a spatial concentration but is intrinsically linked to a complicated interplay between phase coherence and the system’s topology. When extending this scenario to multiple bosons, the BEC phenomenon promotes the occupation of this energetically favorable, spatially localized ground state. Therefore, BEC in inhomogeneous graphs is not only a manifestation of bosons occupying the lowest energy state but also exhibits exponential localization at the node(s) with the highest connectivity. This dual aspect of BEC in such systems—both a quantum statistical phenomenon and a spatial localization due to the underlying graph topology—is exactly what we highlight in this paper.
Thus, it is essential to stress that the reported spatial localization of bosons on inhomogeneous graphs, while inherently tied to the network’s topology, is also accompanied by phase coherence due to its unique nature. This dual characteristic of localization and coherence firmly situates this study within the applicability region of a Ginzburg–Landau theory. Remarkably, the aforementioned spatial localization also applies to Cooper pairs, which are composite bosons obeying a modified algebra.
Since 2004, evidence has been piling up that in both double-comb structures [53,54,55] and in star-shaped structures [56], the effects predicted by the theories [46,47] could be qualitatively and quantitatively recorded in arrays of Josephson junctions. An explanation of the experimentally observed phenomena displaying anomalous distributions of Josephson currents in the arrays has been provided so far only in terms of the theories mentioned just above and no alternative models in terms of specific electromagnetic or thermodynamic effects have ever been provided or suggested.
Recently, it has been shown [57,58] that not only the Josephson critical currents of the arrays but even the energy gaps of the tunnel junctions forming the arrays could be conditioned by the peculiar shape of the graph. This was a somewhat surprising effect since it showed that the topology also influences the superconducting spectral gap of the whole network and thus its superconducting transition temperature. This phenomenon could not be predicted within the framework of BEC-biased theories [46,47] since the latter assume the existence of preformed bosons (Cooper pairs), so within the mentioned context, no prediction about the superconducting condensation temperature is available.
In order to account for the effects of inhomogeneous superconductivity such as those reported above, a De Gennes–Alexander model of granular superconductors was developed [59] and applied to star-shaped arrays of junctions. This approach, based on a discrete version of the Ginzburg–Landau (GL) theory [60,61,62], showed consistency with the previous BEC-based theoretical models and very good agreement with experimental results [63,64]. In the present paper, by using the same approach formulated in Ref. [59], we describe, for the first time, the spatial inhomogeneity of the Josephson critical currents of a double-comb-shaped array and compare the theoretical results with experimental data.
In close proximity to the phase transition temperature, the GL theory on graphs is mathematically equivalent to a single-particle eigenproblem in quantum mechanics [59]. The ground state of the equivalent problem leads us to estimate the critical temperature and the order parameter profile of a granular system at the phase transition. Thus, the linearized GL theory is based on the diagonalization of a “Hamiltonian” matrix, describing the connectivity of the granular system. Within this framework, the network critical temperature and the order parameter profile are determined by the ground state energy and its associated eigenstate. The minimum eigenvalue, of the Hamiltonian matrix, i.e., the ground state energy, is related to the transition temperature of the network () according to the following equation:
where represents the bulk critical temperature of the superconducting material used for synthetizing the islands forming the superconducting network and is the temperature-independent parameter of the GL theory.
The order parameter profile () and the ground state eigenvector ( are proportional, i.e.,
where the scale factor, , is determined by a free energy minimization procedure.
The GL theory predicts that the exponential localization of the order parameter, taking place in peculiar structures, is related to an enhancement in the network critical temperature. Actually, when the order parameter is localized, assumes negative values, implying an increase in the critical temperature of the network with respect to that of a single disconnected island. Regarding the applicability of the GL formulation, it is known that while the GL approach aligns closely with a BCS treatment near the transition temperature, its utility extends beyond this narrow range as an effective theory [59,60,61,62]. Employing a GL formulation beyond its validity regime provides a qualitatively accurate theoretical framework, albeit with expected quantitative discrepancies. In this context, our theory serves as an effective model, with the caveat that a microscopic approach would be necessary for further scrutiny. In line with this effective theory perspective, we assume the uniformity of the order parameter within each island (which is a rather reasonable assumption in view of the micrometric size of the superconducting islands), allowing a single order parameter value to represent the whole island. The observed order parameter inhomogeneity along the network stems from the Josephson coupling between adjacent islands, which modifies the nucleation conditions of the superconducting order parameter within any given island, contrasting sharply with the conditions experienced by isolated islands. These basic arguments represent the key points of the present investigation.
The paper is structured as follows. In Section 2, we apply the GL approach to a linear array of junctions serving as a reference system, while in Section 3, we apply the model to a double-comb structure. In Section 4, we link the order parameter profile, predicted by the theoretical model, to the Josephson critical currents and report the experimental results obtained on the Josephson junction arrays. In Section 5, conclusions and perspectives are given.
2. Linear Arrays
In this Section, we consider the properties of a plain array, which is used to introduce the theoretical model and the relevant notation in a plain context. Thus, let us consider a linear chain of N superconducting islands. The system is depicted in Figure 1, where squares represent the superconducting islands, while the straight gray crossed lines stand for “ideal” connections between the islands due to the Josephson coupling. In terms of network topology, each island, except those at the endpoints, is connected to two neighbors.
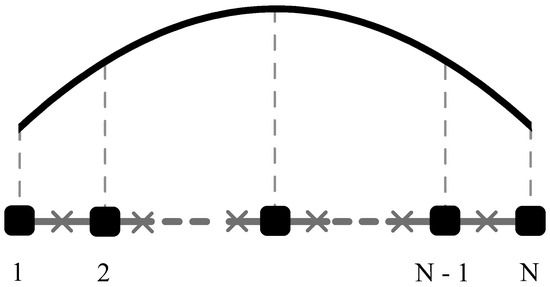
Figure 1.
Schematic picture of a linear chain. Black squares represent superconducting islands, while gray lines represent Josephson junctions that realize the Josephson coupling between islands. The black line represents the order parameter corresponding to the lowest energy eigenstate. See text for more details.
The eigenproblem induced by the Hamiltonian matrix of such a granular system can be written in the form:
where is the island’s index, E is the energy eigenvalue, and represents the onsite energy, while is related to the Josephson coupling between two neighbor islands. The eigenfunctions of the problem are , while the ground state, which is related to the order parameter profile at the phase transition, is obtained by setting the quantum number to .
The transition temperature of this network can be estimated through the ground state eigenvalue, of the eigenproblem given in Equation (1). Thus, the network critical temperature, , is (see [59] for details):
is lower than and depends on the system size. In the limit of a linear chain containing an infinite number of islands (), one observes that . Interestingly, by including the nonlinear terms in the theory, it is possible to demonstrate that the order parameter profile shows a tendency to become uniform along the array as the temperature is lowered below the critical temperature. Thus, one concludes that in a linear array, the Josephson critical currents of all the biased junctions coincide under the usual measuring conditions.
3. Double-Comb Networks
A double-comb network (see Figure 2), the main object of the present analysis, consists of a “horizontal” array called a backbone (the dark gray branch in Figure 2) connected to “vertical” arrays called fingers (the light gray branches in Figure 2). Each array, which is part of the system, is formed by a linear chain of superconducting islands connected by Josephson junctions. A single island located on the backbone is connected to four islands, two of which are also located on the backbone, and the other two are located on the fingers. The islands located on the fingers instead present only two connections. In the following analysis, we will assume a system not affected by structural disorder, i.e., made of a collection of identical islands and junctions.
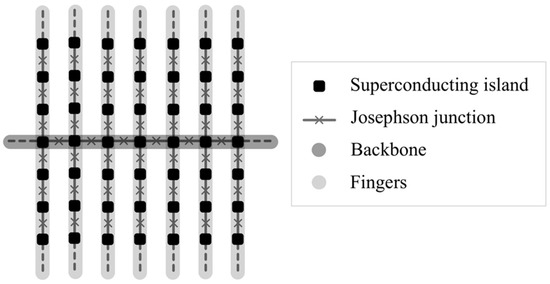
Figure 2.
Schematic picture of a double-comb array. Black squares represent superconducting islands, while gray crossed lines represent Josephson junctions, which are responsible for the Josephson coupling between islands.
The connectivity between islands represents the key point of the following analysis. The connectivity, however, does not change if the graph shown in Figure 2 is deformed into the shape of that presented in Figure 3, because the Hamiltonian matrix remains unaffected by the transformation. In view of the previous statements, the deformation preserves the physical properties of the network (i.e., the superconducting properties), while allowing for a more convenient labeling of the system islands.
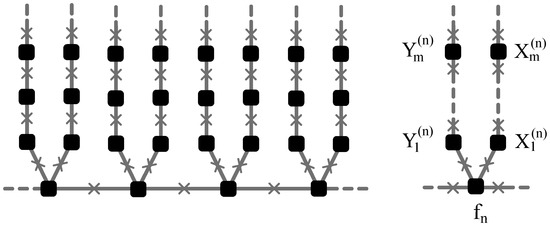
Figure 3.
A topologically-equivalent version of a double-comb network. Squares represent superconductive islands, while crosses represent Josephson junctions. See text for more details.
This paper analyzes the double-comb network in three different cases, depending on the number of islands forming the backbone and the fingers. Hereafter, we name the backbone’s order parameter and the fingers’ order parameters and , where the subscript index represents the n-th site of the backbone, while the subscript index represents the m-th site of the fingers.
3.1. Double Comb (Bf)
The first case, which we name “Bf”, is a double comb with an infinite number of islands on its backbone () and a finite number of islands on its fingers ().
Following Ref. [59], the extremal condition for the order parameter can be written as follows:
Since we expect a localized solution along the fingers, an expectation confirmed by the numerical analysis, we use the following ansatz for the order parameter profile:
where is a positive quantity, is a wave number, and the unknown parameters and are determined by using the boundary conditions: and . Network critical temperature is obtained by searching for the smallest eigenvalue of the Hamiltonian matrix, which depends on the number of islands, , contained along the fingers. Finite-size effects are negligible for , so, by setting , the network critical temperature is well approximated by the following relation:
Moreover, the order parameter profile (see Figure 4 for a graphic view) at the phase transition temperature is given by:
Figure 4.
The order parameter profile at the phase transition temperature for a double-comb “Bf”-type structure (an infinite number of islands for the backbone and a finite number of islands on the fingers), as obtained from Equation (6). One can see that the profile is constant along the backbone direction (left), while it decreases exponentially along the fingers’ direction (right).
3.2. Double Comb (bF)
The second case, which we name “bF”, is a double comb with a finite number of islands on its backbone () and an infinite number of islands along its fingers ().
Proceeding as in Section 3.1, the extremal condition for the order parameter profile can be written as follows:
We are looking for a localized solution along the fingers, and thus we use the following ansatz for the order parameter profile:
where is a positive parameter, while the boundary conditions and are used to fix the unknown quantities and . One can calculate the critical temperature of the network by finding the minimum eigenvalue of the Hamiltonian matrix, so that
Moreover, the order parameter profile at the phase transition takes the following form (see Figure 5 for a graphical view):
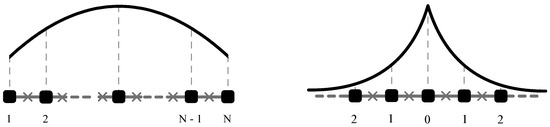
Figure 5.
The order parameter profile at the transition temperature for a double−comb array of the “bF” type (finite number of islands on the backbone and infinite number of islands for the finger), as obtained from Equation (10). The profile is sinusoidal along the backbone direction (left), while it decreases exponentially along the fingers’ direction (right).
3.3. Double Comb (BF)
The third case, which we name “BF”, is a double comb with an infinite number of islands on its backbone () and an infinite number of islands on its fingers ().
The extremal condition for the order parameter can be written as follows:
Searching for a localized solution along the fingers, we use the following ansatz for the order parameter profile:
where is a positive parameter to be determined by using the boundary conditions . According to Ref. [59], we calculate the critical temperature of the network by means of the smallest eigenvalue of the Hamiltonian matrix or, in an equivalent way, by taking the limit of ; accordingly:
while the order parameter profile takes the following form (see Figure 6 for a graphical view):
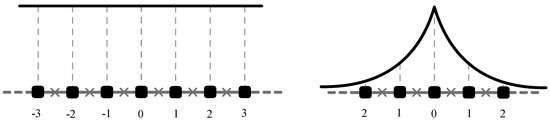
Figure 6.
The order parameter profile at the phase transition temperature for a double-comb array of the “BF” type (infinite number of islands for the backbone and infinite number of islands for the fingers), as obtained from Equation (14). One can see that the profile is constant along backbone direction (left), while it decreases exponentially along the fingers’ direction (right). Note that the profile on the fingers is essentially identical to that of the “bF” case shown in Figure 5.
4. Josephson Critical Currents Enhancement: Theory versus Experiments
So far, we have demonstrated that inhomogeneous superconductivity can be obtained and controlled in tree-like structures of superconducting islands coupled by Josephson weak links. In inhomogeneous superconductors, the network transition temperature is related to the spectral gap, while the space-dependent order parameter of the GL theory is related to the local value of the Cooper pair density. The above observation determines a rather subtle scenario. On one hand, the network transition temperature is proportional to the spectral gap, which is detectable by direct inspection of the current–voltage characteristics of a Josephson junction array. On the other hand, the local values of the order parameter have a direct influence on the Josephson critical currents. In particular, amplification phenomena of the Josephson critical currents are expected when the network topology constrains the Cooper pairs to be concentrated along the supercurrent path. In this way, differently from what is expected for homogeneous superconductors (with no space modulation of the order parameter), the Josephson critical currents and the spectral gap are related in a nontrivial manner.
In order to probe inhomogeneous superconductivity features, we show the relation between the Josephson critical current and the order parameter profile. Let us start by recalling the expression for the energy, of a Josephson junction. It is a phase-dependent quantity which can be obtained by taking into account the constitutive equations of the Josephson effect. Thus, the Josephson junction energy can be written as follows:
where is the magnetic flux quantum, h is the Planck constant, is the phase difference between the superconducting order parameters of the electrodes forming the junction, and represents the critical current.
Within a GL theory, the contribution to the free energy related to the coupling between two superconducting regions, described by the macroscopic order parameters and , is given by , where “c.c.” stands for complex conjugate. Thus, within a GL approach the Josephson junction energy takes the form:
A direct comparison between Equations (15) and (16) immediately implies that
Equation (17) shows that an enhancement in the Josephson critical current can be obtained in superconducting networks whose topology is able to induce a concentration of Cooper pairs along the supercurrent direction. This is exactly the case of the double-comb network, where the Cooper pairs are expected to be concentrated along the backbone array.
In order to perform an experimental test of the theoretical results, we measured the current–voltage characteristics of double-comb arrays, whose fabrication details have already been reported in Refs. [54,57]. Here, it is just worth mentioning that the double-comb arrays studied in this paper contain all-niobium junctions fabricated according to a trilayer technology [65,66,67,68]. A data acquisition system allowed us to record and analyze in a systematic way the current–voltage characteristics. The experimental technique consists of comparing the current–voltage characteristics of linear arrays embedded within a tree-like structure (e.g., the backbone array connected to the fingers) with those of a linear array (disconnected from the fingers but geometrically identical to the embedded array) used as a reference system.
Here, we focus on the statistical distribution of the Josephson critical currents forming the backbone of a double-comb array. The measured double-comb arrays contain a finite number of fingers departing from the backbone (100), while the finger arrays have a finite number of junctions on both sides of the backbone (50). Since the order parameter at the phase transition temperature shows a rapid decay along the finger direction (see Figure 5), we assume that our arrays belong to the “bF” class described in Section 3, i.e., arrays with a finite number of islands on the backbone and an infinite number of islands on the fingers.
The first and most striking piece of evidence of the difference between the Josephson critical current distributions on the backbone array embedded in the graph topology and its geometrical equivalent, namely its “reference” array, is shown in Figure 7. The data depicted in Figure 7 are derived from the current–voltage characteristics outlined in Ref. [64]. We partitioned the current axis into “bins,” specifically 0.3 μA for the backbone array and 0.2 μA for the reference array. Subsequently, we tallied the number of points with critical currents falling within each designated bin. The inverse of this count provides us with the density function.
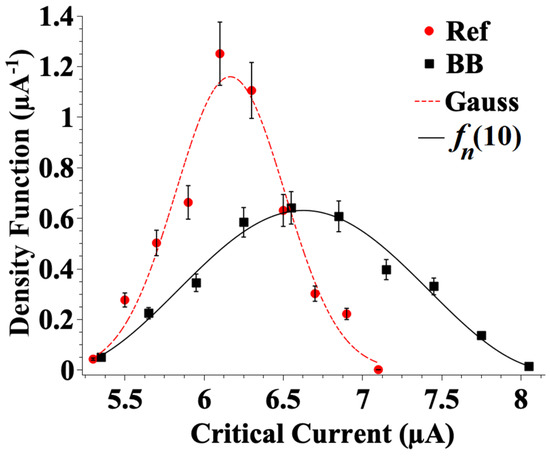
Figure 7.
Experimental distribution of the Josephson critical currents of an “embedded” backbone (BB) array (solid squares and continuous line) and those of its geometrically equivalent or reference (Ref) array (solid circles and dashed line (Gaussian function)). One can see the noticeable difference in the distribution in the current interval where we map the density function. The data are taken from Ref. [64].
One can see that the critical currents of the reference array form a more peaked distribution with respect to that of the backbone. This result follows what we expect since the effect of the fingers is to condition the critical currents along the whole backbone, generating a wider spread of current values.
In Figure 7, the line through the data of the reference array is a Gaussian function, while that between the data of the backbone follows from a statistical distribution originating from function fn of Equation (10). Figure 7 well demonstrates that the specific connectivity strongly influences the distribution of currents on the backbone array and a good enough agreement between the distribution arising from the GL and the backbone array data. It is worth noting that, in order to perform the fit (lines) to the data, the linear transformation, was applied to the argument of the function fn of Equation (10) (and to the Gaussian function argument) in order to go from the Ic current bins to the position variable on the horizontal axis. Here, a and b are, respectively, the minimum and maximum values of the current interval. The physical meaning of the black curve providing a smooth interpolation of the experimental data is that the count of the Josephson critical currents of the array is higher around the center of the current interval (5–8 μA), given by the lowest and highest currents of the array.
Now, using the linear transformation, , applied to the values shown in Figure 7 (DF is the density function) and setting the argument of the function fn of Equation (10) in terms of position (n, junction number), we obtain, for the backbone array, the corresponding curve in Figure 8a. Here again we see that a rather smooth fit is obtained and that the maximum of the current is obtained around the center of the array, as we should expect from the theoretical predictions.
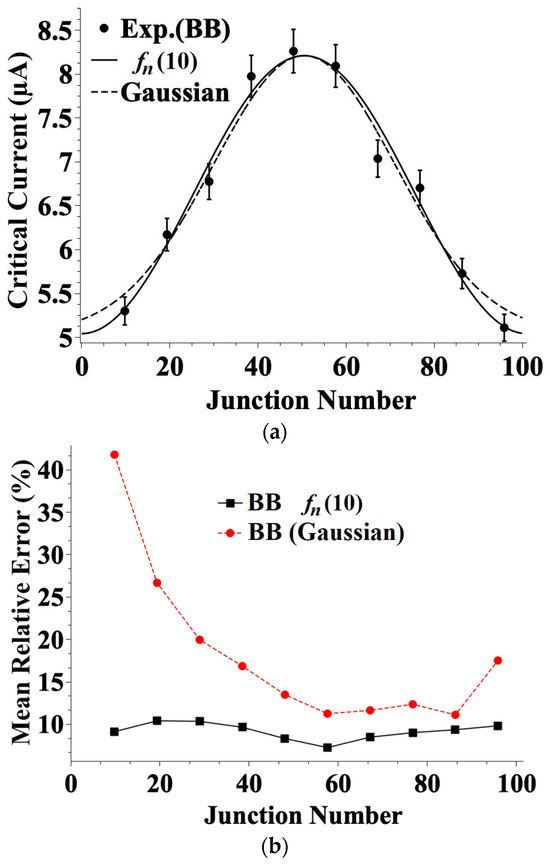
Figure 8.
(a) Experimental distribution of the Josephson critical currents between the islands of the backbone (BB) array for data from Ref. [64]. The continuous line is what we obtain by squaring function fn in Equation (10) and by adding a constant value mimicking the effect of background superconductivity. The dashed line is what one could expect from a Gaussian distribution. (b) A comparison of the discrepancies between experimental data and theory obtained for the experimental data and the two curves shown in (a). The dashed line and solid circles show the Gaussian distribution, while the solid squares and solid curve show the distribution originating from function fn in Equation (10).
It is worth noting that the distribution was symmetrical, as expected from function fn of Equation (10) and Figure 5, but even when attempting a fit with a Gaussian density, one obtains a reasonable agreement, as one can see in Figure 8a (the dashed curve). Nevertheless, in Figure 8b, one can see that the progressive mean of the discrepancy between the data and the “sinusoidal” fit based on function fn of Equation (10) stays, for all points, below 10%, whereas the progressive mean of the discrepancy obtained with the Gaussian fit is always above 10%, reaching a maximum of 40%. In Figure 8a, we used the progressive mean of the discrepancies in order to smooth out the dependencies; the lines in Figure 8b just guide the eyes.
It is worth noting that, for the data in Figure 7 and Figure 8, we bias the arrays in series in a four-probe configuration and have access to the voltage developed across them only at the end of the series connection, and therefore it is not possible to attribute a specific current to a specific junction between the islands. We have assumed earlier [63,64] that the junctions carrying the highest Josephson critical currents are those located toward the center of the array. Now Figure 7 and Figure 8 show that this assumption was reasonable since a specific functional form gives a quite good account of the behavior of the experimental data.
5. Conclusions
Over the past two decades, evidence that the Josephson critical currents and the gap energy (and thus the transition temperatures) in graph-shaped arrays of superconducting islands are conditioned by the network topology has been reported in several papers [53,54,55,56,57,58]. In the present study, we have demonstrated that a Ginzburg–Landau approach applied to double-comb arrays of junctions shows good agreement with the experimental data. Interestingly, the GL approach, in accordance with models based on a BEC scenario, predicts Cooper pair condensation driven by network connectivity. From an experimental viewpoint, the substantial differences observed between the arrays embedded in the comb structures and their geometrical equivalents (i.e., the reference arrays) provide stunning evidence of the role played by the network topology in superconductivity and, in general, in solid-state structures. The present paper has given an account, based on GL formalism, of the presumed earlier assumption concerning charge carriers’ spatial distribution in graph arrays [63,64]. In particular, the observed effects are suggestive of a nontrivial interplay between the macroscopic long-range quantum coherence and the network topology. Such effects are captured by any level of theoretical description, from a GL formulation [59,60,61,62] to more microscopic treatments [69,70], so they certainly deserve further experimental and theoretical investigations.
Author Contributions
Methodology, M.C.; software, R.B.; formal analysis, F.R.; investigation, E.T.; resources, V.M.; data curation, G.S.; writing—original draft, M.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We dedicate this endeavor to the memory of Francesco Saverio (Franco) Persico, whose high scientific profile, culture, and education have been appreciated over the years in academic and personal environments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Solymar, L. Superconductive Tunneling and Applications; John Wiley & Sons, Inc.: London, UK, 1972; Available online: https://archive.org/details/superconductivet0000soly/ (accessed on 1 March 2024).
- Kulik, I.O.; Yanson, I.K. The Josephson Effect in Superconductive Tunneling Structures; Israel Program for Scientific Translations: Jerusalem, Israel, 1972. [Google Scholar]
- Barone, A.; Paternò, G. Physics and Applications of the Josephson Effect; John Wiley & Sons, Inc.: New York, NY, USA, 1982. [Google Scholar] [CrossRef]
- Likharev, K.K. Dynamics of Josephson Junctions and Circuits; CRC Press/Taylor & Francis Group: London, UK, 1986; Available online: https://www.taylorfrancis.com/books/mono/10.1201/9781315141572/dynamics-josephson-junctions-circuits-konstantin-likharev (accessed on 1 March 2024).
- Tinkham, M. Introduction to Superconductivity; McGraw-Hill, Inc.: New York, NY, USA, 1996; Available online: https://pdfcoffee.com/introduction-to-superconductivity-by-michael-tinkham-2nd-edition-pdf-free.html (accessed on 1 March 2024).
- Van Duzer, T.; Turner, C.W. Principles of Superconducting Devices and Circuits; Prentice-Hall: Englewood Cliffs, NJ, USA, 1999. [Google Scholar]
- Huberman, B.A.; Crutchfield, J.P.; Packard, N.H. Noise phenomena in Josephson junctions. Appl. Phys. Lett. 1980, 37, 750–752. [Google Scholar] [CrossRef]
- Pedersen, N.F.; Davidson, A. Chaos and noise rise in Josephson junctions. Appl. Phys. Lett. 1981, 39, 830–832. [Google Scholar] [CrossRef]
- Kautz, R.L.; Monaco, R. Survey of chaos in the rf-biased Josephson junction. J. Appl. Phys. 1985, 57, 875–889. [Google Scholar] [CrossRef]
- McLaughlin, D.W.; Scott, A.C. Perturbation analysis of fluxon dynamics. Phys. Rev. A 1978, 18, 1652–1680. [Google Scholar] [CrossRef]
- Parmentier, R.D. Fluxons in long Josephson junctions. In Solitons in Action; Lonngren, K., Scott, A., Eds.; Academic Press, Inc.: New York, NY, USA, 1978; pp. 173–199. [Google Scholar] [CrossRef]
- Pedersen, N.F. Solitons in Josephson transmission lines. Mod. Probl. Condens. Matter Sci. 1986, 17, 469–501. [Google Scholar]
- Ustinov, A.V. Solitons in Josephson junctions. Phys. D Nonlin. Phenom. 1998, 123, 315–329. [Google Scholar] [CrossRef]
- Kurkijarvi, J. Intrinsic fluctuations in a superconducting ring closed with a Josephson junction. Phys. Rev. B 1972, 6, 832–835. [Google Scholar] [CrossRef]
- Fulton, T.A.; Dunkleberger, L.N. Lifetime of the zero-voltage state in Josephson tunnel junctions. Phys. Rev. B 1974, 9, 4760–4768. [Google Scholar] [CrossRef]
- Büttiker, M.; Harris, E.P.; Landauer, R. Thermal activation in extremely underdamped Josephson-junction circuits. Phys. Rev. B 1983, 28, 1268–1275. [Google Scholar] [CrossRef]
- Silvestrini, P.; Liengme, O.L.; Gray, K. Current distributions of thermal switching in extremely underdamped Josephson junctions. Phys. Rev. B 1988, 37, 1525–1531. [Google Scholar] [CrossRef] [PubMed]
- Silvestrini, P.; Palmieri, V.G.; Ruggiero, B.; Russo, M. Observation of energy levels quantization in underdamped Josephson junctions above the classical-quantum regime crossover temperature. Phys. Rev. Lett. 1997, 79, 3046–3049. [Google Scholar] [CrossRef]
- Oelsner, G.; Revin, L.S.; Il’ichev, E.; Pankratov, A.L.; Meyer, H.-G.; Grönberg, L.; Hassel, J.; Kuzmin, L.S. Underdamped Josephson junction as a switching current detector. Appl. Phys. Lett. 2013, 103, 142605. [Google Scholar] [CrossRef]
- Fazio, R.; van der Zant, H. Quantum phase transitions and vortex dynamics in superconducting networks. Phys. Rep. 2001, 355, 235–334. [Google Scholar] [CrossRef]
- S Sakai, S.; Ustinov, A.V.; Kohlstedt, H.; Petraglia, A.; Pedersen, N.F. Theory and experiment on electromagnetic-wave-propagation velocities in stacked superconducting tunnel structures. Phys. Rev. B 1994, 50, 12905–12914. [Google Scholar] [CrossRef] [PubMed]
- Niemeyer, J.; Hinken, J.H.; Kautz, R.L. Microwave-induced constant-voltage steps at one volt from a series array of Josephson junctions. Appl. Phys. Lett. 1984, 45, 478–480. [Google Scholar] [CrossRef]
- Pöpel, R.; Niemeyer, J.; Fromknecht, R.; Meier, W.; Grimm, L. 1- and 10-V series array Josephson voltage standards in Nb/Al2O3/Nb technology. J. Appl. Phys. 1990, 68, 4294–4303. [Google Scholar] [CrossRef]
- Lloyd, F.L.; Hamilton, C.A.; Beall, J.A.; Go, D.; Ono, R.H.; Harris, R.E. A Josephson array voltage standard at 10 V. IEEE Electr. Dev. Lett. 1987, 8, 449–450. [Google Scholar] [CrossRef]
- Benz, S.P.; Hamilton, C.A. Application of the Josephson effect to voltage metrology. Proc. IEEE 2004, 92, 1617–1629. [Google Scholar] [CrossRef]
- Schulze, H.; Behr, R.; Müller, F.; Niemeyer, J. Nb/Al/AlOx/AlOx/Al/Nb Josephson junctions for programmable voltage standards. Appl. Phys. Lett. 1998, 73, 996–998. [Google Scholar] [CrossRef]
- Bauer, S.; Behr, R.; Herick, J.; Kieler, O.; Kraus, M.; Tian, H.; Pimsut, Y.; Palafox, L. Josephson voltage standards as toolkit for precision metrological applications at PTB. Meas. Sci. Technol. 2023, 34, 032001. [Google Scholar] [CrossRef]
- Kosterlitz, J.M.; Thouless, D.J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C Solid State Phys. 1973, 6, 1181–1203. [Google Scholar] [CrossRef]
- Beasley, M.R.; Mooij, J.E.; Orlando, T.P. Possibility of vortex-antivortex pair dissociation in two-dimensional superconductors. Phys. Rev. Lett. 1979, 42, 1165–1168. [Google Scholar] [CrossRef]
- Resnick, D.J.; Garland, J.C.; Boyd, J.T.; Shoemaker, S.; Newrock, R.S. Kosterlitz–Thouless transition in proximity-coupled superconducting arrays. Phys. Rev. Lett. 1981, 47, 1542–1545. [Google Scholar] [CrossRef]
- Lobb, C.J.; Abraham, D.W.; Tinkham, M. Theoretical interpretation of resistive transition data from arrays of superconducting weak links. Phys. Rev. B 1983, 27, 150–157. [Google Scholar] [CrossRef]
- Benz, S.O.; Rzchowski, M.S.; Tinkham, M.; Lobb, C.J. Critical currents in frustrated two-dimensional Josephson arrays. Phys. Rev. B 1990, 42, 6165–6171. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.D.; Delsing, P.; Haviland, D.B.; Harada, Y.; Claeson, T. Flux flow and vortex tunneling in two-dimensional arrays of small Josephson junctions. Phys. Rev. B 1996, 54, 9449–9457. [Google Scholar] [CrossRef] [PubMed]
- Monaco, R.; Pagano, S.; Costabile, G. Superradiant emission from an array of long Josephson junctions. Phys. Lett. A 1988, 131, 122–124. [Google Scholar] [CrossRef]
- Pagano, S.; Monaco, R.; Costabile, G. Microwave oscillator using arrays of long Josephson junctions. IEEE Trans. Magn. 1989, 25, 1080–1083. [Google Scholar] [CrossRef]
- Monaco, R.; Grønbech-Jensen, N.; Parmentier, R.D. Self-locking of fluxon oscillations in series arrays of niobium Josephson tunnel junctions coupled to a linear resonator. Phys. Lett. A 1990, 151, 195–201. [Google Scholar] [CrossRef]
- Cirillo, M.; Modena, I.; Santucci, F.; Carelli, P.; Leoni, R. Coherence of Josephson soliton oscillators in the millimeter wave range. Phys. Lett. A 1992, 167, 175–178. [Google Scholar] [CrossRef]
- Ottaviani, I.; Cirillo, M.; Lucci, M.; Merlo, V.; Salvato, M.; Castellano, M.G.; Torrioli, G.; Mueller, F.; Weimann, T. Collective cavity mode excitations in arrays of Josephson junctions. Phys. Rev. B 2009, 80, 174518. [Google Scholar] [CrossRef]
- Benz, S.P.; Booi, P.A.A. High-frequency oscillators using phase-locked arrays of Josephson unctions. IEEE Trans. Ulrason. Ferroelectr. Freq. Control 1995, 42, 964–966. [Google Scholar] [CrossRef][Green Version]
- Jain, A.K.; Likharev, K.K.; Lukens, J.E.; Sauvageau, J.E. Mutual phase-locking in Josephson junction arrays. Phys. Rep. 1984, 109, 309–426. [Google Scholar] [CrossRef]
- Barbara, P.; Cawthorne, A.B.; Shitov, S.V.; Lobb, C.J. Stimulated emission and amplification in Josephson junction arrays. Phys. Rev. Lett. 1999, 82, 1963–1966. [Google Scholar] [CrossRef]
- Hott, R.; Kleiner, R.; Wolf, T.; Zwicknagl, G. Superconducting materials—A topical overview. In Frontiers in Superconducting Materials; Narlikar, A.V., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 1–69. [Google Scholar] [CrossRef]
- Ozyuzer, L.; Koshelev, A.E.; Kurter, C.; Gopalsami, N.; Li, Q.; Tachiki, M.; Kadowaki, K.; Yamamoto, T.; Minami, H.; Yamaguchi, H.; et al. Emission of coherent THz radiation from superconductors. Science 2007, 318, 1291–1293. [Google Scholar] [CrossRef]
- Cassinese, A.; Barra, M.; Ciccognani, W.; Cirillo, M.; De Dominicis, M.; Limiti, E.; Prigiobbo, A.; Russo, R.; Vaglio, R. Miniaturized superconducting filter realized by using dual-mode and stepped resonators. IEEE Transact. Microw. Theory Tech. 2004, 52, 97–104. [Google Scholar] [CrossRef]
- Brunelli, I.; Giusiano, G.; Mancini, F.P.; Sodano, P.; Trombettoni, A. Topology-induced spatial Bose-Einstein condensation for bosons on star-shaped optical networks. J. Phys. B At. Mol. Opt. 2004, 37, S275–S286. [Google Scholar] [CrossRef]
- Burioni, R.; Cassi, D.; Meccoli, I.; Rasetti, M.; Regina, S.; Sodano, P.; Vezzani, A. Bose-Einstein condensation in inhomogeneous Josephson arrays. Europhys. Lett. (EPL) 2000, 52, 251–256. [Google Scholar] [CrossRef]
- Buonsante, P.; Burioni, R.; Cassi, D.; Penna, V.; Vezzani, A. Topology-induced confined superfluidity in inhomogeneous arrays. Phys. Rev. B 2004, 70, 224510. [Google Scholar] [CrossRef]
- Fidaleo, F.; Guido, D.; Isola, T. Bose-Einstein condensation on inhomogeneous amenable graphs. Infin. Dimens. Anal. Quant. Probab. Relat. Top. 2011, 14, 149–197. [Google Scholar] [CrossRef]
- Fidaleo, F. Harmonic analysis on inhomogeneous amenable networks and the Bose-Einstein condensation. J. Stat. Phys. 2015, 160, 715–759. [Google Scholar] [CrossRef]
- Matsui, T. BEC of free bosons on networks. Infin. Dimens. Anal. Quant. Probab. Relat. Top. 2006, 9, 1–26. [Google Scholar] [CrossRef]
- Adami, R.; Serra, E.; Tilli, P. Negative energy ground states for the L2-critical NLSE on metric graphs. Commun. Math. Phys. 2017, 352, 387–406. [Google Scholar] [CrossRef]
- Lyra, M.L.; de Moura, F.A.B.F.; de Oliveira, I.N.; Serva, M. Bose-Einstein condensation in diamond hierarchical lattices. Phys. Rev. E 2014, 89, 052133. [Google Scholar] [CrossRef] [PubMed]
- Cirillo, M.; Merlo, V.; Russo, R.; Castellano, M.G.; Cosmelli, C.; Trombettoni, A.; Sodano, P. Spatial Bose-Einstein condensation in Josephson junctions arrays. In Quantum Computation in Solid State Systems; Ruggiero, B., Delsing, P., Granata, C., Pashkin, Y., Silvestrini, P., Eds.; Springer: New York, NY, USA, 2006; pp. 147–153. [Google Scholar] [CrossRef]
- Silvestrini, P.; Russo, R.; Corato, V.; Ruggiero, B.; Granata, C.; Rombetto, S.; Russo, M.; Cirillo, M.; Trombettoni, A.; Sodano, P. Topology-induced critical current enhancement in Josephson networks. Phys. Lett. A 2007, 370, 499–503. [Google Scholar] [CrossRef][Green Version]
- Ottaviani, I.; Lucci, M.; Menditto, R.; Merlo, V.; Salvato, M.; Cirillo, M.; Müller, F.; Weimann, T.; Castellano, M.G.; Chiarello, F.; et al. Characterization of anomalous pair currents in Josephson junction networks. J. Phys. Condens. Matter 2014, 26, 215701. [Google Scholar] [CrossRef] [PubMed]
- Lorenzo, M.; Lucci, M.; Merlo, V.; Ottaviani, I.; Salvato, M.; Cirillo, M.; Torrioli, G. On Bose-Einstein condensation in star shaped Josephson arrays. Phys. Lett. A 2014, 378, 655–658. [Google Scholar] [CrossRef]
- Lucci, M.; Cassi, D.; Merlo, V.; Russo, R.; Salina, G.; Cirillo, M. Conditioning of superconductive properties in graph-shaped reticles. Sci. Rep. 2020, 10, 10222. [Google Scholar] [CrossRef] [PubMed]
- Lucci, M.; Cassi, D.; Merlo, V.; Russo, R.; Salina, G.; Cirillo, M. Josephson currents and gap enhancement in graph arrays of superconductive islands. Entropy 2021, 23, 811. [Google Scholar] [CrossRef] [PubMed]
- Romeo, F. Order parameter focalization and critical temperature enhancement in synthetic networks of superconducting islands. J. Phys. Condens. Matter 2020, 33, 04540. [Google Scholar] [CrossRef] [PubMed]
- De Gennes, P.G. Superconductivity of Metals and Alloys; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar] [CrossRef]
- Tilley, D.R.; Tilley, J. Superfluidity and Superconductivity; IOP Publishing Ltd.: Bristol, UK, 1990. [Google Scholar] [CrossRef]
- Berger, J.; Rubinstein, J. Connectivity and Superconductivity; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Lucci, M.; Campanari, V.; Cassi, D.; Merlo, V.; Romeo, F.; Salina, G.; Cirillo, M. Quantum coherence in loopless superconductive networks. Entropy 2022, 24, 1690. [Google Scholar] [CrossRef] [PubMed]
- Bizzi, R.; Campanari, V.; Cassi, D.; Merlo, V.; Romeo, F.; Salina, G.; Cirillo, M. Evidence of long range coherence in superconducting networks. IEEE Transact. Appl. Supercond. 2023, 33, 1800106. [Google Scholar] [CrossRef]
- Gurvitch, M.; Washington, M.A.; Huggins, H.A. High quality refractory Josephson tunnel junctions utilizing thin aluminum layers. Appl. Phys. Lett. 1983, 42, 472–474. [Google Scholar] [CrossRef]
- Inoue, A.; Kotani, S.; Imamura, T.; Hasuo, S. Niobium based Josephson circuit technology. Appl. Supercond. 1993, 1, 1863–1877. [Google Scholar] [CrossRef]
- Yohannes, D.; Kirichenko, A.; Sarwana, S.; Tolpygo, S.K. Parametric testing of HYPRES superconducting integrated circuit fabrication processes. IEEE Transact. Appl. Supercond. 2007, 17, 181–186. [Google Scholar] [CrossRef]
- SEEQC. Chip Fabrication. Available online: https://seeqc.com/chip-foundry-services/chip-fabrication (accessed on 1 March 2024).
- Romeo, F.; De Luca, R. Cooper pairs localization in tree-like networks of superconducting islands. Eur. Phys. J. Plus. 2022, 137, 726. [Google Scholar] [CrossRef]
- Romeo, F. On the Bardeen–Cooper–Schrieffer interaction in quantum graphs. Eur. Phys. J. Plus 2023, 138, 463. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).