Exploring Stresses in Mandibular Jawbone during Implant Insertion: A Three-Dimensional Explicit Dynamic Analysis
Abstract
:1. Introduction
2. Materials and Methods
3. Results
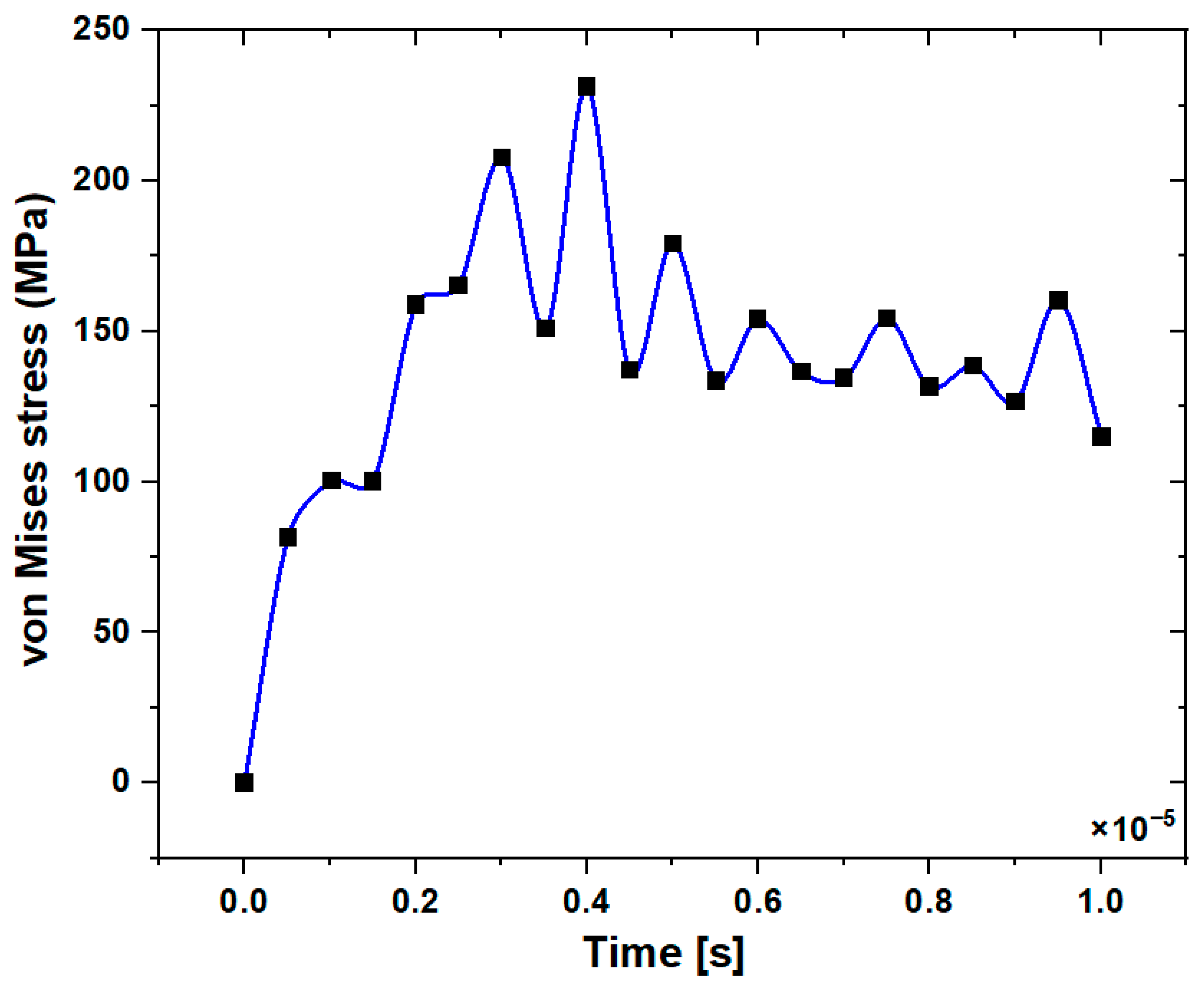
3.1. Stress Distribution in the Jawbone
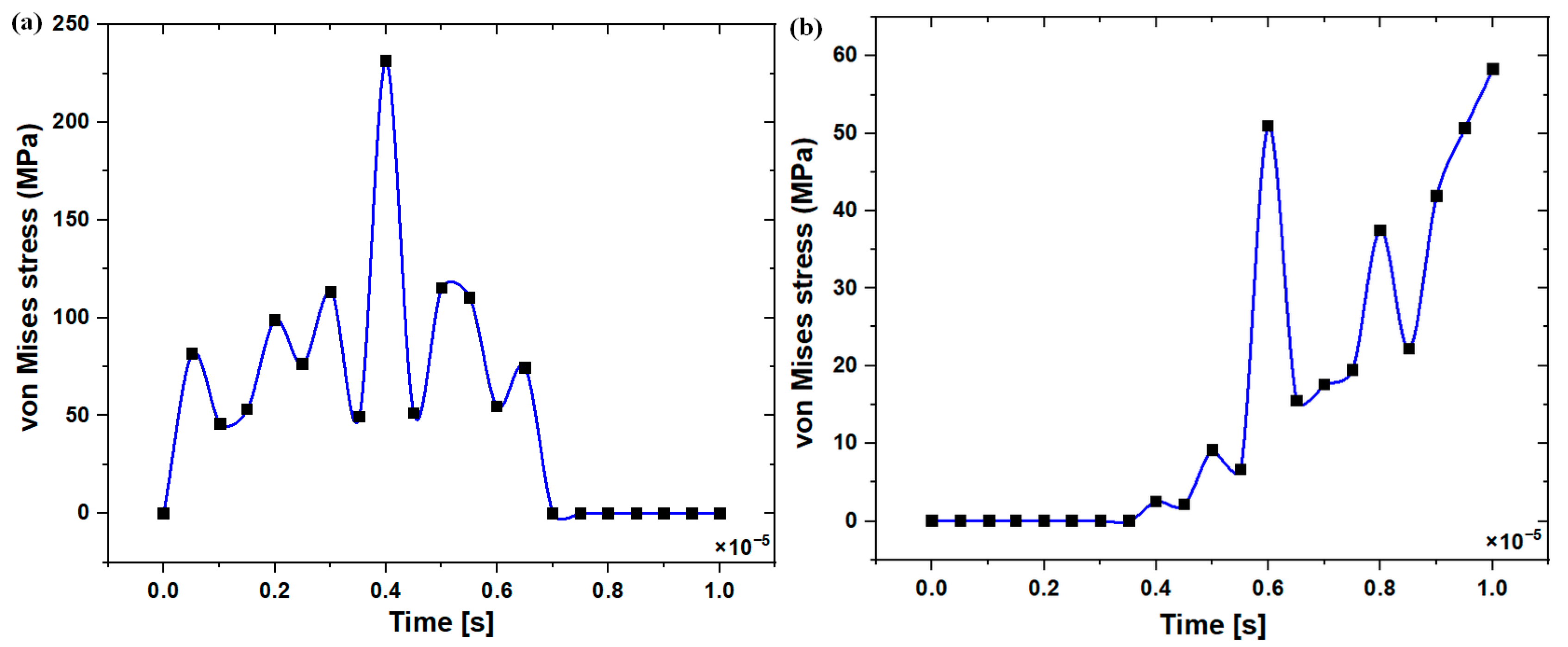
3.2. Stress Distribution at the Upper and Lower Edge of the Pre-Drilled Hole
3.3. Stress Distribution at the Surface Area of the Pre-Drilled Site during the Implant Insertion
4. Discussion
Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Matos, G.R.M. Surface Roughness of Dental Implant and Osseointegration. J. Maxillofac. Oral Surg. 2021, 20, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Smeets, R.; Stadlinger, B.; Schwarz, F.; Beck-Broichsitter, B.; Jung, O.; Precht, C.; Kloss, F.; Gröbe, A.; Heiland, M.; Ebker, T. Impact of Dental Implant Surface Modifications on Osseointegration. Biomed. Res. Int. 2016, 2016, 6285620. [Google Scholar] [CrossRef]
- Rittel, D.; Dorogoy, A.; Shemtov-Yona, K. Modeling the effect of osseointegration on dental implant pullout and torque removal tests. Clin. Implant Dent. Relat. Res. 2018, 20, 683–691. [Google Scholar] [CrossRef] [PubMed]
- Yi, Y.A.; Park, Y.B.; Choi, H.; Lee, K.W.; Kim, S.J.; Kim, K.M.; Oh, S.; Shim, J.S. The Evaluation of Osseointegration of Dental Implant Surface with Different Size of TiO2 Nanotube in Rats. J. Nanomater. 2015, 2015, 581713. [Google Scholar] [CrossRef]
- Rosa, C.D.; Bento, V.A.; Duarte, N.D.; Sayeg, J.M.; Santos, T.J.; Pellizzer, E.P. Do dental implants installed in different types of bone (I, II, III, IV) have different success rates? A systematic review and meta-analysis. Saudi Dent. J. 2023, in press. [Google Scholar] [CrossRef]
- Olmedo-Gaya, M.V.; Romero-Olid, M.N.; Ocaña-Peinado, F.M.; Vallecillo-Rivas, M.; Vallecillo, C.; Reyes-Botella, C. Influence of different surgical techniques on primary implant stability in the posterior maxilla: A randomized controlled clinical trial. Clin. Oral Investig. 2023, 27, 3499–3508. [Google Scholar] [CrossRef]
- Huang, Y.M.; Chou, I.-C.; Jiang, C.-P.; Wu, Y.-S.; Lee, S.-Y. Finite Element Analysis of Dental Implant Neck Effects on Primary Stability and Osseointegration in a Type IV Bone Mandible. Biomed. Mater. Eng. 2014, 24, 1407–1415. [Google Scholar] [CrossRef] [PubMed]
- Paracchini, L.; Barbieri, C.; Redaelli, M.; Di Croce, D.; Vincenzi, C.; Guarnieri, R. Finite Element Analysis of a New Dental Implant Design Optimized for the Desirable Stress Distribution in the Surrounding Bone Region. Prosthesis 2020, 2, 225–236. [Google Scholar] [CrossRef]
- Cicciù, M.; Cervino, G.; Terranova, A.; Risitano, G.; Raffaele, M.; Cucinotta, F.; Santonocito, D.; Fiorillo, L. Prosthetic and mechanical parameters of the facial bone under the load of different dental implant shapes: A parametric study. Adv. Surg. Med. Spec. 2019, 1, 41–53. [Google Scholar] [CrossRef]
- Udomsawat, C.; Rungsiyakull, P.; Rungsiyakull, C.; Khongkhunthian, P. Comparative study of stress characteristics in surrounding bone during insertion of dental implants of three different thread designs: A three-dimensional dynamic finite element study. Clin. Exp. Dent. Res. 2019, 5, 26–37. [Google Scholar] [CrossRef]
- Juneja, S.; Miranda, G.; Eram, A.; Shetty, N.; Chethan, K.N.; Keni, L.G. Investigating the Influence of All-Ceramic Prosthetic Materials on Implants and Their Effect on the Surrounding Bone: A Finite Element Analysis. Prosthesis 2024, 6, 74–88. [Google Scholar] [CrossRef]
- Wachol, K.; Morawiec, T.; Nowak-Wachol, A.; Kubaszek, B.; Kasprzyk-Kucewicz, T.; Baldi, D.; Machorowska-Pieniążek, A.; Skucha-Nowak, M.; Cholewka, A. Comparative Analysis of Implant Prosthesis Treatment Planning and Execution Following Bone Repair Procedures Using Dynamic Surgical Navigation in Augmented Areas. Coatings 2022, 12, 1099. [Google Scholar] [CrossRef]
- Shetty, M.; Prasad, D.K.; Mehra, D.R. Anatomical Considerations in Implant Selection and Positioning. Int. J. Oral Implantol. Clin. Res. 2013, 4, 24–29. [Google Scholar] [CrossRef]
- Fiorillo, L.; Milone, D.; D’Andrea, D.; Santonocito, D.; Risitano, G.; Cervino, G.; Cicciù, M. Finite Element Analysis of Zirconia Dental Implant. Prosthesis 2022, 4, 490–499. [Google Scholar] [CrossRef]
- do Vale Souza, J.P.; de Moraes Melo Neto, C.L.; Piacenza, L.T.; Freitas da Silva, E.V.; de Melo Moreno, A.L.; Penitente, P.A.; Brunetto, J.L.; Dos Santos, D.M.; Goiato, M.C. Relation Between Insertion Torque and Implant Stability Quotient: A Clinical Study. Eur. J. Dent. 2021, 15, 618–623. [Google Scholar] [CrossRef]
- Dorogoy, A.; Rittel, D.; Shemtov-Yona, K.; Korabi, R. Modeling dental implant insertion. J. Mech. Behav. Biomed. Mater. 2017, 68, 42–50. [Google Scholar] [CrossRef]
- Lo Giudice, R.; Machado, P.S.; Dal Piva, A.M.; Tribst, J.P. Influence of Placement of Ultrashort Implant at Sub-Crestal, Crestal and Supra-Crestal Level with Titanium or Polyetheretherketone Hybrid Abutment: 3D Finite Element Analysis. Prosthesis 2023, 5, 721–732. [Google Scholar] [CrossRef]
- Wolff, J. The Law of Bone Remodelling; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Reginald, J.; Kalayarasan, M.; Chethan, K.N.; Dhanabal, P. Static, dynamic, and fatigue life investigation of a hip prosthesis for walking gait using finite element analysis. Int. J. Model. Simul. 2023, 43, 797–811. [Google Scholar] [CrossRef]
- Göktaş, H.; Subaşi, E.; Uzkut, M.; Kara, M.; Biçici, H.; Shirazi, H.; Chethan, K.N.; Mihçin, Ş. Optimization of Hip Implant Designs Based on Its Mechanical Behaviour. In Biomechanics in Medicine, Sport and Biology; Springer: Berlin/Heidelberg, Germany, 2022; pp. 37–43. [Google Scholar]
- Eram, A.; Zuber, M.; Keni, L.G.; Kalburgi, S.; Naik, R.; Bhandary, S.; Amin, S.; Badruddin, I.A. Finite element analysis of immature teeth filled with MTA, Biodentine and Bioaggregate. Comput. Methods Programs Biomed. 2020, 190, 105356. [Google Scholar] [CrossRef]
- Shaikh, N.; Shenoy, B.S.; Bhat, N.S.; Shetty, S.; Chetan, K.C. Wear estimation at the contact surfaces of oval shaped hip implants using finite element analysis. Cogent Eng. 2023, 10, 2222985. [Google Scholar] [CrossRef]
- Gutmann, C.; Shaikh, N.; Shenoy, B.S.; Bhat, N.S.; Keni, L.G.; Chetan, K.C. Wear estimation of hip implants with varying chamfer geometry at the trunnion junction: A finite element analysis. Biomed. Phys. Eng. Express 2023, 9, 035004. [Google Scholar] [CrossRef] [PubMed]
- Blume, O.; Wildenhof, J.; Otto, S.; Probst, F. Influence of Clinical Parameters on the Primary Stability of a Tapered Dental Implant: A Retrospective Analysis. Int. J. Oral Maxillofac. Implants 2021, 36, 762–770. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, M.G.A.; Fonseca, E.M.M.; Natal, R.J. Thermal analysis during bone drilling using rigid polyurethane foams: Numerical and experimental methodologies. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 1855–1863. [Google Scholar] [CrossRef]
- Prasannavenkadesan, V.; Pandithevan, P. An in-silico bone drilling protocol to control thrust forces using finite element analysis coupled with the constitutive models. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 236, 8201–8210. [Google Scholar] [CrossRef]
- Khoddami, A.S.; Nasiri, M.A.; Mohammadi, B. Experimental and numerical study on micro-blasting process of 3A dental implant titanium alloy: A comparison between finite element method and smoothed particle hydrodynamics. J. Mech. Behav. Biomed. Mater. 2022, 132, 105269. [Google Scholar] [CrossRef] [PubMed]
- Škrlec, A.; Klemenc, J. Estimating the Strain-Rate-Dependent Parameters of the Cowper-Symonds and Johnson-Cook Material Models using Taguchi Arrays. Strojniški Vestn. J. Mech. Eng. 2016, 62, 220–230. [Google Scholar] [CrossRef]
- Fernandes, M.G.; Fonseca, E.M.; Jorge, R.N. Thermo-mechanical stresses distribution on bone drilling: Numerical and experimental procedures. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2019, 233, 637–646. [Google Scholar] [CrossRef]
- ANSYS LS-DYNA User’s Guide. 2023. Available online: https://ftp.lstc.com/anonymous/outgoing/web/ls-dyna_manuals/DRAFT/DRAFT_Theory.pdf (accessed on 15 October 2023).
- Prasannavenkadesan, V.; Pandithevan, P. Johnson–Cook Model Combined with Cowper–Symonds Model for Bone Cutting Simulation with Experimental Validation. J. Mech. Med. Biol. 2021, 21, 2150010. [Google Scholar] [CrossRef]
- Li, Z.; Kindig, M.W.; Kerrigan, J.R.; Untaroiu, C.D.; Subit, D.; Crandall, J.R.; Kent, R.W. Rib fractures under anterior–posterior dynamic loads: Experimental and finite-element study. J. Biomech. 2010, 43, 228–234. [Google Scholar] [CrossRef]
- Mahendra, J.; Chand, Y.B.; Mahendra, L.; Fageeh, H.N.; Fageeh, H.I.; Ibraheem, W.; Alzahrani, K.M.; Alqahtani, N.M.; Alahmari, N.M.; Almagbol, M.; et al. Evaluation of Stress Distribution during Insertion of Tapered Dental Implants in Various Osteotomy Techniques: Three-Dimensional Finite Element Study. Materials 2021, 14, 7547. [Google Scholar] [CrossRef]
- Aslam, A.; Hassan, S.H.; Aslam, H.M.; Khan, D.A. Effect of platform switching on peri-implant bone: A 3D finite element analysis. J. Prosthet. Dent. 2019, 121, 935–940. [Google Scholar] [CrossRef]
- Niroomand, M.R.; Arabbeiki, M. Implant stability in different implantation stages: Analysis of various interface conditions. Informatics Med. Unlocked 2020, 19, 100317. [Google Scholar] [CrossRef]
- Di Stefano, D.A.; Perrotti, V.; Greco, G.B.; Cappucci, C.; Arosio, P.; Piattelli, A.; Iezzi, G. The effect of undersizing and tapping on bone to implant contact and implant primary stability: A histomorphometric study on bovine ribs. J. Adv. Prosthodont. 2018, 10, 227. [Google Scholar] [CrossRef] [PubMed]
- Demirbas, A.E.; Ekici, R.; Karakaya, M.; Alkan, A. Bone stress and damage distributions during dental implant insertion: A novel dynamic FEM analysis. Comput. Methods Biomech. Biomed. Eng. 2022, 25, 1381–1392. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Jansen, J.A.; Walboomers, X.F.; van den Beucken, J.J. Mechanical aspects of dental implants and osseointegration: A narrative review. J. Mech. Behav. Biomed. Mater. 2020, 103, 103574. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Liu, Y.; Yuan, X.; Ren, M.; Chen, X.; Luo, L.; Zheng, L.; Liu, Y. Three-dimensional finite element analysis of stress distribution on short implants with different bone conditions and osseointegration rates. BMC Oral Health 2023, 23, 220. [Google Scholar] [CrossRef]

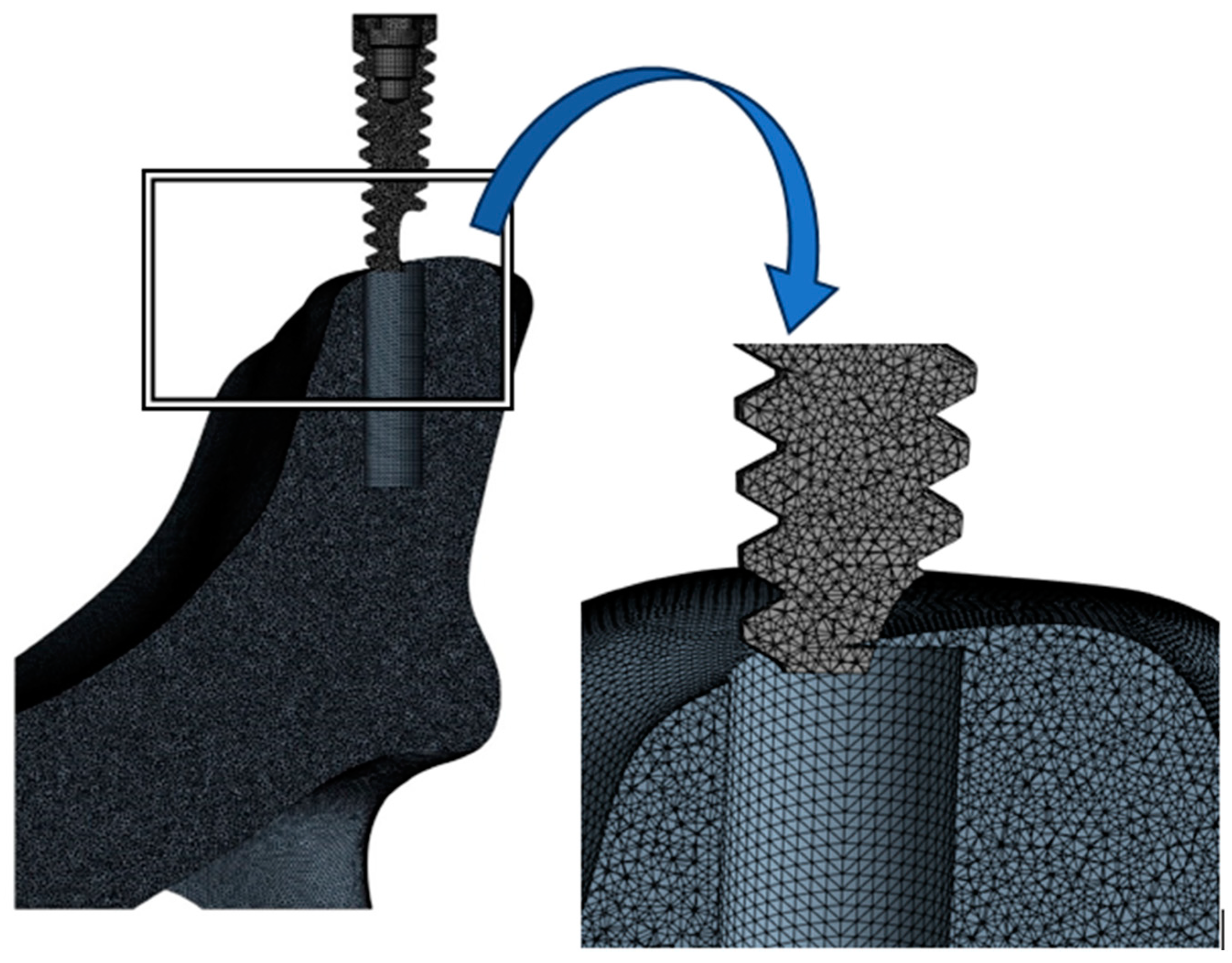
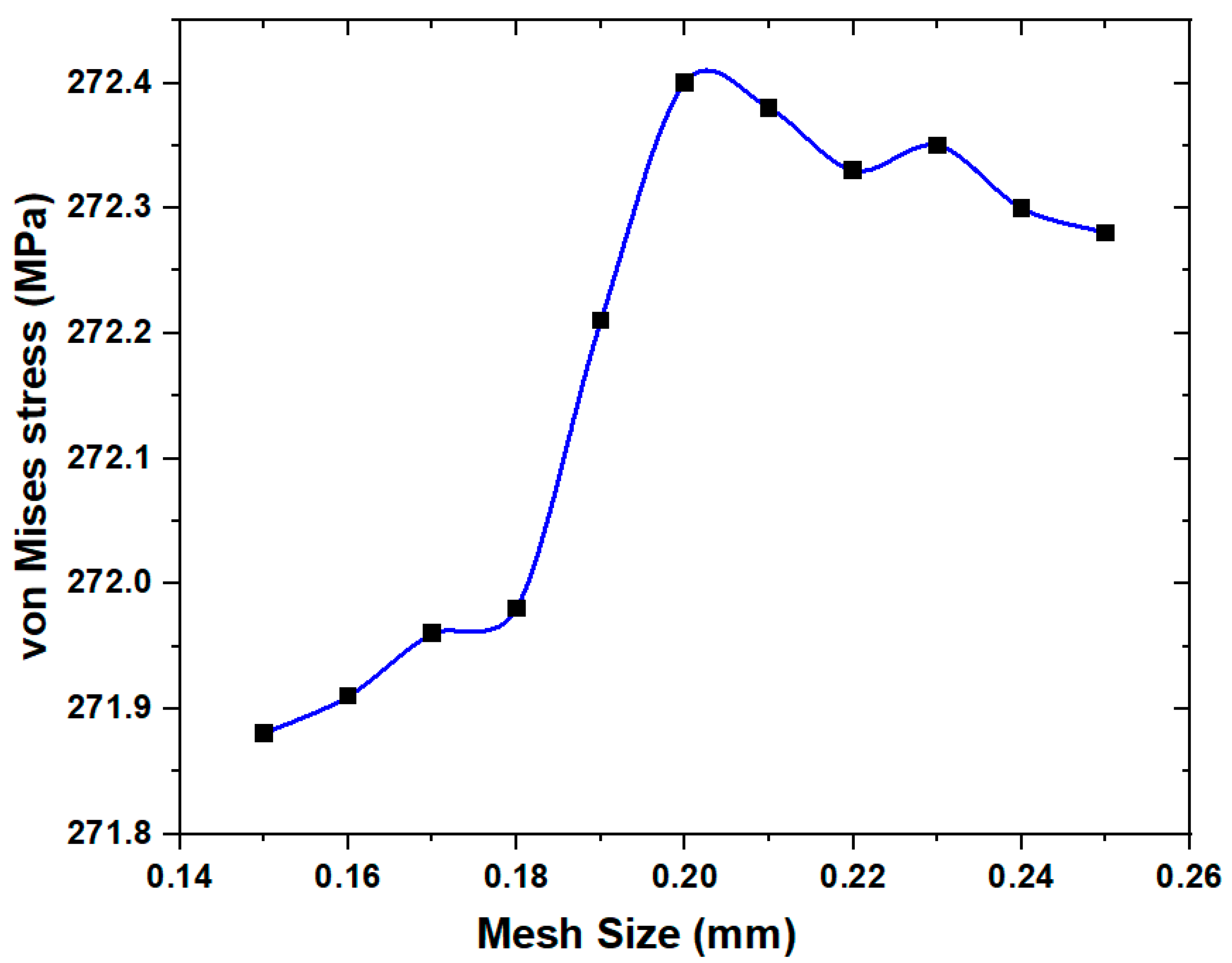
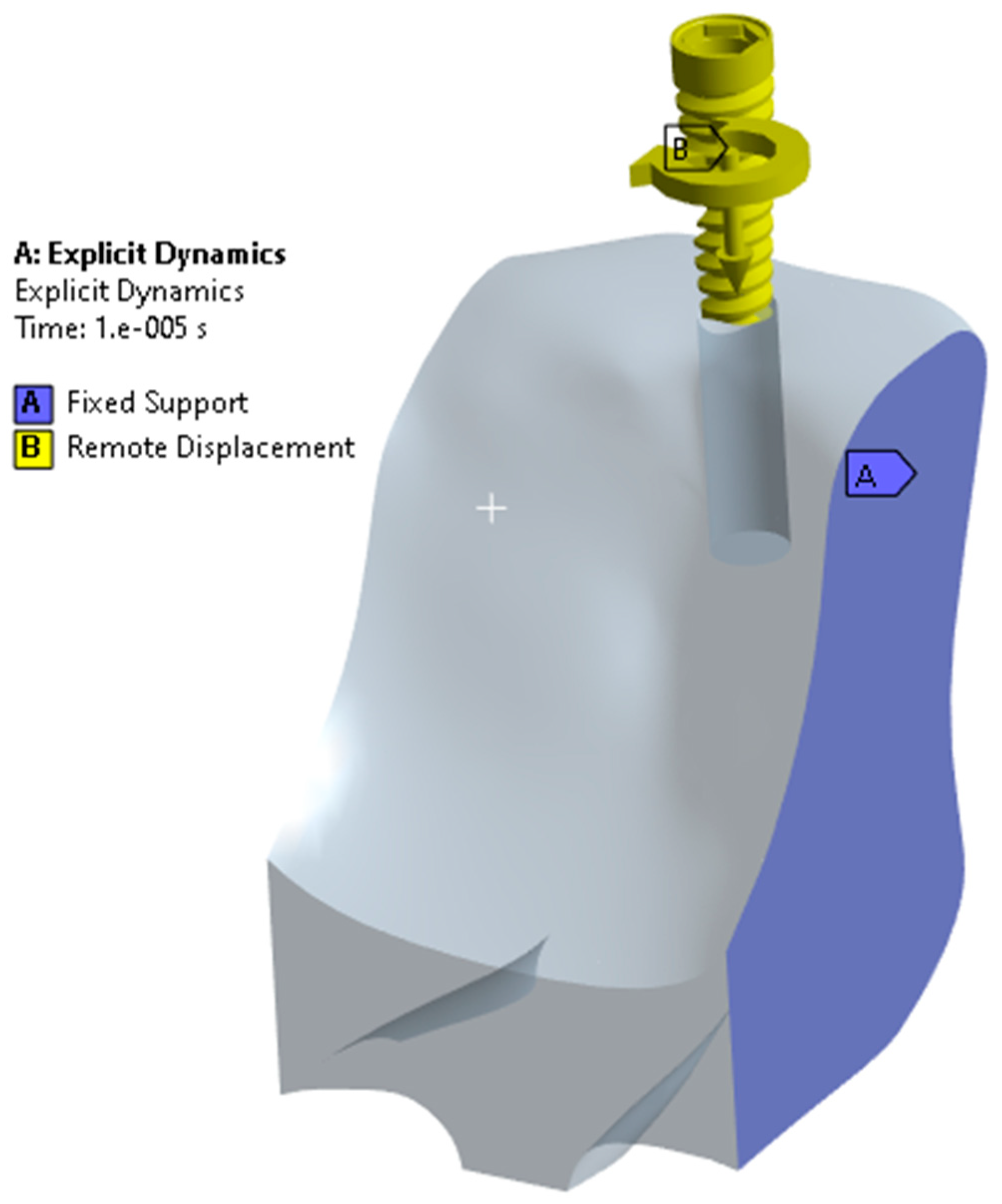

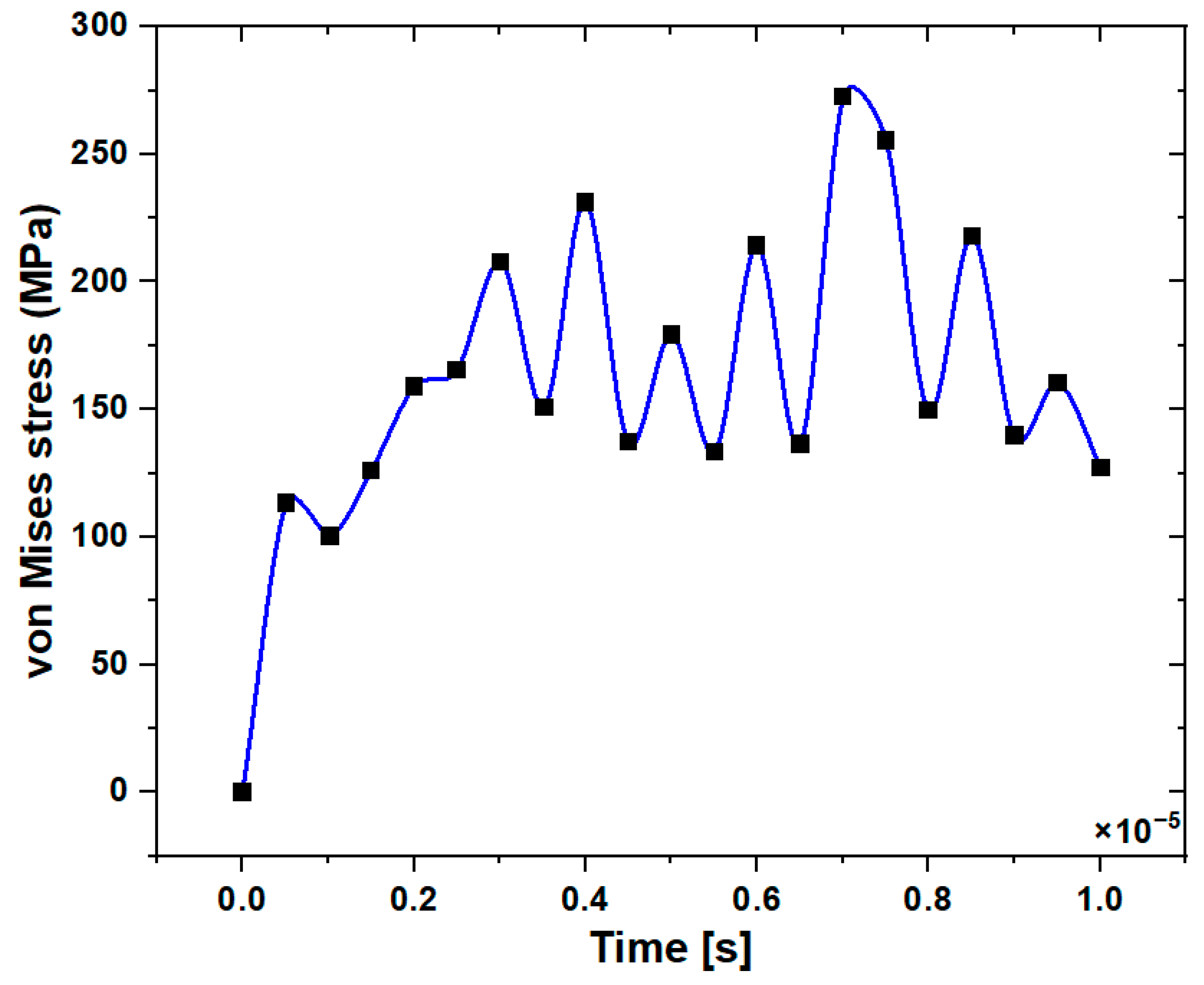

| Components | Node | Elements |
|---|---|---|
| Cancellous bone | 1,216,888 | 7,010,160 |
| Implant | 15,322 | 72,020 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
K N, C.; Eram, A.; Shetty, N.; Shetty, D.D.; Futane, M.; Keni, L.G. Exploring Stresses in Mandibular Jawbone during Implant Insertion: A Three-Dimensional Explicit Dynamic Analysis. Prosthesis 2024, 6, 301-314. https://doi.org/10.3390/prosthesis6020023
K N C, Eram A, Shetty N, Shetty DD, Futane M, Keni LG. Exploring Stresses in Mandibular Jawbone during Implant Insertion: A Three-Dimensional Explicit Dynamic Analysis. Prosthesis. 2024; 6(2):301-314. https://doi.org/10.3390/prosthesis6020023
Chicago/Turabian StyleK N, Chethan, Afiya Eram, Nisha Shetty, Divya D. Shetty, Mohan Futane, and Laxmikant G. Keni. 2024. "Exploring Stresses in Mandibular Jawbone during Implant Insertion: A Three-Dimensional Explicit Dynamic Analysis" Prosthesis 6, no. 2: 301-314. https://doi.org/10.3390/prosthesis6020023






