Evaluating Stresses in SiO2 Thin Films Using Molecular Dynamics Simulations †
Abstract
:1. Synthesis of SiO2 for Pre-Defined Application
2. Material System and PECVD Recipe
- i.
- Temperature control with a maximum rating up to 350 °C for PECVD is intended to allow for uniform deposition at low temperatures.
- ii.
- Vacuum systems with capability of chamber vacuum of 5000 mT.
- iii.
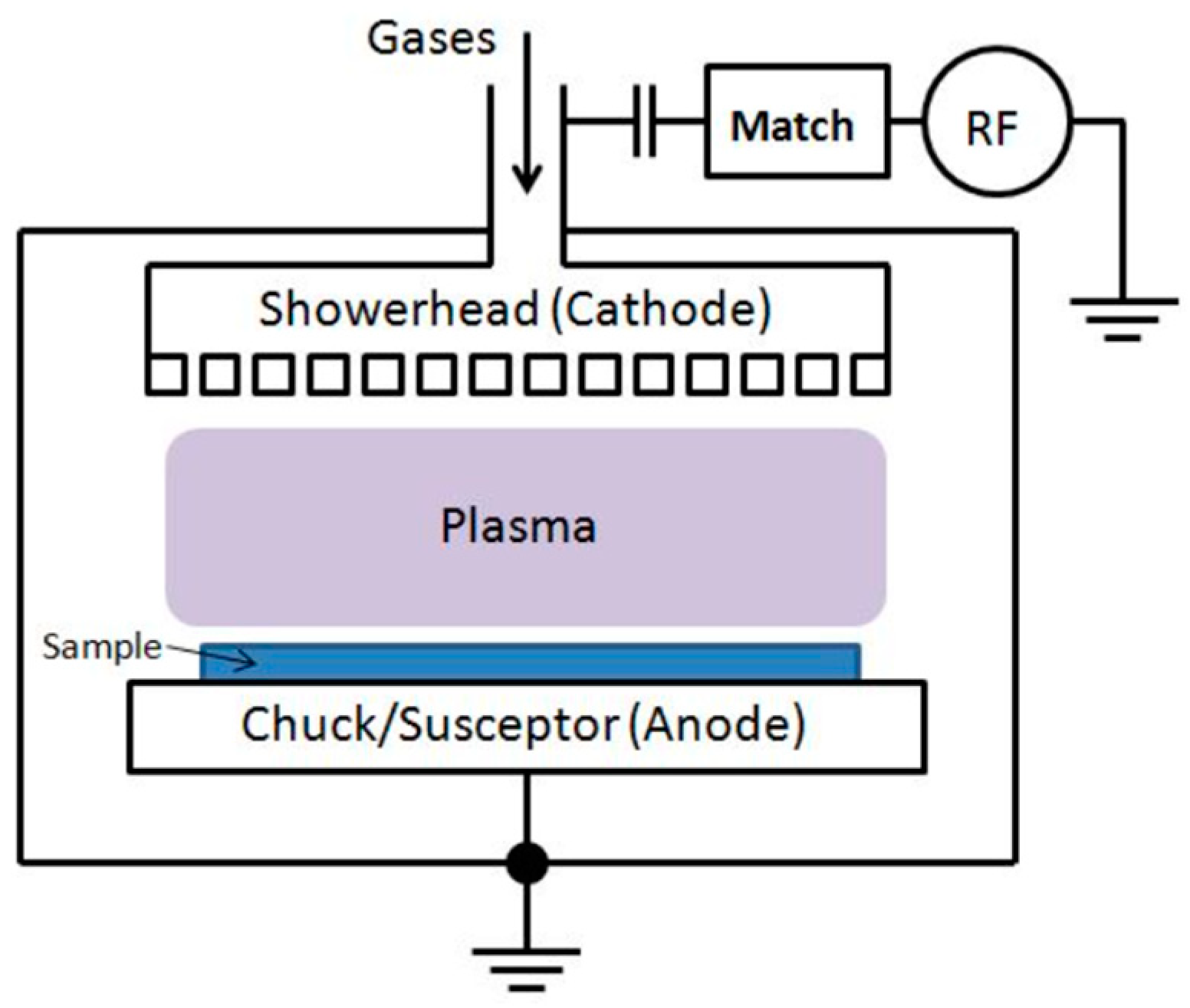
- A shower head chamber with Mass flow controllers (MFC) for Silane (usually SiH4) and MFC for N2O (1K, 5K), N2 (1K, 5K), Ar (1K, 5K), NH3, and SF6. Here, 1K and 5K are the mass flow capacities in square cubic centimeters (sccm). The SF6 MFC is useful for intermittent chamber cleaning.
- iv.
- High-frequency RF (13.56 MHz).
- v.
- Low-frequency RF.
3. Functional Properties
4. Experimental Stress Determination
- First, a production-quality Silicon Wafer lot was weighed on a weighing scale before deposition. Typically, the weight for each 150 mm diameter flat wafer was 25 to 28 gms, measured up to the fifth decimal, e.g., 25.97812 or 28.43109.
- The surface area for a standard 150 mm single notch wafer was computed.
- Once the virgin wafers were weighed, their initial stress without deposition of SiO2 was determined using the KLA Stress measuring machine. This initial stress state was used as reference surface stress after deposition.
- The deposition of SiO2 on a Si substrate by changing the PECVD input parameters was carried out. The input parameters of SiH4, N2O, RF Power, and SiO2 deposition were applied for 120 to 240 s.
- The thickness of SiO2 deposited was measured using a KLA Tencor spectroscopic ellipsometer. For example, some sample thicknesses of SiO2 deposition were about 1500 Å, equal to 0.15 µm or 0.000015 cm.
- Based on the above, data density was computed in kg/cm3, which should have been nearly equal to the standard value for SiO2 of 2.65 kg/cm3.
- The densities of the above values are shown below.
| Wafer Dia | Area (mm2) | Thk (Ang) | Thk (cm) | Area(cm2) | Vol (cm3) | wt (kg) | Density |
| 150 | 70,672.5 | 1500 | 0.000015 | 706.725 | 0.010601 | 0.028 | 2.641291 |
- 8.
- Final stress after deposition was measured to determine the thickness of deposition using a KLA laser scanner. Here, the laser scans the SiO2 surface for curvatures to assess thickness as per Stoney’s equation given above. The negative sign of stress in Table 2 corresponds to a convex curvature of SiO2 that causes compressive stresses. Ideally, the SiO2 deposition should have a value of −350 MPa to −50 MPa.
- 9.
- The refractive index was also computed along with thickness using a KLA Tencor SE instrument.
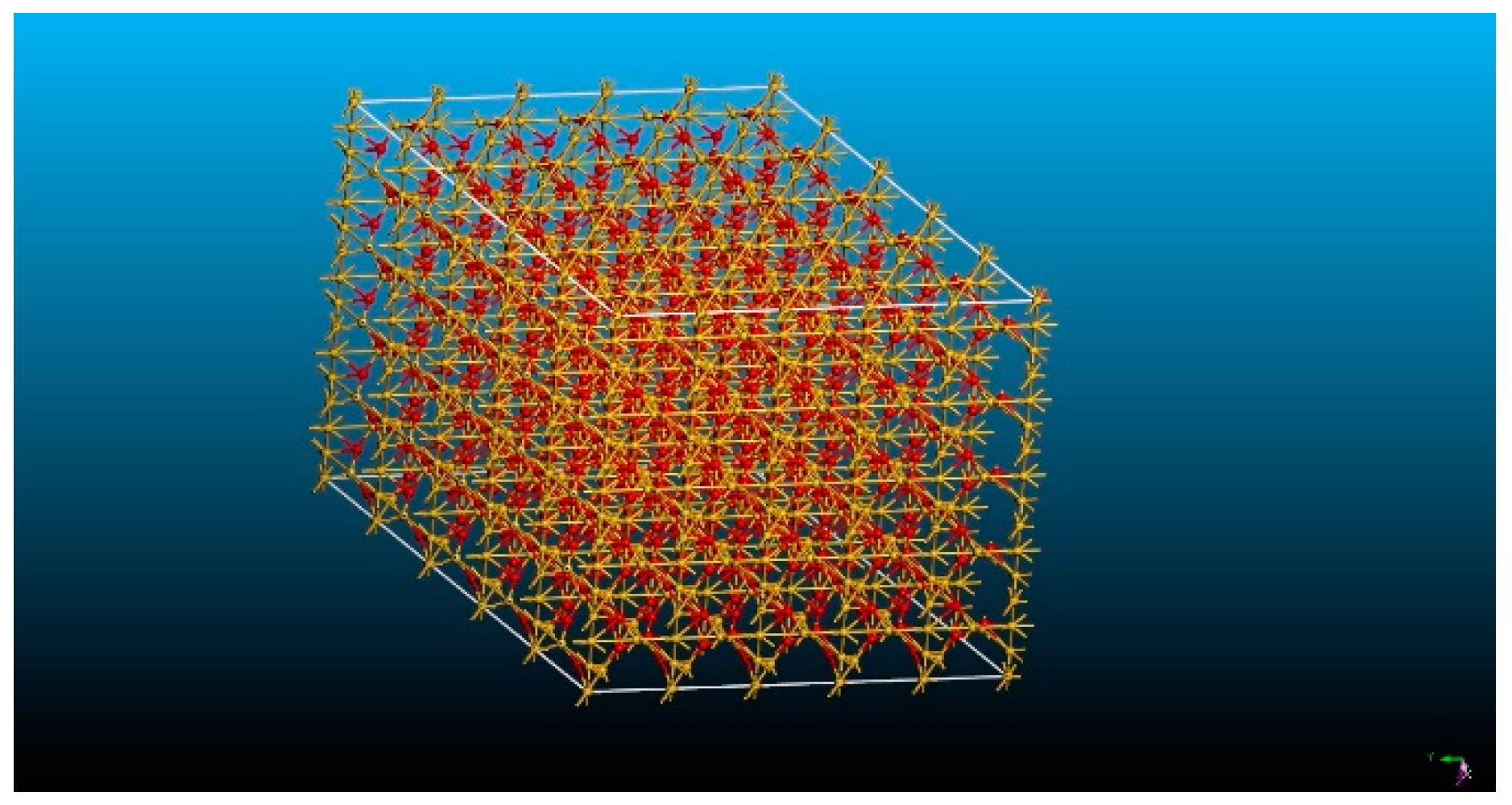
5. Computational Setup
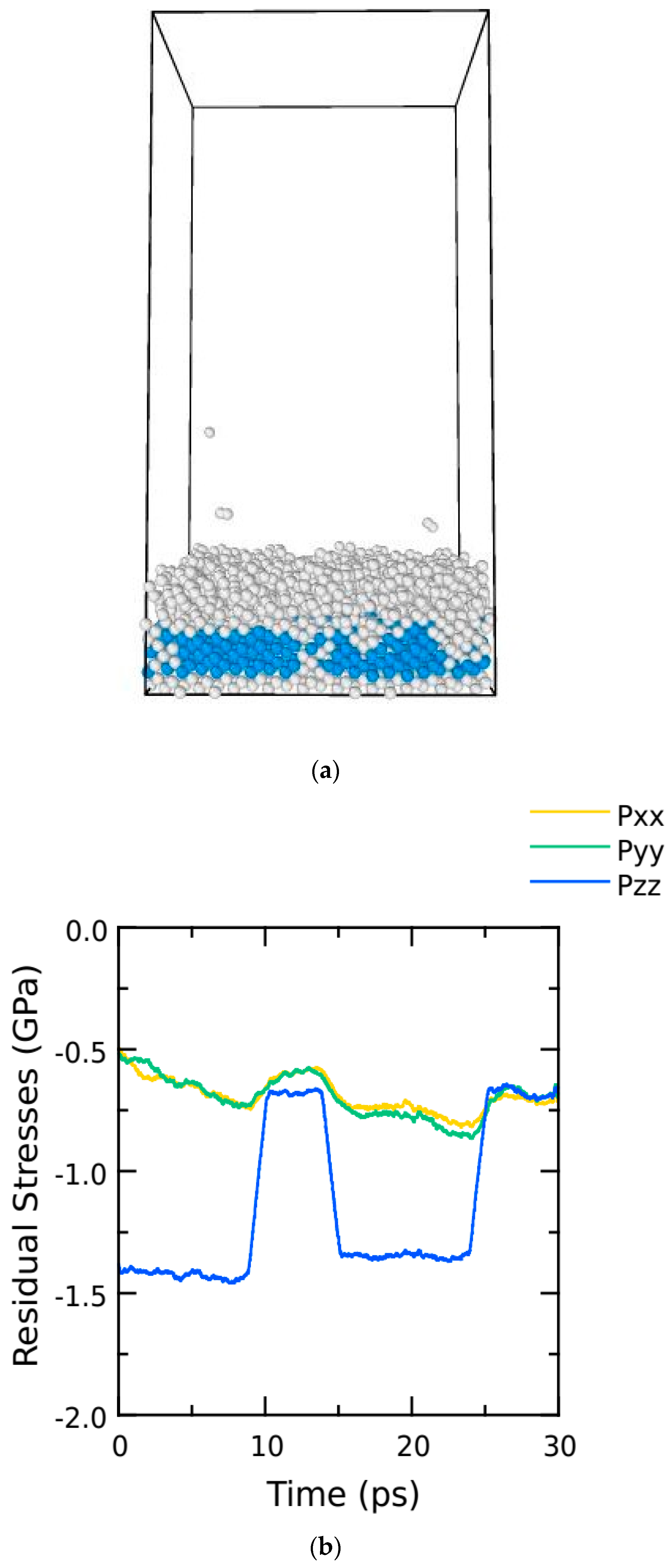
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ping, S.; Jie, L.; Gao, S.; Li, P.; Wang, X.; Wu, S.; Ma, Z. PECVD grown SiO2 film process optimization. In Silicon Photonics VI; SPIE: Bellingham, WA, USA, 2011; Volume 7943, pp. 352–357. [Google Scholar]
- Mackenzie, K.D.; Johnson, D.J.; DeVre, M.W.; Westerman, R.J.; Reelfs, B.H. Stress control of Si-based PECVD dielectrics. In Proceedings of the 207th Electrochemical Society Meeting, Quebec, QC, Canada, 15–20 May 2005; pp. 148–159. [Google Scholar]
- BIOVIA Materials Studio. Available online: https://www.3ds.com/products/biovia/materials-studio (accessed on 12 October 2023).
- SiO₂ mp-6930. Available online: https://next-gen.materialsproject.org/materials/mp-6930#properties (accessed on 12 October 2023).
- Kulkarni, A.D.; Truhlar, D.G.; Goverapet Srinivasan, S.; van Duin AC, T.; Norman, P.; Schwartzentruber, T.E. Oxygen interactions with silica surfaces: Coupled cluster and density functional investigation and the development of a new ReaxFF potential. J. Phys. Chem. C 2013, 117, 258–269. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based matrials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 10817. [Google Scholar] [CrossRef]
- Available online: https://en.wikipedia.org/wiki/Silicon_dioxide (accessed on 12 October 2023).
- Grigoriev, F.V.; Sulimov, A.V.; Katkova, E.V.; Kochikov, I.V.; Kondakova, O.A.; Sulimov, V.B.; Tikhonravov, A.V. Computational Experiments on Atomistic Modeling of Thin Film Deposition. Appl. Opt. 2017, 56, C87–C90. [Google Scholar] [CrossRef] [PubMed]
- Grigoriev, F.V.; Sulimov, V.B. Atomistic Simulation of Physical Vapor Deposition of Optical Thin Films. Nanomaterials 2023, 13, 1717. [Google Scholar] [CrossRef] [PubMed]


| Recipe Parameters |  | |
| Time | 02:00.0 | |
| Pressure | 1500 | |
| SiH4 1K | 500 | |
| SiH4 5K | -- | |
| NH3 50 | -- | |
| SF6 1K | -- | |
| AR 5K | 2000 | |
| N2O 5K | 2000 | |
| N2 5K | -- | |
| RF1 | 200 | |
| RF2 | -- |
| SiH4 | N2O | RF Power | Thickness | Density | RF Index | Stress |
|---|---|---|---|---|---|---|
| 150 | 770 | 300 | 1488 | 2.1878 | 1.4532 | −218.752 |
| 165 | 840 | 330 | 1806 | 2.1892 | 1.4583 | −279.463 |
| 135 | 700 | 270 | 1457 | 2.1973 | 1.4563 | −319.317 |
| Sr No. | Temperature (K) | Strain Rate (s−1) | Young’s Modulus (GPA) |
|---|---|---|---|
| 1 | 300 | 105 | 61.38 |
| 2 | 300 | 107 | 65.55 |
| 3 | 300 | 109 | 75.49 |
| 4 | 300 | 1011 | 78.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shendokar, S.; Ingle, N.; Mohan, R.; Aravamudhan, S. Evaluating Stresses in SiO2 Thin Films Using Molecular Dynamics Simulations. Eng. Proc. 2023, 56, 230. https://doi.org/10.3390/ASEC2023-16369
Shendokar S, Ingle N, Mohan R, Aravamudhan S. Evaluating Stresses in SiO2 Thin Films Using Molecular Dynamics Simulations. Engineering Proceedings. 2023; 56(1):230. https://doi.org/10.3390/ASEC2023-16369
Chicago/Turabian StyleShendokar, Sachin, Nikhil Ingle, Ram Mohan, and Shyam Aravamudhan. 2023. "Evaluating Stresses in SiO2 Thin Films Using Molecular Dynamics Simulations" Engineering Proceedings 56, no. 1: 230. https://doi.org/10.3390/ASEC2023-16369






