Quantifying Clinician-Controlled Preload in Dental Implants: Analysis of Manual Tightening Torque and Complication Rates †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Technical Implementation, Software, and Comprehensive Mathematical Framework
2.1.1. Hardware Configuration
2.1.2. Software Infrastructure
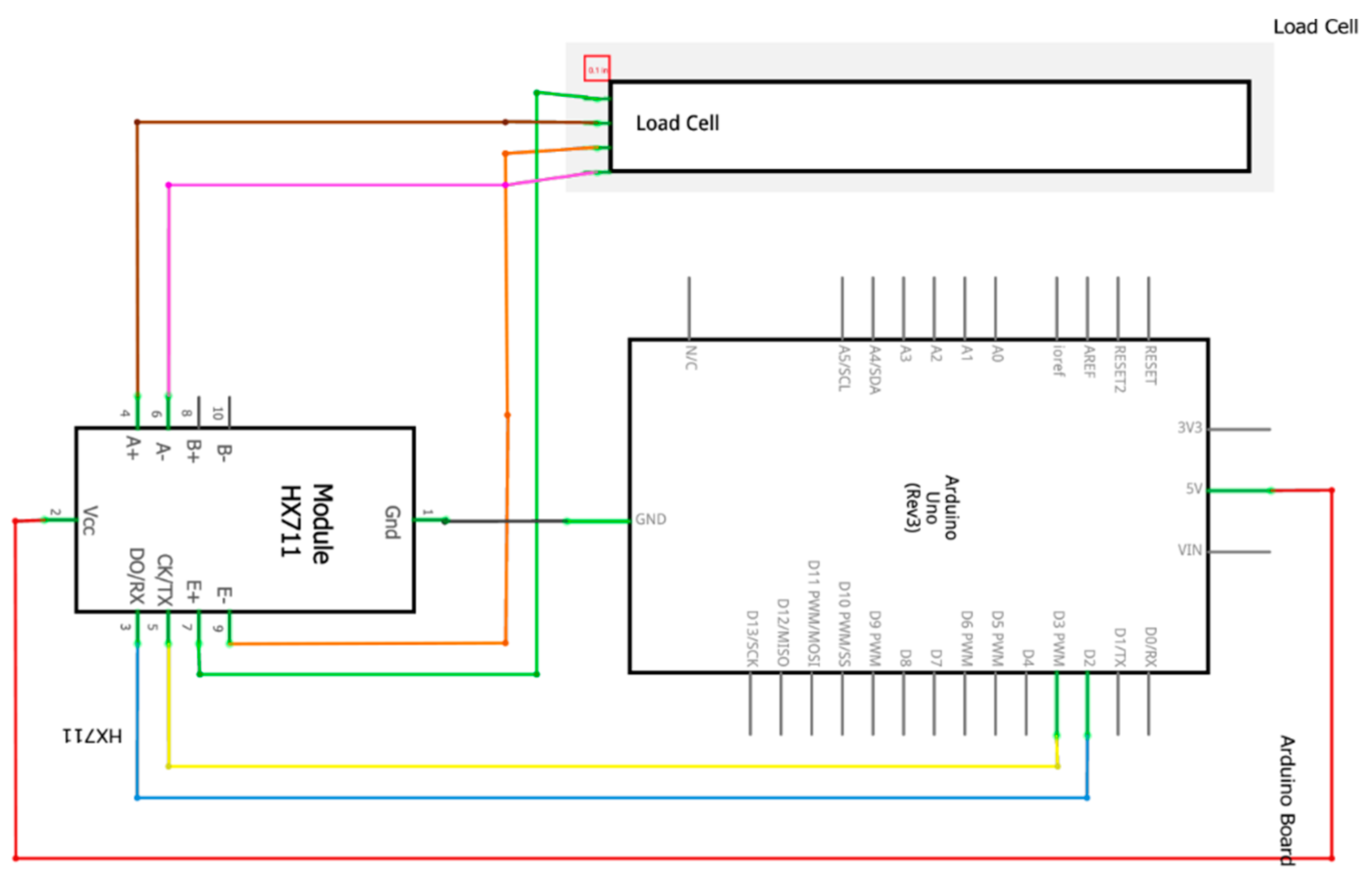
2.1.3. Wiring and Signal Pathways
- E+ (Green) of the load cell connects to E+ of the HX711 and also to the Arduino GND.
- E− (Orange) connects to E− of the HX711.
- A− (Brown) connects to A− of the HX711.
- A+ (Purple) connects to A+ of the HX711.
- HX711 VCC is connected to Arduino 5V.
2.1.4. Calibration
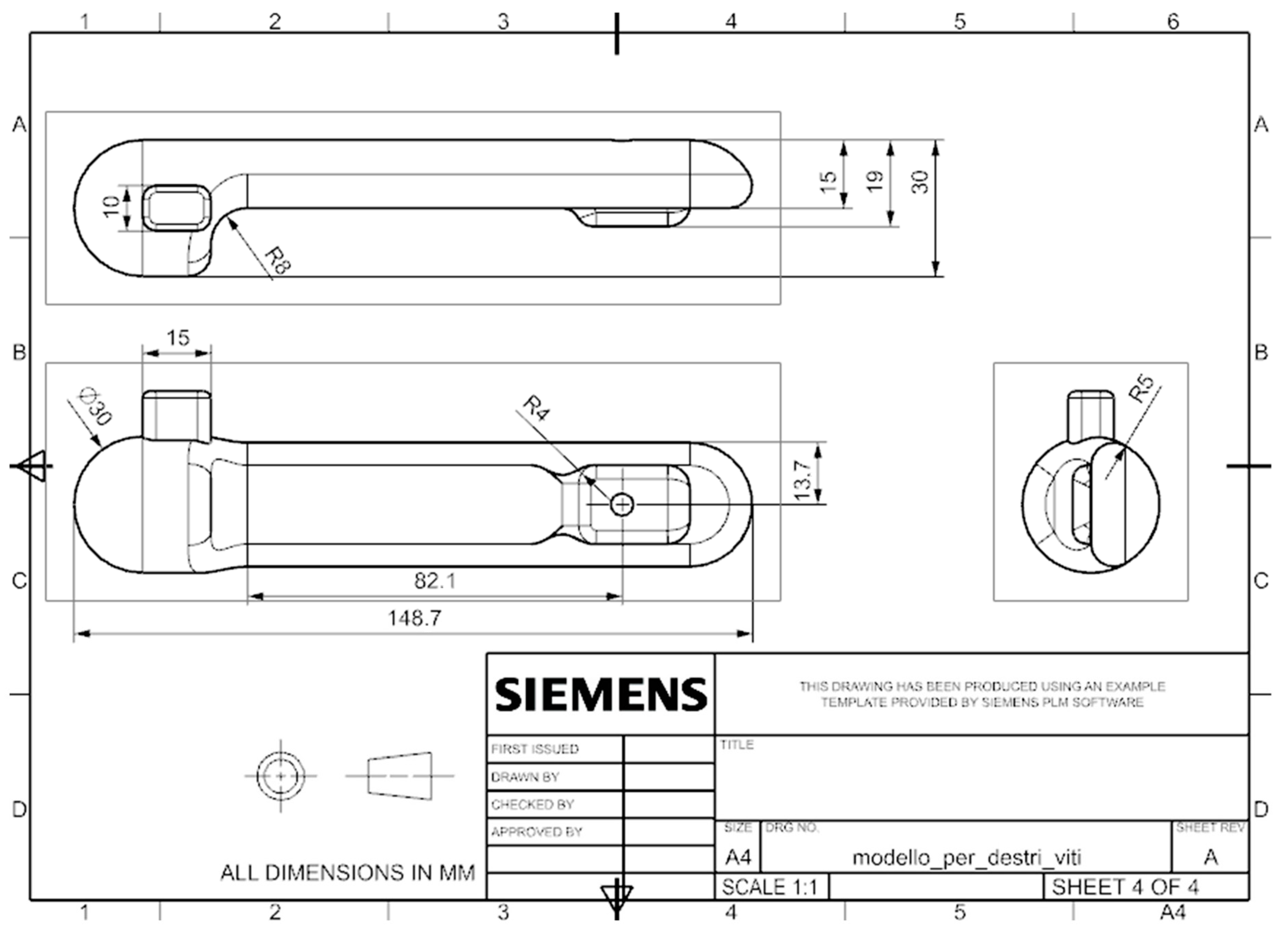
2.1.5. Design Prototype
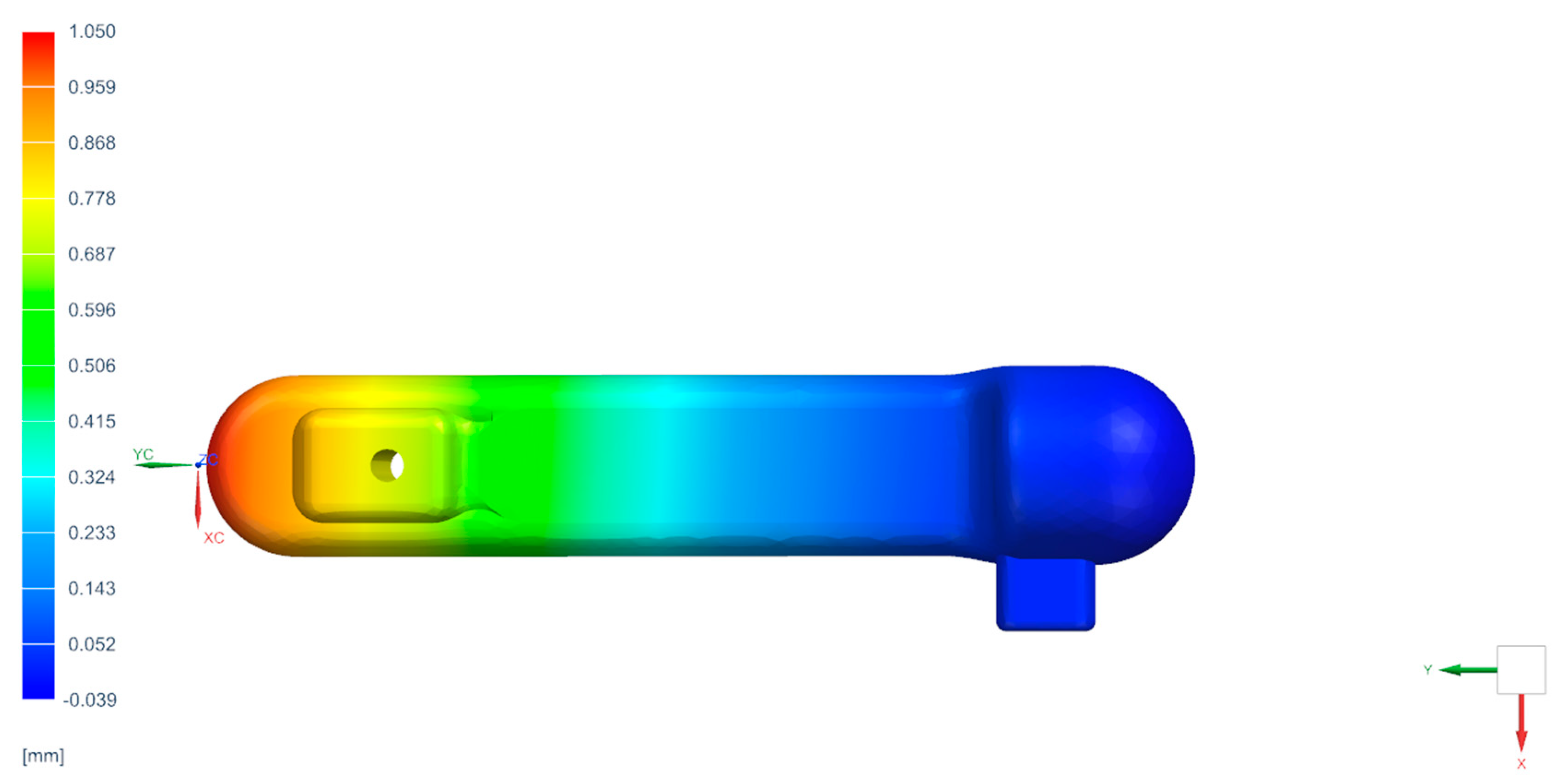
2.1.6. FEM Analysis
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wieser, M.; Liu, J.; Hernandez, P.; La Belle, J.T. A Comparison of Force Sensing for Applications in Prosthetic Haptic Feedback. Crit. Rev. Biomed. Eng. 2019, 47, 109–119. [Google Scholar] [CrossRef] [PubMed]
- Hendrich, N.; Wasserfall, F.; Zhang, J. 3D Printed Low-Cost Force-Torque Sensors. IEEE Access 2020, 8, 140569–140585. [Google Scholar] [CrossRef]
- Rasheedha, A.; Srinathi, K.; Sivalavanya, T.; Monesha, R.R.; Nithin, S. Arduino based Automated Dosage Prescriptor using Load Cell. In Proceedings of the 2020 4th International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 5–7 November 2020; pp. 85–89. [Google Scholar] [CrossRef]
- Hubbard, B.R.; Pearce, J.M. Open-Source Digitally Replicable Lab-Grade Scales. Instruments 2020, 4, 18. [Google Scholar] [CrossRef]
- Kondaveeti, H.K.; Kumaravelu, N.K.; Vanambathina, S.D.; Mathe, S.E.; Vappangi, S. A systematic literature review on prototyping with Arduino: Applications, challenges, advantages, and limitations. Comput. Sci. Rev. 2021, 40, 100364. [Google Scholar] [CrossRef]
- Fiorillo, L.; Milone, D.; D’Andrea, D.; Santonocito, D.; Risitano, G.; Cervino, G.; Cicciù, M. Finite Element Analysis of Zirconia Dental Implant. Prosthesis 2022, 4, 490–499. [Google Scholar] [CrossRef]
- Milone, D.; Fiorillo, L.; Alberti, F.; Cervino, G.; Filardi, V.; Pistone, A.; Cicciù, M.; Risitano, G. Stress distribution and failure analysis comparison between Zirconia and Titanium dental implants. Procedia Struct. Integr. 2022, 41, 680–691. [Google Scholar] [CrossRef]
- Milone, D.; Risitano, G.; Pistone, A.; Crisafulli, D.; Alberti, F. A New Approach for the Tribological and Mechanical Characterization of a Hip Prosthesis Trough a Numerical Model Based on Artificial Intelligence Algorithms and Humanoid Multibody Model. Lubricants 2022, 10, 160. [Google Scholar] [CrossRef]
- Milone, D.; Nicita, F.; Cervino, G.; Santonocito, D.; Risitano, G. Finite element analysis of OT bridge fixed prosthesis system. Procedia Struct. Integr. 2021, 33, 734–747. [Google Scholar] [CrossRef]
- Cervino, G.; Cicciù, M.; Fedi, S.; Milone, D.; Fiorillo, L. FEM analysis applied to OT bridge abutment with seeger retention system. Eur. J. Dent. 2020, 15, 47–53. [Google Scholar] [CrossRef] [PubMed]
- Parnia, F.; Yazdani, J.; Fakour, P.; Mahboub, F.; Pakdel, S.M.V. Comparison of the maximum hand-generated torque by professors and postgraduate dental students for tightening the abutment screws of dental implants. J. Dent. Res. Dent. Clin. Dent. Prospect. 2018, 12, 190. [Google Scholar] [CrossRef] [PubMed]
- Kose, O.D.; Karataslı, B.; Demircan, S.; Kose, T.E.; Cene, E.; Aya, S.A.; Erdem, M.A.; Cankaya, A.B. In vitro evaluation of manual torque values applied to implant-abutment complex by different clinicians and abutment screw loosening. BioMed Res. Int. 2017, 2017, 7376261. [Google Scholar] [CrossRef]
- Kanawati, A.; Richards, M.W.; Becker, J.J.; Monaco, N.E. Measurement of clinicians’ ability to hand torque dental implant components. J. Oral Implantol. 2009, 35, 185–188. [Google Scholar] [CrossRef] [PubMed]
- Goswami, M.M.; Kumar, M.; Vats, A.; Bansal, B.A.S. Evaluation of dental implant insertion torque using a manual ratchet. Med. J. Armed Forces India 2015, 71, S327–S332. [Google Scholar] [CrossRef] [PubMed]
- Choi, H.; Hong, M.H. Finite Element Analysis of the Effect of Tightening Torque on the Connection Stability of a Two-Piece Zirconia Implant System. Adv. Mater. Sci. Eng. 2022, 2022, 1456475. [Google Scholar] [CrossRef]
- Alnasser, A.H.; Wadhwani, C.P.K.; Alsarraf, E.Y.; Kattadiyil, M.T.; Lozada, J. Effect of implant abutment screw materials and tightening protocols on reverse tightening values: An in vitro study. J. Prosthet. Dent. 2023. [Google Scholar] [CrossRef] [PubMed]
- Nourizadeh, A.; Shafiee, E.; Khorramdel, A.; Mousavi, S.A.; Rahbar, M. Comparison of reverse torque values of abutment screws with the application of oil-based and water-based antibacterial agents. J. Dent. Res. Dent. Clin. Dent. Prospect. 2022, 16, 238. [Google Scholar] [CrossRef] [PubMed]
- Aloyaydi, B.; Sivasankaran, S.; Mustafa, A. Investigation of infill-patterns on mechanical response of 3D printed poly-lactic-acid. Polym. Test. 2020, 87, 106557. [Google Scholar] [CrossRef]

| Printing Specifications | |
|---|---|
| Density | 1.24 g/cm3 |
| Young’s modulus | 3100 MPa |
| Tensile strength | 60 MPa |
| Elongation | 9% |
| Printing Specifications | |
|---|---|
| Layer Height | 0.4 mm |
| Infill Density | 100% |
| Wall Line Count | 5 |
| Printing Temperature | 200 °C |
| Build Plate Temperature | 60 °C |
| Print Speed | 60 mm/s |
| Printing Specifications | |
|---|---|
| Element type | Tetra 10-Solid 186 |
| Numbers of elements | 23,905 |
| Numbers of nodes | 38,841 |
| Weight | Mean | Standard Deviation | RMSE | Rel Error |
|---|---|---|---|---|
| 0.01 kg | 0.0128 kg | 0.0060 kg | 0.0028 kg | 28% |
| 0.02 kg | 0.0210 kg | 0.0026 kg | 0.0010 kg | 5% |
| 0.05 kg | 0.0486 kg | 0.0040 kg | 0.0014 kg | 2.8% |
| 0.1 kg | 0.0977 kg | 4.9237 × 10−4 kg | 0.0023 kg | 2.3% |
| 0.5 kg | 0.4999 kg | 6.6299 × 10−4 kg | 1.0000 × 10−4 kg | 0.2% |
| 0.6 kg | 0.6030 kg | 1.1703 × 10−16 kg | 0.0030 kg | 0.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Milone, D.; Spataro, M.; D’Agati, L.; Fiorillo, L.; Risitano, G. Quantifying Clinician-Controlled Preload in Dental Implants: Analysis of Manual Tightening Torque and Complication Rates. Eng. Proc. 2023, 56, 252. https://doi.org/10.3390/ASEC2023-15955
Milone D, Spataro M, D’Agati L, Fiorillo L, Risitano G. Quantifying Clinician-Controlled Preload in Dental Implants: Analysis of Manual Tightening Torque and Complication Rates. Engineering Proceedings. 2023; 56(1):252. https://doi.org/10.3390/ASEC2023-15955
Chicago/Turabian StyleMilone, Dario, Marta Spataro, Luca D’Agati, Luca Fiorillo, and Giacomo Risitano. 2023. "Quantifying Clinician-Controlled Preload in Dental Implants: Analysis of Manual Tightening Torque and Complication Rates" Engineering Proceedings 56, no. 1: 252. https://doi.org/10.3390/ASEC2023-15955







