Enhancing Indoor Position Estimation Accuracy: Integration of Accelerometer, Raw Distance Data, and Extended Kalman Filter in Comparison to Vicon Motion Capture Data †
Abstract
:1. Introduction
2. Position Estimation Algorithm
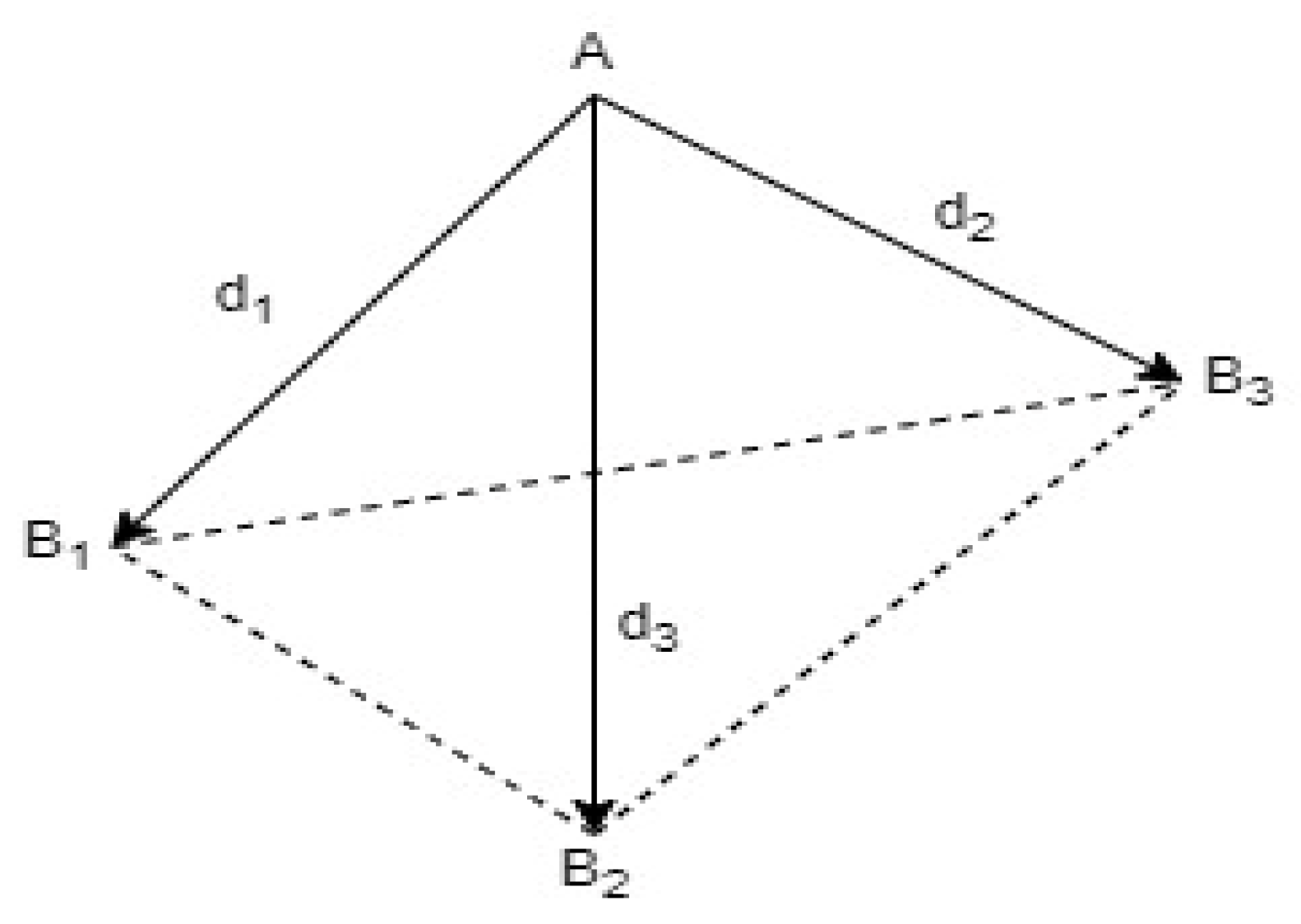
2.1. Geometric Approach
2.2. Sensor Fusion Algorithm
3. Implementation and Simulation System Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Valavanis, K.P.; Vachtsevanos, G.J. UAV Applications: Introduction; Springer: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Samad, T.; Bay, J.S.; Godbole, D. Network-centric systems for military operations in urban Terrain: The role of UAVs. Proc. IEEE 2007, 95, 92–107. [Google Scholar]
- Li, Z.; Liu, Y.; Walker, R.; Hayward, R.; Zhang, J. Towards automatic power line detection for a UAV surveillance system using pulse coupled neural filter and an improved Hough transform. Mach. Vis. Appl. 2010, 21, 677–686. [Google Scholar]
- Aiello, R.; Bar-Shalom, Y. Ultra-Wideband Technology for Precise Real-Time Location Systems. Proc. IEEE 2000, 88, 62–85. [Google Scholar]
- Heimovirta, E.; Salantera, S.; Röning, J. Real-Time Indoor Localization Using Ultra-Wideband Technology. In Proceedings of the 11th International Conference on Mobile and Ubiquitous Systems: Computing, Networking and Services, London, UK, 2–5 December 2014; pp. 265–274. [Google Scholar]
- Rhea, C.K. Accuracy and Precision of Vicon Motion Capture Systems for Tracking in 3D. Gait Posture 2004, 20, 332–335. [Google Scholar]
- Gentil, C.; de la Rouviere, S.; Elton, C. Vicon: A Computer Vision Solution for Reliable Real-Time 3D Motion Capture. J. NeuroEng. Rehabil. 2009, 6, 11. [Google Scholar]
- Benn, A.; Martin, A. Vicon Revue: Motion Capture Technology for Rehabilitation and Sports Medicine. Biomech. Med. Swim. 2004, IX, 122–126. [Google Scholar]
- Norrdine, A. An Algebraic Solution to the Multilateration Problem. In Proceedings of the 2012 International Conference on Indoor Positioning and Indoor Navigation, Sydney, Australia, 13–15 November 2012; pp. 1–4. [Google Scholar]
- Bodrumlu, T.; Caliskan, F. Indoor Position Estimation Using Ultrasonic Beacon Sensors and Extended Kalman Filter. Eng. Proc. 2022, 27, 16. [Google Scholar] [CrossRef]

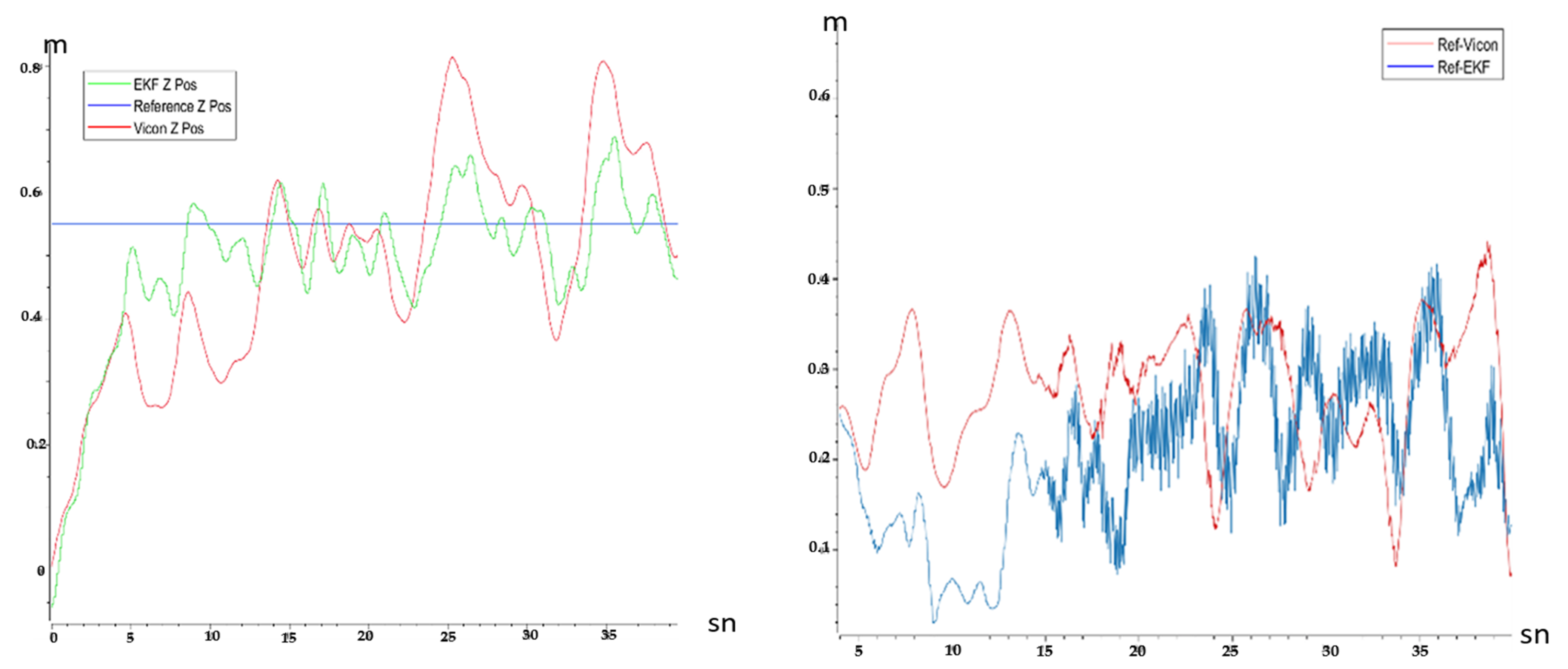
| Minimum Error (m) | Mean Error (m) | Maximum Error (m) | |
|---|---|---|---|
| Ref-EKF | 0.019 | 0.205 | 0.424 |
| Ref-Vicon | 0.07 | 0.255 | 0.441 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bodrumlu, T.; Çalışkan, F. Enhancing Indoor Position Estimation Accuracy: Integration of Accelerometer, Raw Distance Data, and Extended Kalman Filter in Comparison to Vicon Motion Capture Data. Eng. Proc. 2023, 58, 40. https://doi.org/10.3390/ecsa-10-16089
Bodrumlu T, Çalışkan F. Enhancing Indoor Position Estimation Accuracy: Integration of Accelerometer, Raw Distance Data, and Extended Kalman Filter in Comparison to Vicon Motion Capture Data. Engineering Proceedings. 2023; 58(1):40. https://doi.org/10.3390/ecsa-10-16089
Chicago/Turabian StyleBodrumlu, Tolga, and Fikret Çalışkan. 2023. "Enhancing Indoor Position Estimation Accuracy: Integration of Accelerometer, Raw Distance Data, and Extended Kalman Filter in Comparison to Vicon Motion Capture Data" Engineering Proceedings 58, no. 1: 40. https://doi.org/10.3390/ecsa-10-16089
APA StyleBodrumlu, T., & Çalışkan, F. (2023). Enhancing Indoor Position Estimation Accuracy: Integration of Accelerometer, Raw Distance Data, and Extended Kalman Filter in Comparison to Vicon Motion Capture Data. Engineering Proceedings, 58(1), 40. https://doi.org/10.3390/ecsa-10-16089






