A Hybrid MCDM-Grey Wolf Optimizer Approach for Multi-Objective Parametric Optimization of μ-EDM Process †
Abstract
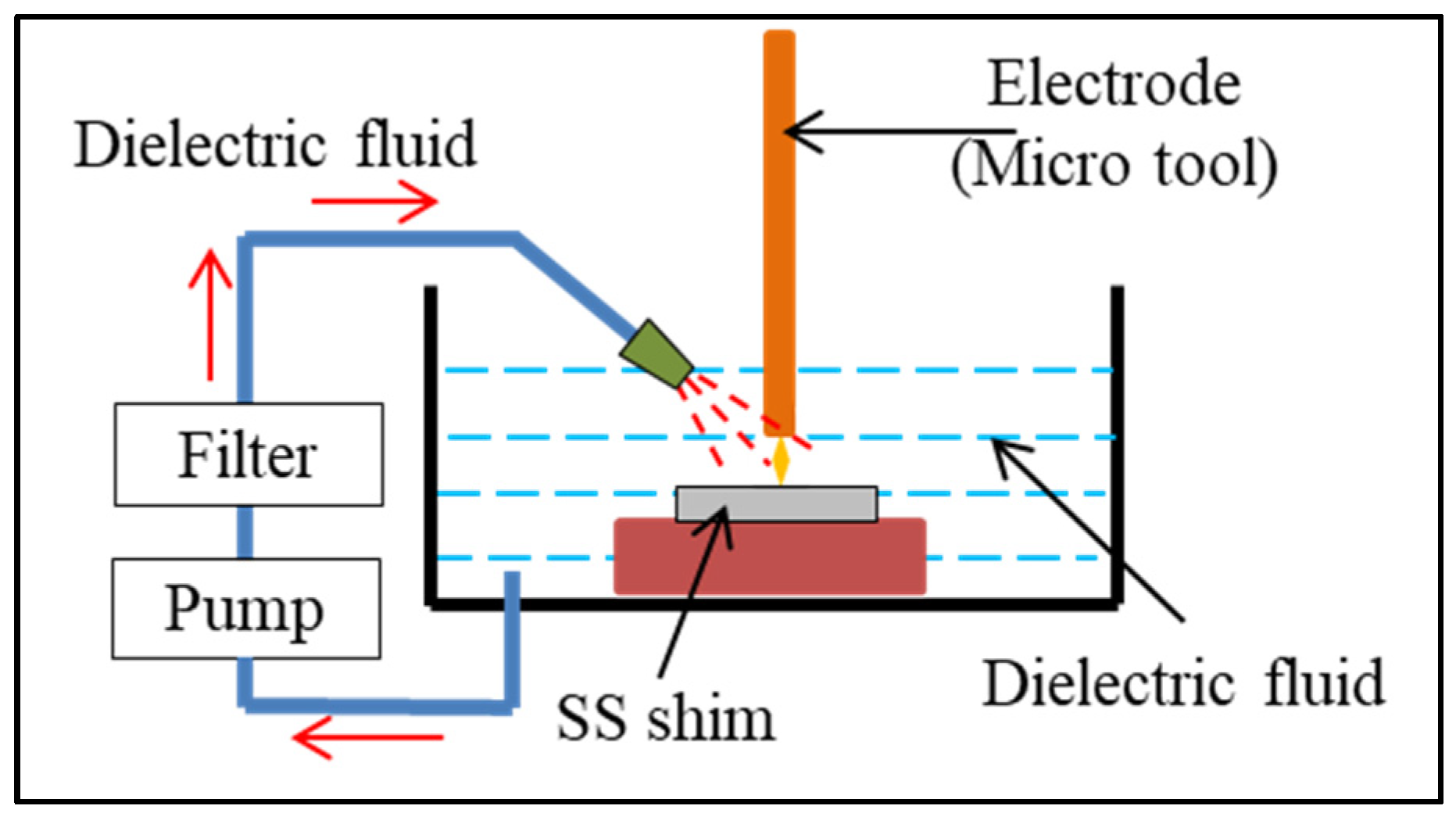
:1. Introduction
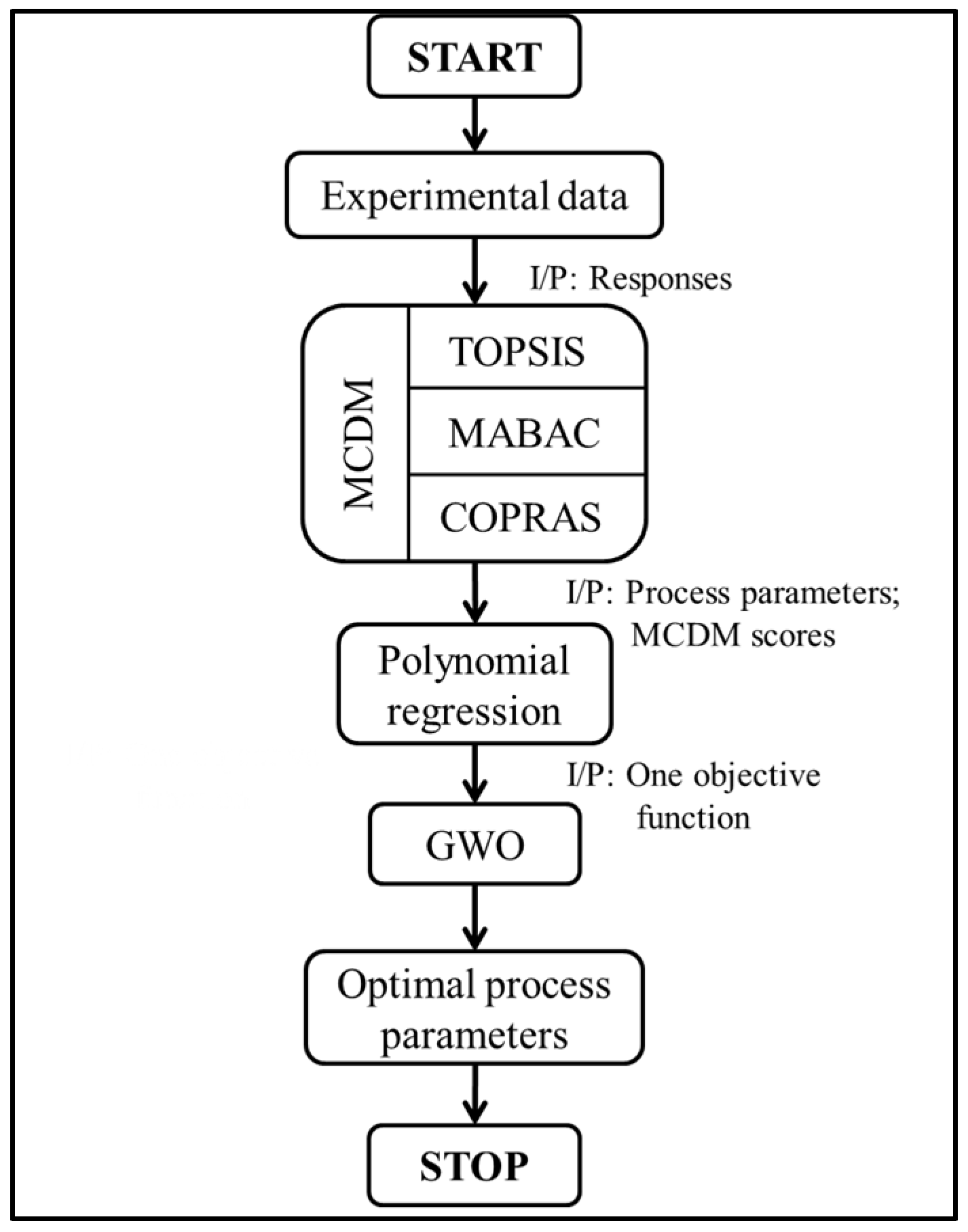
2. Methodology
2.1. PR Metamodel
2.2. Grey Wolf Optimizer
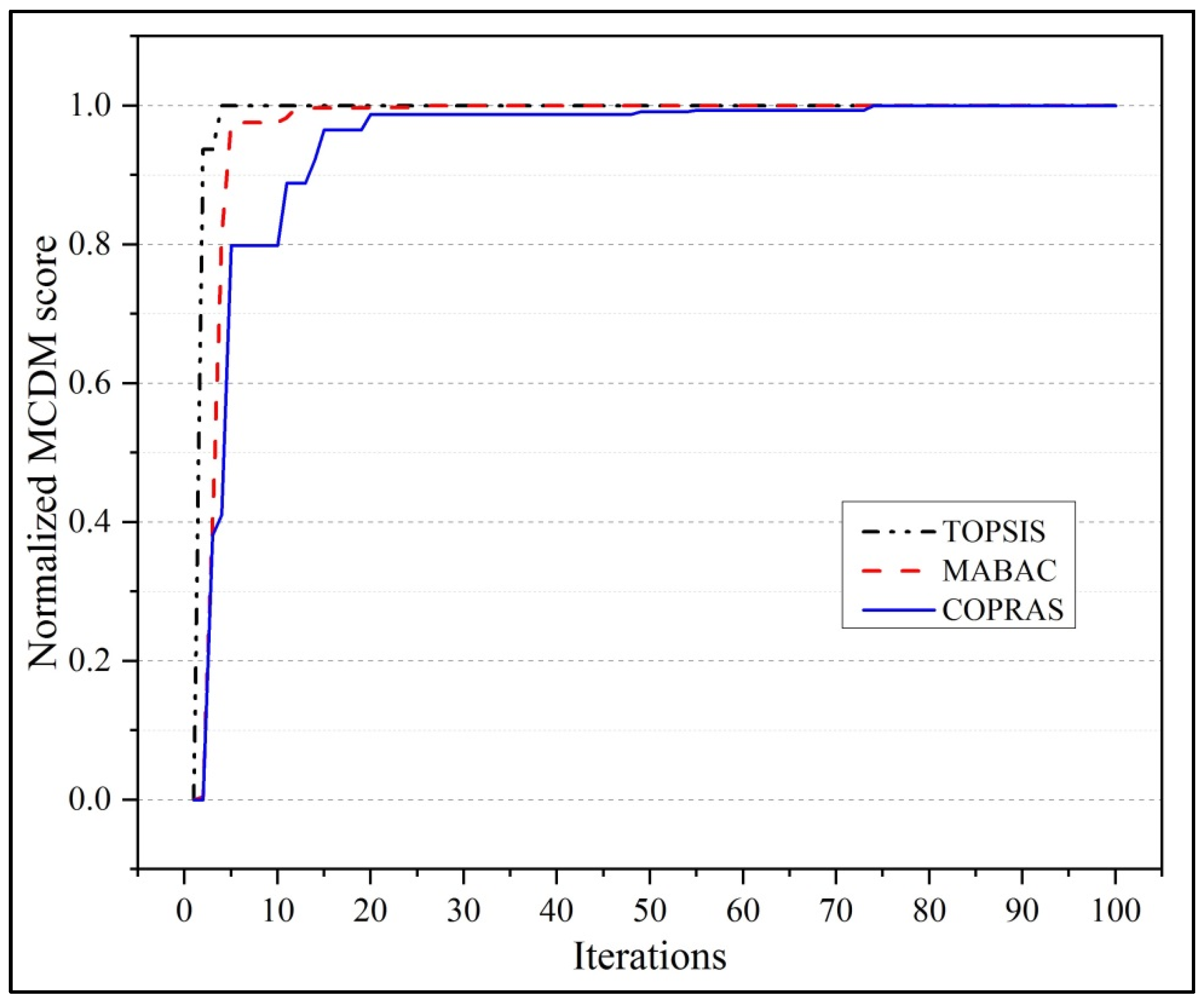
3. Results and Discussion
Parametric Optimization of μ-EDM Process
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumar, D.; Singh, N.K.; Bajpai, V. Recent trends, opportunities and other aspects of micro-EDM for advanced manufacturing: A comprehensive review. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 222. [Google Scholar] [CrossRef]
- Modica, F.; Marrocco, V.; Fassi, I. Micro-electro-discharge machining (micro-EDM). In Micro-Manufacturing Technologies and Their Applications: A Theoretical and Practical Guide; Fassi, I., Shipley, D., Eds.; Springer Tracts in Mechanical Engineering; Springer: Cham, Switzerland, 2017; pp. 149–173. [Google Scholar]
- Tiwary, A.P.; Pradhan, B.B.; Bhattacharyya, B. Study on the influence of micro-EDM process parameters during machining of Ti–6Al–4V superalloy. Int. J. Adv. Manuf. Technol. 2015, 76, 151–160. [Google Scholar] [CrossRef]
- Das, A.K.; Kumar, P.; Sethi, A.; Singh, P.K.; Hussain, M. Influence of process parameters on the surface integrity of micro-holes of SS304 obtained by micro-EDM. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 2029–2037. [Google Scholar] [CrossRef]
- Quarto, M.; D’Urso, G.; Giardini, C. Micro-EDM optimization through particle swarm algorithm and artificial neural network. Precis. Eng. 2022, 73, 63–70. [Google Scholar] [CrossRef]
- Nguyen, P.H.; Pham, D.V.; Shirguppikar, S.; Nguyen, T.N.; Nguyen, T.C.; Nguyen, L.T. Multi-objective optimization of micro EDM using TOPSIS method with Tungsten carbide electrode. Sādhanā 2022, 47, 133. [Google Scholar] [CrossRef]
- Das, P.P.; Tiwary, A.P.; Chakraborty, S. A hybrid MCDM approach for parametric optimization of a micro-EDM process. Int. J. Interact. Des. Manuf. 2022, 16, 1739–1759. [Google Scholar] [CrossRef]
- Pain, P.; Bose, G.K.; Bose, D. Parametric analysis and optimization of aluminium and SS 204 material using micro-EDM system. Int. J. Interact. Des. Manuf. 2023, 17, 3025–3042. [Google Scholar] [CrossRef]
- Sahu, J.; Mahapatra, S.S.; Mohanty, C.P. Multi–response optimisation of EDM parameters using data envelopment analysis. Int. J. Product. Qual. Manag. 2015, 15, 309–334. [Google Scholar] [CrossRef]
- Huu, P.N.; Muthuramalingam, T.; Van, D.P.; Shirguppikar, S.; Tien, D.H.; Van, T.N.; Trong, L.N. Multi-objects optimization in µ-edm using alcrni-coated tungsten carbide electrode for Ti-6Al-4V. Int. J. Adv. Manuf. Technol. 2022, 122, 2267–2276. [Google Scholar] [CrossRef]
- Santhanakumar, M.; Rajmohan, M. Application of desirability analysis for optimizing the micro wire electrical discharge machining (μWEDM) parameters. Appl. Mech. Mater. 2014, 592, 77–81. [Google Scholar] [CrossRef]
- Xu, J.; Xia, S.; Yu, P.; Li, M. Multi-objective parameter optimization of ultrasonic vibration–assisted micro-EDM of Ti-6Al-4V alloys. J. Vib. Control 2023. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, Y.; Cheng, M.; Zhu, J.; Meng, Y.; Mu, X. Performance prediction and parameter optimization of alumina-titanium carbide ceramic micro-EDM hole machining process based on XGBoost. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2023. [Google Scholar] [CrossRef]
- Kumar, K.; Singh, V.; Katyal, P.; Sharma, N. EDM μ-drilling in Ti-6Al-7Nb: Experimental investigation and optimization using NSGA-II. Int. J. Adv. Manuf. Technol. 2019, 104, 2727–2738. [Google Scholar] [CrossRef]
- Wang, G.G.; Shan, S. Review of metamodeling techniques in support of engineering design optimization. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Philadelphia, PA, USA, 10–13 September 2006; Volume 4255, pp. 415–426. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Faris, H.; Aljarah, I.; Al-Betar, M.A.; Mirjalili, S. Grey wolf optimizer: A review of recent variants and applications. Neural Comput. Appl. 2018, 30, 413–435. [Google Scholar] [CrossRef]
- Natarajan, U.; Suganthi, X.H.; Periyanan, P.R. Modeling and multiresponse optimization of quality characteristics for the micro-EDM drilling process. Trans. Indian Inst. Met. 2016, 69, 1675–1686. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Das, P.P.; Chakraborty, S. A comparative assessment of multicriteria parametric optimization methods for plasma arc cutting processes. Decis. Anal. J. 2023, 6, 100190. [Google Scholar] [CrossRef]
| Exp. no. | A (µm/s) | B (µm) | C (V) | MRR (mm3/min) | Ra (µm) | TWR |
|---|---|---|---|---|---|---|
| 1 | 2 | 0.1 | 80 | 0.003 | 0.36 | 1.64 |
| 2 | 4 | 0.1 | 80 | 0.008 | 0.38 | 0.54 |
| 3 | 6 | 0.1 | 80 | 0.01 | 0.38 | 1.78 |
| 4 | 2 | 0.1 | 100 | 0.004 | 0.41 | 2.38 |
| 5 | 4 | 0.1 | 100 | 0.008 | 0.45 | 1.32 |
| 6 | 6 | 0.1 | 100 | 0.008 | 0.52 | 2.32 |
| 7 | 2 | 0.1 | 120 | 0.007 | 0.42 | 2.68 |
| 8 | 4 | 0.1 | 120 | 0.017 | 0.45 | 0.89 |
| 9 | 6 | 0.1 | 120 | 0.012 | 0.54 | 1.92 |
| 10 | 2 | 1 | 80 | 0.004 | 1.1 | 2.23 |
| 11 | 4 | 1 | 80 | 0.01 | 1.2 | 1.32 |
| 12 | 6 | 1 | 80 | 0.01 | 1.2 | 2.35 |
| 13 | 2 | 1 | 100 | 0.007 | 1.9 | 2.68 |
| 14 | 4 | 1 | 100 | 0.018 | 1.82 | 1.28 |
| 15 | 6 | 1 | 100 | 0.016 | 1.88 | 2.62 |
| 16 | 2 | 1 | 120 | 0.008 | 1.9 | 2.88 |
| 17 | 4 | 1 | 120 | 0.038 | 1.82 | 1.19 |
| 18 | 6 | 1 | 120 | 0.018 | 1.82 | 2.23 |
| 19 | 2 | 10 | 80 | 0.007 | 3.8 | 2.46 |
| 20 | 4 | 10 | 80 | 0.011 | 3.7 | 1.23 |
| 21 | 6 | 10 | 80 | 0.013 | 3.7 | 2.78 |
| 22 | 2 | 10 | 100 | 0.01 | 4.2 | 2.92 |
| 23 | 4 | 10 | 100 | 0.036 | 4.8 | 1.82 |
| 24 | 6 | 10 | 100 | 0.012 | 4.4 | 2.82 |
| 25 | 2 | 10 | 120 | 0.022 | 5.2 | 3.16 |
| 26 | 4 | 10 | 120 | 0.046 | 5.9 | 1.58 |
| 27 | 6 | 10 | 120 | 0.014 | 4.8 | 3.12 |
| 28 | 4 | 1 | 100 | 0.009 | 1.88 | 1.2 |
| 29 | 4 | 1 | 100 | 0.052 | 1.86 | 1.48 |
| 30 | 4 | 1 | 100 | 0.024 | 1.65 | 1.38 |
| 31 | 4 | 1 | 100 | 0.014 | 1.74 | 1.36 |
| 32 | 4 | 1 | 100 | 0.022 | 1.7 | 1.54 |
| Condition | Output | A (µm/s) | B (µm) | C (V) | Optimal Value |
|---|---|---|---|---|---|
| Single-objective | MRR (mm3/min) | 3.9045 | 5.9608 | 120 | 0.047143 |
| Ra (µm) | 2 | 0.1 | 80 | 0.16287 | |
| TWR | 3.9195 | 0.1 | 80 | 0.63627 | |
| Multi-objective | MRR (mm3/min) | 3.55 | 0.158 | 80 | 0.0126 |
| Ra (µm) | 0.3892 | ||||
| TWR | 0.7042 |
| Exp No. | TOPSIS Score | MABAC Score | COPRAS Score |
|---|---|---|---|
| 1 | 0.4161 | −0.5082 | 0.0313 |
| 2 | 0.4913 | −0.3125 | 0.0751 |
| 3 | 0.449 | −0.4809 | 0.034 |
| 4 | 0.3887 | −0.6125 | 0.0235 |
| 5 | 0.455 | −0.4306 | 0.0395 |
| 6 | 0.407 | −0.5811 | 0.0261 |
| 7 | 0.392 | −0.6361 | 0.0234 |
| 8 | 0.5439 | −0.3045 | 0.058 |
| 9 | 0.4505 | −0.4953 | 0.0324 |
| 10 | 0.365 | −0.6243 | 0.0214 |
| 11 | 0.4421 | −0.4535 | 0.0329 |
| 12 | 0.3881 | −0.605 | 0.0244 |
| 13 | 0.3204 | −0.7089 | 0.0188 |
| 1 4 | 0.4884 | −0.4222 | 0.0346 |
| 15 | 0.3882 | −0.6361 | 0.0253 |
| 16 | 0.3185 | −0.7313 | 0.0188 |
| 17 | 0.7263 | −0.2691 | 0.0492 |
| 18 | 0.4304 | −0.5619 | 0.0284 |
| 19 | 0.2174 | −0.7699 | 0.0159 |
| 20 | 0.3546 | −0.5561 | 0.0226 |
| 21 | 0.2523 | −0.7701 | 0.0195 |
| 22 | 0.187 | −0.8362 | 0.0166 |
| 23 | 0.5235 | −0.5222 | 0.0358 |
| 24 | 0.1997 | −0.8173 | 0.0179 |
| 25 | 0.2822 | −0.8367 | 0.0235 |
| 26 | 0.5721 | −0.471 | 0.0417 |
| 27 | 0.1927 | −0.8671 | 0.0184 |
| 28 | 0.416 | −0.4762 | 0.0288 |
| 29 | 0.8128 | −0.2159 | 0.0561 |
| 30 | 0.5524 | −0.3866 | 0.0388 |
| 31 | 0.4501 | −0.4579 | 0.0316 |
| 32 | 0.5187 | −0.4265 | 0.0358 |
| Method | A (µm/s) | B (µm) | C (V) | MRR (mm3/min) | Ra (µm) | TWR | Comp. Time (s) |
|---|---|---|---|---|---|---|---|
| PR-WSMO-GWO | 3.55 | 0.158 | 80 | 0.0126 | 0.3892 | 0.7042 | 1.03886 |
| TOPSIS-PR-GWO | 3.9578 | 0.1 | 80 | 0.0134 | 0.3245 | 0.6367 | 1.02534 |
| Improvement % | - | - | - | 6.35 | 16.62 | 9.58 | 1.3 |
| PR-WSMO-GWO | 3.55 | 0.158 | 80 | 0.0126 | 0.3892 | 0.7042 | 1.03886 |
| MABAC-PR-GWO | 3.8578 | 0.1 | 80 | 0.01232 | 0.3224 | 0.6375 | 1.00352 |
| Improvement % | - | - | - | -2.22 | 17.16 | 9.47 | 3.4 |
| PR-WSMO-GWO | 3.55 | 0.158 | 80 | 0.0126 | 0.3892 | 0.7042 | 1.03886 |
| COPRAS-PR-GWO | 3.8578 | 0.1 | 80 | 0.01232 | 0.3224 | 0.6375 | 1.01936 |
| Improvement % | - | - | - | -2.22 | 17.16 | 9.47 | 1.88 |
| Method | Parametric Combination | Normalized Response Values | Sum | ||||
|---|---|---|---|---|---|---|---|
| A | B | C | MRR | Ra | TWR | ||
| PR-WSMO-GWO | 3.55 | 0.158 | 80 | 0.1959 | 0.988 | 0.9373 | 2.1212 |
| TOPSIS-PR-GWO | 3.9578 | 0.1 | 80 | 0.2122 | 0.9996 | 0.9631 | 2.1749 |
| MABAC-PR-GWO | 3.8578 | 0.1 | 80 | 0.1902 | 1 | 0.9628 | 2.153 |
| COPRAS-PR-GWO | 3.8578 | 0.1 | 80 | 0.1902 | 1 | 0.9628 | 2.153 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Das, P.P. A Hybrid MCDM-Grey Wolf Optimizer Approach for Multi-Objective Parametric Optimization of μ-EDM Process. Eng. Proc. 2023, 59, 112. https://doi.org/10.3390/engproc2023059112
Das PP. A Hybrid MCDM-Grey Wolf Optimizer Approach for Multi-Objective Parametric Optimization of μ-EDM Process. Engineering Proceedings. 2023; 59(1):112. https://doi.org/10.3390/engproc2023059112
Chicago/Turabian StyleDas, Partha Protim. 2023. "A Hybrid MCDM-Grey Wolf Optimizer Approach for Multi-Objective Parametric Optimization of μ-EDM Process" Engineering Proceedings 59, no. 1: 112. https://doi.org/10.3390/engproc2023059112






