Numerical Analysis of Lid-Driven Cavity Flow Induced by Triangular Obstacles †
Abstract
:1. Introduction
2. Literature Review and Objectives
3. Methodology
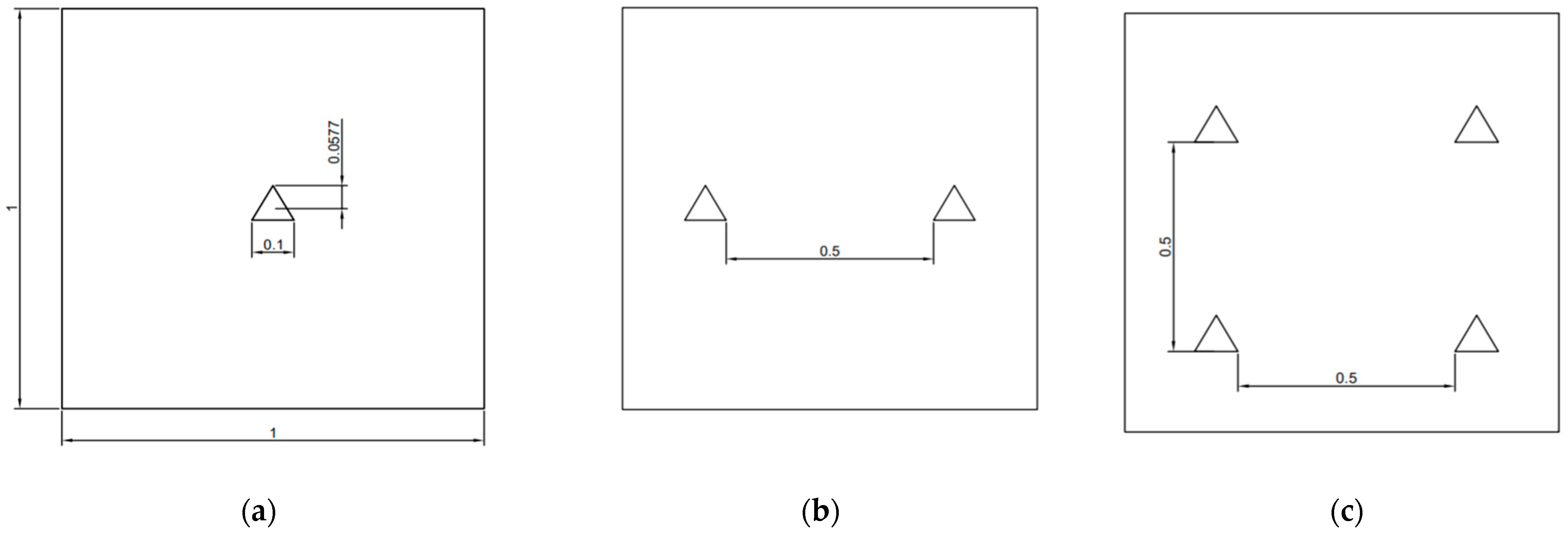
3.1. Physical Model and Mathematical Formulation
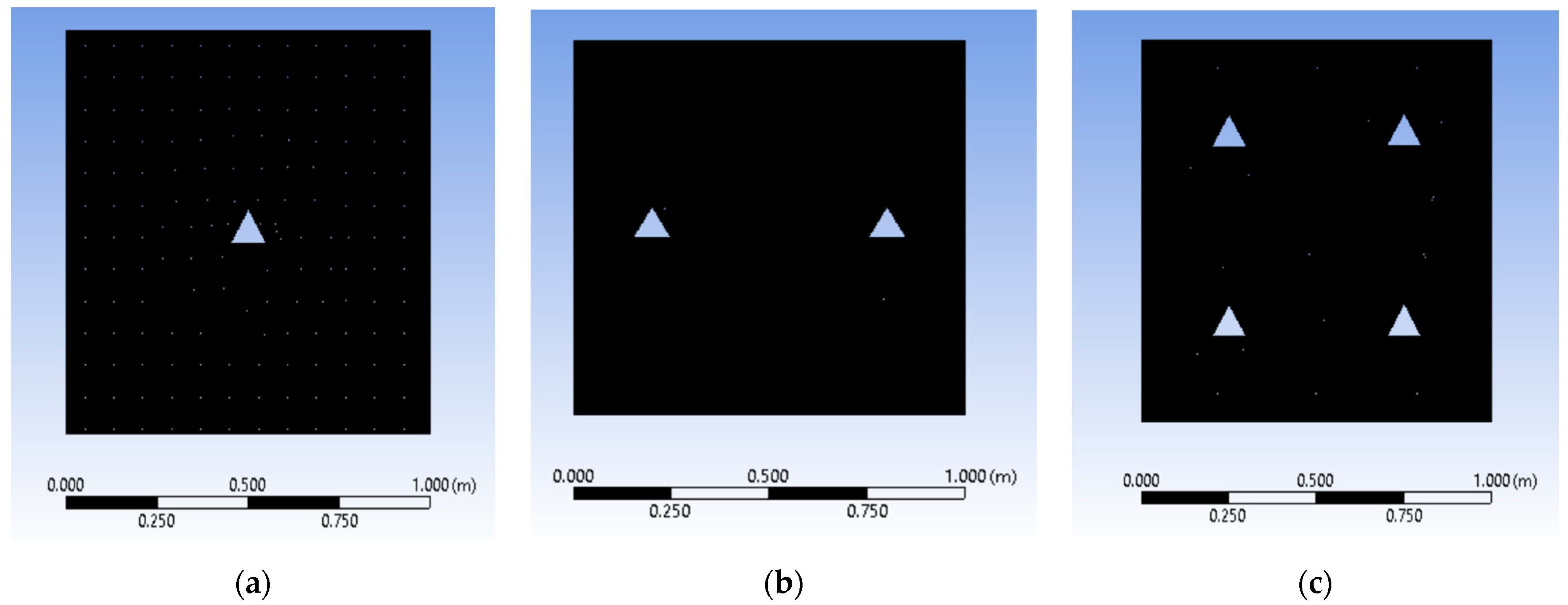
3.2. Numerical Methodology and Grid Sensitivity Analysis
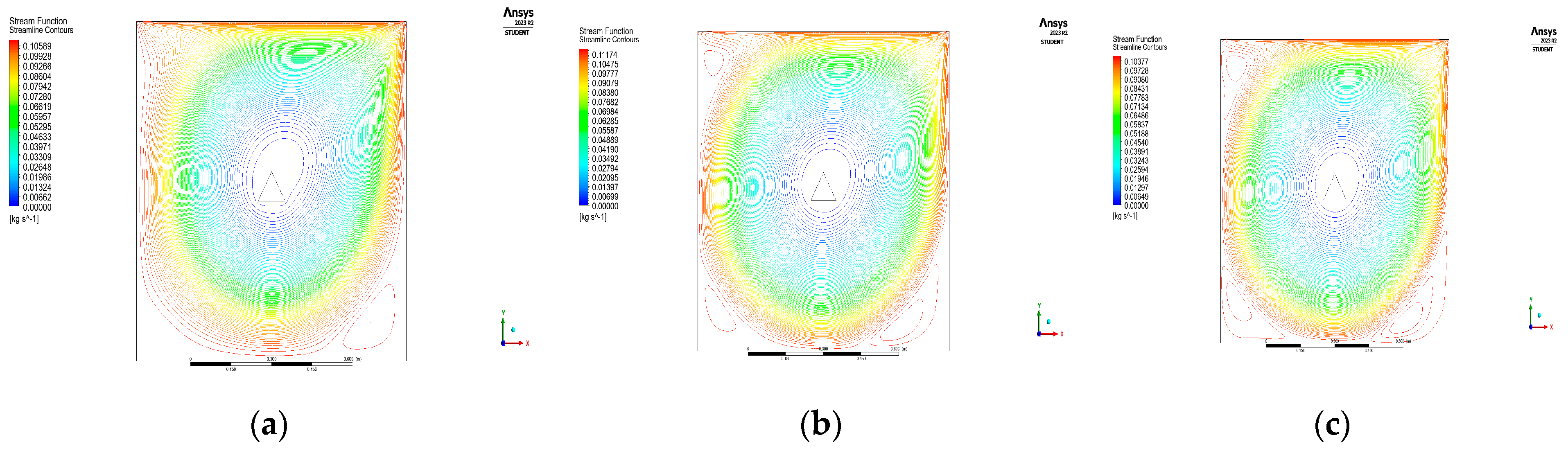
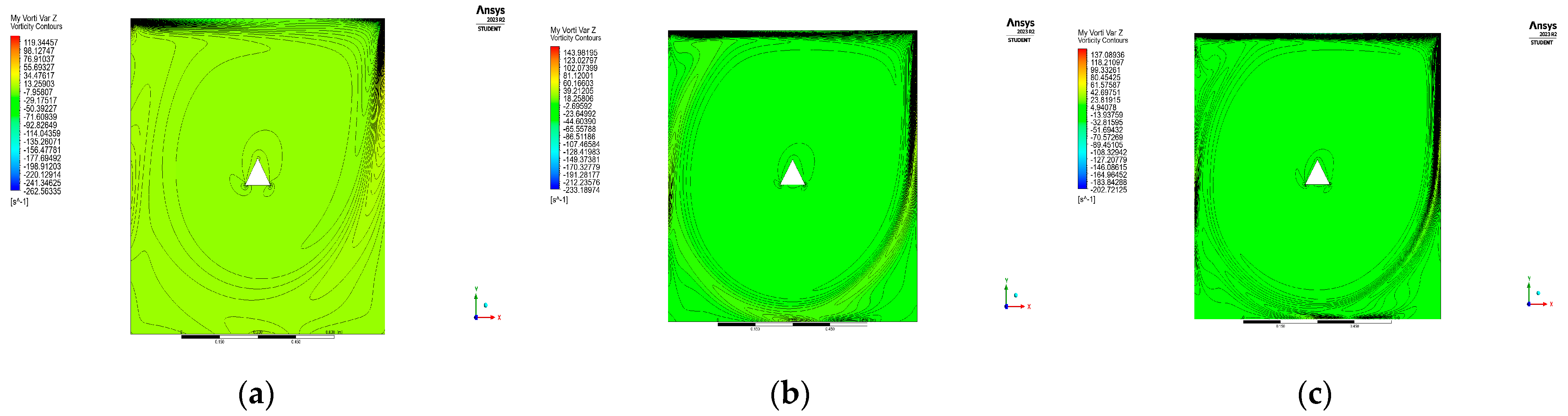
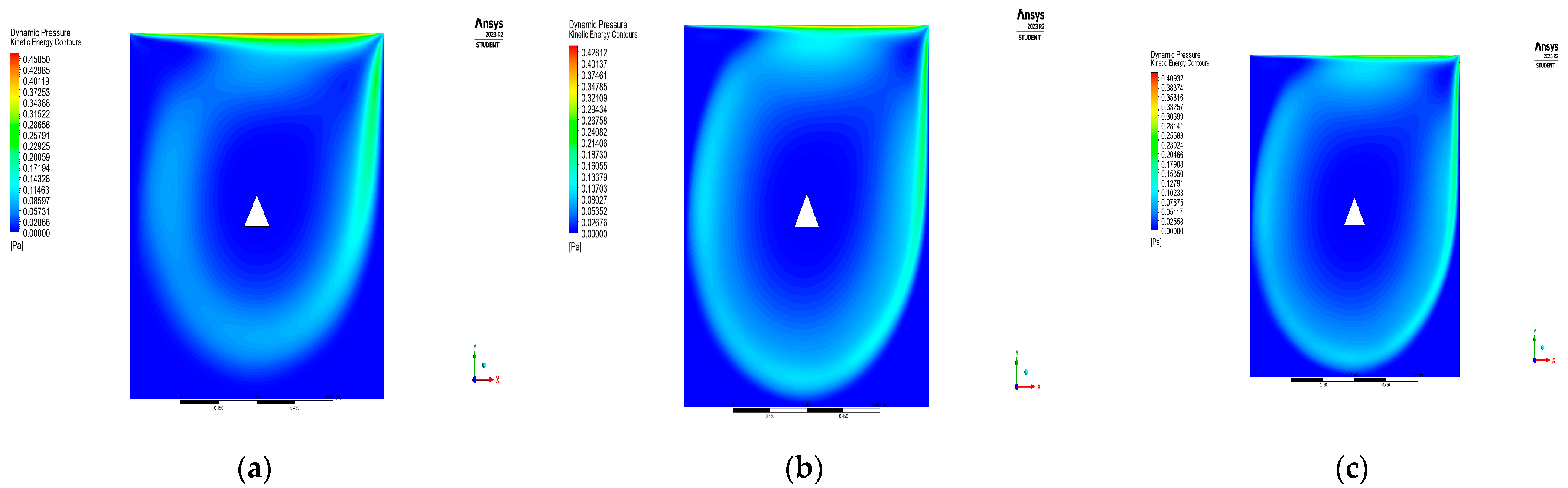
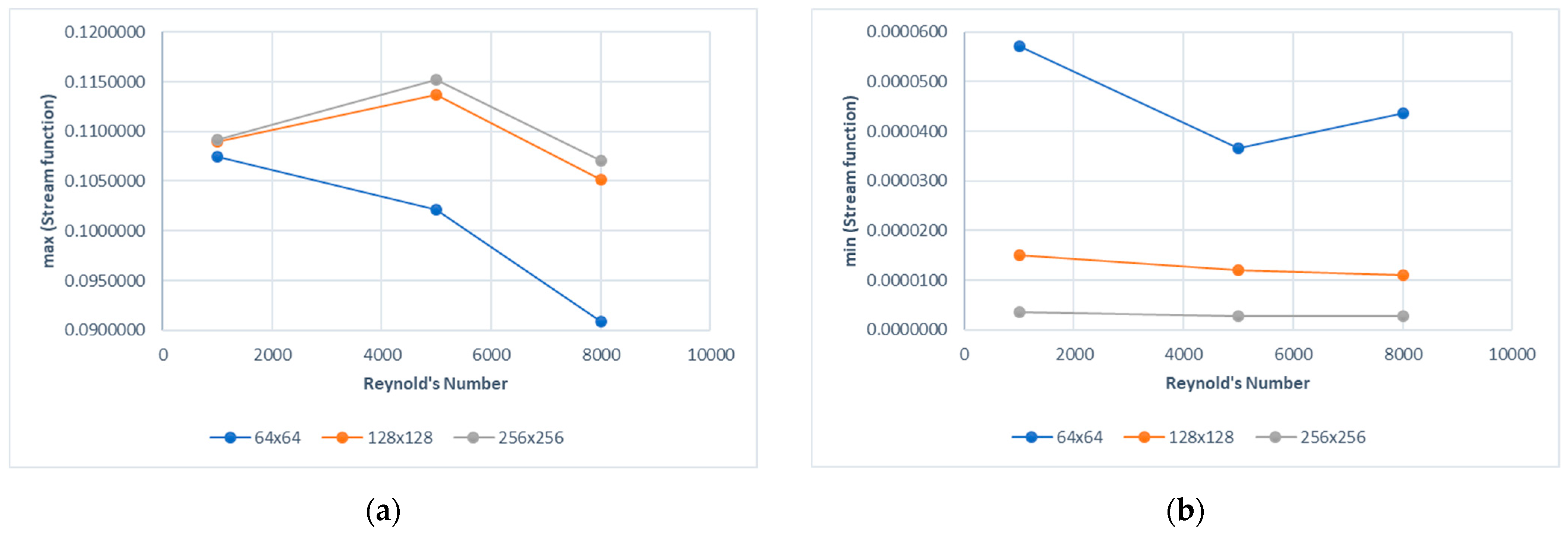
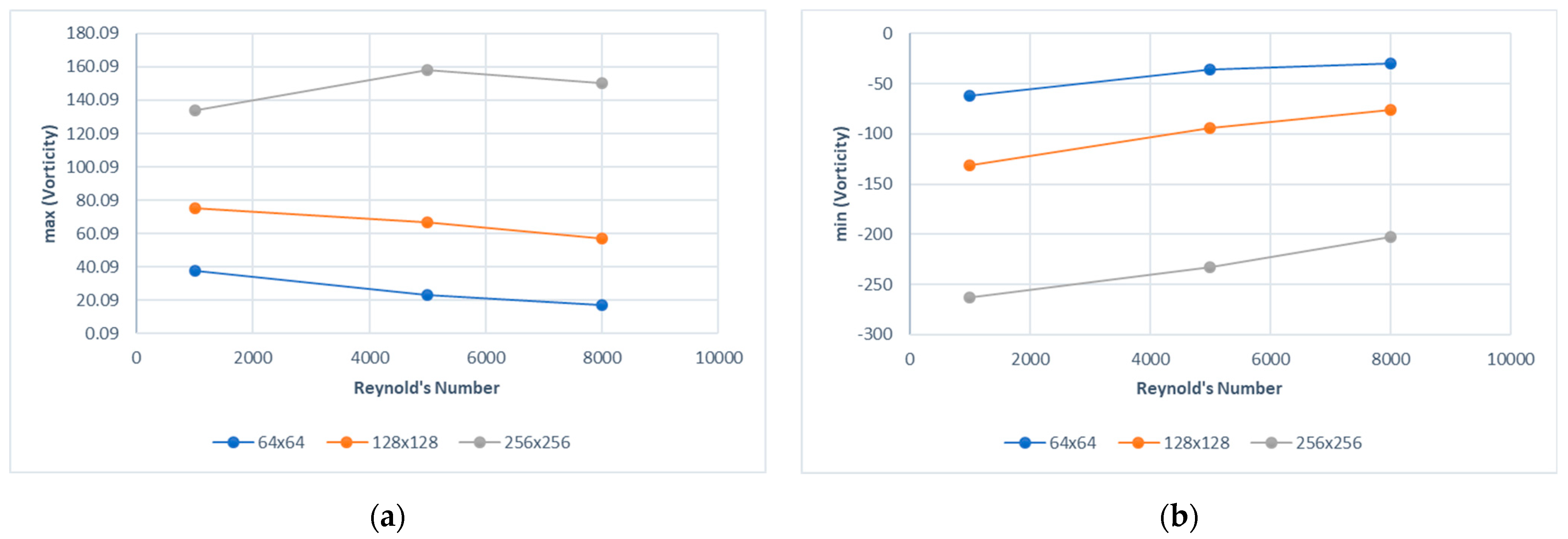
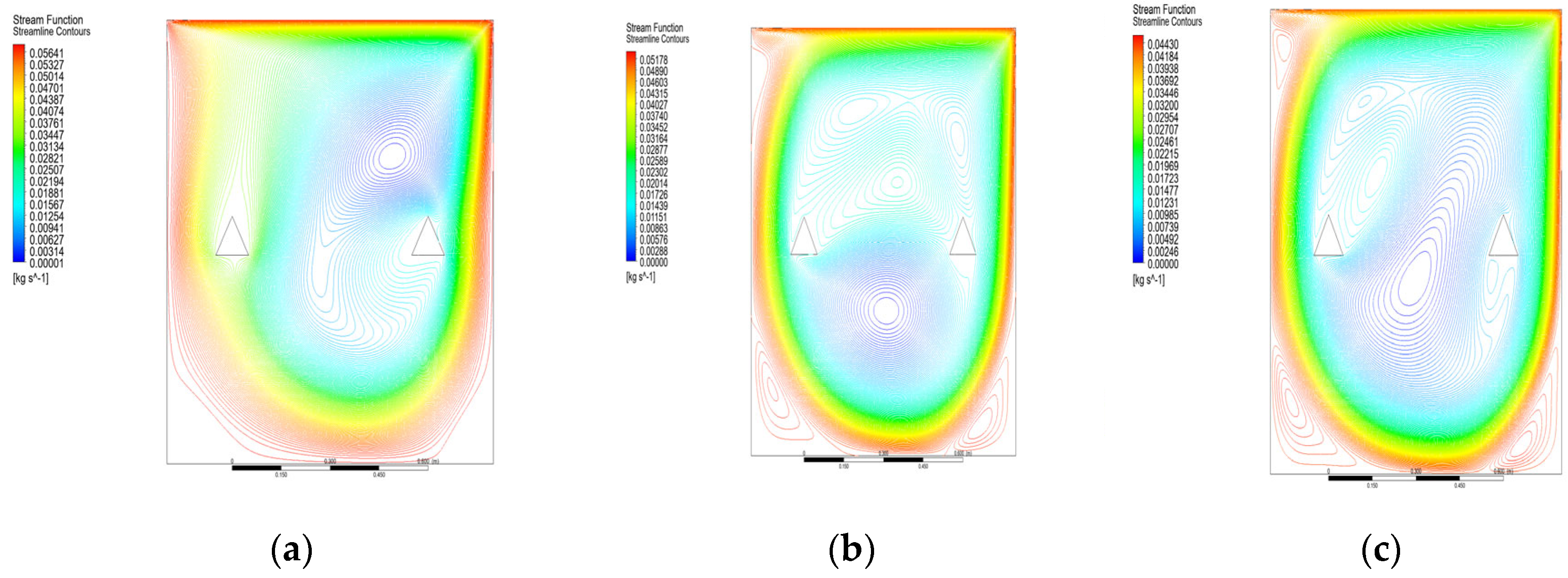
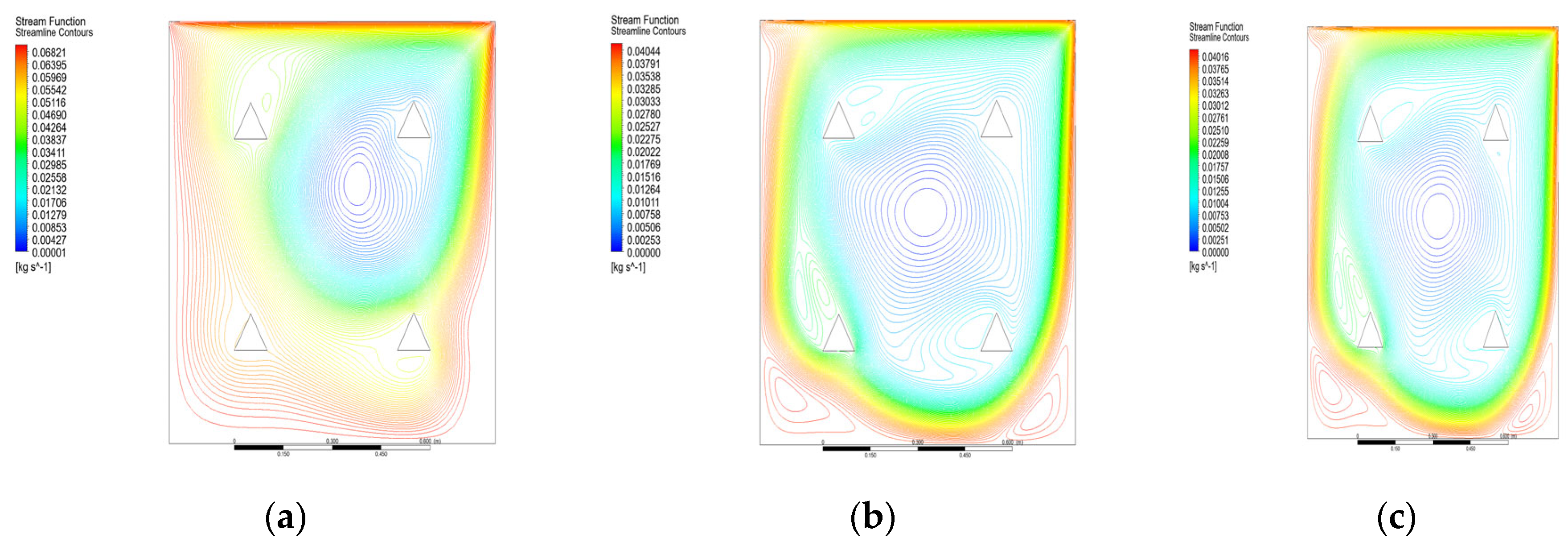
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bhopalam, S.R.; Perumal, D.A.; Yadav, A.K. Computational appraisal of fluid flow behavior in two-sided oscillating lid-driven cavities. Int. J. Mech. Sci. 2021, 196, 1–15. [Google Scholar] [CrossRef]
- Bhopalam, S.R.; Perumal, D.A. Numerical analysis of fluid flows in L-Shaped cavities using Lattice Boltzmann method. Appl. Eng. Sci. 2020, 3, 1–14. [Google Scholar]
- Rajan, I.; Perumal, D.A. Flow Dynamics of Lid-Driven Cavities with obstacles of various shapes and configurations using the Lattice Boltzmann Method. J. Therm. Eng. 2021, 7, 83–102. [Google Scholar] [CrossRef]
- Perumal, D.A. Lattice Boltzmann Computation of Multiple Solutions in a Double-Sided Square and Rectangular Cavity Flows. Therm. Sci. Eng. Prog. 2018, 6, 48–56. [Google Scholar] [CrossRef]
- Perumal, D.A.; Dass, A.K. Multiplicity of steady solutions in two-dimensional lid driven cavity flows by Lattice Boltzmann method. Comput. Math. Appl. 2011, 61, 3711–3721. [Google Scholar] [CrossRef]
- Xie, B.; Xiao, F. A multi-moment constrained finite volume method on arbitrary unstructured grids for incompressible flows. J. Comput. Phys. 2016, 327, 747–778. [Google Scholar] [CrossRef]
- Zamzamian, K.; Hashemi, M.Y. A novel meshless method for incompressible flow calculations. Eng. Anal. Bound. Elem. 2015, 56, 106–118. [Google Scholar] [CrossRef]
- Jiang, Y.; Mei, L.; Wei, H. A finite element variational multiscale method for incompressible flow. Appl. Math. Comput. 2015, 266, 374–384. [Google Scholar] [CrossRef]
- Perumal, D.A.; Dass, A.K. Application of Lattice Boltzmann method for incompressible viscous flows. Appl. Math. Model. 2011, 37, 4075–4092. [Google Scholar] [CrossRef]
- Ghia, U.; Ghia, K.N.; Shin, C.T. High-resolutions for incompressible flow using the Navier–Stokes equations and a multigrid method. J. Comput. Phys. 1982, 48, 387–411. [Google Scholar] [CrossRef]
- Lin, L.S.; Chen, Y.C.; Lin, C.A. Multi relaxation time lattice Boltzmann simulations of deep lid driven cavity flows at different aspect ratios. Comput. Fluids 2011, 45, 233–240. [Google Scholar] [CrossRef]
- Azwadi, C.S.N.; Rajab, A.; Sofianuddin, A. Four-sided lid driven cavity flow using time splitting method of Adams-Bashforth scheme. Int. J. Automot. Mech. Eng. 2014, 9, 1501–1510. [Google Scholar] [CrossRef]
- Gokhale, F. Lattice Boltzmann simulation of fluid flow in a lid driven cavity. Int. J. Mech. Eng. Robot. 2014, 2, 1–5. [Google Scholar]
- Safdari, A.; Kim, K.C. Lattice Boltzmann simulation of solid particles behavior in a three-dimensional lid-driven cavity flow. Comput. Math. Appl. 2014, 68, 606–621. [Google Scholar] [CrossRef]
- Zhuo, C.; Zhong, C.; Guo, X.; Cao, J. Numerical investigation of four-lid-driven cavity flow bifurcation using the multiple-relaxation-time lattice Boltzmann method. Comput. Fluids 2015, 110, 136–151. [Google Scholar] [CrossRef]
- Perumal, D.A.; Dass, A.K. A review on the development of Lattice Boltzmann computation of Macro fluid flows and Heat Transfer. Alex. Engg J. 2015, 54, 955–971. [Google Scholar] [CrossRef]
- Endang, M.; Eko, P.B.; Yuana, K.A.; Kamal, S. Deendalinto, Simulation of lid-driven cavity with top and bottom moving boundary conditions using implicit finite difference method and staggered grid. AIP Conf. Proc. 2018, 2021, 020002. [Google Scholar]
- Souayeh, B.; Alam, M.W.; Hammami, F.; Hdhiri, N.; Yasin, E. Predicting the unsteady states of 2D and 3D lid-driven cavities induced by a centrally located circle and sphere. Fluid Dyn. Res. 2020, 52, 025507. [Google Scholar] [CrossRef]
- Cazemier, W.; Verstappen, C.P.; Veldman, E.P. Proper orthogonal decomposition and low dimensional model for driven cavity flow. Phys. Fluids 1998, 10, 1685–1699. [Google Scholar] [CrossRef]
- Gouillart, T. Topological mixing of viscous fluids. In Proceedings of the Condensed Matter Seminar, Edinburgh, UK, 5 June 2006. [Google Scholar]
| Grid Size for Re = 1000 | umin | vmin |
|---|---|---|
| 64 × 64 | −0.374630 | −0.635462 |
| 128 × 128 | −0.382873 (2.2%) | −0.668224 (5.155%) |
| Ψmin | xmin | ymin | Ψmax | xmax | ymax |
|---|---|---|---|---|---|
| 0.000004 | 0.562781 | 0.593031 | 0.109204 | 0.87188 | 0.113281 |
| umin | ymin | vmax | xmax | vmin | xmin | |
|---|---|---|---|---|---|---|
| Present Work | −0.384500 | 0.167969 | 0.377915 | 0.152318 | −0.674865 | 0.972656 |
| Souyayeh et al. [18] | −0.388300 | 0.169800 | 0.376800 | 0.156400 | 0.5270000 | 0.908800 |
| Gouillart and Thiffeault [20] | −0.382800 | 0.171900 | 0.370900 | 0.156300 | −0.515500 | 0.906300 |
| Cazemier et al. [19] | −0.386900 | 0.180000 | 0.375600 | 0.150000 | −0.526300 | 0.910000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hegde, S.N.; Bendre, N.L.; Perumal, D.A. Numerical Analysis of Lid-Driven Cavity Flow Induced by Triangular Obstacles. Eng. Proc. 2023, 59, 113. https://doi.org/10.3390/engproc2023059113
Hegde SN, Bendre NL, Perumal DA. Numerical Analysis of Lid-Driven Cavity Flow Induced by Triangular Obstacles. Engineering Proceedings. 2023; 59(1):113. https://doi.org/10.3390/engproc2023059113
Chicago/Turabian StyleHegde, Sumanth N., Nihal L. Bendre, and D. Arumuga Perumal. 2023. "Numerical Analysis of Lid-Driven Cavity Flow Induced by Triangular Obstacles" Engineering Proceedings 59, no. 1: 113. https://doi.org/10.3390/engproc2023059113






