Investigation on the Acoustic Performance of Micro-Perforated Panel Integrated Coiled-Up Space Acoustic Absorber †
Abstract
:1. Introduction
2. Methodology
2.1. Geometric Model
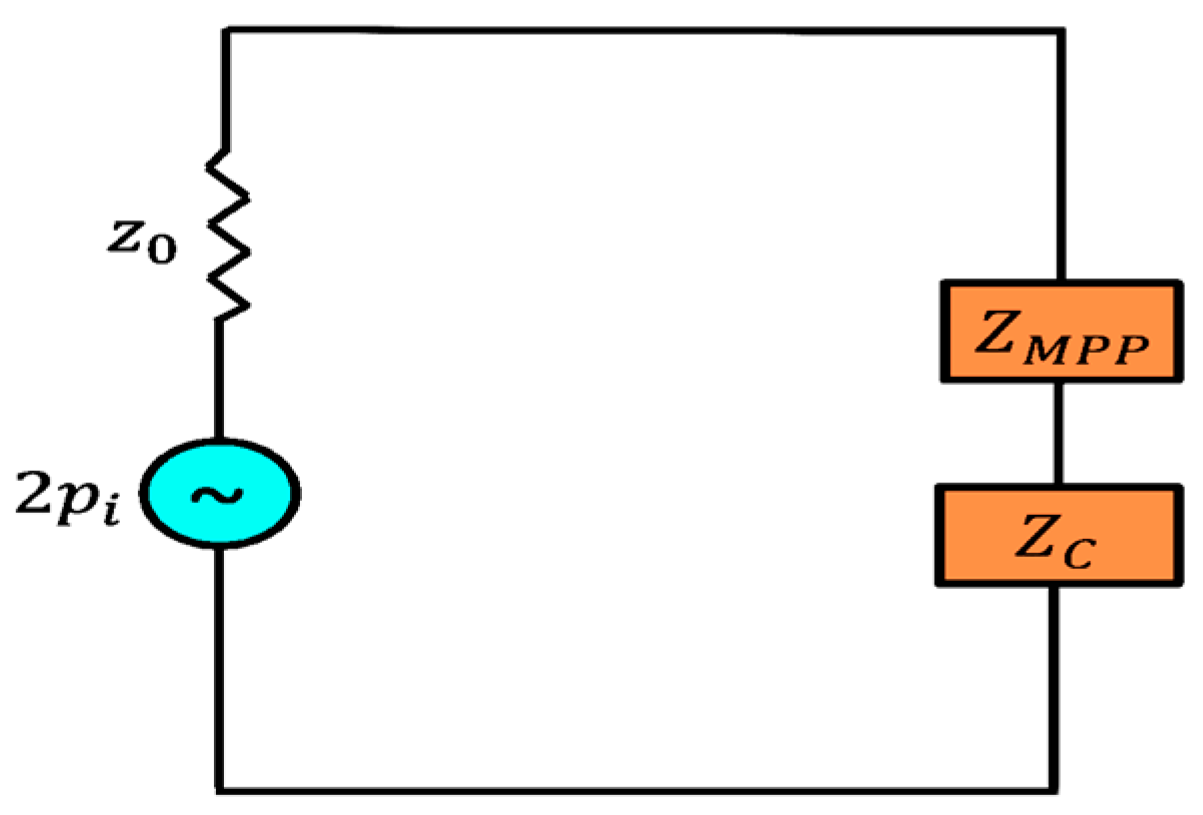
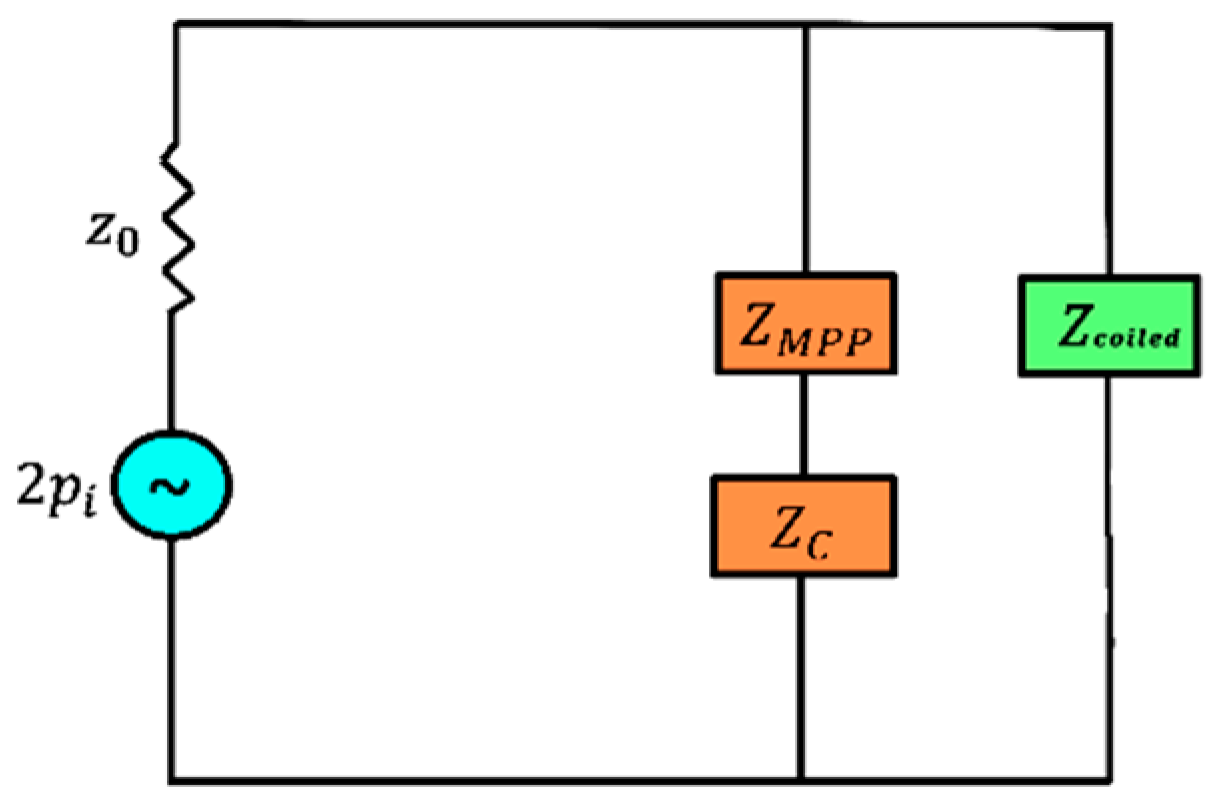
2.2. Numerical Model
2.3. Analytical Model
- Here, the function F(x) is
- The normalized specific acoustic reactance is
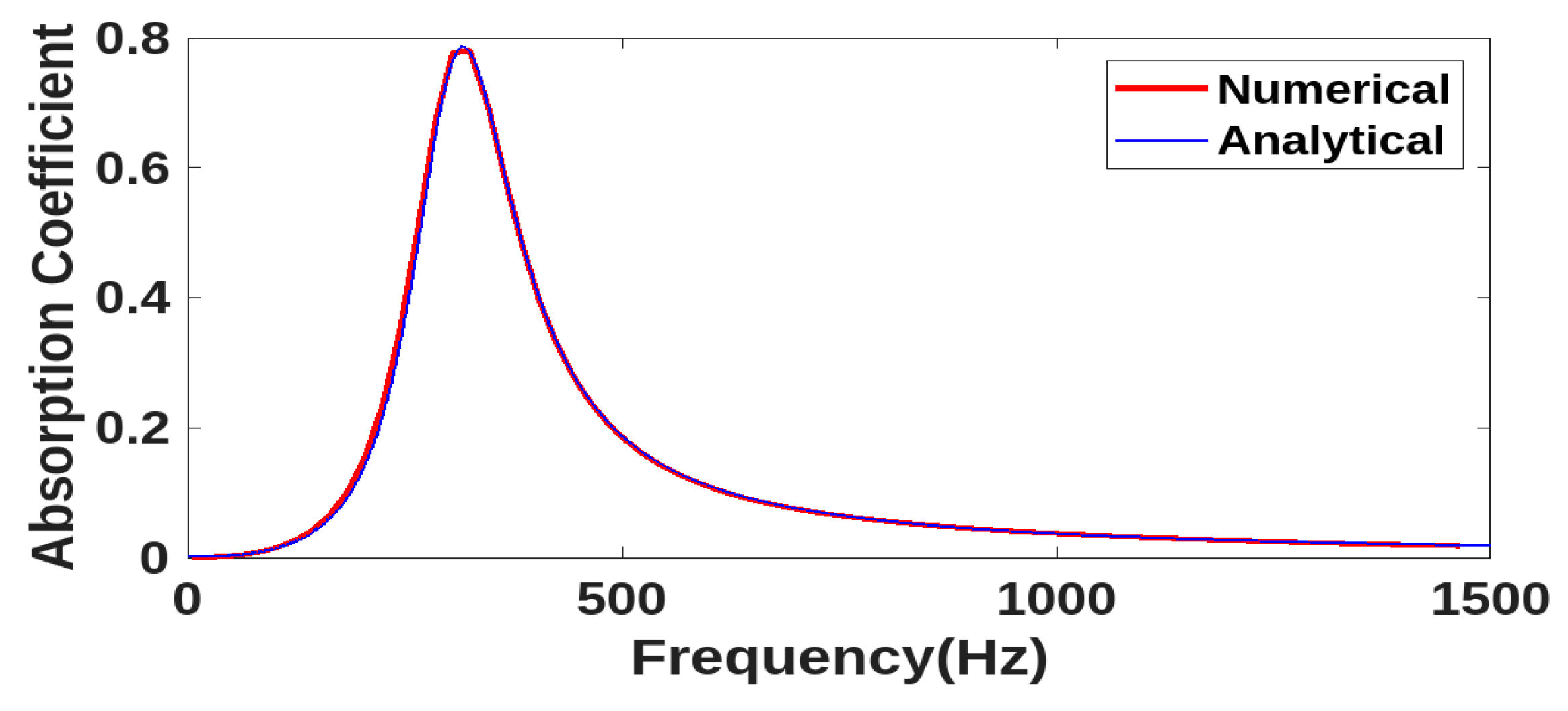
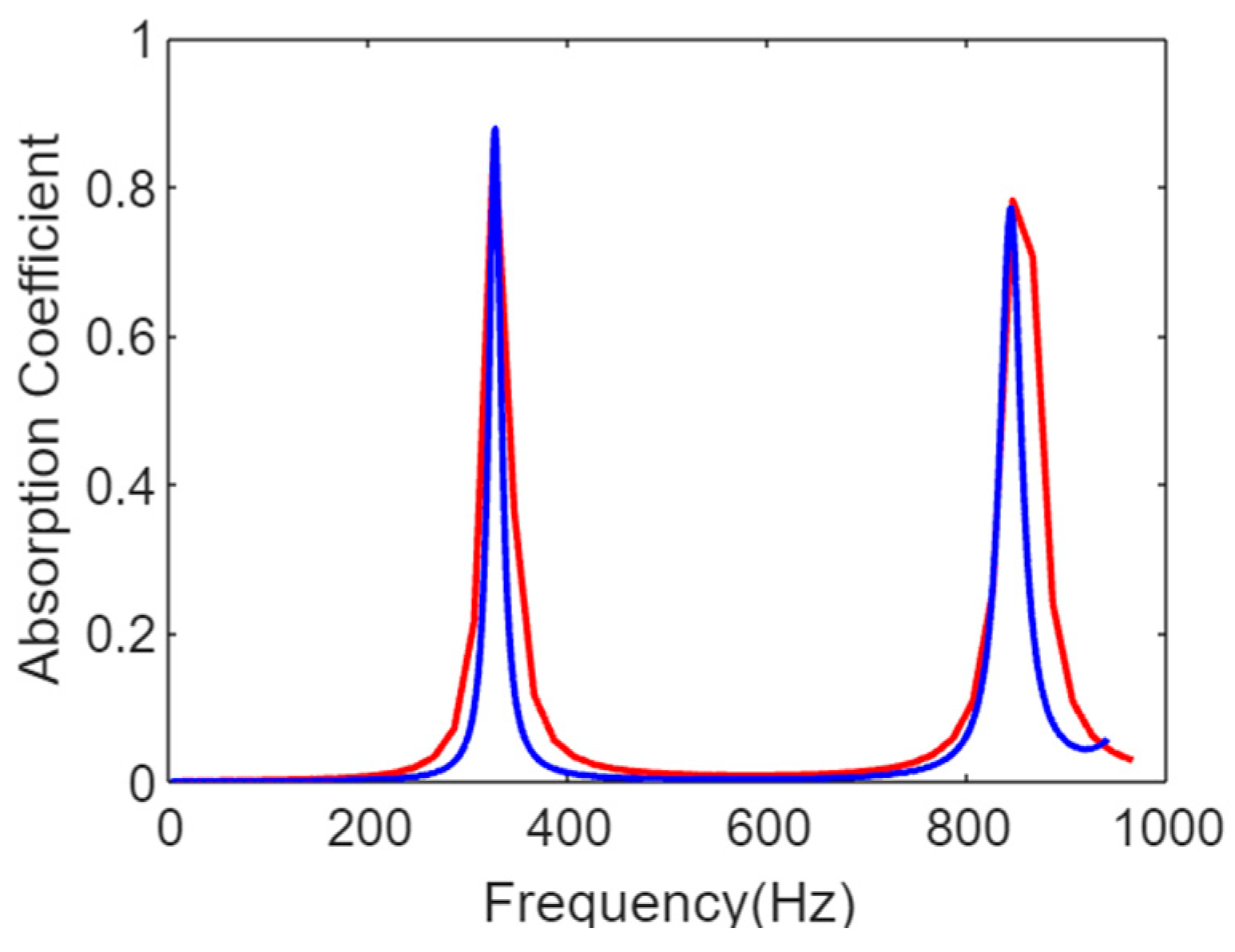
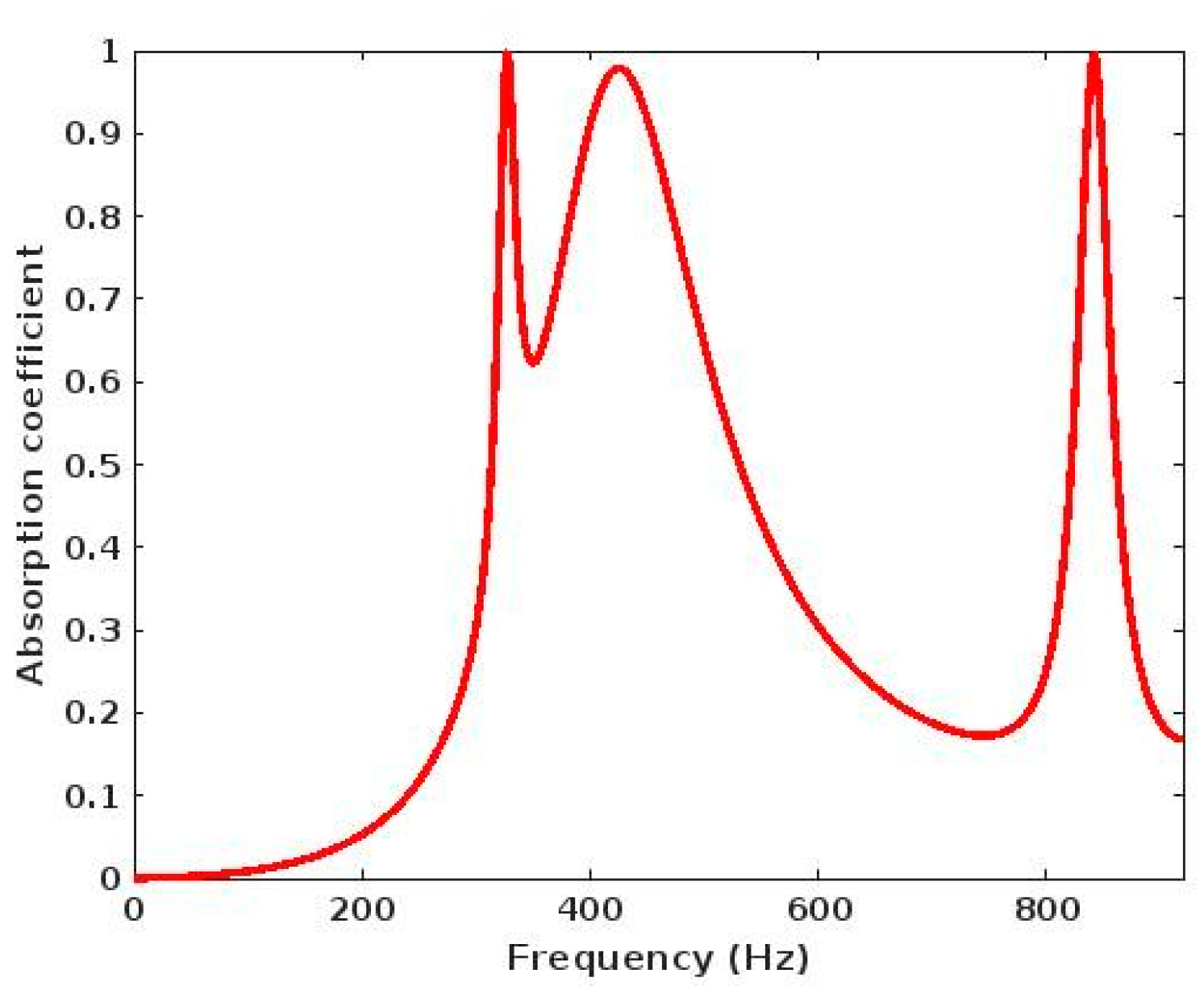
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Leventhall, H.G. Low frequency noise and annoyance. Noise Health 2004, 6, 59–72. [Google Scholar]
- Berglund, B.; Hassmen, P.; Job, R.F. Sources and effects of low frequency noise. J. Acoust. Soc. Am. 1996, 99, 2985–3002. [Google Scholar] [CrossRef] [PubMed]
- Araujo, A.; Neto, P.F.; Torres, S.L.; Remoald, P. Low frequency noise and its main effects on human health-A review of the literaturebetween 2016 and 2019. Appl. Sci. 2020, 10, 5205. [Google Scholar] [CrossRef]
- Miedema, H.; Oudshoorn, C. Annoyance from transportation noise: Relationships with exposure metrics DNL and DENL and their confidence intervals. Environ. Health Perspect. 2001, 109, 409–416. [Google Scholar] [CrossRef] [PubMed]
- Mehdi, M.R.; Kim, M.; Seong, J.C.; Arsalan, M.H. Spatio-temporal patterns of road traffic noise pollution in Karachi, Pakistan. Environ. Int. 2011, 37, 97–104. [Google Scholar] [CrossRef] [PubMed]
- Licitra, G.; Fredianelli, L.; Petri, D.; Vigotti, M.A. Annoyance evaluation due to overall railway noise and vibration in Pisa urban areas. Sci. Total Environ. 2016, 568, 1315–1325. [Google Scholar] [CrossRef] [PubMed]
- Mahesh, K.; Mini, R.S. Investigation on the Acoustic Performance of Multiple Helmholtz Resonator Configurations. Acoust. Aust. 2021, 49, 355–369. [Google Scholar] [CrossRef]
- Mahesh, K.; Mini, R.S. Theoretical investigation on the acoustic performance of Helmholtz resonator integrated microperforated panel absorber. Appl. Acout. 2021, 178, 108012. [Google Scholar] [CrossRef]
- Pavan, G.; Singh, S. Near-perfect sound absorptions in low-frequencies by varying compositions of porous labyrinthine acoustic metamaterial. Appl. Acoust. 2022, 198, 108974. [Google Scholar] [CrossRef]
- Dratva, J.; Phuleria, H.C.; Foraster, M.; Gaspoz, J.M.; Keidel, D.; Künzli, N.; Liu, L.-J.S.; Pons, M.; Zemp, E.; Gerbase, M.W. Transportation noise and blood pressure in a population-based sample of adults. Environ. Health Perspect. 2012, 120, 50–55. [Google Scholar] [CrossRef] [PubMed]
- Babisch, W.; Ising, H.; Gallacher, J. Health status as a potential effect modifier of the relation between noise annoyance and incidence of ischaemic heart disease. Occup. Environ. Med. 2003, 60, 739–745. [Google Scholar] [CrossRef] [PubMed]
- Muzet, A. Environmental noise, sleep and health. Sleep Med. Rev. 2007, 11, 135–142. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Chung, Y.; Wang, C.; Lo, W.; Liu, C.; Yu, C.; Chang, I.; Lin, T. Ultrathin arch-like labyrinthine acoustic metasurface for low-frequency sound absorption. Appl. Acoust. 2023, 202, 109142. [Google Scholar] [CrossRef]
- Langfeldt, F.; Khatokar, A.; Gleine, W. Plate-type acoustic metamaterials with integrated Helmholtz resonators. Appl. Acoust. 2022, 199, 109019. [Google Scholar] [CrossRef]
- Lu, Q.; Li, X.; Zhang, X.; Lu, M.; Chen, Y. Perspective: Acoustic Metamaterials in Future Engineering. Engineering 2022, 17, 22–30. [Google Scholar] [CrossRef]
- Gaafer, F.N. Broadband Low-Frequency Sound Absorption via a Hexagonal Acoustic Metamaterial in the Honeycomb Structure. Kuwait J. Sci. 2022, 49, 1–11. [Google Scholar] [CrossRef]
- Chang, L.; Jiang, A.; Rao, M.; Ma, F.; Huang, H.; Zhu, Z.; Zhang, Y.; Wu, Y.; Li, B.; Hu, Y. Progress of low-frequency sound absorption research utilizing intelligent materials and acoustic metamaterials. RSC Adv. 2021, 11, 37784–37800. [Google Scholar] [CrossRef] [PubMed]
- Hongyu, C.; Chengtao, L.; Haoming, H. Research on Low-Frequency Noise Control Based on Fractal Coiled Acoustic Metamaterials. Shock Vib. 2022, 2022, 1–14. [Google Scholar]
- Wolkesson, M. Evaluation of Impedance Tube Methods—A Two Microphone In-Situ Method for Road Surfaces and the Three Microphone Transfer Function Method for Porous Materials. Master’s Thesis, Chalmers University of Technology, Goteborg, Sweden, 2013. [Google Scholar]
- Mahesh, K.; Mini, R.S. Numerical Investigation on the Absorption Characteristics of Helmholtz Resonator Based Absorber with Neck Opening on the Wall, In Proceedings of the International Conference on Emerging Trends in Engineering Yukthi-2021, Kozhikode, India, 24–26 September 2021.
- Maa, D.Y. Theory and design of microperforated panel sound-absorbing constructions. Sci. Sin. 1975, 18, 55–71. [Google Scholar]




| Width Channel 1 | Length Channel 1 | Width Channel 2 | Length Channel 2 | Height | Wall Thickness |
|---|---|---|---|---|---|
| 11 mm | 264 mm | 8 mm | 102 mm | 12 mm | 3 mm |
| Diameter of Panel | Thickness of Panel | Diameter of Perforation | Cavity Height | Porosity |
|---|---|---|---|---|
| 100 mm | 1 mm | 1 mm | 40 mm | 0.08 |
| Coiled Cavity | Width (mm) | Length (mm) |
|---|---|---|
| 1 | 11 | 264 |
| 2 | 8 | 102 |
| Panel | Thickness (mm) | Diameter of Holes (mm) | Porosity of Panel |
|---|---|---|---|
| 1 | 2.7 | 1.3 | 0.018 |
| 2 | 3.8 | 1.7 | 0.015 |
| 3 | 1.5 | 1 | 0.02 |
| 4 | 1.3 | 2.5 | 0.006 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krishna, D.S.G.; Leena, P.A.; Karottuthundathil, A.; Mohammed, A.; Kavungal, M.; Sahadevan, M.R. Investigation on the Acoustic Performance of Micro-Perforated Panel Integrated Coiled-Up Space Acoustic Absorber. Eng. Proc. 2023, 59, 168. https://doi.org/10.3390/engproc2023059168
Krishna DSG, Leena PA, Karottuthundathil A, Mohammed A, Kavungal M, Sahadevan MR. Investigation on the Acoustic Performance of Micro-Perforated Panel Integrated Coiled-Up Space Acoustic Absorber. Engineering Proceedings. 2023; 59(1):168. https://doi.org/10.3390/engproc2023059168
Chicago/Turabian StyleKrishna, Damodaran Sanalkumar Govind, Parvathy Arun Leena, Abhinav Karottuthundathil, Ashidha Mohammed, Mahesh Kavungal, and Mini Rema Sahadevan. 2023. "Investigation on the Acoustic Performance of Micro-Perforated Panel Integrated Coiled-Up Space Acoustic Absorber" Engineering Proceedings 59, no. 1: 168. https://doi.org/10.3390/engproc2023059168






