Decentralised Voltage Regulation through Optimal Reactive Power Flow in Distribution Networks with Dispersed Generation
Abstract
1. Introduction
2. Literature Review
2.1. Voltage Regulation in Modern Distribution Networks
2.2. Optimal Reactive Power Flow
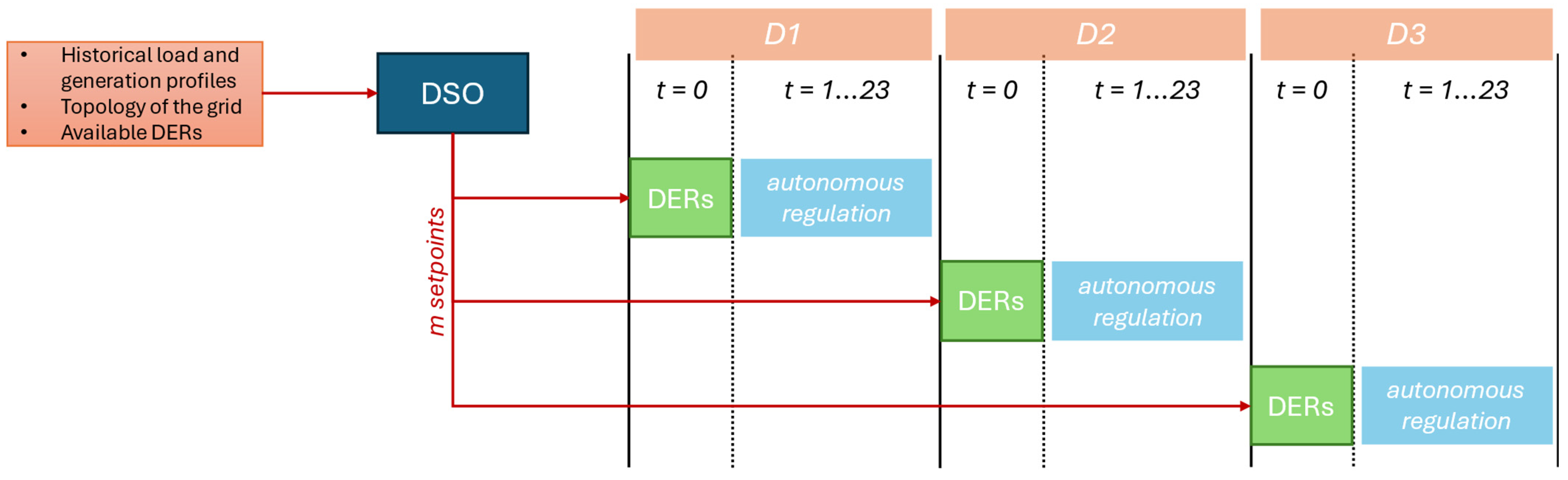
3. Methodology
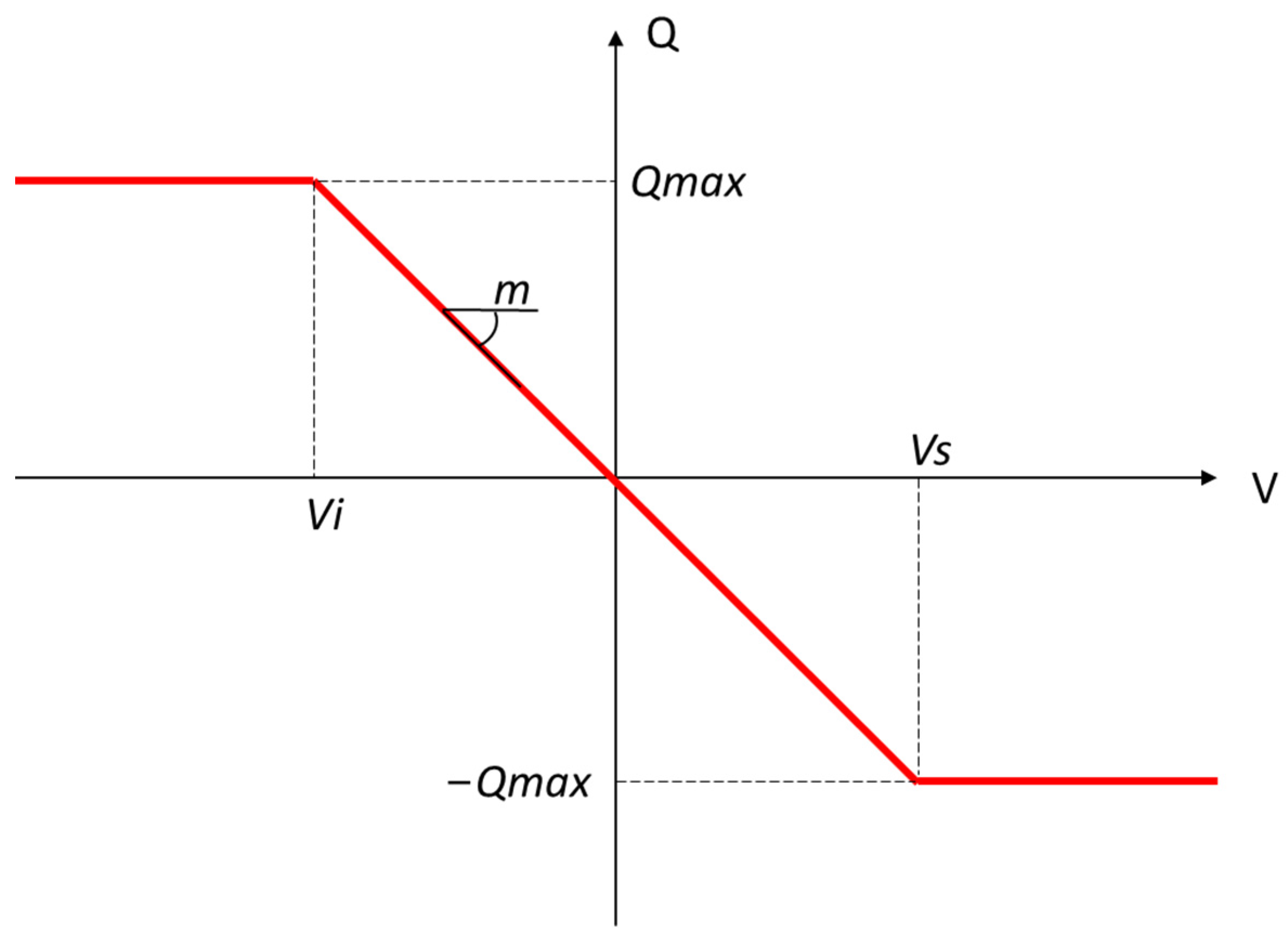
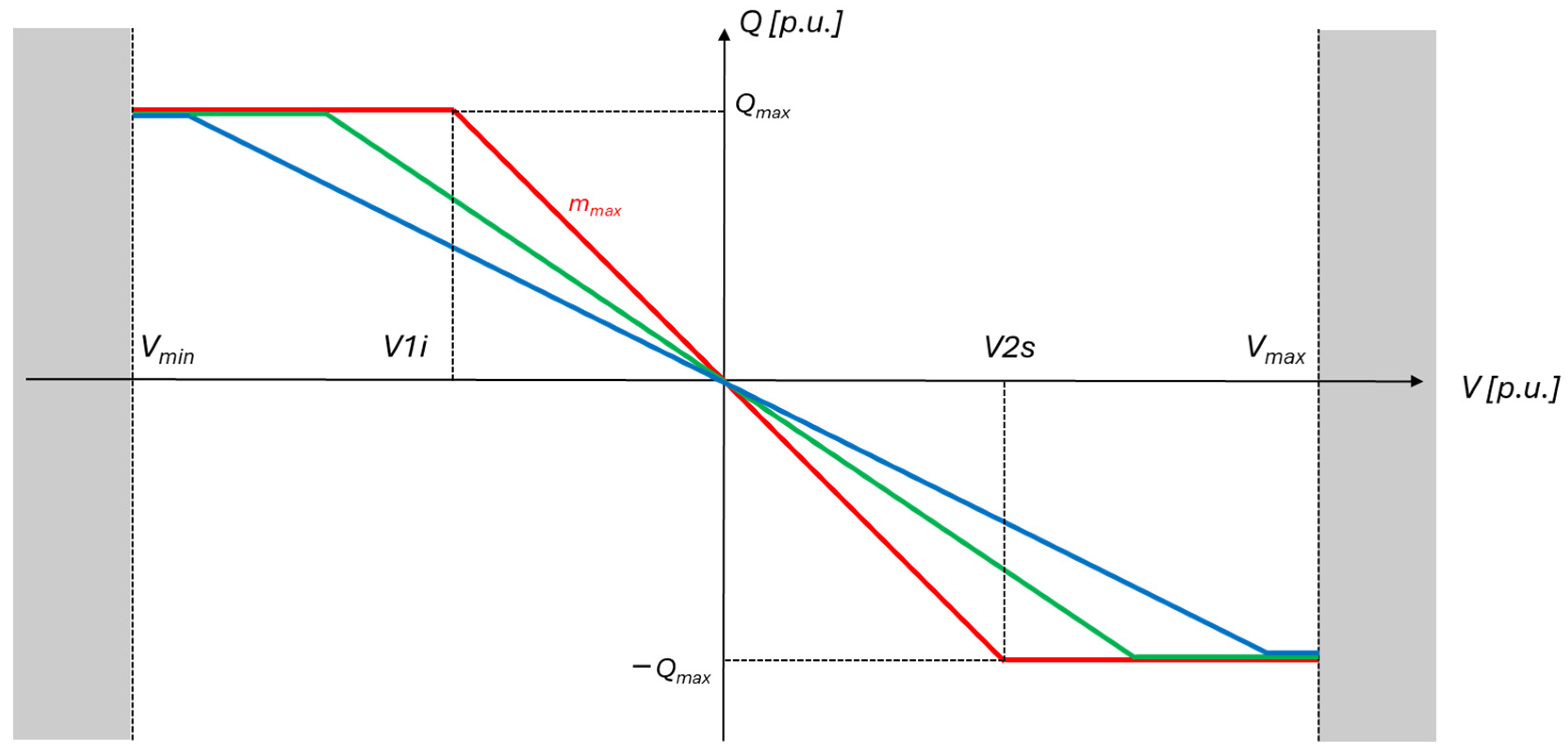
3.1. The Q(V) Control Law
3.2. The Mathematical Model
- is the set of all nodes of the grid;
- is the active power injected in the bth bus;
- is the active power required by the bth bus;
- is the reactive power injected in the bth bus;
- is the reactive power required by the bth node;
- , are the magnitudes of the nodal voltage in p.u.;
- are the angles of the nodal voltage in p.u.;
- is the magnitude of the kmth element of the nodal admittance matrix;
- is the angle of the kmth element of the nodal admittance matrix.
- is the set of nodes of the grid at which the DERs are connected;
- is a suitable penalty factor;
- is the angular coefficient of the gth distributed generator.
4. Case Studies and Numerical Results
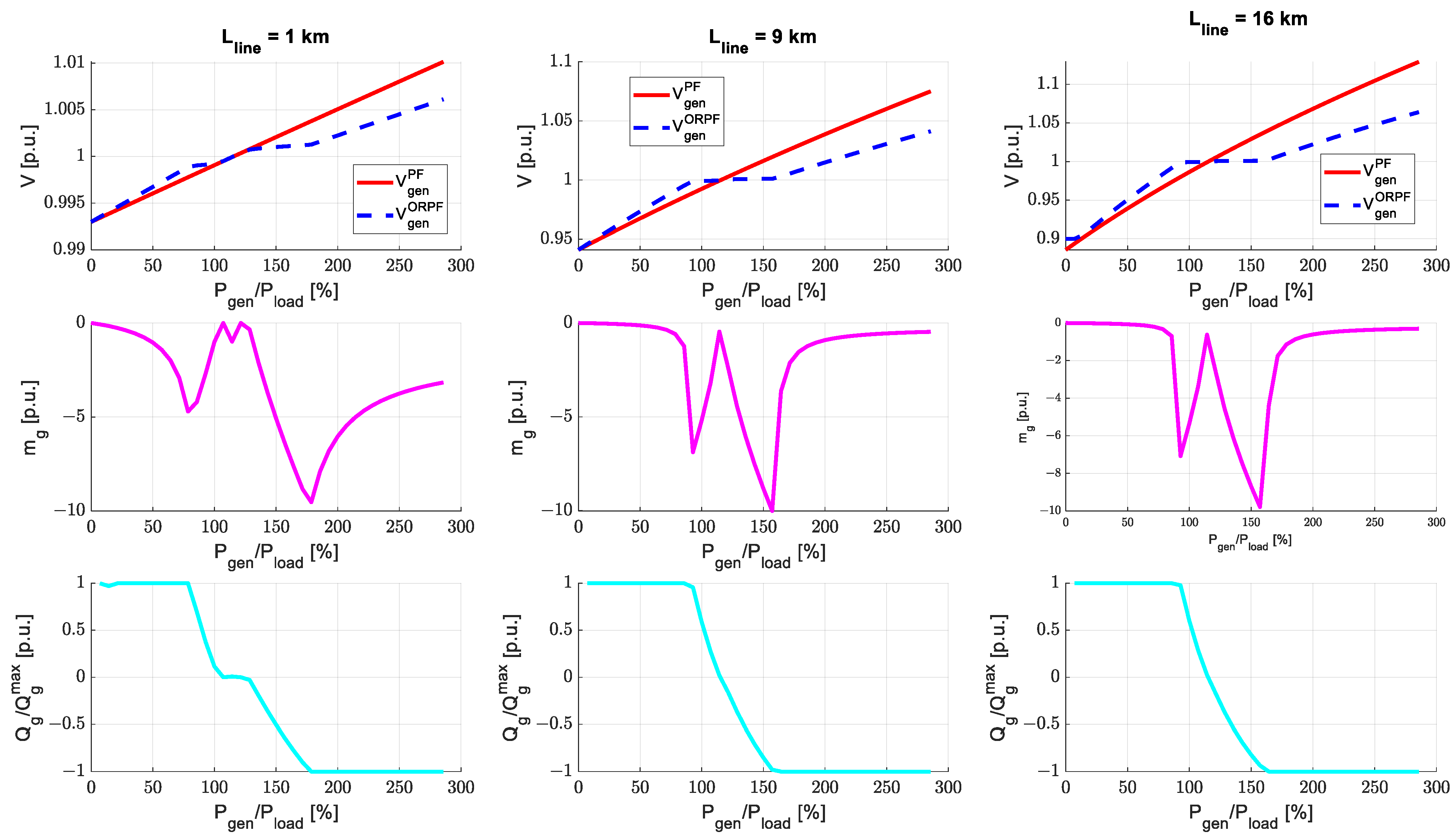
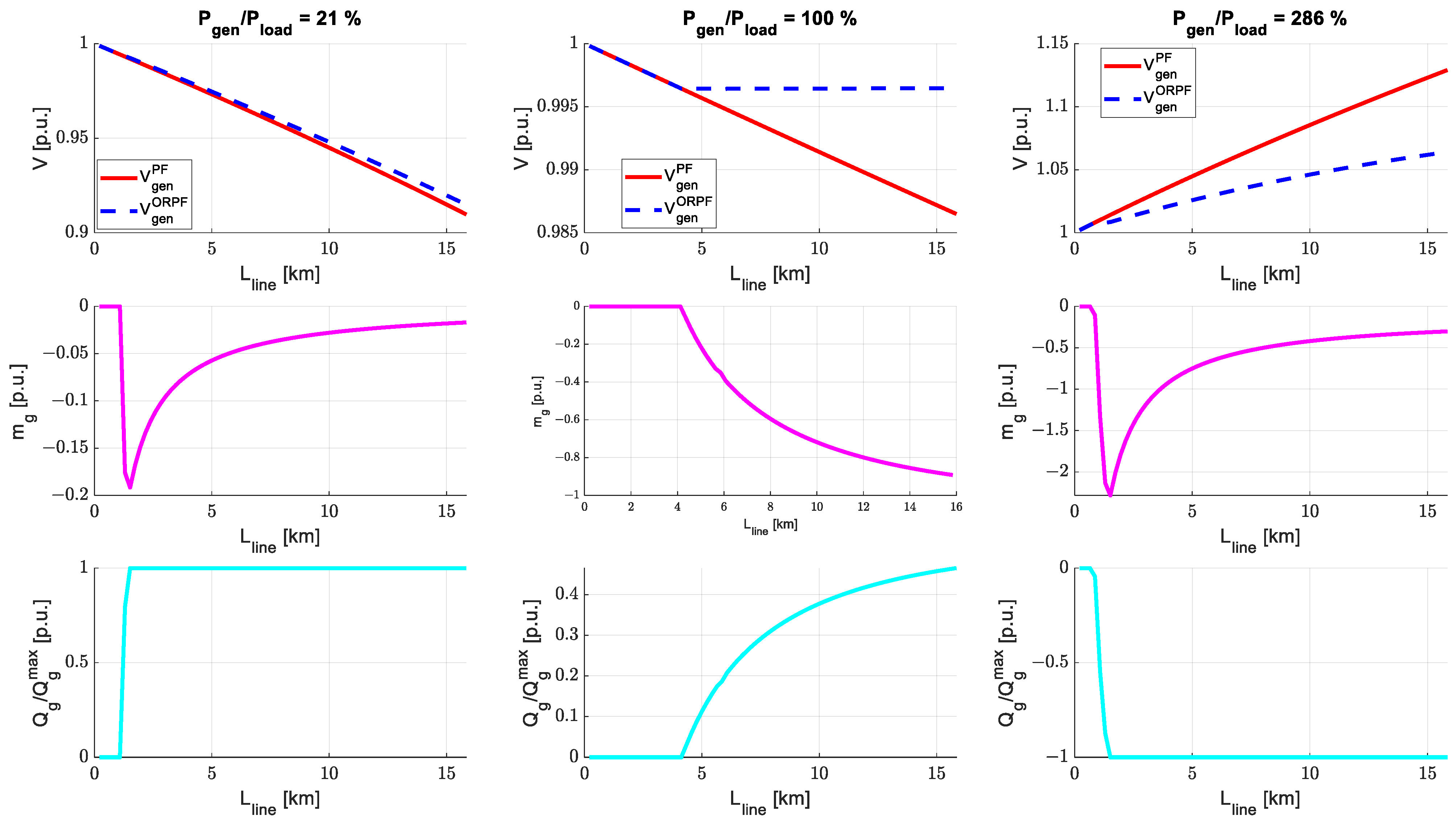
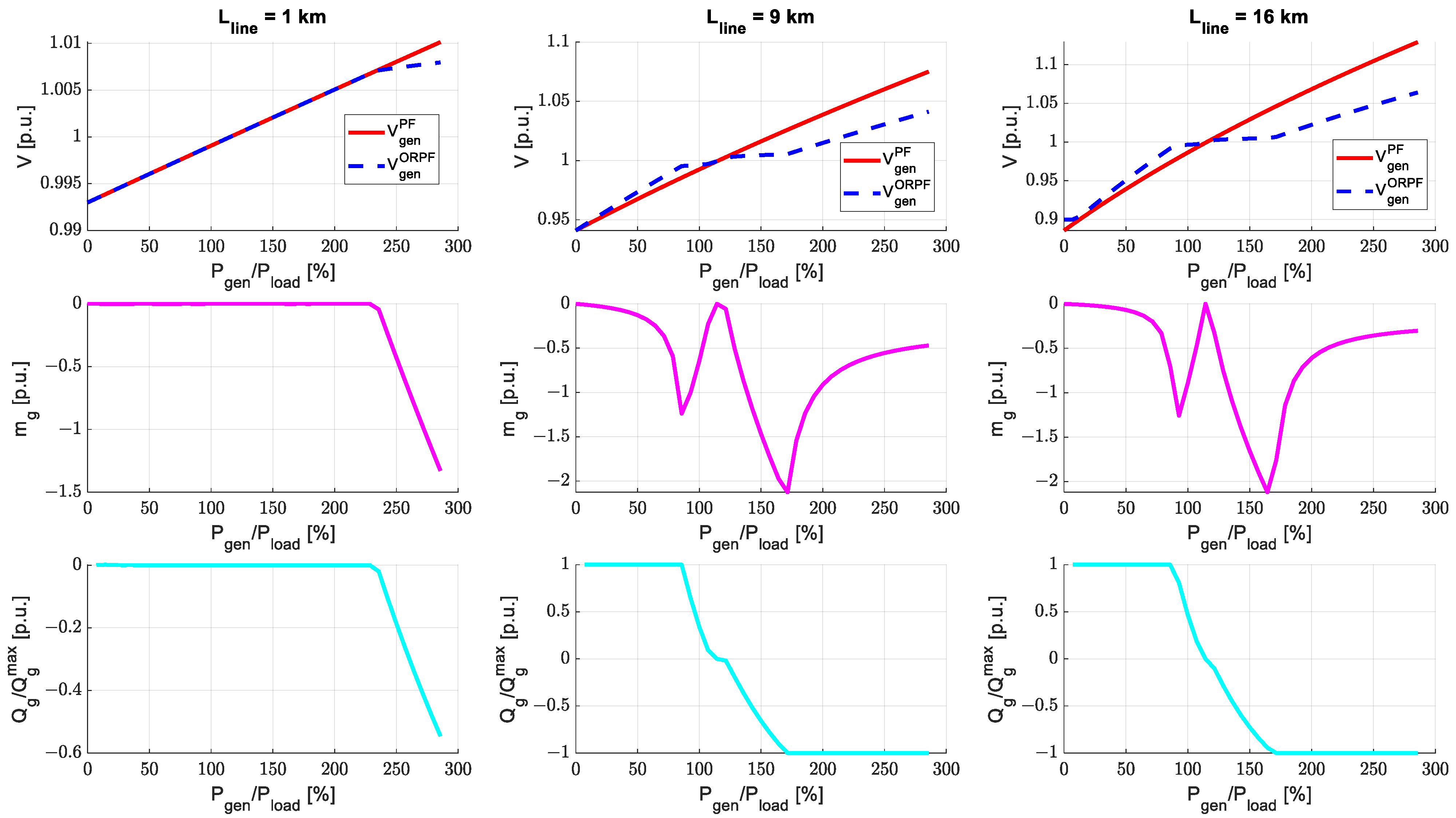
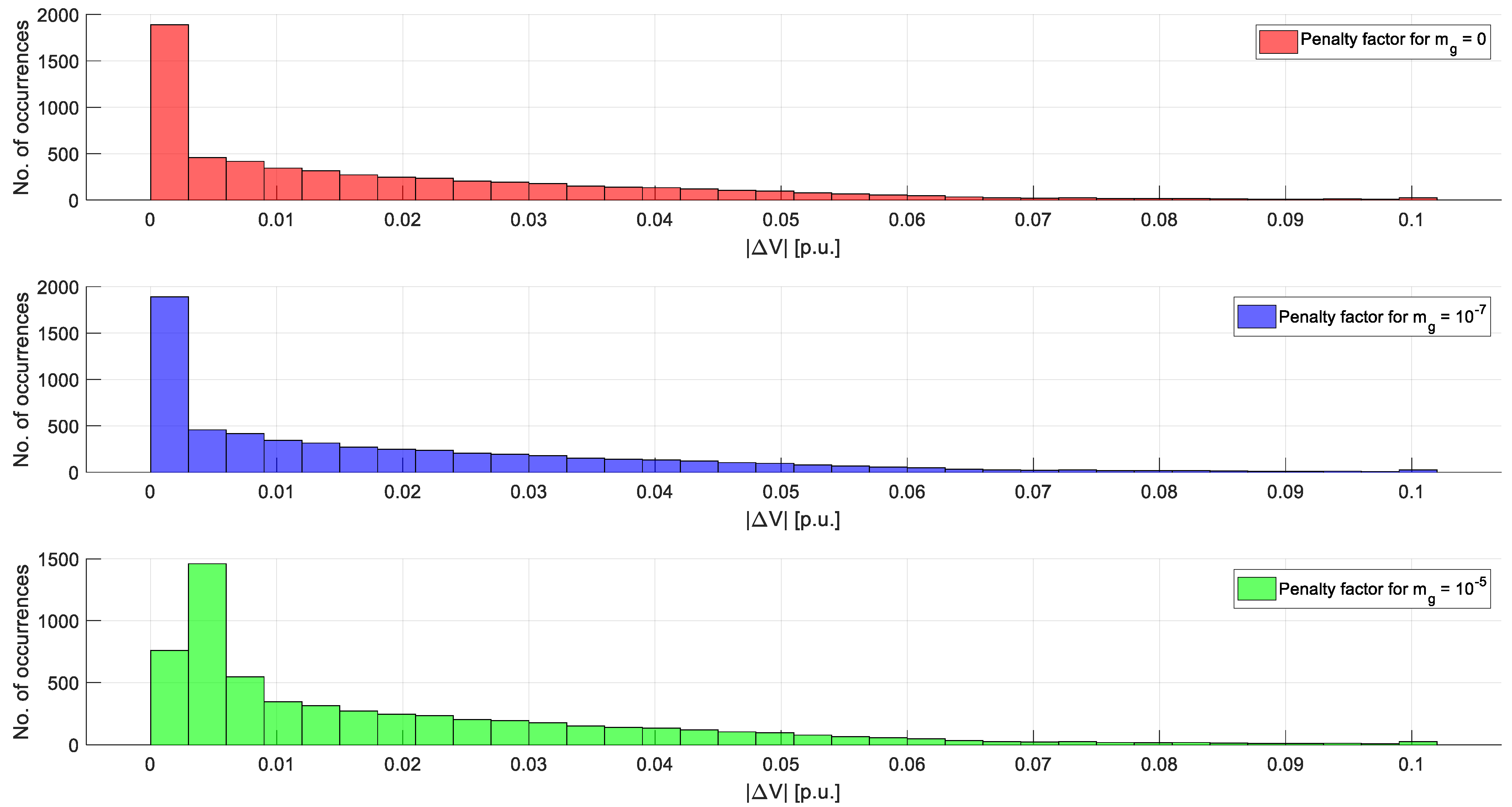
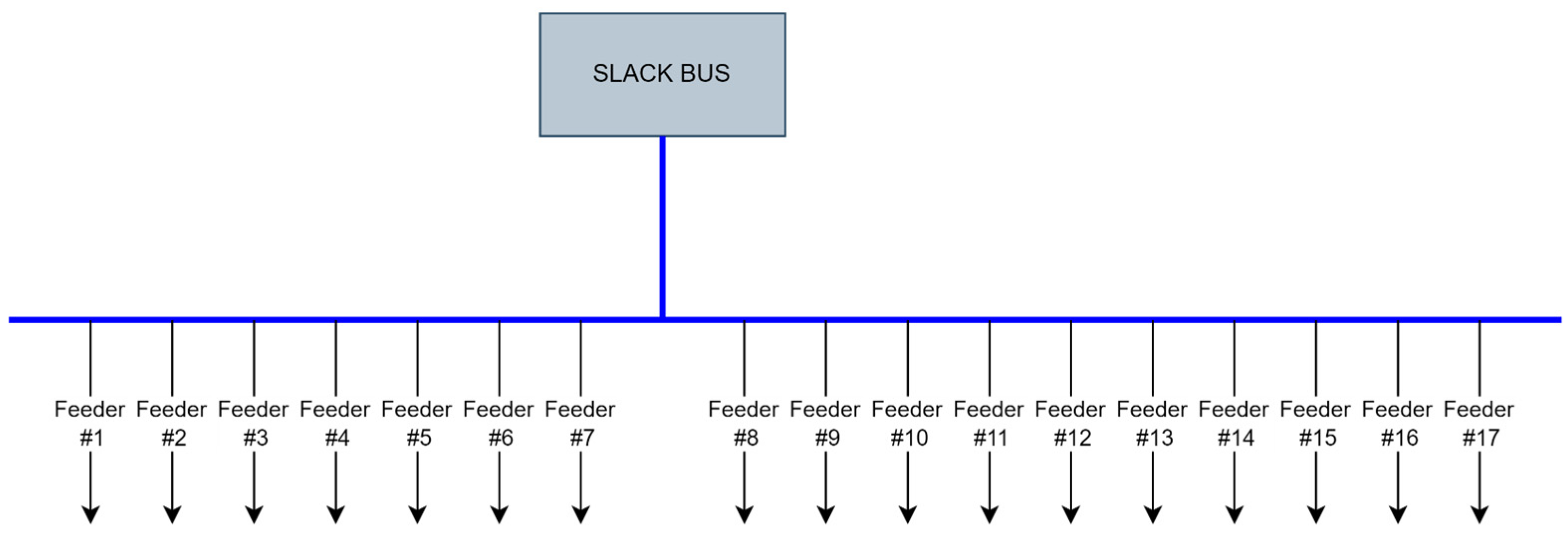
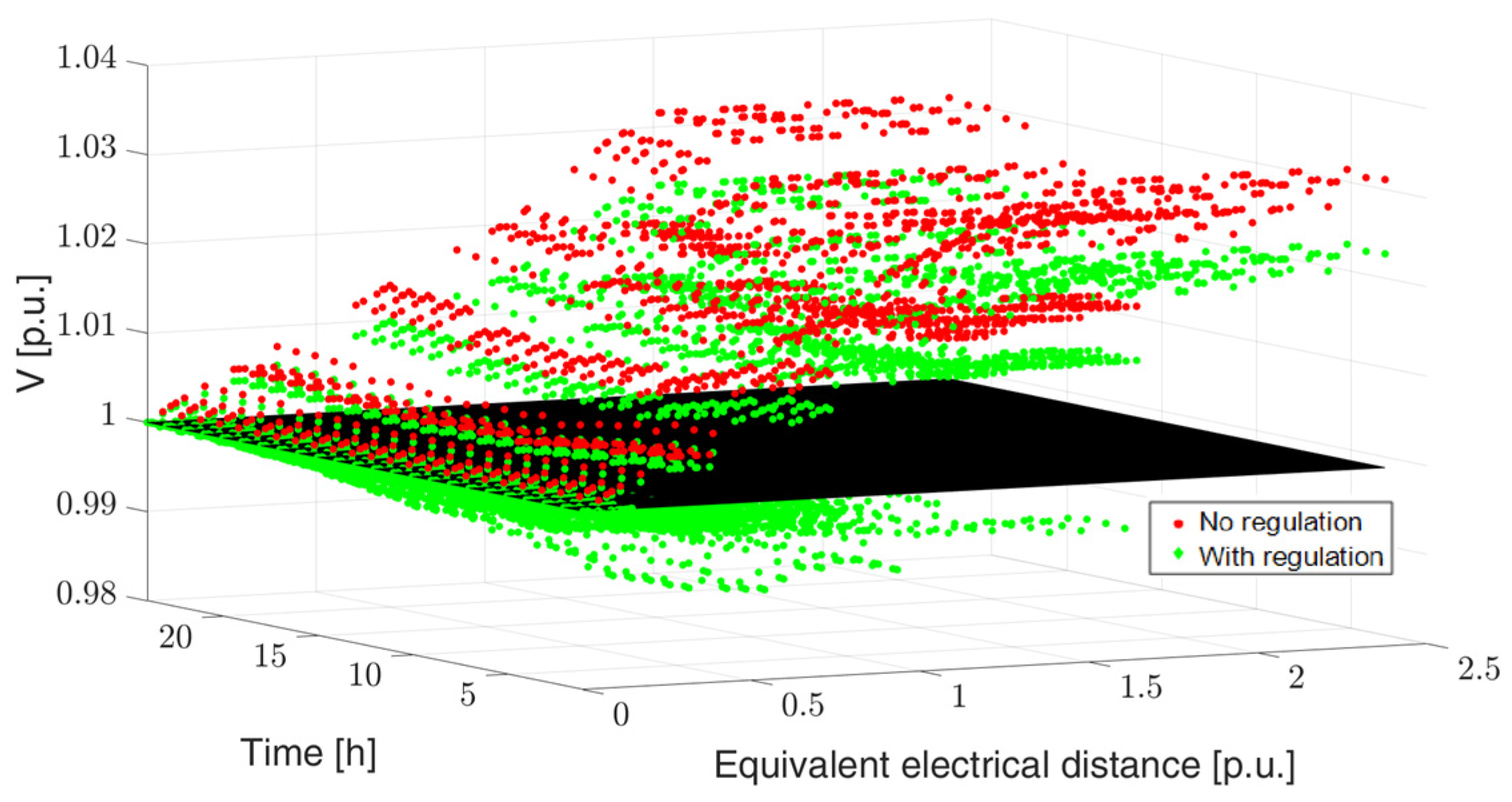
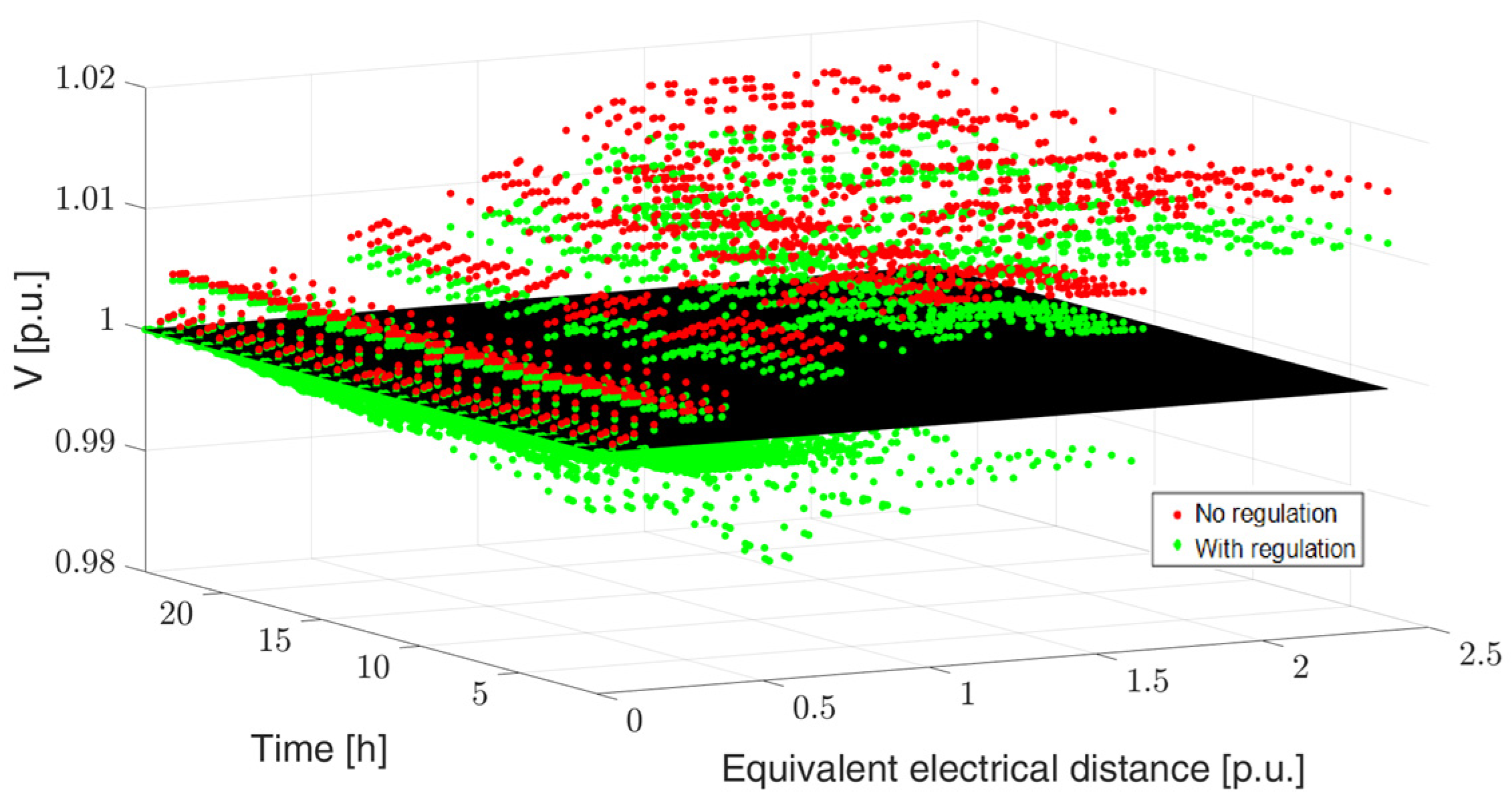
4.1. Test on a Small-Scale Distribution Network
Numerical Results: Minimisation of Voltage Variations
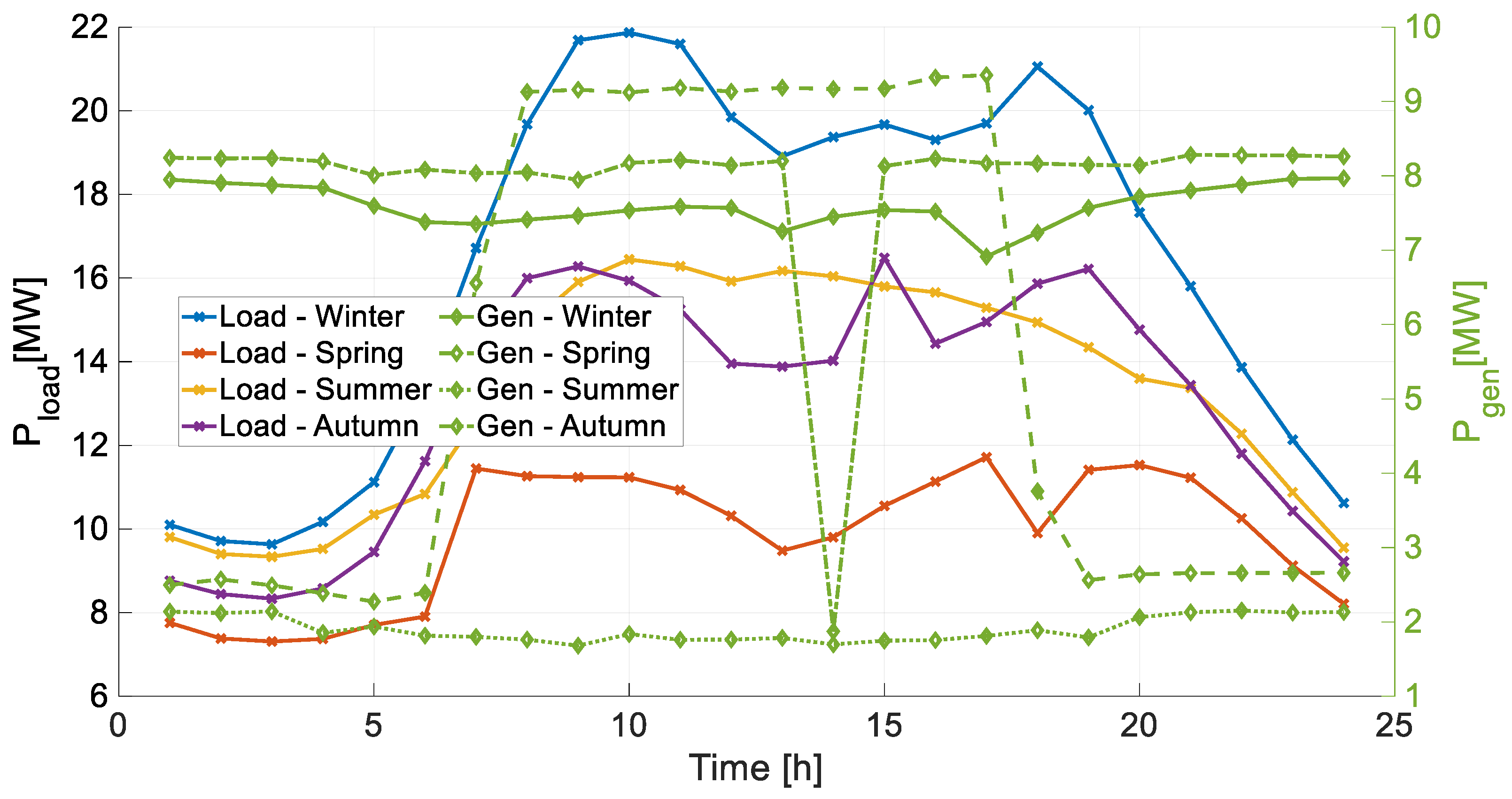
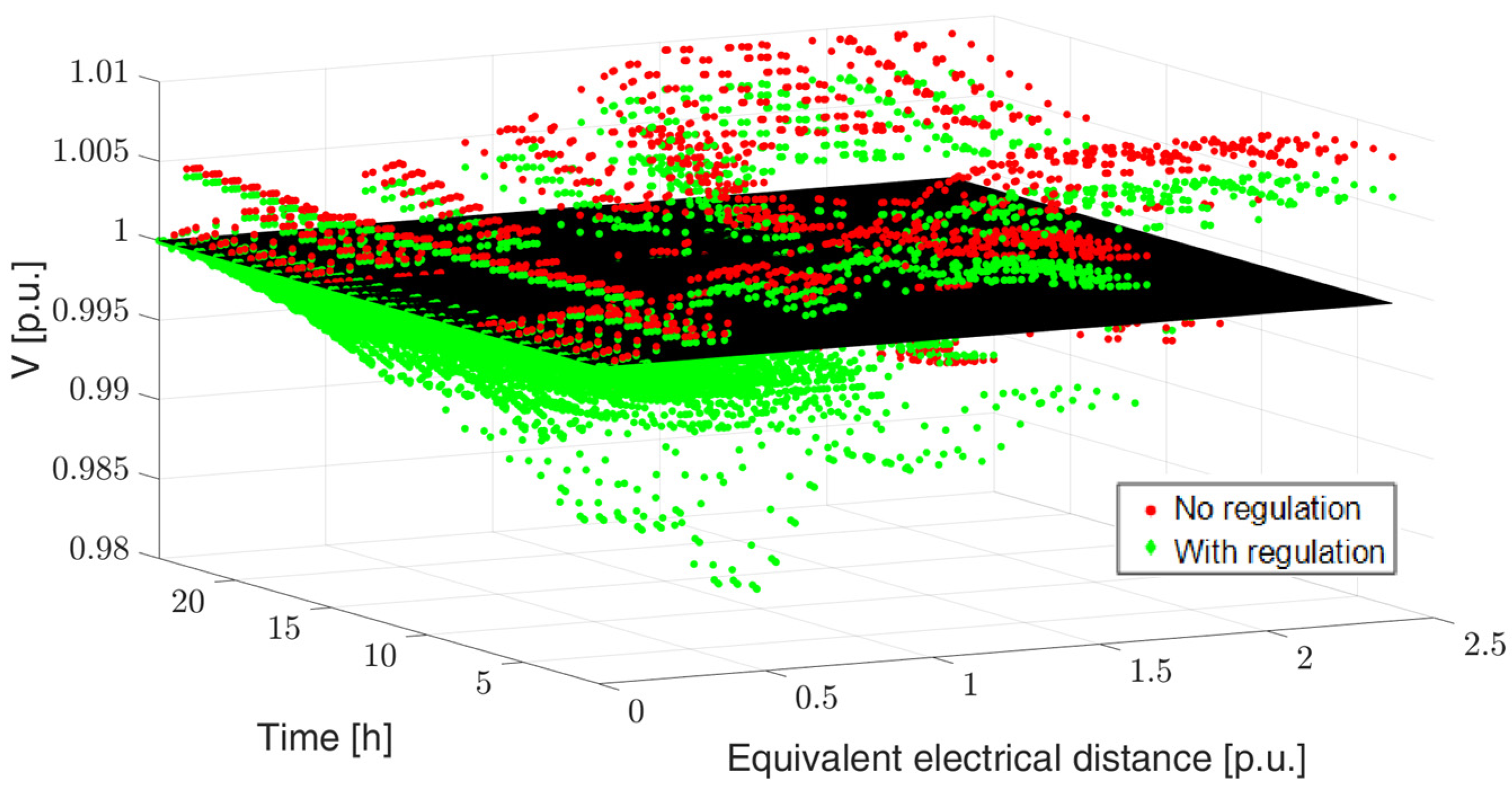
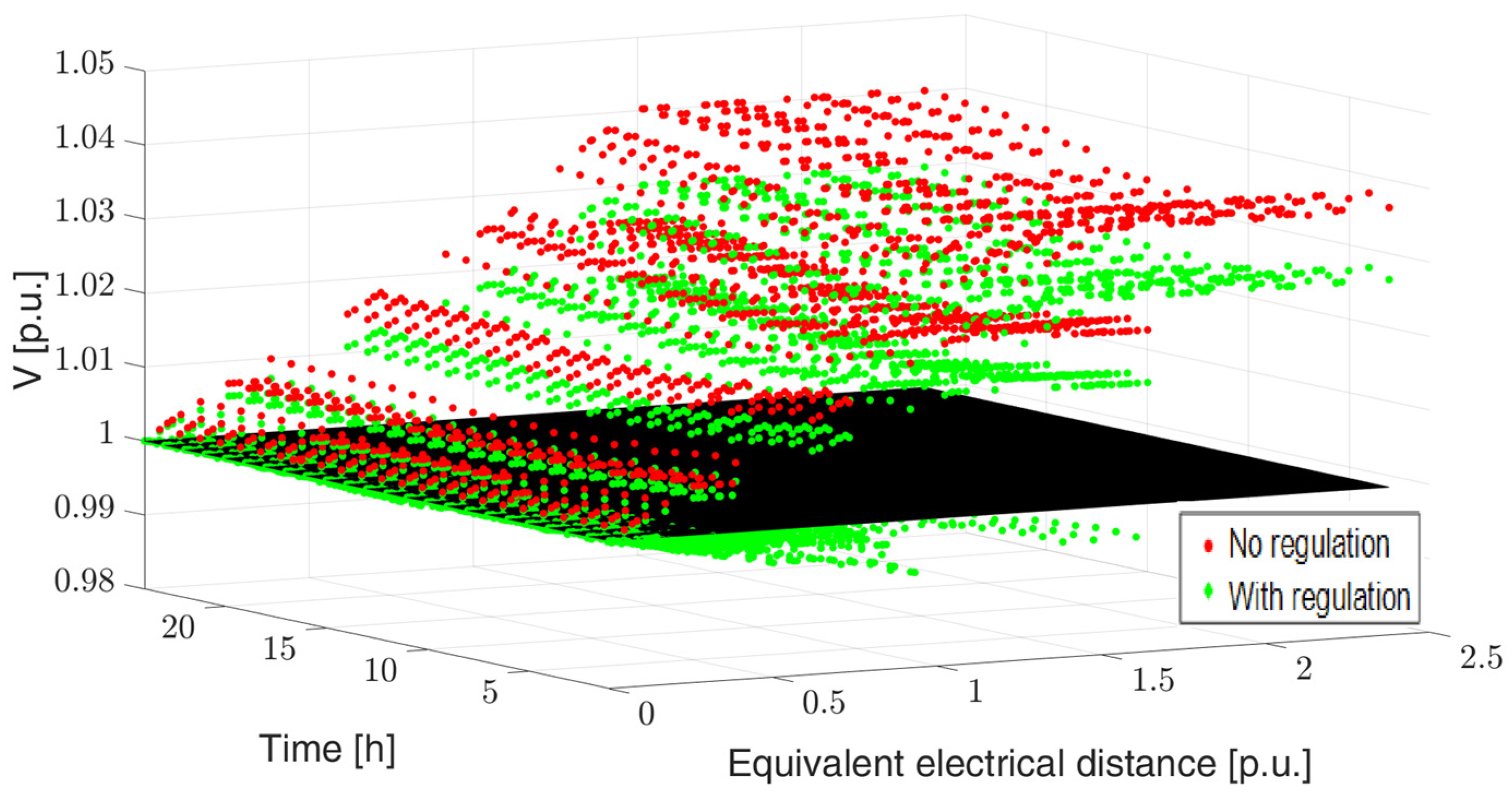
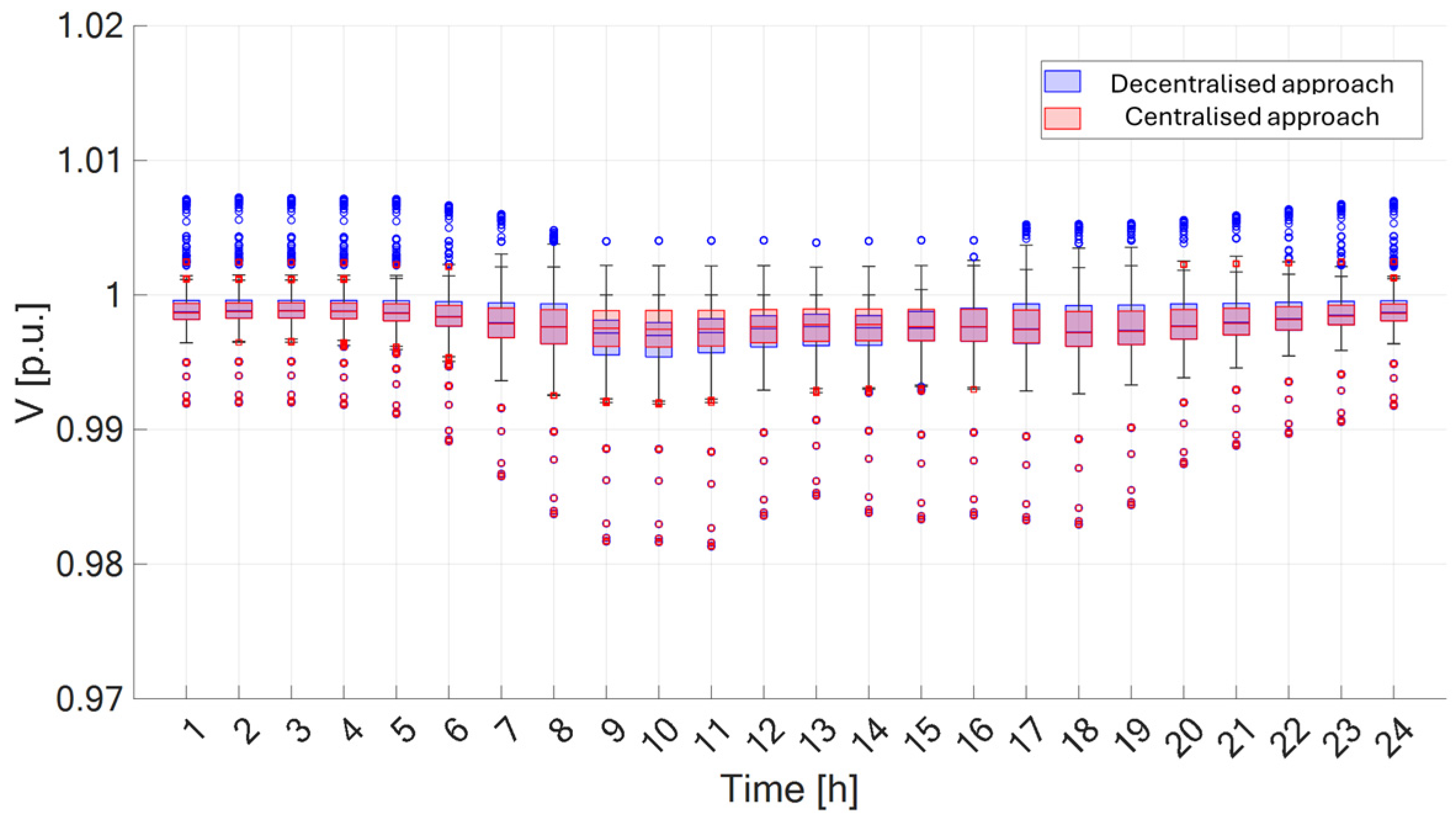
4.2. The Aosta Case Study
- is the hourly power consumption of the i-th secondary substation (SS);
- is the hourly power consumption of the primary substation (PS);
- is the summation of the MV users’ hourly consumption. This parameter also includes the distributed generation;
- is the apparent power of the transformer installed in the j-th secondary substation.
5. Conclusions and Future Studies
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IEA. Renewables 2023. Available online: https://www.iea.org/reports/renewables-2023 (accessed on 27 February 2024).
- Jiang, T.; He, X.; Su, B.; Havea, P.H.; Wei, K.; Kundzewicz, Z.W.; Liu, D. COP28: Challenge of coping with climate crisis. Innovation 2024, 5, 100559. [Google Scholar]
- Smeeth, L.; Haines, A. COP 28: Ambitious climate action is needed to protect health. BMJ 2023, 383, 2938. [Google Scholar] [CrossRef] [PubMed]
- Abbasi, K.; Ali, P.; Barbour, V.; Benfield, T.; Bibbins-Domingo, K.; Hancocks, S.; Horton, R.; Laybourn-Langton, L.; Mash, R.; Sahni, P.; et al. COP28 Climate Change Conference: Time to treat the climate and nature crisis as one indivisible global health emergency. Afr. J. Clin. Exp. Microbiol. 2023, 6, 1–4. [Google Scholar] [CrossRef]
- Bovera, F.; Spiller, M.; Zatti, M.; Rancilio, G.; Merlo, M. Development; validation, and testing of advanced mathematical models for the optimisation of BESS operation. Sustain. Energy Grids Netw. 2023, 36, 101152. [Google Scholar] [CrossRef]
- Shao, S.; Pipattanasomporn, M.; Rahman, S. Challenges of PHEV penetration to the residential distribution network. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–8. [Google Scholar] [CrossRef]
- Ambrosini, G.; Daccò, E.; Falabretti, D.; Gulotta, F.; Premarini, S. Reactive Power Flows on Distribution Networks with Dispersed Generation: Current Trends and Opportunities. In Proceedings of the 2023 AEIT International Annual Conference (AEIT), Rome, Italy, 5–7 October 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Samadi, A.; Shayesteh, E.; Eriksson, R.; Rawn, B.; Söder, L. Multi-Objective Coordinated Droop-Based Voltage Regulation in Distribution Grids with PV Systems. Renew. Energy 2014, 71, 315–323. [Google Scholar] [CrossRef]
- Salih, S.N.; Chen, P. On Coordinated Control of OLTC and Reactive Power Compensation for Voltage Regulation in Distribution Systems with Wind Power. IEEE Trans. Power Syst. 2016, 31, 4026–4035. [Google Scholar] [CrossRef]
- Nour, A.M.M.; Hatata, A.Y.; Helal, A.A.; El-Saadawi, M.M. Review on Voltage-violation Mitigation Techniques of Distribution Networks with Distributed Rooftop PV Systems. IET Gener. Transm. Distrib. 2020, 14, 349–361. [Google Scholar] [CrossRef]
- Bozalakov, D.V.; Laveyne, J.; Desmet, J.; Vandevelde, L. Overvoltage and voltage unbalance mitigation in areas with high penetration of renewable energy resources by using the modified three-phase damping control strategy. Electr. Power Syst. Res. 2019, 168, 283–294. [Google Scholar] [CrossRef]
- Kontis, E.O.; Kryonidis, G.C.; Nousdilis, A.I.; Malamaki, K.N.D.; Papagiannis, G.K. A Two-Layer Control Strategy for Voltage Regulation of Active Unbalanced LV Distribution Networks. Int. J. Electr. Power Energy Syst. 2019, 111, 216–230. [Google Scholar] [CrossRef]
- Etherden, N.; Bollen, M.H.J. Overload and Overvoltage in Low-Voltage and Medium-Voltage Networks Due to Renewable Energy–Some Illustrative Case Studies. Electr. Power Syst. Res. 2014, 114, 39–48. [Google Scholar] [CrossRef]
- Caballero-Peña, J.; Cadena-Zarate, C.; Parrado-Duque, A.; Osma-Pinto, G. Distributed energy resources on distribution networks: A systematic review of modelling, simulation, metrics, and impacts. Int. J. Electr. Power Energy Syst. 2022, 138, 107900. [Google Scholar] [CrossRef]
- Nebuloni, R.; Ilea, V.; Berizzi, A.; Bovo, C.; Arrigoni, C.; Corti, F.; Conte, B.; Bonera, R. Optimal management of flexibility services in LV distribution grids. In Proceedings of the IET Conference Proceedings, Rome, Italy, 12–15 June 2023; pp. 2034–2038. [Google Scholar] [CrossRef]
- European Committee for Electrotechnical Standardization. CENELEC European Standard EN 50160: Voltage Characteristics of Electricity Supplied by Public Electricity Networks; European Committee for Electrotechnical Standardization: Brussels, The Netherlands, 2010. [Google Scholar]
- Singh, R.R.; Bhatti, G.; Saravanan, D. New-age condition monitoring of on-load tap changing transformers in distributed energy systems for Industry 4.0. E-Prime—Adv. Electr. Eng. Electron. Energy 2022, 2, 100087. [Google Scholar] [CrossRef]
- Italian Electrotechnical Committee. CEI 0-16: Reference Technical Rules for the Connection of Active and Passive Consumers to the HV and MV Electrical Networks of Distribution Company. Available online: https://standards.globalspec.com/std/14505610/0-16 (accessed on 27 February 2024).
- Italian Electrotechnical Committee. CEI 0-21: Reference Technical Rules for the Connection of Active and Passive Consumers to the LV Electrical Networks of Distribution Company. Available online: https://standards.globalspec.com/std/14505609/0-21 (accessed on 27 February 2024).
- ENTSO-E. ENTSO-E Network Code for Requirements for Grid Connection Applicable to All Generators. Available online: https://www.entsoe.eu/fileadmin/user_upload/_library/resources/RfG/130308_Final_Version_NC_RfG.pdf (accessed on 27 February 2024).
- Ilea, V.; Bovo, C.; Falabretti, D.; Merlo, M.; Arrigoni, C.; Bonera, R.; Rodolfi, M. Voltage Control Methodologies in Active Distribution Networks. Energies 2020, 13, 3293. [Google Scholar] [CrossRef]
- Guzman-Henao, J.; Grisales-Noreña, L.F.; Restrepo-Cuestas, B.J.; Montoya, O.D. Optimal Integration of Photovoltaic Systems in Distribution Networks from a Technical, Financial, and Environmental Perspective. Energies 2023, 16, 562. [Google Scholar] [CrossRef]
- Mahmud, N.; Zahedi, A. Review of control strategies for voltage regulation of the smart distribution network with high penetration of renewable distributed generation. Renew. Sustain. Energy Rev. 2016, 64, 582–595. [Google Scholar] [CrossRef]
- Wang, Y.; Tan, K.T.; Peng, X.Y.; So, P.L. Coordinated Control of Distributed Energy-Storage Systems for Voltage Regulation in Distribution Networks. IEEE Trans. Power Deliv. 2016, 31, 1132–1141. [Google Scholar] [CrossRef]
- Masters, C.L. Voltage rise: The big issue when connecting embedded generation to long 11 kV overhead lines. Power Eng. J. 2002, 16, 5–12. [Google Scholar] [CrossRef]
- Elkhatib, M.E.; El Shatshat, R.; Salama, M.M.A. Optimal Control of Voltage Regulators for Multiple Feeders. IEEE Trans. Power Deliv. 2009, 25, 2670–2675. [Google Scholar] [CrossRef]
- Todorovski, M. Transformer Voltage Regulation—Compact Expression Dependent on Tap Position and Primary/Secondary Voltage. IEEE Trans. Power Deliv. 2014, 29, 1516–1517. [Google Scholar] [CrossRef]
- Bajaj, M.; Singh, A.K. Grid integrated renewable DER systems: A review of power quality challenges and state-of-the-art mitigation techniques. Int. J. Energy Res. 2020, 44, 26–69. Available online: https://onlinelibrary.wiley.com/doi/pdf/10.1002/er.4847 (accessed on 27 February 2024). [CrossRef]
- Han, X.; Kosek, A.M.; Bondy DE, M.; Bindner, H.W.; You, S.; Tackie, D.V.; Mehmedalic, J.; Thordarson, F. Assessment of distribution grid voltage control strategies in view of deployment. In Proceedings of the 2014 2nd IEEE International Workshop on Intelligent Energy Systems, San Diego, CA, USA, 8 October 2014; IEEE: Piscataway, NJ, USA. [Google Scholar]
- Srivastava, P.; Haider, R.; Nair, V.J.; Venkataramanan, V.; Annaswamy, A.M.; Srivastava, A.K. Voltage regulation in distribution grids: A survey. Annu. Rev. Control. 2023, 55, 165–181. [Google Scholar] [CrossRef]
- Gulotta, F.; Daccò, E.; Bosisio, A.; Falabretti, D. Opening of Ancillary Service Markets to Distributed Energy Resources: A Review. Energies 2023, 16, 2814. [Google Scholar] [CrossRef]
- Li, H.; Liu, W.; Yu, L. Centralized-local PV voltage control considering opportunity constraint of short-term fluctuation. Glob. Energy Interconnect. 2023, 6, 81–91. [Google Scholar] [CrossRef]
- Hatata, A.Y.; Hasan, E.O.; Alghassab, M.A.; Sedhom, B.E. Centralized Control Method for Voltage Coordination Challenges With OLTC and D-STATCOM in Smart Distribution Networks Based IoT Communication Protocol. IEEE Access 2023, 11, 11903–11922. [Google Scholar] [CrossRef]
- Bouhafs, F.; Mackay, M.; Merabti, M. Links to the Future: Communication Requirements and Challenges in the Smart Grid. IEEE Power Energy Mag. 2012, 10, 24–32. [Google Scholar] [CrossRef]
- Dragičević, T.; Lu, X.; Vasquez, J.C.; Guerrero, J.M. DC Microgrids—Part I: A Review of Control Strategies and Stabilization Techniques. IEEE Trans. Power Electron. 2016, 31, 4876–4891. [Google Scholar] [CrossRef]
- Lo, C.-H.; Ansari, N. Decentralised Controls and Communications for Autonomous Distribution Networks in Smart Grid. IEEE Trans. Smart Grid 2013, 4, 66–77. [Google Scholar] [CrossRef]
- Yorino, N.; Zoka, Y.; Watanabe, M.; Kurushima, T. An Optimal Autonomous Decentralized Control Method for Voltage Control Devices by Using a Multi-Agent System. IEEE Trans. Power Syst. 2015, 30, 2225–2233. [Google Scholar] [CrossRef]
- Hu, D.; Li, Z.; Ye, Z.; Peng, Y.; Xi, W.; Cai, T. Multi-agent graph reinforcement learning for decentralised Volt-VAR control in power distribution systems. Int. J. Electr. Power Energy Syst. 2024, 155 Pt A, 109531. [Google Scholar] [CrossRef]
- Zhang, B.; Cao, D.; Hu, W.; Ghias, A.M.Y.M.; Chen, Z. Physics-Informed Multi-Agent deep reinforcement learning enabled distributed voltage control for active distribution network using PV inverters. Int. J. Electr. Power Energy Syst. 2024, 155 Pt B, 109641. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, Z.; Sun, Q.; Gu, W.; Zheng, S.; Zhao, J. Application and progress of artificial intelligence technology in the field of distribution network voltage Control: A review. Renew. Sustain. Energy Rev. 2024, 192, 114282. [Google Scholar] [CrossRef]
- Fusco, G.; Russo, M.; De Santis, M. Decentralized Voltage Control in Active Distribution Systems: Features and Open Issues. Energies 2021, 14, 2563. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghavidel, S.; Akbari, E.; Vahed, A.A. Solving non-linear, non-smooth and non-convex optimal power flow problems using chaotic invasive weed optimisation algorithms based on chaos. Energy 2014, 73, 340–353. [Google Scholar] [CrossRef]
- Ahmadian, A.; Sedghi, M.; Aliakbar-Golkar, M.; Elkamel, A.; Fowler, M. Optimal probabilistic based storage planning in tap-changer equipped distribution network including PEVs, capacitor banks and WDERs: A case study for Iran. Energy 2016, 112, 984–997. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, J.; Liu, R.; Shan, Y. A P-Q Coordination Control Strategy of VSC-HVDC and BESS for LVRT Recovery Performance Enhancement. Electronics 2024, 13, 741. [Google Scholar] [CrossRef]
- Naderi, E.; Narimani, H.; Pourakbari-Kasmaei, M.; Cerna, F.V.; Marzband, M.; Lehtonen, M. State-of-the-Art of Optimal Active and Reactive Power Flow: A Comprehensive Review from Various Standpoints. Processes 2021, 9, 1319. [Google Scholar] [CrossRef]
- Alsac, O.; Bright, J.; Prais, M.; Stott, B. Further developments in LP-based optimal power flow. IEEE Trans. Power Syst. 1990, 5, 697–711. [Google Scholar] [CrossRef]
- Giraldo, J.S.; Vergara, P.P.; López, J.C.; Nguyen, P.H.; Paterakis, N.G. A Linear AC-OPF Formulation for Unbalanced Distribution Networks. IEEE Trans. Ind. Appl. 2021, 57, 4462–4472. [Google Scholar] [CrossRef]
- Bovo, C.; Ilea, V.; Subasic, M.; Zanellini, F.; Arrigoni, C.; Bonera, R. Improvement of observability in poorly measured distribution networks. In Proceedings of the 2014 Power Systems Computation Conference, Wroclaw, Poland, 18–22 August 2014; pp. 1–7. [Google Scholar] [CrossRef]
- Brinkmann, B.; Negnevitsky, M. A Probabilistic Approach to Observability of Distribution Networks. IEEE Trans. Power Syst. 2017, 32, 1169–1178. [Google Scholar] [CrossRef]
- Pokhrel, B.R.; Bak-Jensen, B.; Pillai, R.J. Integrated Approach for Network Observability and State Estimation in Active Distribution Grid. Energies 2019, 12, 2230. [Google Scholar] [CrossRef]
- Montanari, A.N.; Aguirre, L.A. Observability of Network Systems: A Critical Review of Recent Results. J. Control. Autom. Electr. Syst. 2020, 31, 1348–1374. [Google Scholar] [CrossRef]
- Nuaekaew, K.; Artrit, P.; Pholdee, N.; Bureerat, S. Optimal reactive power dispatch problem using a two-archive multi-objective grey wolf optimiser. Expert Syst. Appl. 2017, 87, 79–89. [Google Scholar] [CrossRef]
- Prysmian Group. Low and Medium Voltage Cables and Accessories Catalogue. Available online: https://na.prysmian.com/markets/electrification/industrial-and-construction/building-wire/accessories/low-and-medium-accessories (accessed on 27 February 2024).
- GAMS Development Corporation. General Algebraic Modeling System (GAMS) Release 38.3.0; GAMS Development Corporation: Fairfax, VA, USA, 2022. [Google Scholar]
- Byrd, R.H.; Nocedal, J.; Waltz, R.A. KNITRO: An integrated package for non-linear optimisation. In Large-Scale Non-linear Optimization; di Pillo, G., Roma, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 35–59. [Google Scholar]
- Mirbagheri, S.M.; Merlo, M. Optimal reactive power flow procedure to set up an effective local voltage control. Sustain. Energy Technol. Assess. 2020, 39, 100709. [Google Scholar] [CrossRef]
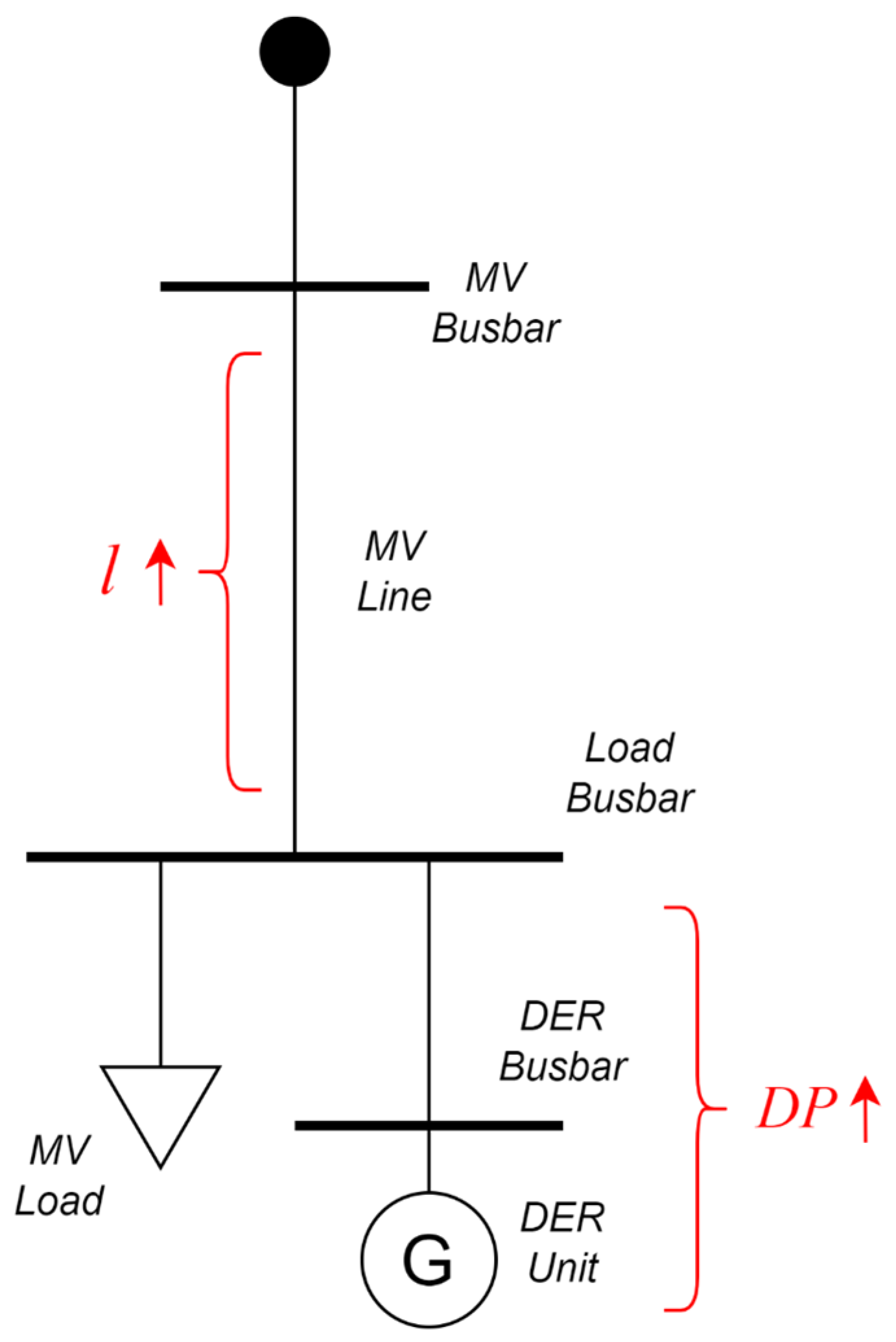
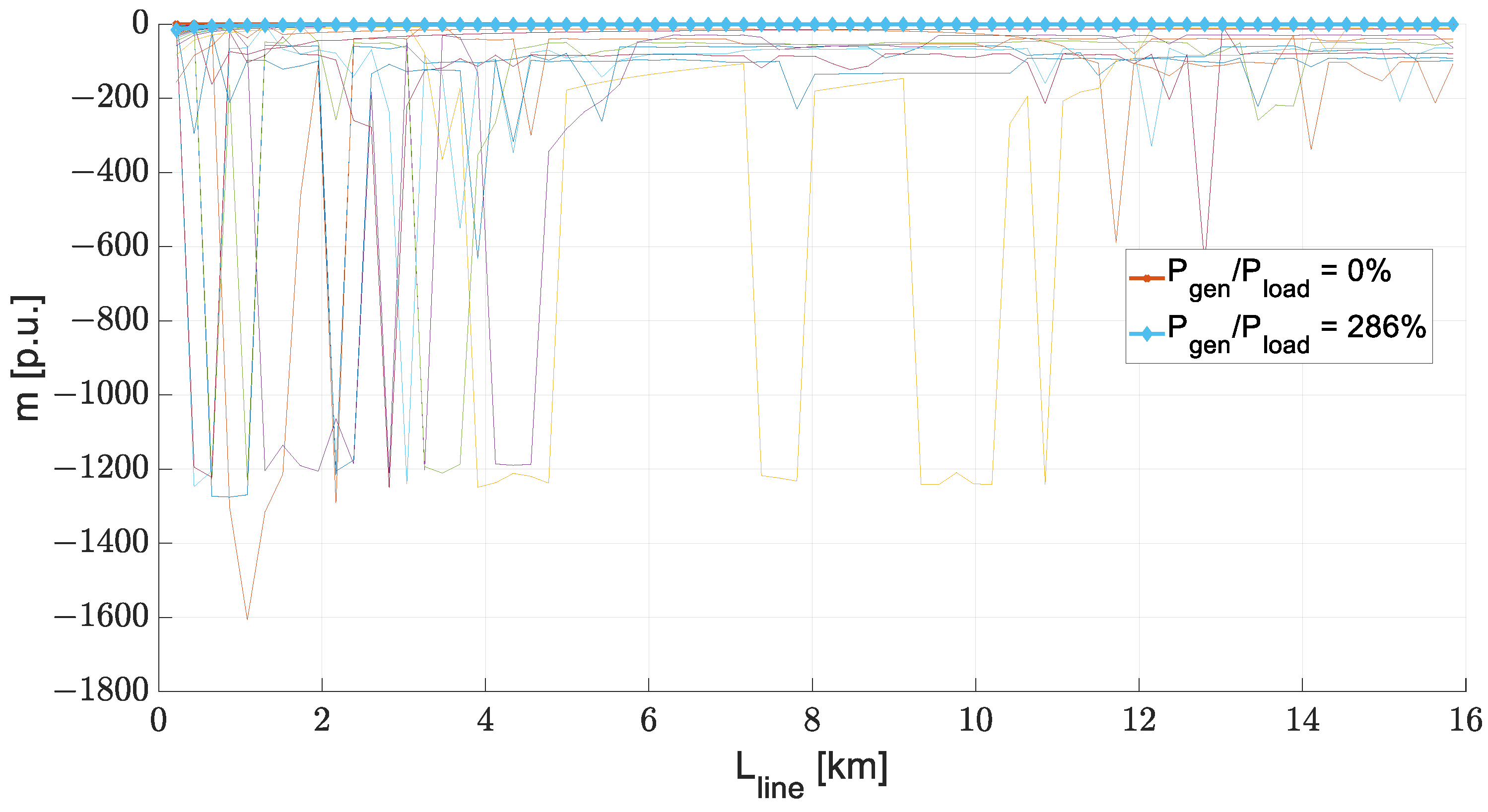
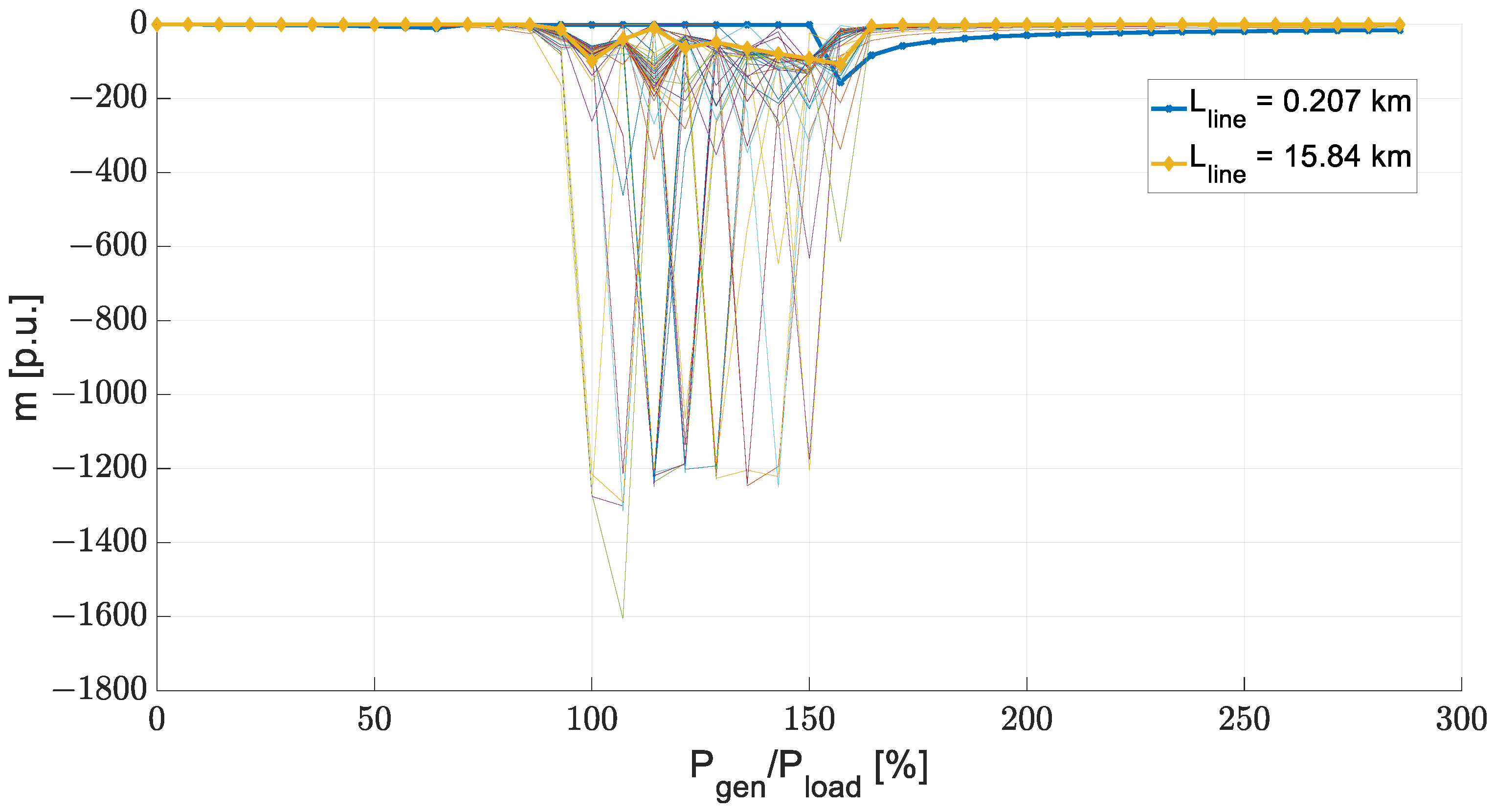

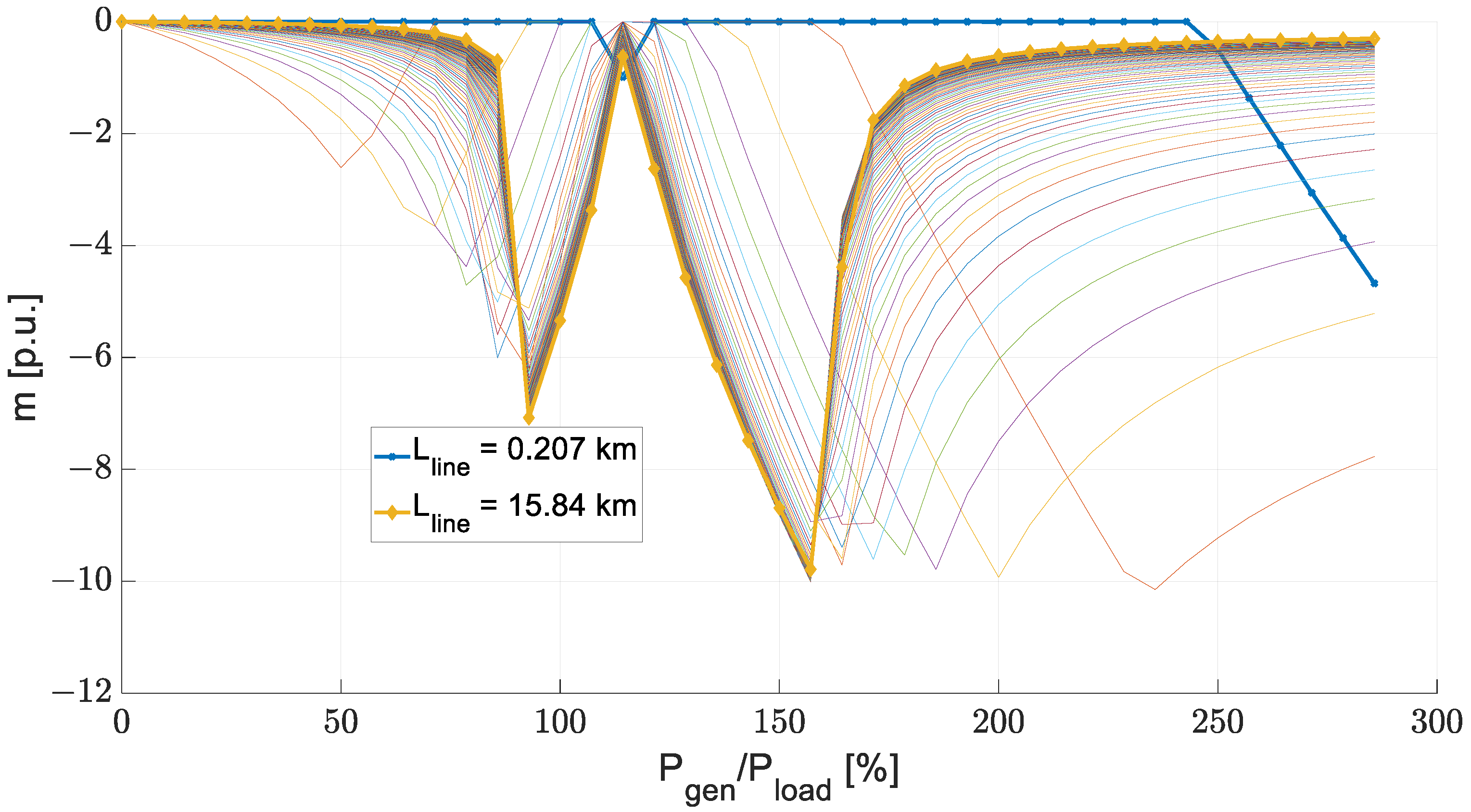
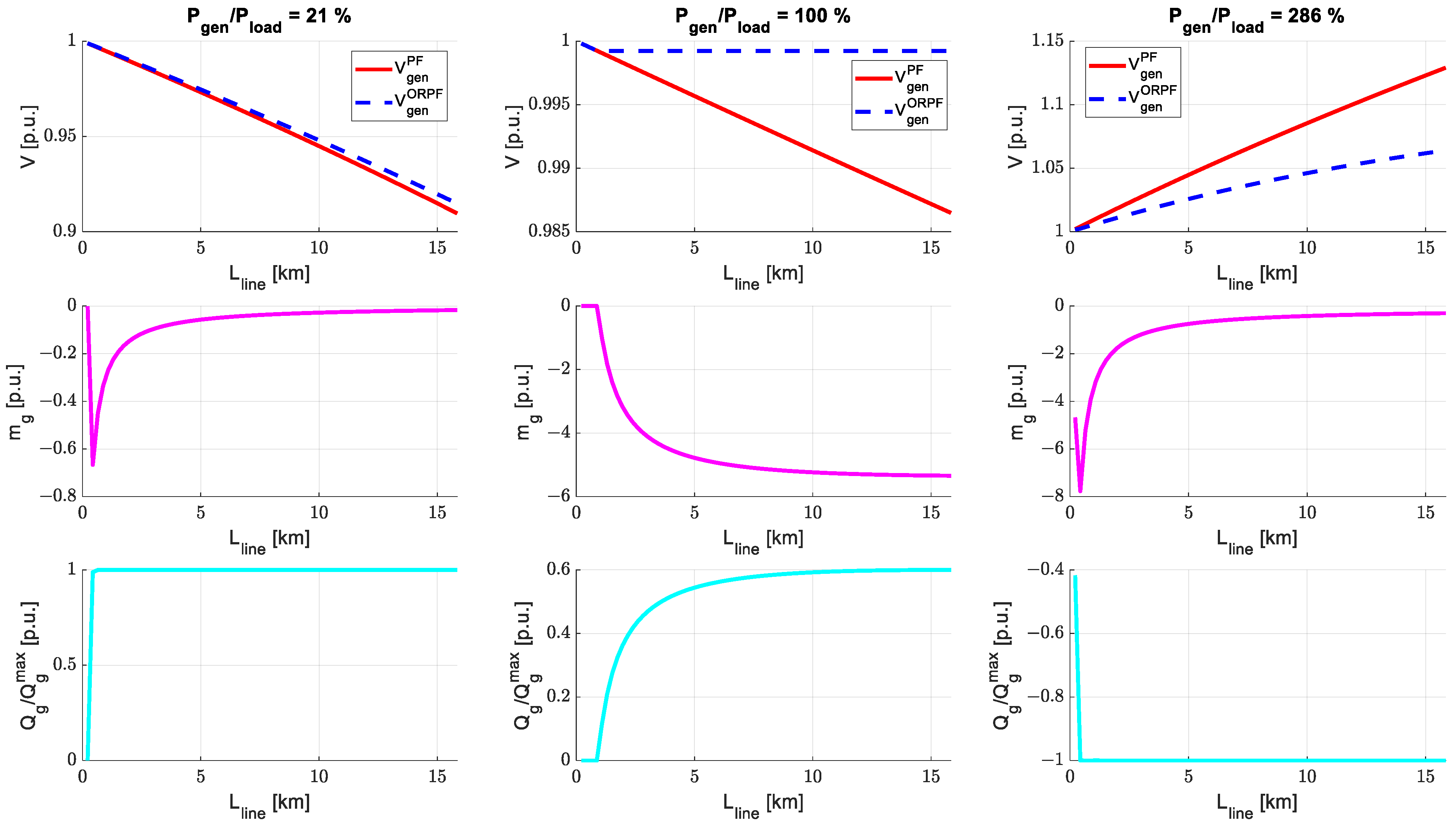
| Production/Load Active Power Ratio DP | Line Length l |
|---|---|
| , generator growth index , line-length growth index | |
| Day | Consumption [MWh] | DG Production [MWh] | Reference Figure |
|---|---|---|---|
| 7 February | 562.755 | 191.890 | Figure 16 |
| 25 May | 355.964 | 132.565 | Figure 17 |
| 2 August | 407.274 | 44.732 | Figure 18 |
| 17 October | 472.981 | 196.267 | Figure 19 |
| Voltages Root Mean Square Error | |||
|---|---|---|---|
| Without Regulation | With Regulation | ||
| Season | Winter | 0.0036 | 0.0034 |
| Spring | 0.0113 | 0.0084 | |
| Summer | 0.0087 | 0.0066 | |
| Autumn | 0.0052 | 0.0041 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daccò, E.; Falabretti, D.; Ilea, V.; Merlo, M.; Nebuloni, R.; Spiller, M. Decentralised Voltage Regulation through Optimal Reactive Power Flow in Distribution Networks with Dispersed Generation. Electricity 2024, 5, 134-153. https://doi.org/10.3390/electricity5010008
Daccò E, Falabretti D, Ilea V, Merlo M, Nebuloni R, Spiller M. Decentralised Voltage Regulation through Optimal Reactive Power Flow in Distribution Networks with Dispersed Generation. Electricity. 2024; 5(1):134-153. https://doi.org/10.3390/electricity5010008
Chicago/Turabian StyleDaccò, Edoardo, Davide Falabretti, Valentin Ilea, Marco Merlo, Riccardo Nebuloni, and Matteo Spiller. 2024. "Decentralised Voltage Regulation through Optimal Reactive Power Flow in Distribution Networks with Dispersed Generation" Electricity 5, no. 1: 134-153. https://doi.org/10.3390/electricity5010008
APA StyleDaccò, E., Falabretti, D., Ilea, V., Merlo, M., Nebuloni, R., & Spiller, M. (2024). Decentralised Voltage Regulation through Optimal Reactive Power Flow in Distribution Networks with Dispersed Generation. Electricity, 5(1), 134-153. https://doi.org/10.3390/electricity5010008









