Abstract
The pressure-induced phase transformations of rare earth orthophosphates (REPO4s) have become increasingly relevant in ceramic matrix composite (CMC) research; however, understanding of the shear-dependence of these transformations remains limited. This study employs diamond anvil cell experiments with three pressure media (neon, KCl, sample itself/no medium) to systematically assess the effect of shear on the phase transformations of TbPO4. Results show a lowering of the TbPO4 transformation onset pressure (Ponset) as well as an extension of the xenotime–monazite phase coexistence range under non-hydrostatic conditions. The TbPO4 Ponset under no medium (4.4(3) GPa) is the lowest REPO4 Ponset reported to date and represents a ~50% drop from the hydrostatic Ponset. Enthalpic differences likely account for lower Ponset values in TbPO4 compared to DyPO4. Experiments also show scheelite may be the post-monazite phase of TbPO4; this phase is consistent with observed and predicted REPO4 transformation pathways.
1. Introduction
The deformation mechanisms of rare earth orthophosphates (REPO4s) under complex stress states are highly pertinent to several research fields including geoscience and structural ceramics. In shocked xenotime and monazite minerals, REPO4 deformation microstructures can provide insight into the extreme conditions generated during impact events [1,2,3]. In addition, the pressure-induced xenotime–monazite phase transformation of certain REPO4 compositions offers the possibility of enhanced toughness and plasticity in ceramic matrix composites (CMCs) for aerospace components subject to extreme conditions [4,5]. When tested as CMC fiber coatings, transforming compositions have been shown to deflect or arrest cracks and facilitate fiber sliding at lower stresses than non-transforming compositions [5].
Identifying REPO4 compositions that undergo the pressure-induced xenotime–monazite phase transformation requires understanding the compositional phase boundary in the middle of the lanthanide series. In equilibrium at 1 atm (10−4 GPa), compositions with smaller RE3+ ionic radii (RE = Tb-–Lu, Sc, Y) adopt the xenotime (tetragonal, I41/amd) structure while those with larger RE3+ ionic radii (RE = La-Gd) adopt the monazite (monoclinic, P21/n) structure [6]. Under high hydrostatic pressure, xenotime-structured compositions are known to transform into either the monazite structure or the scheelite (tetragonal, I41/a) structure, with the latter being more favorable in xenotime compositions with the smallest RE3+ ionic radii [7]. The three aforementioned crystal structures are illustrated in Figure 1.
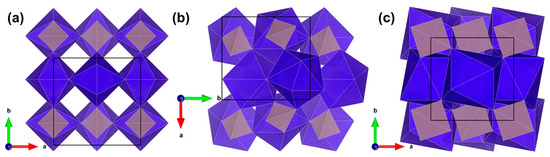
Figure 1.
[001] views of REPO4 structure in the (a) xenotime, (b) monazite, and (c) scheelite phases. RE-O polyhedra are shown in violet, PO4 tetrahedra are shown in grey, and the unit cell boundaries are shown as thin black boxes. The 90° rotation of monazite axes with respect to those of xenotime and scheelite is a result of the monoclinic cell setting of monazite, as shown in the detailed transformation schemes reported by Hay et al. [5]. Figure adapted from Sharma et al. [7].
The xenotime, monazite, and scheelite structures all contain chains of alternating RE-O polyhedra and PO4 tetrahedra and have RE-O coordination numbers of 8, 9, and 8, respectively [8]. Figure 1 shows the compaction of the REPO4 structure from xenotime to monazite to scheelite due to the increasing rotations and translations of the RE-O polyhedra and PO4 tetrahedra [8]. Such rotations and translations can be induced using hydrostatic pressure, and they can be prematurely induced in the presence of non-hydrostatic stress, which disrupts stable bonding symmetries more dramatically than pure hydrostatic stress [5,9]. An intermediate structure, anhydrite (orthorhombic, Amma), has also been reported in xenotime compositions that are extremely close to the xenotime–monazite phase boundary (e.g., Gd0.5Tb0.5PO4) or subjected to high deviatoric stresses at low hydrostatic pressures (e.g., GdxDy1−xPO4, TbPO4) [5,10,11].
While the pressure-induced phase transformations of REPO4s have been extensively characterized in (quasi-)hydrostatic environments via in situ diamond anvil cell (DAC) X-ray diffraction (XRD) and Raman spectroscopy (RS), studies which systematically evaluate the influence of non-hydrostaticity are extremely limited [7]. Such studies typically vary the pressure-transmitting medium (PTM) in the DAC in order to vary the hydrostaticity of the stress state experienced by the sample. For example, Santamaria-Perez et al. studied orthorhombic BaSO4 using three different fluid PTMs (helium, silicone oil, and 4:1 methanol–ethanol), finding a decreasing hydrostatic limit led to lower transformation onset pressures (Ponset) and wider pressure ranges of phase coexistence [12]. In REPO4 literature specifically, Lacomba-Perales et al.’s in situ DAC XRD study notes that shear promotes earlier xenotime–monazite transformation in YPO4, but this conclusion is based on a cursory comparison of their findings to a prior YPO4 study carried out by others [13]. Our recent in situ DAC XRD study probed the effect of shear on the xenotime–monazite transformation of DyPO4 by systematically varying the PTM [9]. We found neon and 16:3:1 methanol–ethanol–water (MEW) PTM yield similar Ponset values of 9.1(1) GPa and 9.3 GPa, respectively, while KCl PTM yields a much lower Ponset of 7.0 GPa (a ~22% drop). Even though neon crystallizes at 4.7 GPa, neon and MEW both remain (quasi-)hydrostatic at Ponset; therefore, employing only one of these two PTMs is sufficient (assuming other conditions are held constant) [14]. The significant Ponset reduction under KCl is likely attributable to a higher shear stress state given the fact that KCl is never hydrostatic, and its ambient pressure bulk modulus (B0) is ~20 times that of neon [15,16,17]. We note that B0 does not reflect the DAC conditions at Ponset since a material’s bulk modulus (B) generally increases with pressure. However, materials whose B0 values differ by orders of magnitude do not attain similar B values at the high pressures of interest. At a given DAC pressure, an increase in the B value of a PTM results in less PTM compression, which is expected to generate greater contact stresses and friction at PTM–sample interfaces. Given the non-uniform magnitude and direction of the contact stresses and friction, greater shear stress is expected to be induced in the sample. While the quantification of stress transfer and shear stress generation by solid PTMs has not been detailed in the literature, results from prior DAC experiments on α-Ti support the expectation that solid PTMs with higher B0 impart more shear stress on the sample than PTMs with lower B0 [18]. Because DyPO4 was not tested under any solid PTM (solid at 1 atm) other than KCl, another high-shear state was not evaluated. Beyond our DyPO4 study, the effect of shear on phase transformations has yet to be reported for any other REPO4 [9]. In addition, the high-pressure, post-monazite phase of TbPO4 has yet to be experimentally observed.
This study employs in situ DAC synchrotron XRD to probe the pressure-induced phase transformations of xenotime TbPO4 under variable hydrostaticity. The experiments performed in this study involve three PTMs: neon, KCl, and “none” (i.e., cell packed with sample and no PTM material). In the “none” PTM condition, the sample is effectively the PTM. Xenotime DyPO4 is also tested in the “none” condition to build on our prior study [9]. DyPO4 and TbPO4 have B0 values of 144 GPa and 134 GPa, respectively, which are an order of magnitude higher than the B0 of KCl [9,19]. Our TbPO4 experiment using neon PTM shows a xenotime–monazite Ponset of 8.7(6) GPa, which is lower than other reported XRD-based hydrostatic Ponset values of 9.8 GPa and 9.9 GPa [19]. In addition, TbPO4 experiments in this study show a systematic lowering of the xenotime–monazite Ponset when changing the PTM from neon to KCl to “none” (i.e., as PTM bulk modulus increases). Lastly, our TbPO4 experiment with no medium shows an almost 50% drop in Ponset (reaching the lowest value reported for any REPO4 to date), provides evidence for scheelite as the post-monazite phase, and corroborates Hay et al.’s ex situ observation of monazite in indented xenotime TbPO4.
2. Materials and Methods
Xenotime TbPO4 and DyPO4 powders were synthesized via precipitation reactions and subsequent calcination. Details of these synthesis steps are provided in the Supplementary Materials. The sample powder consisted of grains ranging from sub-micrometer to a few micrometers in size; these grains exhibited the anisotropic, elongated crystal habit expected of tetragonal materials (see Figure S1). In situ DAC XRD was conducted at room temperature at Beamline 12.2.2 of the Advanced Light Source at Berkeley National Laboratory. For experiments involving neon PTM, DACs were loaded with neon using the University of Chicago Gas Loader in the high-pressure lab at Beamline 12.2.2. Two-dimensional diffraction patterns were collected with a PILATUS 3S 1M detector at an X-ray wavelength of 0.4947 Å and an exposure time of 20 s. All DACs used were of the symmetric Princeton design and were compressed using a membrane driven by a Druck PACE 6000 pressure controller. Additional experiment details are shown in Table 1. In the table and elsewhere in the manuscript, values within parentheses following a pressure represent the standard deviation of the last digit of the pressure.

Table 1.
Details of the XRD experiments performed at Beamline 12.2.2 at the Advanced Light Source.
For pressure marking during initial membrane engagement, ruby was used (R1 fluorescence calibration) [20], while gold was used during diffraction data collection (using a 3rd order Birch–Murnaghan equation of state) [21]. Data collection began at pressures higher than 0 GPa due to some initial compression required to confirm membrane engagement. There are no reported TbPO4 or DyPO4 phase transitions below these starting pressures (as corroborated by prior work); therefore, the initial jump does not preclude any material insight [7,9,19]. The maximum pressure in each experiment (Pmax) was limited by the performance of the gasket. Experiments were concluded when the gasket hole collapsed, approached the edge of the culets, or was otherwise unable to maintain a proper seal.
XRD pattern integration, masking, and background subtraction were performed using Dioptas [22]. Pattern fitting was then performed using X’Pert HighScore Plus 3.0 [23]. This software fits monazite using the P21/c cell setting as a default. Though both the P21/c and P21/n cell settings are valid descriptions of monazite (space group No. 14), fitted lattice parameters were converted to the P21/n cell setting to facilitate comparison to the literature. The LeBail fitting approach was used instead of traditional Rietveld structural refinement to accommodate the significant preferred orientation present in all scans [24]. This apparent preferred orientation appears due to the small spot size of the beam with respect to the grain size of the sample (effectively sampling a finite number of grains), rather than any systematic preferred orientation of the sample grains. Ponset is determined by visual inspection of individual XRD patterns and fit residuals, not by judging color in the contour plots shown in the next section. Visual inspection involves plotting the square root of intensity against Q to ensure emerging peaks are not overlooked due to their extremely low intensity. The following reference structures were used in this study: xenotime TbPO4 from Lopez-Solano et al. [19], xenotime DyPO4 from Milligan et al. [25], monazite TbPO4 and DyPO4 from Heuser et al. [26], anhydrite TbPO4 from Losch et al. [27], gold from Couderc et al. [28], ruby from Jephcoat et al. [29], and calculated scheelite TbPO4 from López-Solano et al. [19]. In the XRD patterns, the peaks of the ruby, anhydrite TbPO4, and scheelite TbPO4 structures are extremely weak or obscured by stronger peaks; as a result, LeBail fits incorporating these phases did not converge. Thus, the peaks of these three phases were only used in peak position comparison and were not employed in LeBail fitting. Traces of the anhydrite phase of TbPO4 appear at the beginning of the Tb-neon experiment and may have arisen inadvertently from grinding during sample preparation or DAC loading. This phase does not appear in every scan (or even in every experiment), as the particular set of sample grains under X-ray illumination varies. For computation involving derived data (e.g., unit cell volume, gold-based pressure, cell setting conversion), the uncertainties Python package was used to propagate error [30].
3. Results and Discussion
Across all experiments, increasing pressure causes XRD peaks to drift to higher Q and broaden due to uniform and non-uniform strain, respectively. In addition, XRD signal quality deteriorates under increasingly non-hydrostatic PTMs (i.e., going from neon to KCl to none); this trend has been previously reported in hydrostaticity studies of other materials [12,18]. Given these effects, the XRD patterns analyzed in the current study are limited to pressures at which key peaks are sufficiently distinguishable for phase identification and LeBail fitting.
For the Tb-neon experiment, Figure 2a shows XRD pattern evolution throughout the entire experiment, while Figure 2b shows LeBail fit quality at Pinitial (1.6(1) GPa), Ponset (8.7(6) GPa), the transformation end pressure (Pend, 13.7(10) GPa), and Pmax (14.0(10) GPa). The first scan in this experiment features xenotime, anhydrite, and gold (upward triangle symbol) peaks. At ~5 GPa, the neon PTM crystallizes, and conditions shift from hydrostatic (in liquid neon) to quasi-hydrostatic (in solid neon) [31]. Solid neon adopts an FCC structure and is still extremely compressible with a bulk modulus of ~1 GPa [32]. Neon remains the most compressible material in the DAC, as evidenced by neon peaks shifting much more dramatically with increasing pressure than the other materials’ peaks in Figure 2a. The first discernible monazite peaks emerge at 8.7(6) GPa and are located at Q = 1.58 Å−1, 1.59 Å−1, 1.98 Å−1, 2.13 Å−1, and 2.29 Å−1 (as denoted by stars in Figure 2); these are the (110), (10), (002), (02), and (21) reflections, respectively. Figure 2 also shows these peaks grow with pressure. In the Ponset scan in Figure 2b, the refined monazite lattice parameters are a = 6.175(1) Å, b = 6.699(1) Å, c = 6.483(1) Å, and β = 100.67(1)°. This Ponset value is higher than neon’s crystallization pressure and lower than neon’s hydrostatic limit, meaning the stress state is quasi-hydrostatic at Ponset. With increasing pressure, monazite peaks grow while xenotime peaks diminish. At 13.7(10) GPa, there are no longer any clearly discernible peaks that are attributable to xenotime. Therefore, 13.7(10) GPa is Pend and yields a xenotime–monazite phase coexistence range of 5.0(10) GPa. In the final scan at 14.0(10) GPa, monazite, gold, and neon are the only phases present.
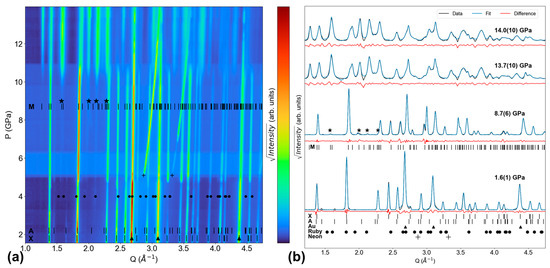
Figure 2.
Tb-neon XRD experiment. (a) Contour plot of all XRD patterns. (b) Select XRD patterns (initial, onset of monazite, end of xenotime, final) and their LeBail fits. Monazite peaks emerge at 8.7(6) GPa. ‘X’, ‘M’, and ‘A’ ticks show TbPO4 peak positions for the xenotime [25], monazite [26], and anhydrite phases [27], respectively. Triangles, circles, pluses, and stars denote the peak positions of gold [28], ruby [29], neon [31], and emerging monazite, respectively.
A key result from the Tb-neon experiment is the Ponset of 8.7(6) GPa, which is the lowest Ponset value for TbPO4 in neon PTM reported to date. Lopez-Solano et al. reported a higher value of 9.9 GPa based on XRD experiments also conducted with neon PTM [19]. Our experiment shows monazite peaks are clear at 9.9 GPa and at pressures leading up to this value (see Figure 2a). Figure 3 provides a closer look at our dataset, showing how including the monazite structure improves the fit of the XRD pattern collected at 8.7(6) GPa.
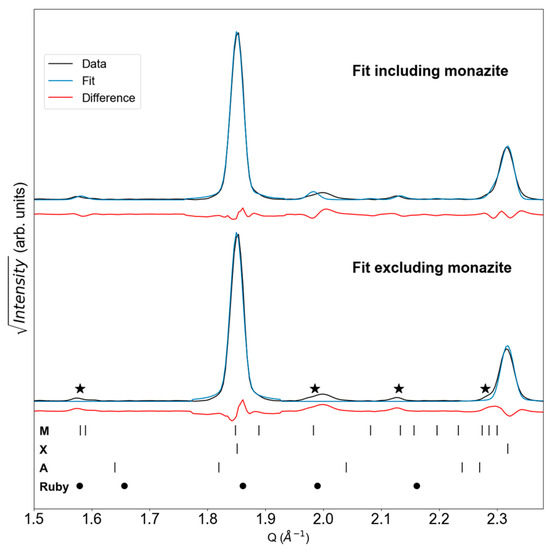
Figure 3.
LeBail fits with and without monazite for the Ponset scan from the Tb-neon experiment. ‘X’, ‘M’, and ‘A’ ticks show TbPO4 peak positions for the xenotime [25], monazite [26], and anhydrite [27] phases, respectively. Circles show reference ruby peak positions [29], and stars indicate regions of intensity consistent with monazite peaks.
When monazite is excluded from the fit, there are regions of increased residual intensity (denoted by stars) that align with monazite peak positions. Although some ruby peaks are also quite close to the starred regions, ruby peaks do not align with all of these regions. Furthermore, the ruby signal is not expected to intensify with pressure, while the intensity in those starred regions does (as shown in Figure 2).
Further consideration of thermodynamic data between neighboring REPO4 compounds gives additional support to a lower Ponset than the one reported by Lopez-Solano et al. [19]. Thermodynamic data (i.e., calculated enthalpy differences between xenotime and monazite phases as well as experimental calcination temperatures required to convert monazite to xenotime) show the monazite phase is more favorable in TbPO4 than in DyPO4 [33,34,35,36]. As a result, TbPO4 is expected to have a lower xenotime–monazite Ponset than DyPO4, but Lopez-Solano et al.’s TbPO4 Ponset is higher than the previously reported DyPO4 Ponset of 9.1(1) GPa (also in neon PTM) [9]. The lower TbPO4 Ponset reported in the present study is consistent with thermodynamic expectations. Nevertheless, the Pend of 13.7(10) GPa determined in this study is consistent with Lopez-Solano et al.’s Pend of 13.8 GPa.
For the Tb-KCl experiment, Figure 4a shows XRD pattern evolution throughout the entire experiment, while Figure 4b shows LeBail fit quality at Pinitial (2.2(2) GPa), Ponset (5.6(4) GPa), and Pmax (11.9(8) GPa). The first scan in this experiment contains peaks belonging to xenotime, gold (upward triangle symbol), and B1-KCl (left-pointing triangle symbol). B1-KCl is the ambient pressure phase of KCl with a NaCl-type structure, and it begins transforming into the CsCl-type B2-KCl structure (right-pointing triangle symbol) at 2.3(1) GPa. Similar to neon in the Tb-neon experiment, KCl in this experiment is the most compressible material in the DAC, causing its peaks to shift in Q more than the sample’s peaks [37]. KCl peaks do not shift as dramatically as neon’s peaks in the Tb-neon experiment because KCl has a higher bulk modulus than neon.
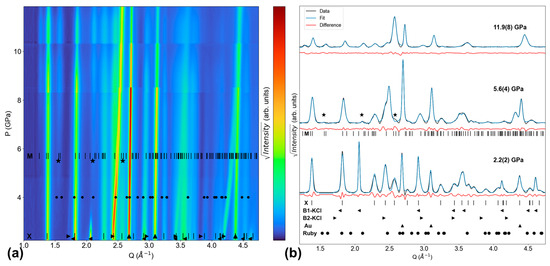
Figure 4.
Tb-KCl XRD experiment. (a) Contour plot of all XRD patterns. (b) Select XRD patterns (initial, onset of monazite, final) and their LeBail fits. Monazite peaks emerge at 5.6(4) GPa. ‘X’ and ‘M’ ticks show TbPO4 peak positions for the xenotime and monazite phases, respectively [25,26]. Circles, upward triangles, left-pointing triangles, right-pointing triangles, and stars denote the peak positions of ruby [29], gold [28], B1-KCl [37], B2-KCl [37], and emerging monazite, respectively.
At 5.6(4) GPa, monazite peaks emerge at Q = 1.55 Å−1, 2.1 Å−1, and 2.58 Å−1 (as denoted by stars in Figure 4); these are the (110), (02), and (211) reflections, respectively. In the Ponset scan, the refined monazite lattice parameters are a = 6.239(1) Å, b = 6.832(3) Å, c = 6.793(1) Å, and β = 99.06(1)°. Both the xenotime and monazite phases persist through the end of the experiment at 11.9(8) GPa, so the phase coexistence range is at least 6.3(8) GPa. In the final scan at 11.9(8) GPa, xenotime, monazite, gold, and B2-KCl are the only phases present.
For the Tb-none experiment, Figure 5a shows XRD pattern evolution throughout the entire experiment, while Figure 5b shows LeBail fit quality at Pinitial (1.9(1) GPa), the xenotime–monazite Ponset (4.4(3) GPa), the potential scheelite Ponset (10.2(7) GPa), and Pmax (19.3(14) GPa). The first scan in this experiment shows xenotime, gold (upward triangle symbol), and possibly weak ruby (circle symbol) peaks. At 4.4(3) GPa, monazite peaks emerge at Q = 1.55 Å−1, 2.10 Å−1, and 2.58 Å−1 (as denoted by stars in Figure 5); these are the (110), (02), and (211) reflections, respectively. In the Ponset scan, the refined monazite lattice parameters are a = 6.134(1) Å, b = 6.870(1) Å, c = 6.187(2) Å, and β = 99.83(2)°.
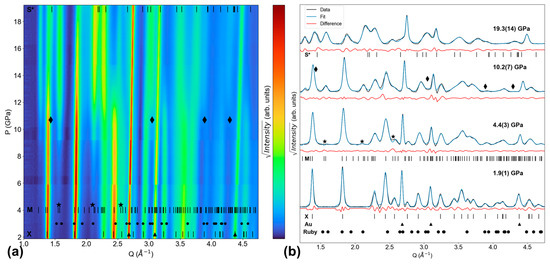
Figure 5.
Tb-none XRD experiment. (a) Contour plot of all XRD patterns. (b) Select XRD patterns (initial, onset of monazite, onset of scheelite, final) and their LeBail fits. Monazite peaks emerge at 4.4(3) GPa. Scheelite peaks appear to emerge at 10.2(7) GPa. ‘X’, ‘M’, and ‘S*’ ticks show TbPO4 peak positions for the xenotime [19], monazite [26], and scheelite (simulated at 20.5 GPa) phases [19], respectively. Triangles, circles, stars, and diamonds denote the peak positions of gold [28], ruby [29], emerging monazite, and emerging scheelite, respectively.
At 10.2(7) GPa, new peaks emerge at Q = 1.43 Å−1, 3.05 Å−1, 3.89 Å−1, and 4.29 Å−1 (denoted by diamond symbols in Figure 5), and these peaks grow as pressure continues to increase. The phase giving rise to these peaks is likely scheelite-structured TbPO4, as Lopez-Solano et al. and Bose et al. both predicted scheelite would be the post-monazite phase of TbPO4, and scheelite has been experimentally observed in YPO4, TmPO4, YbPO4, LuPO4, and ScPO4 [19,38,39,40]. Figure 5 also shows ‘S*’ ticks, which represent the peak positions of a scheelite TbPO4 structure simulated at 20.5 GPa, as reported by Lopez-Solano et al. [19]. The diamond symbols are not perfectly aligned with the S* ticks; however, this slight misalignment is expected given the differences in conditions between this experimental study and Lopez-Solano et al.’s simulation (e.g., pressure, stress state, temperature, and the confounding effects of these factors on individual peak positions). Therefore, the emergence of new peaks (diamond symbols) and their proximity to the ‘S*’ ticks suggests the presence of scheelite is plausible and requires confirmation via further XRD experiments. If confirmed, 10.2(7) GPa would be the lowest pressure at which any scheelite structure has been reported in REPO4s to date.
The final scan in this experiment contains xenotime, monazite, gold, and potentially scheelite. Therefore, this experiment yields a xenotime–monazite phase coexistence range of at least 14.9(14) GPa and a potential xenotime–monazite–scheelite phase coexistence range of at least 9.1(14) GPa.
A Dy-none experiment was also performed to build on our prior DyPO4 study, in which KCl was the only PTM tested that was solid at 1 atm [9]. Figure 6a shows XRD pattern evolution throughout the entire experiment, while Figure 6b shows LeBail fit quality at Pinitial (3.1(2) GPa), at the xenotime–monazite Ponset (6.9(5) GPa), and at Pmax (10.4(7) GPa). The first scan in this experiment shows xenotime, gold (upward triangle symbol), and ruby (circle symbol) peaks. At 6.9(5) GPa, monazite peaks emerge at Q = 1.59 Å−1, 2.10 Å−1, and 2.57 Å−1 (as denoted by stars in Figure 5); these are the (110), (02), and (211) reflections, respectively. In the Ponset scan, the refined monazite lattice parameters are a = 6.187(3) Å, b = 6.603(2) Å, c = 6.783(5) Å, and β = 102.40(4)°. The final scan at 10.4(7) GPa contains xenotime, monazite, and gold. Consequently, the DyPO4 xenotime–monazite phase coexistence range is found to be at least 3.5(7) GPa.
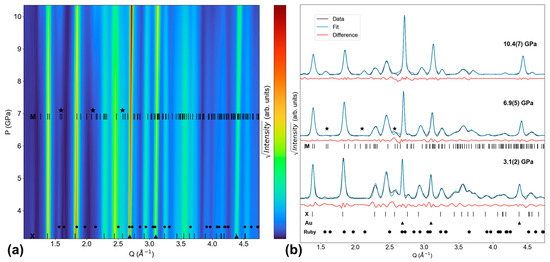
Figure 6.
Dy-none XRD experiment. (a) Contour plot of all XRD patterns. (b) Select XRD patterns (initial, onset of monazite, final) and their LeBail fits. Monazite peaks emerge at 6.9(5) GPa. ‘X’ and ‘M’ ticks show DyPO4 peak positions for the xenotime and monazite phases, respectively [25,26]. Triangles, circles, and stars denote the peak positions of gold [28], ruby [29], and emerging monazite, respectively.
Figure 7 summarizes the DyPO4 and TbPO4 phase behavior transformation data reported in this study as well as in two prior DyPO4 studies [7,9]. In the DyPO4 section, phase data from an experiment using the MEW PTM (Dy-MEW [7]) are shown, since a prior experiment using neon (Dy-neon [9]) did not reach pressures high enough to gauge the xenotime–monazite phase coexistence range. MEW has a hydrostatic limit of 10.5(5) GPa and is therefore hydrostatic at the xenotime–monazite Ponset, like neon. The Ponset from the Dy-neon experiment (9.1(1) GPa) is shown as an orange dashed line in Figure 7 and is within the error bar of the Ponset from the Dy-MEW experiment (9.6(7) GPa).
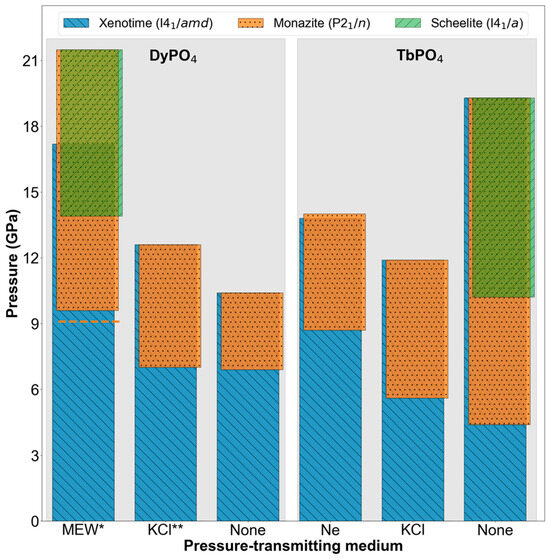
Figure 7.
High-pressure XRD-based phase map of DyPO4 and TbPO4, each tested with three different PTMs. The legend lists the phases with their corresponding space groups. For each REPO4-PTM combination, the upper limit of the highest bar(s) represents the highest pressure at which data are reported and does not represent a phase boundary. * The Dy-MEW data were originally reported by Sharma et al. [7]. The dashed orange line shows the DyPO4 xenotime–monazite Ponset value using neon PTM [9]. ** The Dy-KCl data were originally reported by Sharma et al. [9].
Figure 7 shows DyPO4 and TbPO4 both exhibit xenotime–monazite Ponset reductions with non-hydrostatic PTMs. Shear can facilitate the plastic deformation involved in phase transformation (i.e., polyhedral rotations and translations) and thereby reduce the hydrostatic pressure required to induce phase transformation. In fact, non-hydrostatic conditions have been suggested to lower the pressure required to induce mechanical instability in other REPO4 and REVO4 materials [41,42]. High-pressure dynamical instability (i.e., the softening of Raman-active and silent phonon modes) has also been observed in these materials, but it has less influence on Ponset than mechanical instability does [36,41,42]. In addition, the TbPO4 Ponset values are marginally (KCl) or significantly (none) lower than those of DyPO4 in the same PTM. TbPO4 Ponset values being lower likely stems from the monazite phase being more thermodynamically favorable in TbPO4 than in DyPO4 regardless of the kinetic barriers involved [33,34,35,36].
Figure 7 also shows the onset of the scheelite phase at 13.9(10) GPa in the Dy-MEW experiment and at 10.2(7) GPa in the Tb-none experiment. This difference in scheelite Ponset values is likely a convolution of compositional and shear effects. Because the Tb-none experiment is less hydrostatic than the Dy-MEW experiment, the onset pressure of the scheelite phase in the former experiment is expected to be lower. This expectation is consistent with observations from the other experiments. However, the effect of composition on the onset of the scheelite phase remains unclear. Moreover, the lack of scheelite (green bars) in the other four experiments shown in Figure 7 may simply be a consequence of those four experiments not reaching sufficiently high pressures. Considering strictly the DyPO4 experiments, we expect the scheelite Ponset to be lower in Dy-KCl and Dy-none than in Dy-MEW (as MEW is the most hydrostatic medium of the three) based on a hypothesis of shear-induced lowering of transformation pressure. Unfortunately, the Dy-KCl and Dy-none experiments terminated at pressures significantly lower than the scheelite Ponset of Dy-MEW, leaving significant untested pressure ranges in which the onset of scheelite is still plausible. Considering the TbPO4 experiments, the emergence of scheelite in Tb-none evidently shows a shear-induced lowering of Ponset because scheelite is not observed at the same pressure in lower shear experiments (i.e., Tb-neon, Tb-KCl). These lower shear experiments are expected to yield higher scheelite Ponset values than Tb-none, so the lack of scheelite observation may be attributable to an insufficient Pmax. In order to clarify the presence of scheelite, additional Dy-KCl, Dy-none, Tb-neon, and Tb-KCl experiments going to higher pressures are merited.
Next, the effect of shear on xenotime–monazite phase coexistence is considered. All experiments shown in Figure 7 show significant phase coexistence ranges of at least 3 GPa, further supporting the notion that REPO4 phase transformations are diffusional rather than martensitic. Consistent with our prior DyPO4 studies, the coexistence of multiple REPO4 phases at certain pressures defies Gibbs’ phase rule and further shows the sluggish nature of pressure-induced phase transformation in these materials [7,9]. Furthermore, the TbPO4 experiments show that while shear induces earlier onset of transformation, it does not induce earlier completion of transformation. While the xenotime–monazite coexistence range is 5.0(10) GPa in the Tb-neon experiment, this range extends to at least 6.3(8) GPa and at least 14.9(14) GPa in the Tb-KCl and Tb-none experiments, respectively. This range extension has also been reported in BaSO4 and α-Ti when these materials are compressed using non-hydrostatic PTMs [18,19]. At a fundamental level, extended phase coexistence under shear may be attributable to non-uniform stress fields causing varying degrees of transformation progression in a given volume of material. Conclusions regarding coexistence trends cannot be drawn from the DyPO4 experiments, as the Dy-KCl and Dy-none experiments do not go to sufficiently high pressures. For completeness, plots showing the pressure-dependence of TbPO4 and DyPO4 monazite and xenotime lattice parameters as well as a table of axial compressibilities are provided in the Supplementary Materials.
The findings in this study provide key insights for understanding REPO4s under complex stress states and inform potential structural applications, including CMC fiber coatings. This work provides in situ evidence to corroborate ex situ observations of phase transformation of TbPO4 under shear from other types of experiments (e.g., indentation, fiber pull-out) [4,5]. In addition, this study shows a high-shear environment can lower the Ponset to pressures below the xenotime REPO4′s hardness, suggesting transformation-related strain-hardening affects measured hardness values [4,43]. Moreover, this work suggests REPO4 compositions further from the xenotime–monazite phase boundary (i.e., with higher hydrostatic Ponset values) may be considered for CMC fiber coating applications if Ponset is proven to drop as dramatically under shear as it does in TbPO4. The benefits of REPO4 phase transformation (i.e., enhanced CMC plasticity and toughening) may be accessible at lower pressures and over a wider range of pressures than previously understood.
4. Conclusions
This study systematically probes the effect of non-hydrostaticity on the pressure-induced phase transformations of xenotime TbPO4 using in situ DAC XRD. Our prior DyPO4 study found non-hydrostatic KCl PTM induces the xenotime–monazite phase transformation at a pressure ~22% lower than in hydrostatic media (e.g., neon, 16:3:1 MEW) [9]. In this work, our experiments with three PTMs (neon, KCl, and none) show a lowering of the TbPO4 xenotime–monazite Ponset from 8.7(6) GPa to 5.6(4) GPa to 4.4(3) GPa, respectively. The Ponset value for TbPO4 with no PTM is the lowest value reported to date for any REPO4 and represents an almost 50% Ponset reduction in a high-shear stress state relevant to potential CMC applications. When comparing DyPO4 and TbPO4, the latter’s Ponset values are consistently lower; this fact is likely due to the monazite phase being more thermodynamically favorable in TbPO4 than in DyPO4. Lastly, our TbPO4 experiment with no PTM provides preliminary proof of scheelite as the high-pressure, post-monazite phase.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/solids5010008/s1. Details of sample powder synthesis; Figure S1: Scanning electron micrograph and energy-dispersive X-ray spectrum of TbPO4 sample powder; Figures S2–S5: Plots showing the pressure dependence of xenotime and monazite lattice parameters from the Tb-neon, Tb-KCl, Tb-none, and Dy-none experiments. Table S1 shows axial compressibilities of lattice parameters from all experiments. Table S2 shows R-values of LeBail fits from Figure 2b, Figure 4b, Figure 5b and Figure 6b. Table S3 shows bulk modulus values obtained from 3rd order Birch-Murnaghan equation of state fits.
Author Contributions
Conceptualization, J.S. and C.E.P.; data curation, J.S. and C.E.P.; formal analysis, J.S.; writing—original draft preparation, J.S.; writing—review and editing, J.S. and C.E.P.; supervision, C.E.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Science Foundation under Award No. DMR- 1352499. J.S. was supported by the Department of Defense through the National Defense Science & Engineering Graduate Fellowship Program. This work was performed at Beamline 12.2.2, Advanced Light Source, Berkeley National Laboratory. Beamline 12.2.2 is partially supported by COMPRES, the Consortium for Materials Properties Research in Earth Sciences under NSF Cooperative Agreement EAR 1606856. The Advanced Light Source is supported by the Director, Office of Science, Office of Basic Energy Sciences, U.S. Department of Energy under Contract No. DE-AC02-05CH11231.
Data Availability Statement
All relevant data that support the findings of this study are available from the corresponding authors upon request.
Acknowledgments
This work was performed at Beamline 12.2.2, Advanced Light Source, Berkeley National Laboratory. The authors thank the beamline scientists: Martin Kunz, Kathrin Armstrong, and Bora Kalkan. The authors also greatly appreciate the assistance of John Copley and Tom Duffy at Princeton University in providing diamond anvil cells and invaluable support while preparing for and performing experiments. In addition, the authors thank Ivar Reimanis for lending his diamond anvil cell for beamline experiments. Moreover, the authors thank Henry Afful for helping perform experiments as well as Matthew Musselman for synthesizing the DyPO4 sample. This research was supported by the National Science Foundation under Award No. DMR-1352499. J.S. was supported by the Department of Defense through the National Defense Science & Engineering Graduate Fellowship Program. Beamline 12.2.2 is partially supported by COMPRES, the Consortium for Materials Properties Research in Earth Sciences under NSF Cooperative Agreement EAR 1606856. Beamline 12.2.2 at the Advanced Light Source is a DOE Office of Science User Facility under contract no. DE-AC02-05CH11231.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Seydoux-Guillaume, A.M.; de Resseguier, T.; Montagnac, G.; Reynaud, S.; Leroux, H.; Reynard, B.; Cavosie, A.J. Bridging the Shocked Monazite Gap—Deformation Microstructures in Natural and Laser Shock-Loaded Samples. Earth Planet. Sci. Lett. 2022, 595, 117727. [Google Scholar] [CrossRef]
- Cox, M.A.; Cavosie, A.J.; Poelchau, M.; Kenkmann, T.; Bland, P.A.; Miljković, K. Shock Deformation Microstructures in Xenotime from the Spider Impact Structure, Western Australia. In Large Meteorite Impacts and Planetary Evolution VI; Geological Society of America: Boulder, CO, USA, 2021; pp. 449–464. [Google Scholar]
- Erickson, T.M.; Timms, N.E.; Pearce, M.A.; Cayron, C.; Deutsch, A.; Keller, L.P.; Kring, D.A. Shock-Produced High-Pressure (La, Ce, Th)PO4 Polymorph Revealed by Microstructural Phase Heritage of Monazite. Geology 2019, 47, 504–508. [Google Scholar] [CrossRef]
- Hay, R.S.; Boakye, E.E.; Mogilevsky, P.; Fair, G.E.; Parthasarathy, T.A.; Davis, J.E. Transformation Plasticity in (GdxDy1−x)PO4 Fiber Coatings During Fiber Push Out. J. Am. Ceram. Soc. 2013, 96, 1586–1595. [Google Scholar] [CrossRef]
- Hay, R.S.; Mogilevsky, P.; Boakye, E. Phase Transformations in Xenotime Rare-Earth Orthophosphates. Acta Mater. 2013, 61, 6933–6947. [Google Scholar] [CrossRef]
- Ni, Y.; Hughes, J.M.; Mariano, A.N. Crystal Chemistry of the Monazite and Xenotime Structures. Am. Mineral. 1995, 80, 21–26. [Google Scholar] [CrossRef]
- Sharma, J.; Afful, H.Q.; Packard, C.E. Phase Transformation Pathway of DyPO4 to 21.5 GPa. Crystals 2023, 13, 249. [Google Scholar] [CrossRef]
- Macey, B.J. The Crystal Chemistry of MTO4 Compounds with the Zicron, Scheelite, and Monazite Structure Types; Virginia Tech: Blacksburg, VA, USA, 2009. [Google Scholar]
- Sharma, J.; Musselman, M.; Haberl, B.; Packard, C.E. In Situ Synchrotron Diffraction of Pressure-Induced Phase Transition in DyPO4 under Variable Hydrostaticity. Phys. Rev. B 2021, 103, 184105. [Google Scholar] [CrossRef]
- Tschauner, O.; Ushakov, S.V.; Navrotsky, A.; Boatner, L.A. Phase Transformations and Indications for Acoustic Mode Softening in Tb-Gd Orthophosphate. J. Phys. Condens. Matter 2016, 28, 035403. [Google Scholar] [CrossRef] [PubMed]
- Lösch, H.; Hirsch, A.; Holthausen, J.; Peters, L.; Neumeier, S.; Huittinen, N. Site-Selective Fluorescence Spectroscopy Investigations of LnPO4 Xenotime Ceramics for Radioactive Waste Disposal; HZDR: Dresden, Germany, 2016; Volume 13. [Google Scholar]
- Santamaría-Pérez, D.; Gracia, L.; Garbarino, G.; Beltrán, A.; Chuliá-Jordán, R.; Gomis, O.; Errandonea, D.; Ferrer-Roca, C.; Martínez-García, D.; Segura, A. High-Pressure Study of the Behavior of Mineral Barite by X-ray Diffraction. Phys. Rev. B. 2011, 84, 054102. [Google Scholar] [CrossRef]
- Lacomba-Perales, R.; Errandonea, D.; Meng, Y.; Bettinelli, M. High-Pressure Stability and Compressibility of APO4 (A=La, Nd, Eu, Gd, Er, and Y) Orthophosphates: An X-ray Diffraction Study Using Synchrotron Radiation. Phys. Rev. B. 2010, 81, 064113. [Google Scholar] [CrossRef]
- Klotz, S.; Chervin, J.-C.; Munsch, P.; Le Marchand, G. Hydrostatic Limits of 11 Pressure Transmitting Media. J. Phys. D Appl. Phys. 2009, 42, 075413. [Google Scholar] [CrossRef]
- Uts, I.; Glazyrin, K.; Lee, K.K.M. Effect of Laser Annealing of Pressure Gradients in a Diamond-Anvil Cell Using Common Solid Pressure Media. Rev. Sci. Instrum. 2013, 84, 103904. [Google Scholar] [CrossRef] [PubMed]
- Dewaele, A.; Datchi, F.; Loubeyre, P.; Mezouar, M. High Pressure-High Temperature Equations of State of Neon and Diamond. Phys. Rev. B 2008, 77, 094106. [Google Scholar] [CrossRef]
- Dewaele, A.; Belonoshko, A.B.; Garbarino, G.; Occelli, F.; Bouvier, P.; Hanfland, M.; Mezouar, M. High-Pressure-High-Temperature Equation of State of KCl and KBr. Phys. Rev. B 2012, 85, 214105. [Google Scholar] [CrossRef]
- Errandonea, D.; Meng, Y.; Somayazulu, M.; Häusermann, D. Pressure-Induced α→ ω Transition in Titanium Metal: A Systematic Study of the Effects of Uniaxial Stress. Phys. B Condens. Matter 2005, 355, 116–125. [Google Scholar] [CrossRef]
- López-Solano, J.; Rodríguez-Hernández, P.; Muñoz, A.; Gomis, O.; Santamaría-Perez, D.; Errandonea, D.; Manjón, F.J.; Kumar, R.S.; Stavrou, E.; Raptis, C. Theoretical and Experimental Study of the Structural Stability of TbPO4 at High Pressures. Phys. Rev. B 2010, 81, 144126. [Google Scholar] [CrossRef]
- Shen, G.; Wang, Y.; Dewaele, A.; Wu, C.; Fratanduono, D.E.; Eggert, J.; Klotz, S.; Dziubek, K.F.; Loubeyre, P.; Fat’yanov, O.V.; et al. Toward an International Practical Pressure Scale: A Proposal for an IPPS Ruby Gauge (IPPS-Ruby2020). High Press. Res. 2020, 40, 299–314. [Google Scholar] [CrossRef]
- Anderson, O.L.; Isaak, D.G.; Yamamoto, S. Anharmonicity and the Equation of State for Gold. J. Appl. Phys. 1989, 65, 1534–1543. [Google Scholar] [CrossRef]
- Prescher, C.; Prakapenka, V.B. DIOPTAS: A Program for Reduction of Two-Dimensional X-ray Diffraction Data and Data Exploration. High Press. Res. 2015, 35, 223–230. [Google Scholar] [CrossRef]
- Degen, T.; Sadki, M.; Bron, E.; König, U.; Nénert, G. The High Score Suite. Powder Diffr. 2014, 29, S13–S18. [Google Scholar] [CrossRef]
- Le Bail, A. Whole Powder Pattern Decomposition Methods and Applications: A Retrospection. Powder Diffr. 2005, 20, 316–326. [Google Scholar] [CrossRef]
- Milligan, W.O.; Mullica, D.F.; Beall, G.W.; Boatner, L.A. The Structures of Three Lanthanide Orthophosphates. Inorganica Chim. Acta 1983, 70, 133–136. [Google Scholar] [CrossRef]
- Heuser, J.M.; Neumeier, S.; Peters, L.; Schlenz, H.; Bosbach, D.; Deissmann, G. Structural Characterisation of Metastable Tb- and Dy-Monazites. J. Solid State Chem. 2019, 273, 45–52. [Google Scholar] [CrossRef]
- Lösch, H.; Hirsch, A.; Holthausen, J.; Peters, L.; Xiao, B.; Neumeier, S.; Schmidt, M.; Huittinen, N. A Spectroscopic Investigation of Eu3+ Incorporation in LnPO4 (Ln = Tb, Gd1-XLuX, X = 0.3, 0.5, 0.7, 1) Ceramics. Front. Chem. 2019, 7, 94. [Google Scholar] [CrossRef]
- Couderc, J.J.; Garigue, G.; Lafourcade, L.; Nguyen, Q.T. Standard X-Ray Diffraction Powder Patterns. Z. Met. 1959, 50, 708–716. [Google Scholar]
- Jephcoat, A.P.; Hemley, R.J.; Mao, H.K. X-ray Diffraction of Ruby (Al2O3:Cr3+) to 175 GPa. Phys. B+C 1988, 150, 115–121. [Google Scholar] [CrossRef]
- Lebigot, E.O. Welcome to the Uncertainties Package—Uncertainties Python Package 3.0.1 Documentation. Available online: https://pythonhosted.org/uncertainties/ (accessed on 4 January 2024).
- Hemley, R.J.; Zha, C.S.; Jephcoat, A.P.; Mao, H.K.; Finger, L.W.; Cox, D.E. X-ray Diffraction and Equation of State of Solid Neon to 110 GPa. Phys. Rev. B 1989, 39, 11820–11827. [Google Scholar] [CrossRef] [PubMed]
- Finger, L.W.; Hazen, R.M.; Zou, G.; Mao, H.K.; Bell, P.M. Structure and Compression of Crystalline Argon and Neon at High Pressure and Room Temperature. Appl. Phys. Lett. 1981, 39, 892–894. [Google Scholar] [CrossRef]
- Ushakov, S.V.; Helean, K.B.; Navrotsky, A.; Boatner, L.A. Thermochemistry of Rare-Earth Orthophosphates. J. Mater. Res. 2001, 16, 2623–2633. [Google Scholar] [CrossRef]
- Ji, Y.; Kowalski, P.M.; Kegler, P.; Huittinen, N.; Marks, N.A.; Vinograd, V.L.; Arinicheva, Y.; Neumeier, S.; Bosbach, D. Rare-Earth Orthophosphates From Atomistic Simulations. Front. Chem. 2019, 7, 436276. [Google Scholar] [CrossRef] [PubMed]
- Mogilevsky, P. On the Miscibility Gap in Monazite-Xenotime Systems. Phys. Chem. Miner. 2007, 34, 201–214. [Google Scholar] [CrossRef]
- Musselman, M.A.; Wilkinson, T.M.; Haberl, B.; Packard, C.E. In Situ Raman Spectroscopy of Pressure-Induced Phase Transformations in Polycrystalline TbPO4, DyPO4, and GdxDy(1−x)PO4. J. Am. Ceram. Soc. 2018, 101, 2562–2570. [Google Scholar] [CrossRef]
- Froyen, S.; Cohen, M.L. Structural Properties of Nacl and Kc1 under Pressure. J. Phys. C Solid State Phys. 1986, 19, 2623–2632. [Google Scholar] [CrossRef]
- Bose, P.P.; Mittal, R.; Chaplot, S.L.; Loong, C.K.; Boatner, L.A. Inelastic Neutron Scattering, Lattice Dynamics, and High-Pressure Phase Stability of Zircon-Structured Lanthanide Orthophosphates. Phys. Rev. B. 2010, 82, 094309. [Google Scholar] [CrossRef]
- Zhang, F.X.; Wang, J.W.; Lang, M.; Zhang, J.M.; Ewing, R.C.; Boatner, L.A. High-Pressure Phase Transitions of ScPO4 and YPO4. Phys. Rev. B. 2009, 80, 184114. [Google Scholar] [CrossRef]
- Zhang, F.X.; Lang, M.; Ewing, R.C.; Lian, J.; Wang, Z.W.; Hu, J.; Boatner, L.A. Pressure-Induced Zircon-Type to Scheelite-Type Phase Transitions in YbPO4 and LuPO4. J. Solid State Chem. 2008, 181, 2633–2638. [Google Scholar] [CrossRef]
- Gomis, O.; Lavina, B.; Rodríguez-Hernández, P.; Muñoz, A.; Errandonea, R.; Errandonea, D.; Bettinelli, M. High-Pressure Structural, Elastic, and Thermodynamic Properties of Zircon-Type HoPO4 and TmPO4. J. Phys. Condens. Matter 2017, 29, 095401. [Google Scholar] [CrossRef]
- Marqueño, T.; Errandonea, D.; Pellicer-Porres, J.; Santamaría-Pérez, D.; Rodríguez-Hernández, P.; Muñoz, A. Competing Dynamical and Lattice Instabilities in RVO4 Rare-Earth Vanadium Oxides under High Pressure. Phys. Rev. Mater. 2022, 6, L060601. [Google Scholar] [CrossRef]
- Wilkinson, T.M.; Wu, D.; Musselman, M.A.; Li, N.; Mara, N.; Packard, C.E. Mechanical Behavior of Rare-earth Orthophosphates near the Monazite/Xenotime Boundary Characterized by Nanoindentation. Mater. Sci. Eng. A 2017, 691, 203–210. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).