Janus Particles in Acoustofluidic Setup: The Interplay between Self-Propulsion and Acoustic Trapping
Abstract
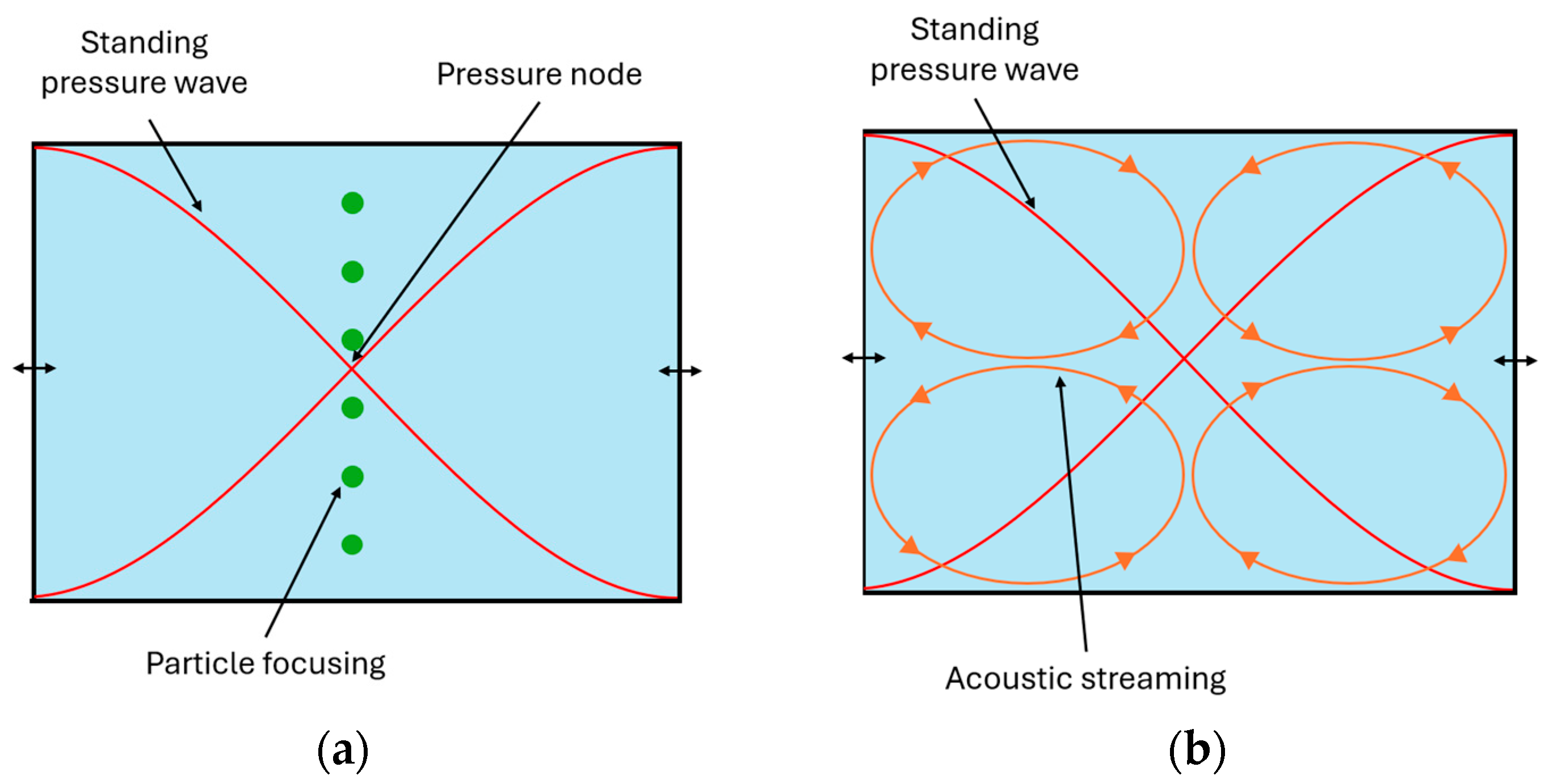
:1. Introduction
2. Materials and Methods
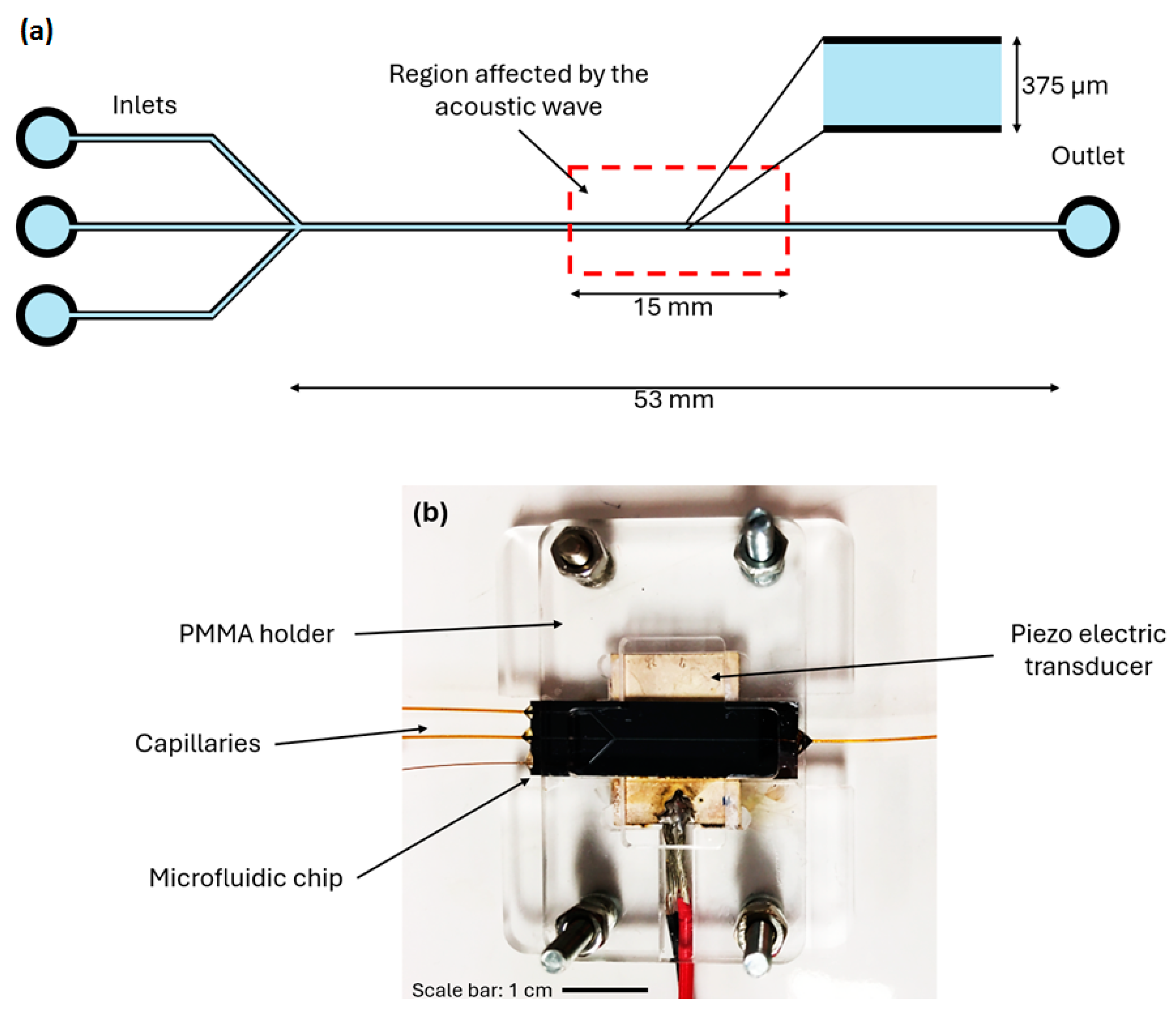
2.1. Chip Design
2.2. Experimental Setup
2.3. Janus Particles
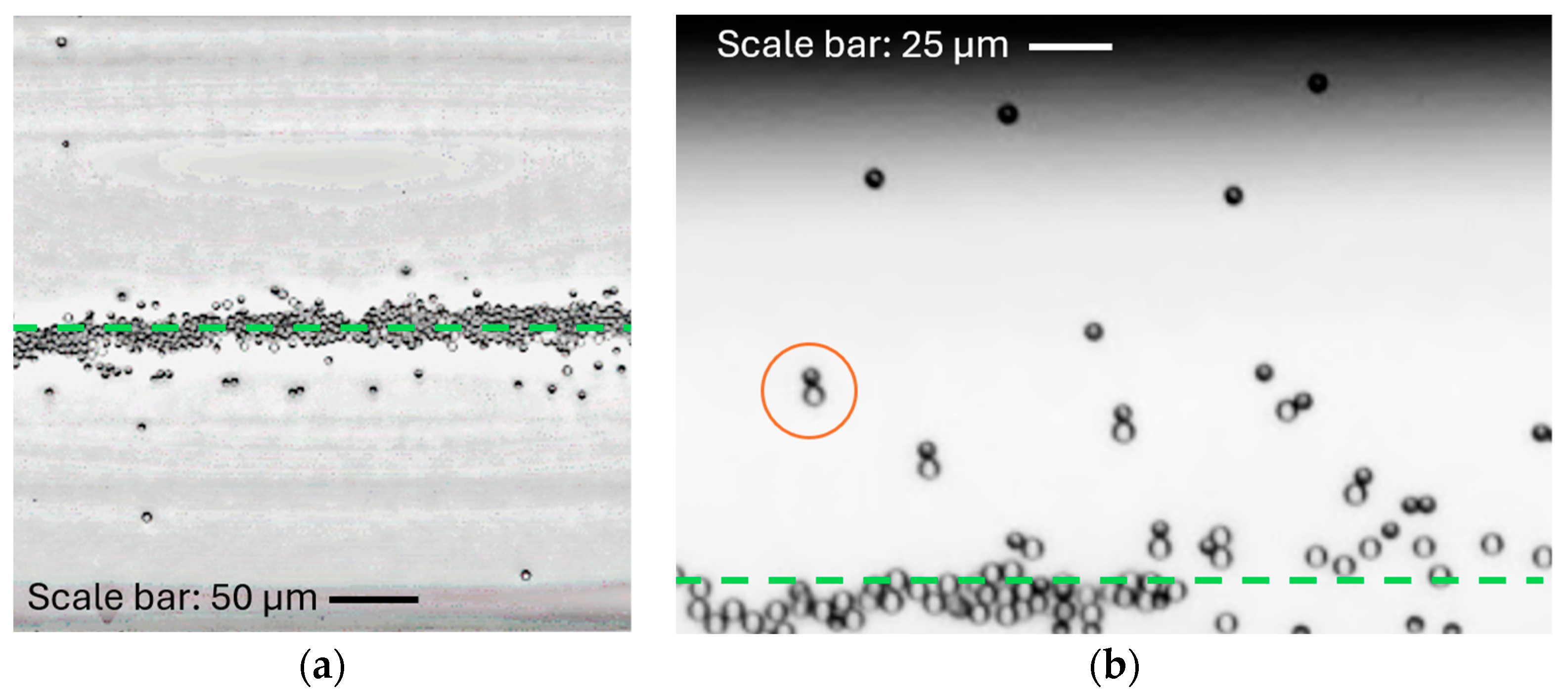
2.4. Experimental Procedure
3. Results
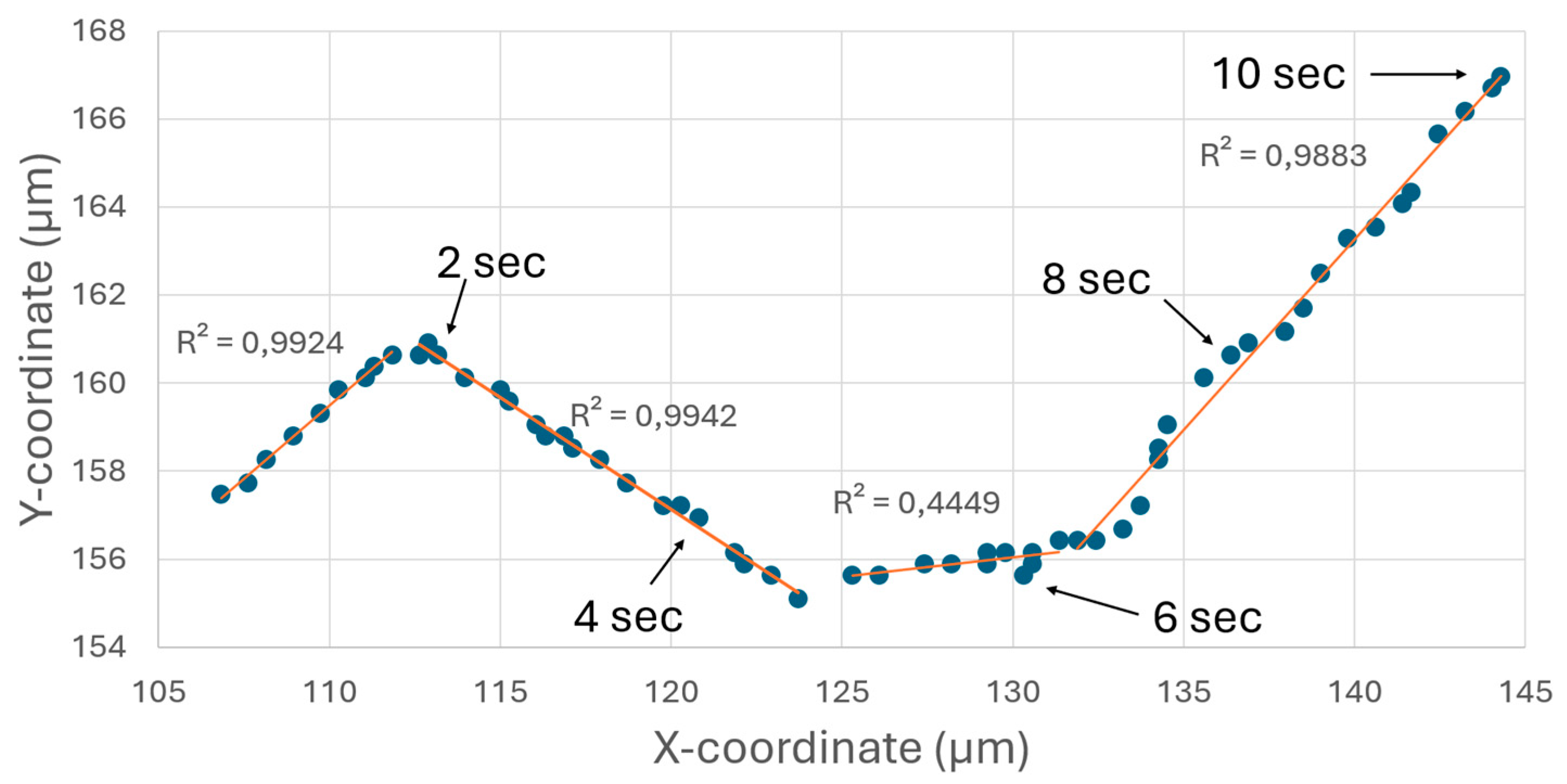
3.1. Self-Propelled Motion of Janus Particles and Motility
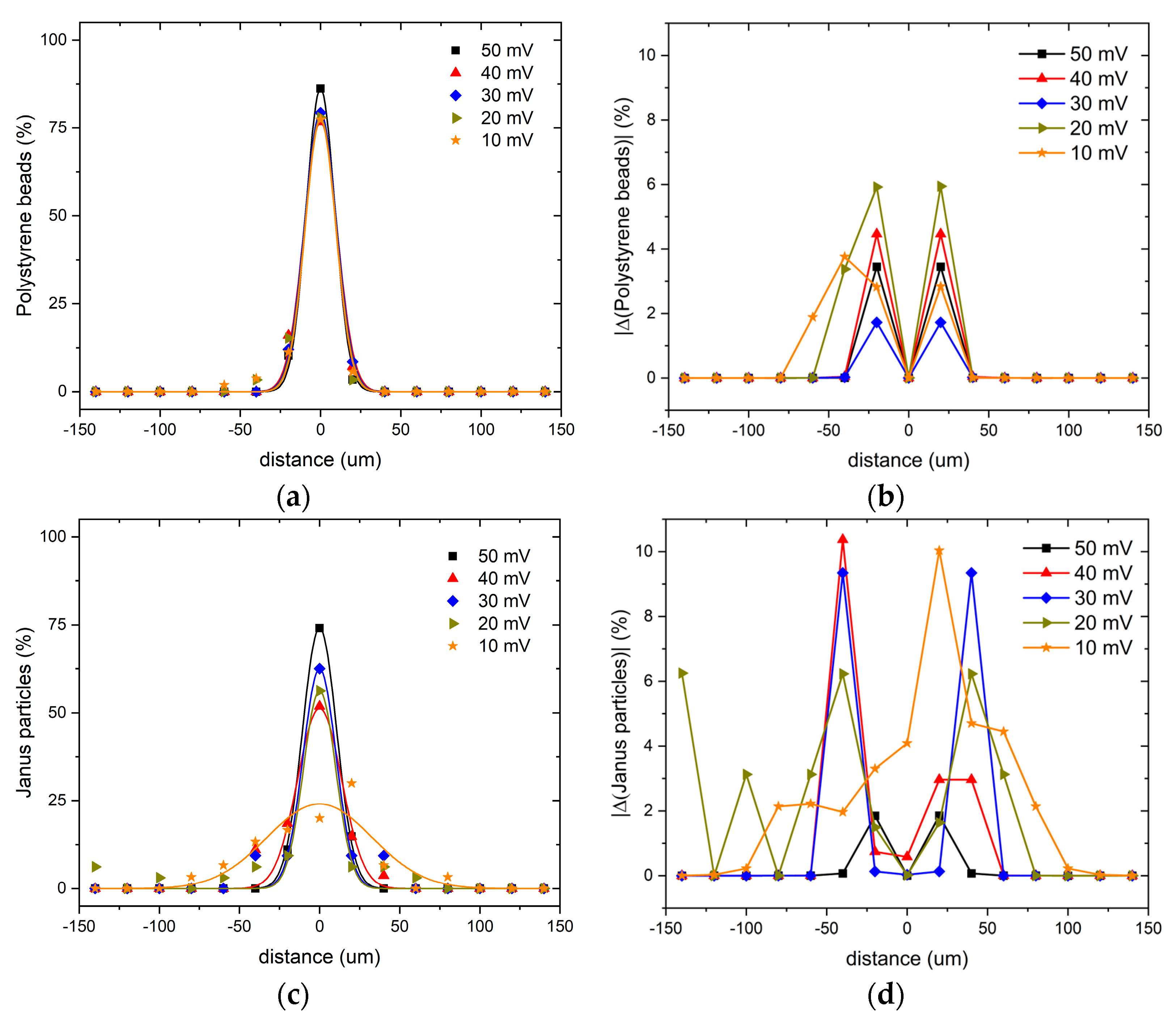
3.2. Escape of Motile Janus Particles from Acoustic Trap
3.3. Janus Particle-Aided Escape of Passive Beads from Acoustic Trap
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Beebe, D.J.; Mnesing, G.; Walker, G.B. Physics and Applications of Microfluidics in Biology. Annu. Rev. Biomed. Eng. 2002, 4, 261–286. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.; Li, P.; Lin, S.C.S.; Stratton, Z.S.; Nama, N.; Guo, F.; Slotcavage, D.J.; Mao, X.; Shi, J.; Costanzo, F.; et al. Surface acoustic wave microfluidics. Lab Chip 2013, 13, 3626. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.; Özçelik, A.; Rufo, J.; Wang, Z.; Fang, R.; Huang, T.J. Acoustofluidic separation of cells and particles. Microsyst. Nanoeng. 2013, 5, 32. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Wang, X.; Ren, J.; Lin, F.; Wu, J. Recent advances in acoustofluidic separation technology in biology. Microsyst. Nanoeng. 2022, 8, 94. [Google Scholar] [CrossRef] [PubMed]
- Kulkarni, M.B.; Goel, S. Mini-thermal platform integrated with microfluidic device with on-site detection for real-time DNA amplification. BioTechniques 2023, 74, 158–171. [Google Scholar] [CrossRef] [PubMed]
- Rufo, J.; Cai, F.; Friend, J.; Wiklund, M.; Huang, T.J. Acoustofluidics for biomedical applications. Nat. Rev. Methods Primers 2022, 2, 30. [Google Scholar] [CrossRef]
- Lam, K.H.; Liu, Y.; Li, Y.; Lim, H.G.; Zhou, Q.; Shung, K.K. Multifunctional single beam acoustic tweezer for non-invasive cell/organism manipulation and tissue imaging. Sci. Rep. 2016, 6, 37554. [Google Scholar] [CrossRef]
- Zhang, P.; Bachman, H.; Özçelik, A.; Huang, T.J. Acoustic microfluidics. Annu. Rev. Anal. Chem. 2020, 13, 17–43. [Google Scholar] [CrossRef]
- Li, P.; Mao, Z.; Peng, Z.; Zhou, L.; Chen, Y.; Huang, P.; Truica, C.I.; Drabick, J.J.; El-Deiry, W.S.; Dao, M.; et al. Acoustic separation of circulating tumor cells. Proc. Natl. Acad. Sci. USA 2015, 112, 4970–4975. [Google Scholar] [CrossRef]
- Collins, D.; Devendran, C.; Ma, Z.; Ng, J.W.; Neild, A.; Ai, Y. Acoustic tweezers via sub-time-of-flight regime surface acoustic waves. Sci. Adv. 2016, 2, e1600089. [Google Scholar] [CrossRef]
- Ahmed, D.; Özçelik, A.; Bojanala, N.; Nama, N.; Upadhyay, A.; Chen, Y.; Hanna-Rose, W.; Huang, T.J. Rotational manipulation of single cells and organisms using acoustic waves. Nat. Commun. 2016, 7, 11085. [Google Scholar] [CrossRef]
- Yunus, D.E.; Sohrabi, S.; He, R.; Shi, W.; Liu, Y. Acoustic patterning for 3D embedded electrically conductive wire in stereolithography. J. Micromechanics Microengineering 2017, 27, 045016. [Google Scholar] [CrossRef]
- Park, J.; Jung, J.H.; Destgeer, G.; Ahmed, H.; Park, K.; Sung, H.J. Acoustothermal tweezer for droplet sorting in a disposable microfluidic chip. Lab Chip 2017, 17, 1031–1040. [Google Scholar] [CrossRef] [PubMed]
- Muller, P.B.; Bruus, H. Numerical study of thermoviscous effects in ultrasound-induced acoustic streaming in microchannels. Phys. Rev. E 2014, 90, 043016. [Google Scholar] [CrossRef] [PubMed]
- Gelin, P.; Sukas, Ö.S.; Hellemans, K.; Maes, D.; De Malsche, W. Study on the mixing and migration behavior of micro-size particles in acoustofluidics. Chem. Eng. J. 2019, 369, 370–375. [Google Scholar] [CrossRef]
- Howse, J.R.; Jones, R.; Ryan, A.J.; Gough, T.; Vafabakhsh, R.; Golestanian, R. Self-Motile colloidal particles: From directed propulsion to random walk. Phys. Rev. Lett. 2007, 99, 048102. [Google Scholar] [CrossRef]
- Baraban, L.; Makarov, D.; Schmidt, O.G.; Cuniberti, G.; Leiderer, P.; Erbe, A. Control over Janus micromotors by the strength of a magnetic field. Nanoscale 2013, 5, 1332–1336. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, P.K.; Zhou, Y.; Li, Y.; Marchesoni, F.; Nori, F. Binary Mixtures in Linear Convection Arrays. ChemPhysChem 2022, 24, e202200471. [Google Scholar] [CrossRef]
- Bag, P.; Nayak, S.; Debnath, T.; Ghosh, P.K. Directed Autonomous Motion and Chiral Separation of Self-Propelled Janus Particles in Convection Roll Arrays. J. Phys. Chem. Lett. 2022, 13, 11413–11418. [Google Scholar] [CrossRef]
- Li, Y.; Li, L.; Marchesoni, F.; Debnath, T.; Ghosh, P.K. Diffusion of chiral Janus particles in convection rolls. Phys. Rev. Res. 2020, 2, 013250. [Google Scholar] [CrossRef]
- Ghosh, P.K.; Marchesoni, F.; Li, Y.; Nori, F. Active particle diffusion in convection roll arrays. Phys. Chem. Chem. Phys. 2021, 23, 11944–11953. [Google Scholar] [CrossRef]
- Debnath, T.; Chaudhury, P.; Mukherjee, T.; Mondal, D.; Ghosh, P.K. Escape kinetics of self-propelled particles from a circular cavity. J. Chem. Phys. 2021, 155, 194102. [Google Scholar] [CrossRef]
- Wang, X.; Liu, M.; Jing, D.; Prezhdo, O. Generating Shear Flows without Moving Parts by Thermo-osmosis in Heterogeneous Nanochannels. J. Phys. Chem. Lett. 2021, 12, 10099–10105. [Google Scholar] [CrossRef]
- Baraban, L.; Tasinkevych, M.; Popescu, M.N.; Sánchez, S.; Dietrich, S.; Schmidt, O.G. Transport of cargo by Catalytic Janus Micro-motors. Soft Matter 2012, 8, 48–52. [Google Scholar] [CrossRef]
- Yu, H.; Kopach, A.; Misko, V.R.; Vasylenko, A.A.; Marchesoni, F.; Nori, F.; Makarov, D.; Baraban, L.; Cuniberti, G. Confined catalytic Janus swimmers: Geometry-driven rectification transients and directional locking. Small 2016, 12, 5882–5890. [Google Scholar] [CrossRef]
- Ghosh, P.K.; Misko, V.R.; Marchesoni, F.; Nori, F. Self-Propelled Janus Particles in a Ratchet: Numerical Simulations. Phys. Rev. Lett. 2013, 110, 268301. [Google Scholar] [CrossRef]
- Lisin, E.A.; Vaulina, O.S.; Lisina, I.I.; Petrov, O.F. Active Brownian particle in homogeneous media of different viscosities: Numerical simulations. Phys. Chem. Chem. Phys. 2021, 23, 16248–16257. [Google Scholar] [CrossRef] [PubMed]
- Palacci, J.; Sacanna, S.; Steinberg, A.P.; Pine, D.J.; Chaikin, P.M. Living crystals of Light-Activated colloidal surfers. Science 2013, 339, 936–940. [Google Scholar] [CrossRef] [PubMed]
- Misko, V.R.; Baraban, L.; Makarov, D.; Huang, T.; Gelin, P.; Mateizel, I.; Wouters, K.; De Munck, N.; Nori, F.; De Malsche, W. Selecting active matter according to motility in an acoustofluidic setup: Self-propelled particles and sperm cells. Soft Matter 2023, 19, 8635. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benko, L.M.; Misko, V.R.; Baraban, L.; Makarov, D.; Maisto, A.; Malsche, W.D. Janus Particles in Acoustofluidic Setup: The Interplay between Self-Propulsion and Acoustic Trapping. Micro 2024, 4, 185-195. https://doi.org/10.3390/micro4010013
Benko LM, Misko VR, Baraban L, Makarov D, Maisto A, Malsche WD. Janus Particles in Acoustofluidic Setup: The Interplay between Self-Propulsion and Acoustic Trapping. Micro. 2024; 4(1):185-195. https://doi.org/10.3390/micro4010013
Chicago/Turabian StyleBenko, Lisa Marie, Vyacheslav R. Misko, Larysa Baraban, Denys Makarov, Antonio Maisto, and Wim De Malsche. 2024. "Janus Particles in Acoustofluidic Setup: The Interplay between Self-Propulsion and Acoustic Trapping" Micro 4, no. 1: 185-195. https://doi.org/10.3390/micro4010013
APA StyleBenko, L. M., Misko, V. R., Baraban, L., Makarov, D., Maisto, A., & Malsche, W. D. (2024). Janus Particles in Acoustofluidic Setup: The Interplay between Self-Propulsion and Acoustic Trapping. Micro, 4(1), 185-195. https://doi.org/10.3390/micro4010013







