The Second Quantum Revolution: Unexplored Facts and Latest News
Abstract
:1. Introduction
- Planck’s Quantum Theory (1900) [2]: the starting point of QM was Planck’s proposal that the energy of harmonic oscillators, such as those emitting electromagnetic radiation, cannot take any value save for discrete values called quanta.
- Bohr’s Atomic Model (1913) [3]: Bohr extended these concepts to atomic structure, proposing a model where electrons have quantized angular momentum and travel on quantized orbits.
- Schrödinger’s Wave Equation (1925) [4]: Schrödinger developed the wave equation, a fundamental equation describing the time-dependent evolution of a quantum state.
- Heisenberg’s Uncertainty Principle (1927) [5]: Heisenberg formulated the Uncertainty Principle, stating that it is impossible to simultaneously know with precision both the position and linear momentum of a particle.
- Einstein–Podolsky–Rosen Paradox (EPR) (1935) [6]: the EPR Paradox is based on quantum entanglement, a state where the properties of two particles are closely correlated even at large distances, thereby highlighting implications on the nature of reality.
- Bell inequality (1964) [7]: Bell formulated an inequality to establish limits on the correlations that can exist between measurements of entangled particles.
2. Entanglement: From Philosophy to the Basic Concept of Physics
“[…] that one body may act upon another at a distance through a vacuum without the mediation of any thing else by & through which their action or force may be conveyed from one to another is to me so great an absurdity that I believe no man who has in philosophical matters any competent faculty of thinking can ever fall into it.”Isaac Newton [11]
2.1. Einstein’s Attacks
- Postulate I
- Postulate II
- Postulate III
- Postulate IV
“In a complete theory there is an element corresponding to each element of reality. A sufficient condition for the reality of a physical quantity is the possibility of predicting it with certainty, without disturbing the system. In QM in the case of two physical quantities described by non-commuting operators, the knowledge of one precludes the knowledge of the other. Then either (1) the description of reality given by the wave function in QM is not complete or (2) these two quantities cannot have simultaneous reality. Consideration of the problem of making predictions concerning a system on the basis of measurements made on another system that had previously interacted with it leads to the result that if (1) is false then (2) is also false. One is thus led to conclude that the description of reality as given by a wave function is not complete.”
- Reality:If, without in any way disturbing a system, we can predict with certainty (i.e., with probability equal to unity) the value of a physical quantity, then there exists an element of physical reality corresponding to this physical quantity.”
- Completeness:“[...] every element of the physical reality must have counterpart in the physical theory.”
- Locality:“On the other hand, since at the time of measurement the two systems no longer interact, no real change can take place in the second system in consequence of anything that may be done to the first system.”
“While we have thus shown that the wave function does not provide a complete description of the physical reality, we left open the question of whether or not such a description exists. We believe, however, that such a theory is possible.”
2.2. To Bohr or Not to Bohr
“One could object to this conclusion on the grounds that our criterion of reality is not sufficiently restrictive. Indeed, one would not arrive at our conclusion if one insisted that two or more physical quantities can be regarded as simultaneous elements of reality only when they can be simultaneously measured or predicted. On this point of view, since either one or the other, but not both simultaneously, of the quantities P and Q can be predicted, they are not simultaneously real. This makes the reality of P and Q depend upon the process of measurement carried out on the first system, which does, not disturb the second system in any way. No reasonable definition of reality could be expected to permit this.”
2.3. The Bell Sentence
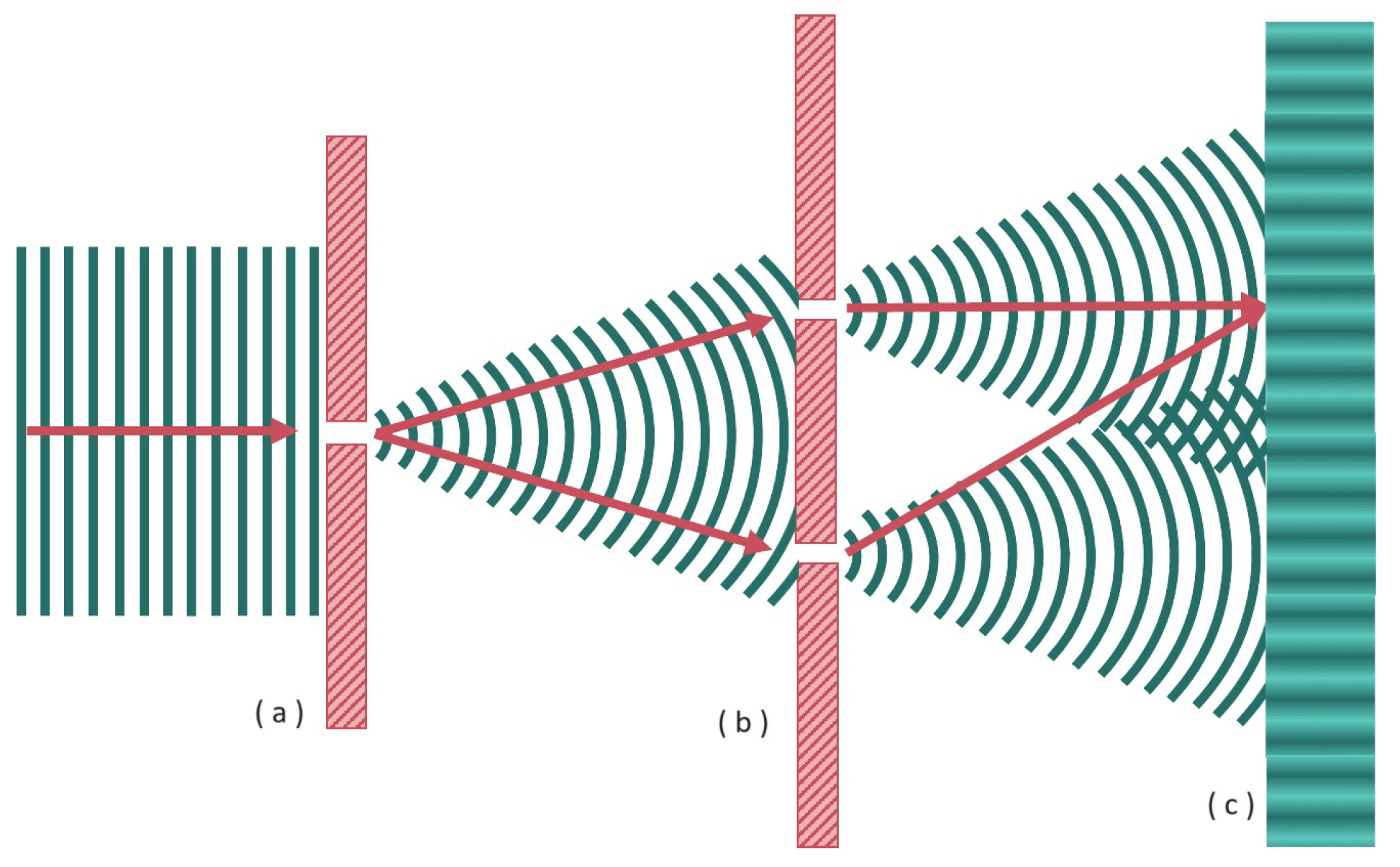
2.4. Back to Duality
3. Entanglement and Modern Physics Teaching
3.1. The EPR Paradox
3.2. Transitioning between Classical and Quantum Paradigms: From Classical Correlations to Entangled States
3.2.1. Introduction: Ideas to Introduce a New Paradigm
- If you know the state of a quantum system, you do not know everything there is to know about the system. In particular, it is not guaranteed that you can predict the outcome of an experiment. The state space of a quantum system is not a countable set, and, in a quantum system, states are not distinguishable from each other in a completely unambiguous way.
- Moreover, in a quantum system, it is not possible to perform an experiment (a measurement) that leaves the system undisturbed, regardless of how gentle the measurement itself might be. In essence, a quantum system, whether it is an electron, a photon, or a collection of atoms, does not have a well-defined state; more precisely, it exists in a condition of a superposition of states (in this regard, the “Schrödinger’s Cat Paradox” illustrates this concept well), which are all equally realizable in terms of stochastic probability. It is only through the measurement of a specific physical quantity associated with the system that it collapses into one of the possible states.
- These effects can be observed in quantum systems that are composed of a single particle, but they are not the only distinctions we can observe between systems composed of classical objects and quantum objects. There are additional differences that manifest in composite quantum systems that include at least two subsystems, each of a quantum nature. The correlations between these subsystems give rise to another distinction between classical and quantum systems as, while correlations in classical systems can always be described in terms of classical probabilities, this is not always possible in quantum composed systems. Such non-classical correlations lead to apparent paradoxes, like the famous EPR Paradox, which might suggest, at first glance, the existence of a remote and non-local action in QM. States that exhibit such non-classical correlations are referred to as entangled states.
3.2.2. Pure States
3.2.3. Bipartite Quantum Systems
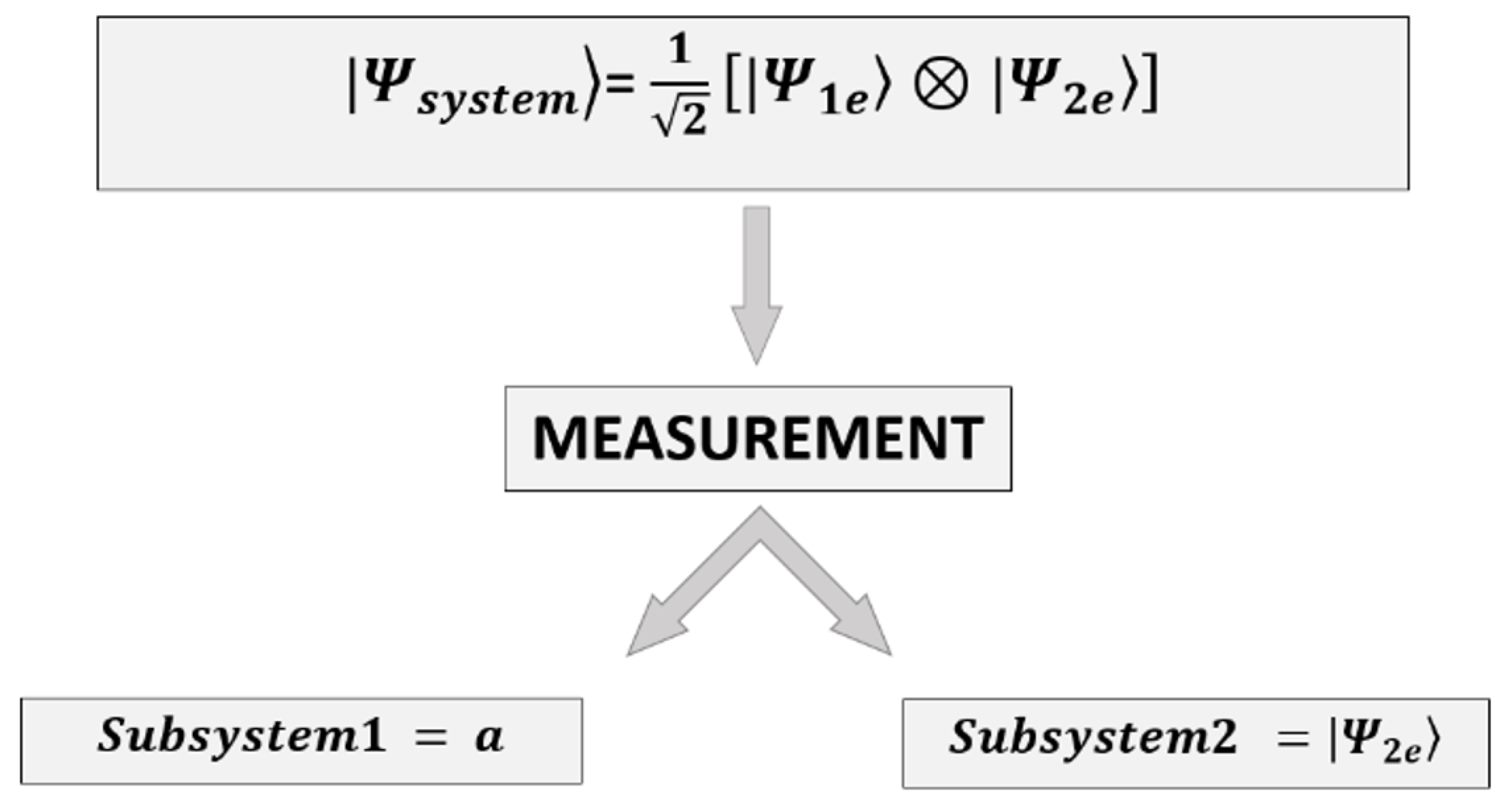
3.2.4. Entangled System
- Let us associate an amount of information, which is denoted as and , with the physical state of the two subsystems. The so-defined composite operation “•” will provide us with the measurement result for Subsystem 1 and the value for Subsystem 2 in the following manner:
- We observe that the measurement on the first subsystem will be a function of the information contained in the second , and vice versa.
- Preparation: The entangled system is prepared in a particular state, such as .
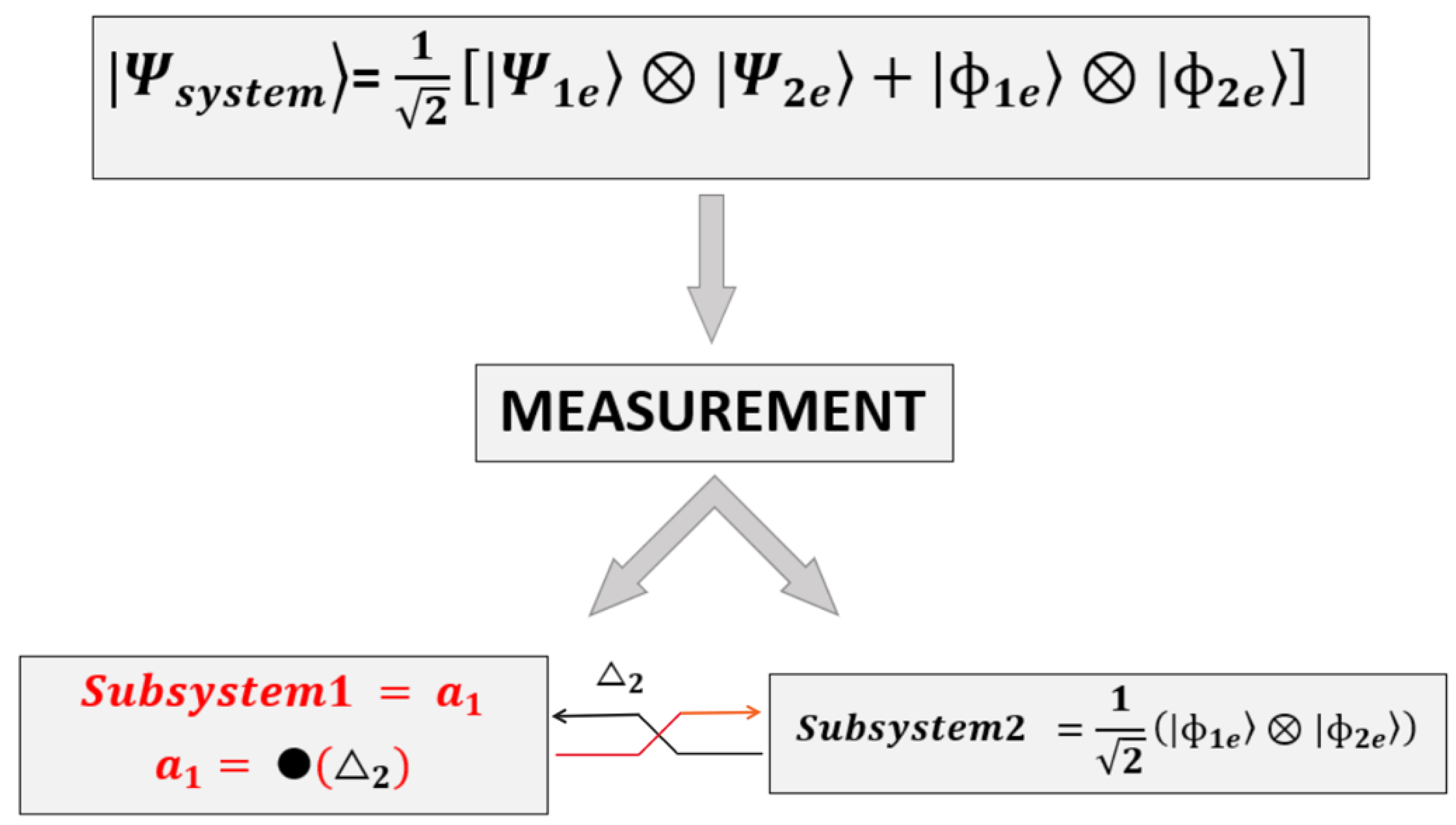
- Measurement Setup: Separate measurements are performed on each subsystem, which is indicated by the operators ⊗, +, and “•” in the context of QM.
- Quantum Interaction: The measurement on one subsystem influences the other, thereby causing a change in their states due to entanglement.
- Outcome: After the measurements, the specific values, and , are obtained for each subsystem.
- Correlations: The outcomes for each subsystem are correlated in such a way that they cannot be described independently; their behavior is intertwined.
- Entanglement Effect: The measurements on one subsystem provide information about the other, thereby defying classical concepts of independent measurements.
3.2.5. Summary
- (a)
- Instantaneous Correlations: Even when entangled particles are separated by large distances, any measurement made on one particle will instantaneously influence the state of the other, regardless of the distance. This phenomenon appears to violate the concept of causality in classical physics.
- (b)
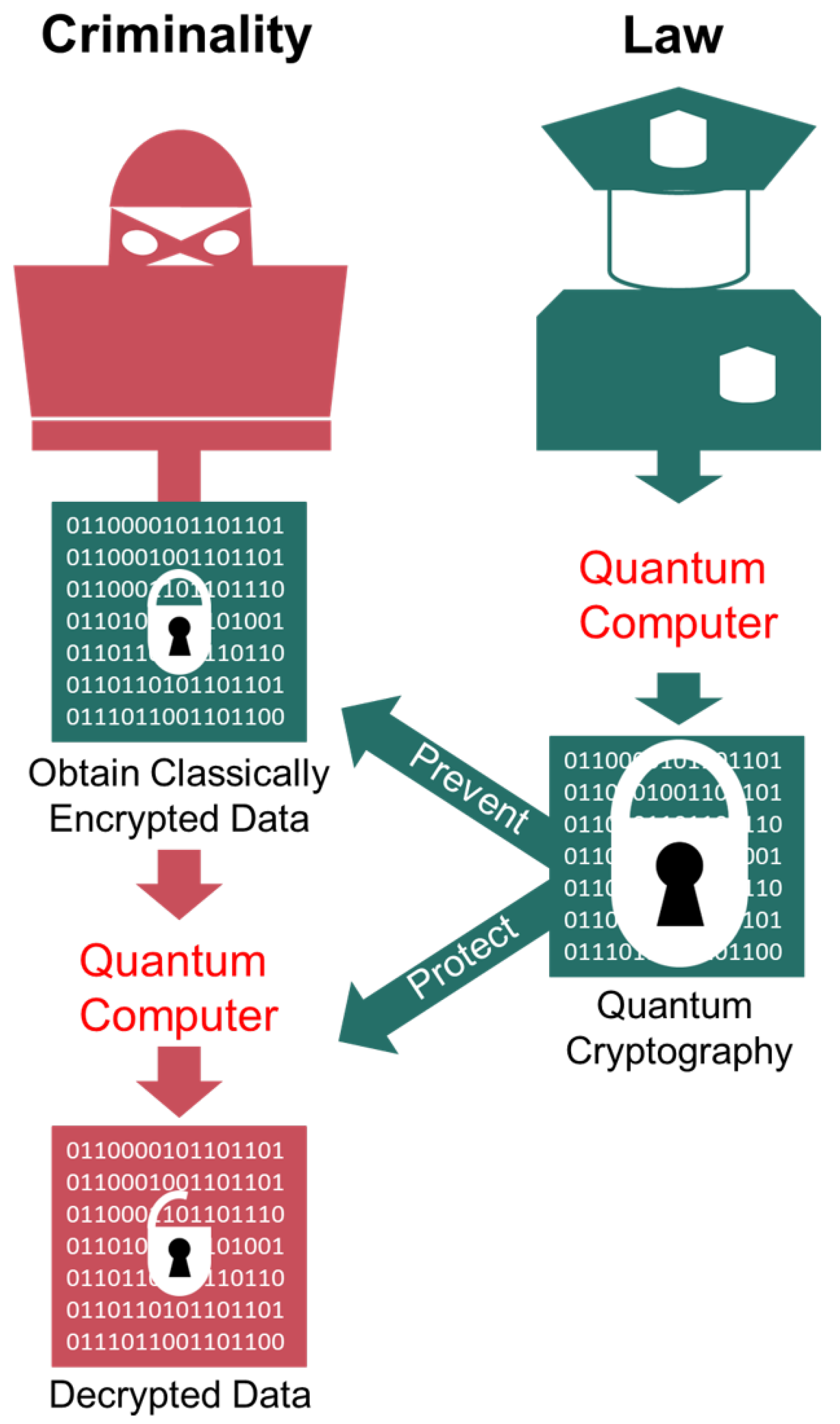
- Quantum Communication: Quantum entanglement can be harnessed for quantum communication, such as in the field of quantum cryptography. Changes to one entangled particle can be detected instantaneously by the other, thus allowing for the transmission of secure information.
- (c)
- Quantum Computing: Entanglement offers significant advantages in the field of quantum computing. Entangled qubits, which are qubits that are part of an entangled quantum system, can exist in combined states and perform complex operations in parallel, thereby potentially speeding up the solution of problems that are otherwise impossible for classical computers.
- (d)
- Representation of Quantum Reality: Entanglement demonstrates that the laws of QM can lead to results that seem counterintuitive or contrary to our everyday experience. This underscores the need to embrace a new conceptual paradigm when describing the world at the quantum level.
- (e)
- Quantum Thermal Engines: Theoretical concepts of quantum engines, though not yet practically implemented, leverage entanglement to explore innovative ways of enhancing efficiency in converting heat to work, thus challenging traditional conceptions of physical reality and paving the way for potential applications in the fields of thermodynamics and engineering [43].
3.3. Transitioning between Classical and Quantum Paradigms: Bell’s Inequality with Scratchcards
- If one scratches the corresponding square (i.e., with the same identifying letter, A, B, or C) on both halves, then the color revealed beneath is always the same. It is white 50% of the times and black the remaining 50% of the times.
- If one scratches different squares (i.e., squares identified by different letters) on two halves from the same ticket, one finds the same color only 25% of the time (with an equal probability for each color appearing) and different colors 75% of the time (with an equal probability of finding black on the half labeled 1 and white on the half labeled 2, and vice versa).
3.4. Summary
4. New Avenues for Quantum Technologies: Quantum Molecular Materials
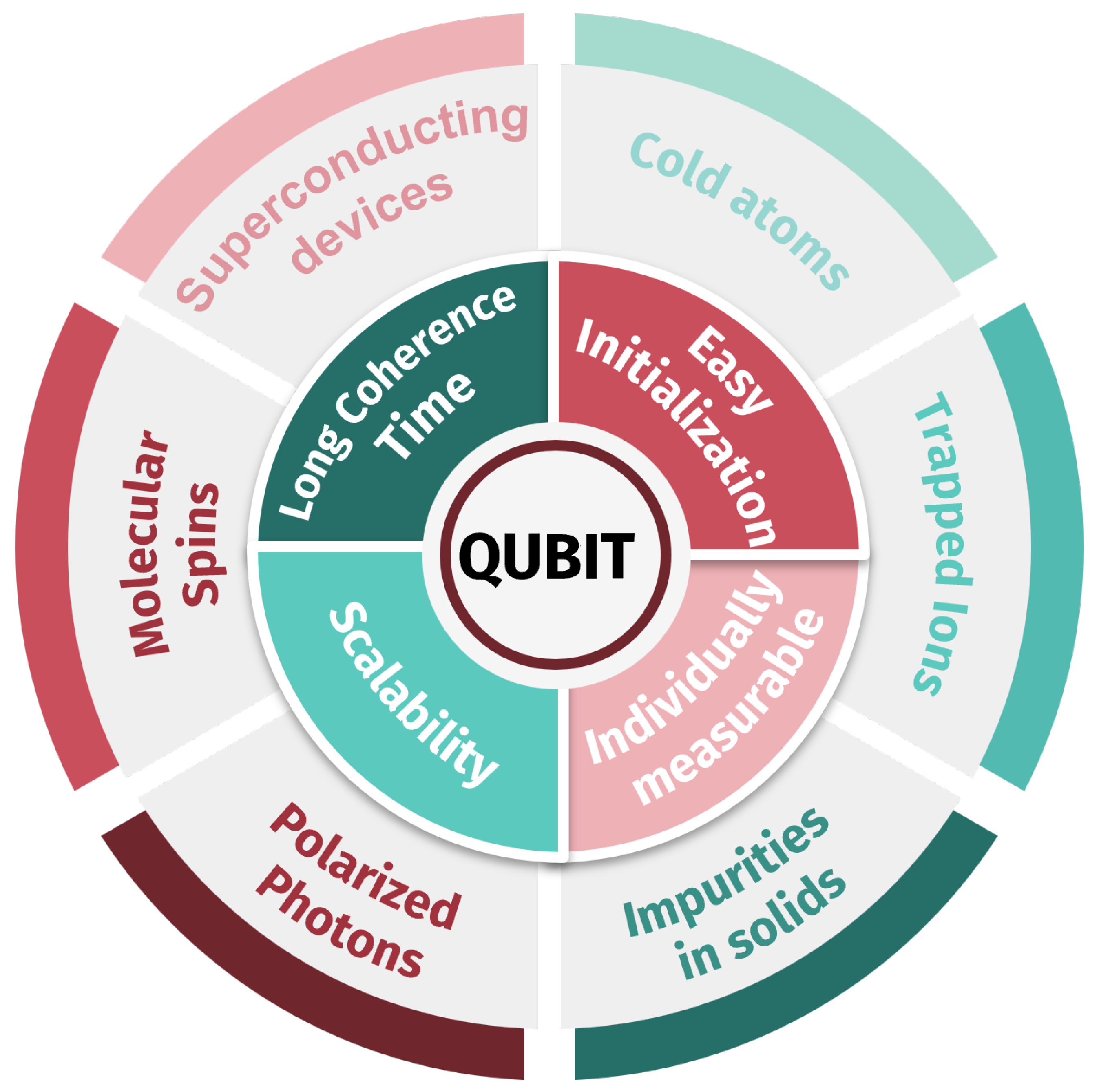
4.1. Molecular Chemistry in Quantum Technology
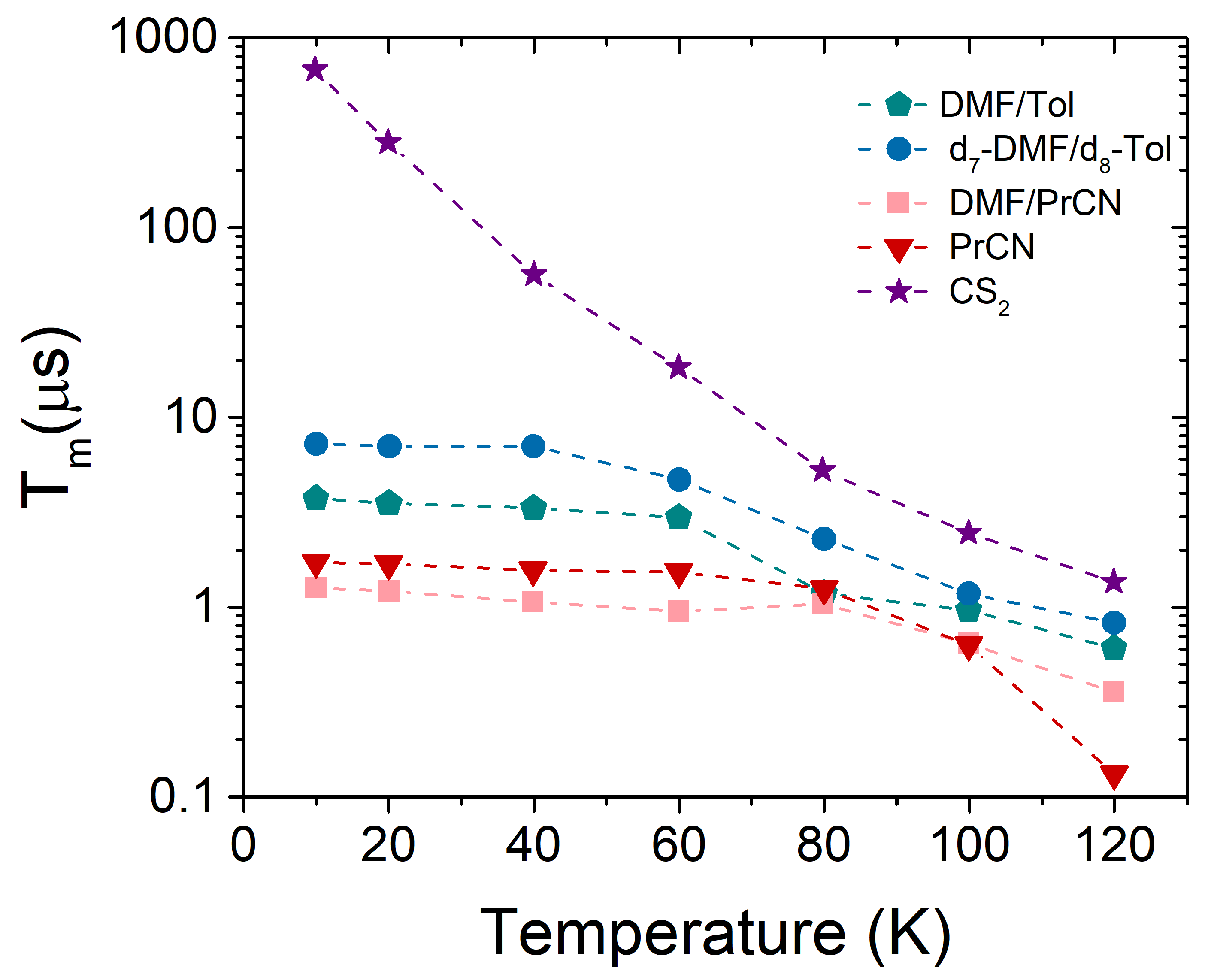
4.1.1. Coherence Time
4.1.2. Initialization
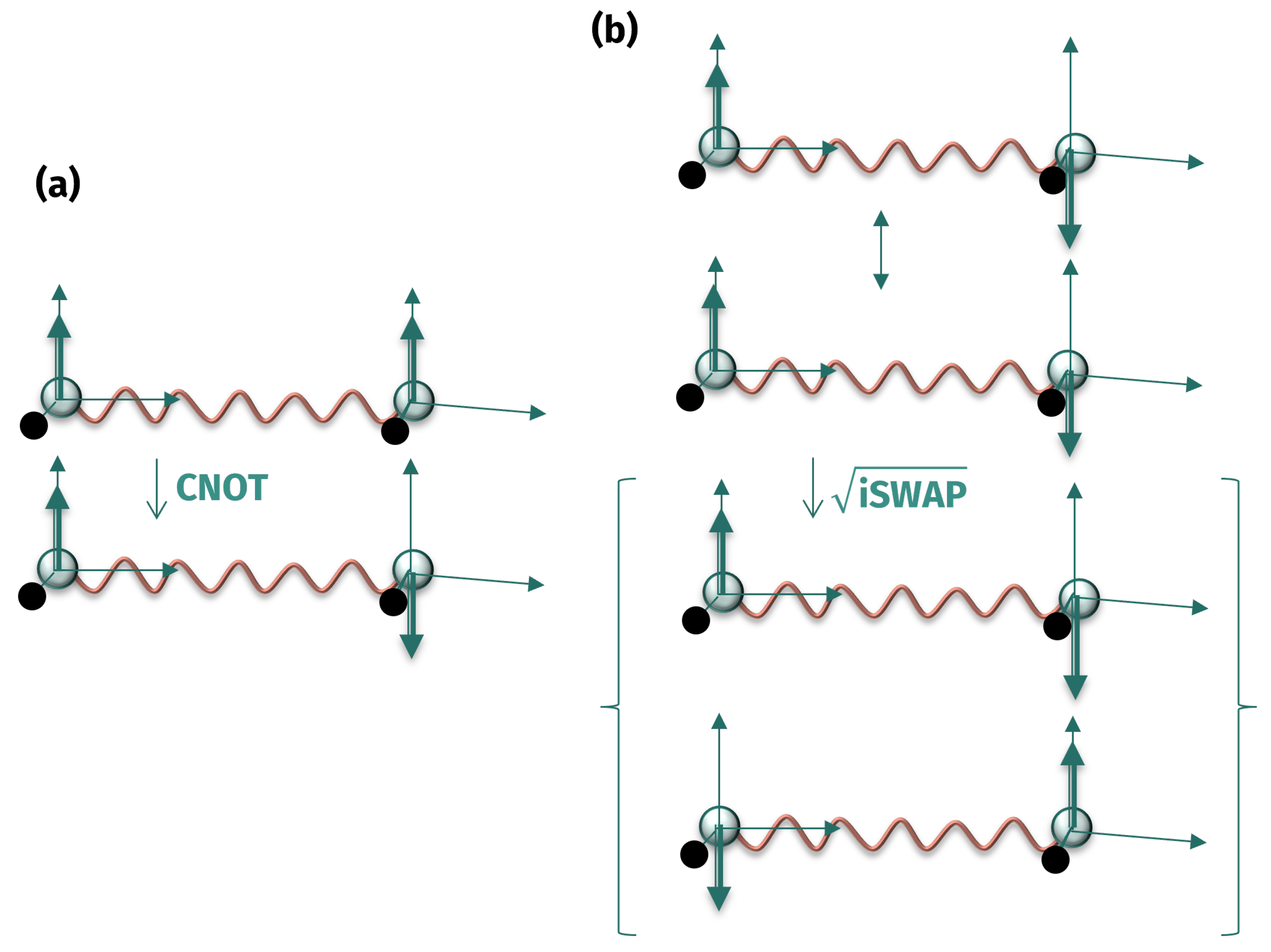
4.1.3. Quantum Gates
4.1.4. Addressability
4.1.5. Scalability
4.2. Molecular Spins in Hybrid Quantum Architectures
Magnetic Material–Superconductor Coupling
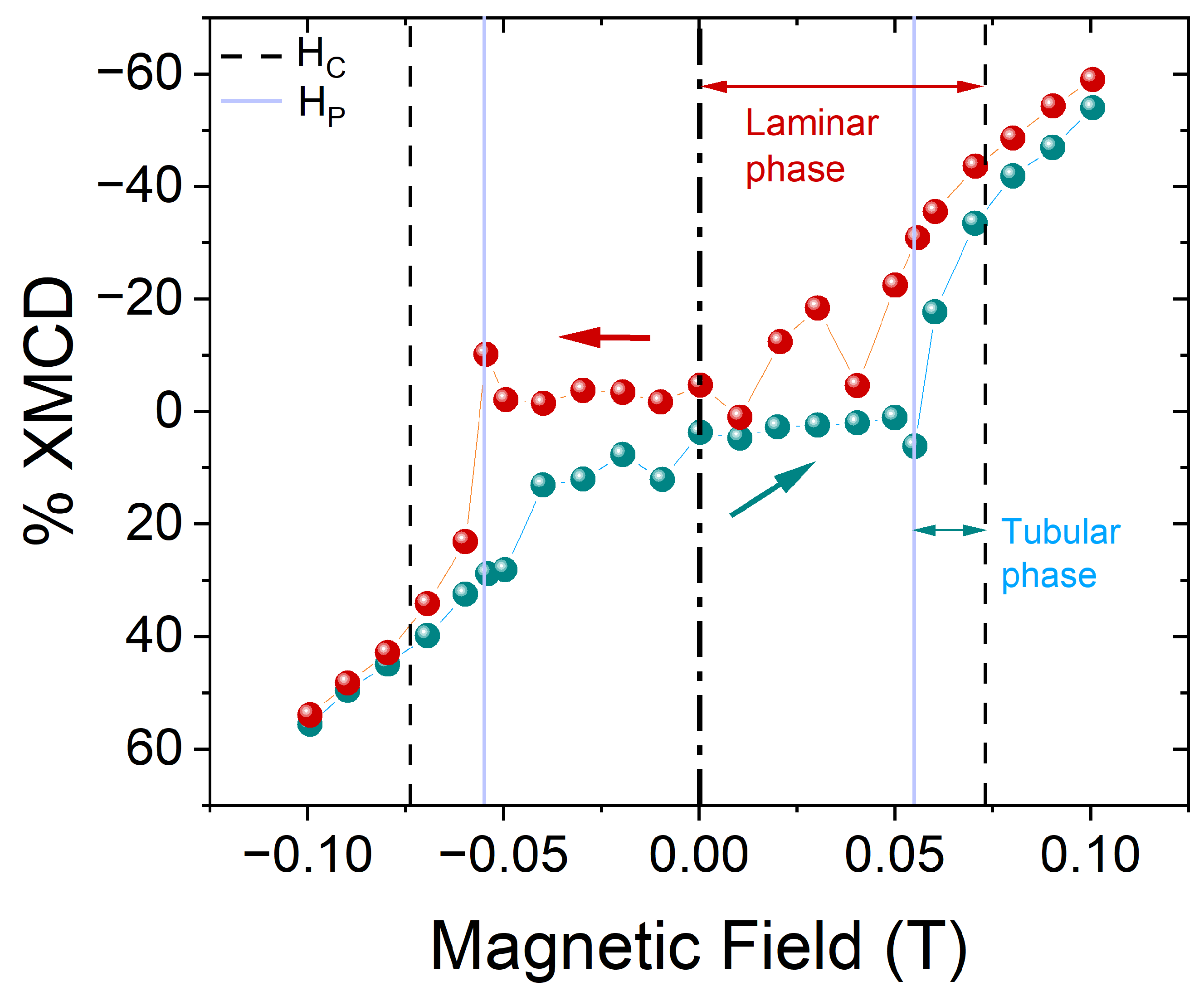
4.3. TbPc2 as the Local Sensor of the Superconductive Phase
4.4. Summary
5. Harnessing Quantum Complexity and Implications for Potential Industrial Applications
- Grid Optimization: Quantum algorithms can be employed to optimize the operation and control of power grids, thus ensuring efficient energy distribution and minimizing transmission losses [108].
- Renewable Energy Integration: Quantum computing can assist in optimizing the integration of renewable energy sources, such as solar and wind, into existing energy grids. This involves addressing the variability and intermittency of renewable sources [109].
- Resource Allocation: Quantum algorithms can optimize the allocation of energy resources, including the scheduling of power generation from various sources to meet demand while considering factors like cost and environmental impact [110].
- Energy Storage Management: Quantum computing may enhance the optimization of energy storage systems by helping the determination of the optimal locations and capacities for energy storage facilities, as well as by delivering the most efficient use of stored energy [111].
- Smart Grids and Demand Response: Quantum algorithms can contribute to the development of smarter energy grids, enabling better demand–response mechanisms and the efficient utilization of energy resources based on real-time demand fluctuations [112].
- Carbon Emission Reduction: Quantum optimization can be applied to minimize carbon emissions by optimizing the energy mix, thus reducing reliance on fossil fuels and identifying cleaner energy alternatives [109].
- Supply Chain Optimization: Quantum computing can optimize the supply chain for energy-related components, thereby leading to improved efficiency in manufacturing, transportation, and maintenance processes [113].
- Exploration of New Materials: Quantum computers can aid in the exploration of new materials for energy storage and conversion, thus potentially accelerating the development of advanced energy technologies [114].
5.1. Quantum Technologies and Law Enforcement
5.2. Summary
6. Conclusions and Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Greenberger, D.; Hentschel, K.; Weinert, F. (Eds.) Compendium of Quantum Physics; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Planck, M. Ueber das Gesetz der Energieverteilung im Normalspectrum. Ann. Phys. 1901, 309, 553–563. [Google Scholar] [CrossRef]
- Bohr, N.I. On the constitution of atoms and molecules. Lond. Edinb. Dublin Philos. Mag. Sci. 1913, 26, 1–25. [Google Scholar] [CrossRef]
- Schrödinger, E. Quantisierung als Eigenwertproblem. Ann. Phys. 1926, 384, 361–376. [Google Scholar] [CrossRef]
- Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 1927, 43, 172–198. [Google Scholar] [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein Podolsky Rosen paradox. Phys. Phys. Fiz. 1964, 1, 195. [Google Scholar] [CrossRef]
- Dowling, J.P.; Milburn, G.J. Quantum technology: The second quantum revolution. Phil. Trans. R. Soc. A 2003, 361, 1655–1674. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H.; Bernstein, E.; Brassard, G.; Vazirani, U. Strengths and Weaknesses of Quantum Computing. SIAM J. Comput. 1997, 26, 1510–1523. [Google Scholar] [CrossRef]
- Jaeger, L. The Second Quantum Revolution: From Entanglement to Quantum Computing and Other Super-Technologies; Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Newton, I.; Cohen, I.; Schofield, R.; Hall, M. Isaac Newton’s Papers & Letters on Natural Philosophy and Related Documents; Harvard University Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Onofri, E.; Destri, C. Istituzioni di Fisica Teorica; Carocci: Rome, Italy, 1996. [Google Scholar]
- Friebe, C.; Brewer, W.; Kuhlmann, M.; Lyre, H.; Näger, P.; Passon, O.; Stöckler, M. The Philosophy of Quantum Physics; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Hance, J.R.; Ji, M.; Hofmann, H.F. Contextuality, coherences, and quantum Cheshire cats. New J. Phys. 2023, 25, 113028. [Google Scholar] [CrossRef]
- Deutsch, D. Comment on Lockwood. Br. J. Philos. Sci. 1996, 47, 222–228. [Google Scholar] [CrossRef]
- Norsen, T. Foundations of Quantum Mechanics: An Exploration of the Physical Meaning of Quantum Theory; Undergraduate Lecture Notes in Physics; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Casella, P.; Noce, C. Causality and no-go theorems. Sci. Philos. 2023, 11, 95–108. [Google Scholar] [CrossRef]
- Bohm, D.; Hiley, B.J.; Kaloyerou, P.N. An Ontological Basis for the Quantum Theory. 1. Nonrelativistic Particle Systems. 2. A Causal Interpretation of Quantum Fields. Phys. Rept. 1987, 144, 323–375. [Google Scholar] [CrossRef]
- Aspect, A.; Grangier, P.; Roger, G. Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A New Violation of Bell’s Inequalities. Phys. Rev. Lett. 1982, 49, 91–94. [Google Scholar] [CrossRef]
- Brassard, G. Profile of John Clauser, Alain Aspect and Anton Zeilinger: 2022 Nobel laureates in Physics. Proc. Natl. Acad. Sci. USA 2023, 120, e2304809120. [Google Scholar] [CrossRef] [PubMed]
- Wootters, W.K.; Zurek, W.H. Complementarity in the double-slit experiment: Quantum nonseparability and a quantitative statement of Bohr’s principle. Phys. Rev. D 1979, 19, 473–484. [Google Scholar] [CrossRef]
- Greenberger, D.M.; Yasin, A. Simultaneous wave and particle knowledge in a neutron interferometer. Phys. Lett. A 1988, 128, 391–394. [Google Scholar] [CrossRef]
- Qian, X.F.; Konthasinghe, K.; Manikandan, S.K.; Spiecker, D.; Vamivakas, A.N.; Eberly, J.H. Turning off quantum duality. Phys. Rev. Res. 2020, 2, 012016. [Google Scholar] [CrossRef]
- Qian, X.F.; Vamivakas, A.N.; Eberly, J.H. Entanglement limits duality and vice versa. Optica 2018, 5, 942–947. [Google Scholar] [CrossRef]
- Maleki, Y. Stereographic geometry of coherence and which-path information. Opt. Lett. 2019, 44, 5513. [Google Scholar] [CrossRef] [PubMed]
- Maleki, Y.; Suhail, Z.M. Revisiting wave–particle duality in Bohr–Einstein debate. AVS Quantum Sci. 2023, 5, 031401. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 1998, 80, 2245–2248. [Google Scholar] [CrossRef]
- Jakob, M.; Bergou, J.A. Quantitative complementarity relations in bipartite systems: Entanglement as a physical reality. Opt. Commun. 2010, 283, 827–830. [Google Scholar] [CrossRef]
- Qureshi, T. Predictability, distinguishability, and entanglement. Opt. Lett. 2021, 46, 492. [Google Scholar] [CrossRef] [PubMed]
- Truda, L.; Trotta, A.; Noce, C. Can the entanglement be considered a basic concept of quantum mechanics? Sci. Philos. 2022, 10, 57–69. [Google Scholar] [CrossRef]
- Various. Quantum Manifesto: A New Era of Technology. 2016. Available online: https://www.cineca.it/sites/default/files/temi-caldi/quantum_manifesto.pdf (accessed on 4 August 2023).
- Satanassi, S. The challenge of Quantum Manifesto for science education: Designing a teaching module on quantum computers for secondary school students. Il Nuovo C. 2020, 43, 1–11. [Google Scholar]
- Fox, M.F.J.; Zwickl, B.M.; Lewandowski, H.J. Preparing for the quantum revolution: What is the role of higher education? Phys. Rev. Phys. Educ. Res. 2020, 16, 020131. [Google Scholar] [CrossRef]
- Schrödinger, E. Discussion of probability relations between separated systems. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1935; Volume 31, pp. 555–563. [Google Scholar]
- Noce, C. Modern Physics: A Critical Approach; IOP Publishing: Bristol, UK, 2020. [Google Scholar]
- Coleman, S. Sidney Coleman’s Dirac Lecture ’Quantum Mechanics in Your Face’. arXiv 2020, arXiv:2011.12671. [Google Scholar]
- Ferraioli, A.G.; Noce, C. The measurement problem in quantum mechanics. Sci. Philos. 2019, 7, 41–58. [Google Scholar] [CrossRef]
- Castellani, L.G. Teletrasporto: Dalla Fantascienza alla Realtà; Springer: Cham, Switzerland, 2011. [Google Scholar]
- Bell, J. Dicibile e Indicibile in Meccanica Quantistica; Biblioteca Scientifica; Adelphi: Milan, Italy, 2010; Volume 45. [Google Scholar]
- Lebedev, A.V.; Blatter, G.B.L. Generating spin-entangled electron pairs in normal conductors using voltage pulses. Phys. Rev. B 2005, 72, 245314. [Google Scholar] [CrossRef]
- Aspect, A.; Grangier, G.R.P. Experimental Tests of Realistic Local Theories via Bell’s Theorem. Phys. Rev. Lett. 1981, 47, 460. [Google Scholar] [CrossRef]
- Weihs, G.; Jennewein, T.; Simon, C.; Weinfurter, H.; Zeilinger, A. Violation of Bell’s Inequality under Strict Einstein Locality Conditions. Phys. Rev. Lett. 1998, 81, 5039–5043. [Google Scholar] [CrossRef]
- Ozaydin, F.; Sarkar, R.; Bayrakci, V.; Bayındır, C.; Altintas, A.A.; Müstecaplıoglu, O.E. Engineering Four-Qubit Fuel States for Protecting Quantum Thermalization Machine from Decoherence. Information 2024, 15, 35. [Google Scholar] [CrossRef]
- Mermin, N.D. Bringing home the atomic world: Quantum mysteries for anybody. Am. J. Phys. 1981, 49, 940–943. [Google Scholar] [CrossRef]
- Bruce, C. The Strange Case of Mrs Hudson’s Cat: Or Sherlock Holmes Solves the Einstein Mysteries; Vintage: New York, NY, USA, 1998. [Google Scholar]
- Hossenfelder, S.; Palmer, T. Rethinking superdeterminism. Front. Phys. 2020, 8, 139. [Google Scholar] [CrossRef]
- Heisenberg, W. Physics and Beyond: Encounters and Conversations; Harper Torchbooks, Harper & Row: New York, NY, USA, 1971. [Google Scholar]
- Feynman, R.; Wilczek, F. The Character of Physical Law, with New Foreword; The MIT Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Marckwordt, J.; Muller, A.; Harlow, D.; Franklin, D.; Landsberg, R.H. Entanglement Ball: Using Dodgeball to Introduce Quantum Entanglement. Phys. Teach. 2021, 59, 613–616. [Google Scholar] [CrossRef]
- Ross, R. Computer simulation of Mermin’s quantum device. Am. J. Phys. 2020, 88, 483–489. [Google Scholar] [CrossRef]
- Atzori, M.; Sessoli, R. The Second Quantum Revolution: Role and Challenges of Molecular Chemistry. J. Am. Chem. Soc. 2019, 141, 11339–11352. [Google Scholar] [CrossRef] [PubMed]
- Kwon, S.; Tomonaga, A.; Lakshmi Bhai, G.; Devitt, S.J.; Tsai, J.S. Gate-based superconducting quantum computing. J. Appl. Phys. 2021, 129, 041102. [Google Scholar] [CrossRef]
- DiVincenzo, D.P. The Physical Implementation of Quantum Computation. Fortschritte Phys. 2000, 48, 771–783. [Google Scholar] [CrossRef]
- Knill, E.; Laflamme, R.; Milburn, G.J. A scheme for efficient quantum computation with linear optics. Nature 2001, 409, 46–52. [Google Scholar] [CrossRef] [PubMed]
- Hanson, R.; Awschalom, D.D. Coherent manipulation of single spins in semiconductors. Nature 2008, 453, 1043–1049. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Wu, D.; Fan, D.; Zhu, X. Superconducting quantum computing: A review. Sci. China Inf. Sci. 2020, 63, 180501. [Google Scholar] [CrossRef]
- van der Sar, T.; Wang, Z.H.; Blok, M.S.; Bernien, H.; Taminiau, T.H.; Toyli, D.M.; Lidar, D.A.; Awschalom, D.D.; Hanson, R.; Dobrovitski, V.V. Decoherence-protected quantum gates for a hybrid solid-state spin register. Nature 2012, 484, 82–86. [Google Scholar] [CrossRef] [PubMed]
- Pla, J.J.; Tan, K.Y.; Dehollain, J.P.; Lim, W.H.; Morton, J.J.L.; Jamieson, D.N.; Dzurak, A.S.; Morello, A. A single-atom electron spin qubit in silicon. Nature 2012, 489, 541–545. [Google Scholar] [CrossRef] [PubMed]
- Gatteschi, D.; Sessoli, R.; Villain, J. Molecular Nanomagnets; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Warren, W.S. The Usefulness of NMR Quantum Computing. Science 1997, 277, 1688–1690. [Google Scholar] [CrossRef]
- Jeschke, G.; Schweiger, A. Principles of Pulse Electron Paramagnetic Resonance; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Sessoli, R.; Gatteschi, D.; Caneschi, A.; Novak, M.A. Magnetic bistability in a metal-ion cluster. Nature 1993, 365, 141–143. [Google Scholar] [CrossRef]
- Eaton, S.S.; Eaton, G.R. Determination of Distances Based on T1 and Tm Effects. In Distance Measurements in Biological Systems by EPR; Berliner, L.J., Eaton, G.R., Eaton, S.S., Eds.; Springer US: Boston, MA, USA, 2000; pp. 347–381. [Google Scholar] [CrossRef]
- Bader, K.; Dengler, D.; Lenz, S.; Endeward, B.; Jiang, S.D.; Neugebauer, P.; van Slageren, J. Room temperature quantum coherence in a potential molecular qubit. Nat. Commun. 2014, 5, 5304. [Google Scholar] [CrossRef] [PubMed]
- Zadrozny, J.M.; Niklas, J.; Poluektov, O.G.; Freedman, D.E. Millisecond Coherence Time in a Tunable Molecular Electronic Spin Qubit. ACS Cent. Sci. 2015, 1, 488–492. [Google Scholar] [CrossRef] [PubMed]
- Abragam, A.; Goldman, M. Principles of dynamic nuclear polarisation. Rep. Prog. Phys. 1978, 41, 395. [Google Scholar] [CrossRef]
- Kane, B.E. A silicon-based nuclear spin quantum computer. Nature 1998, 393, 133–137. [Google Scholar] [CrossRef]
- Bernhardt, C. Quantum Computing for Everyone; MIT Press: Cambridge, MA, USA, 2019. [Google Scholar] [CrossRef]
- Aromí, G.; Aguilà, D.; Gamez, P.; Luis, F.; Roubeau, O. Design of magnetic coordination complexes for quantum computing. Chem. Soc. Rev. 2012, 41, 537–546. [Google Scholar] [CrossRef] [PubMed]
- Ferrando-Soria, J.; Moreno Pineda, E.; Chiesa, A.; Fernandez, A.; Magee, S.A.; Carretta, S.; Santini, P.; Vitorica-Yrezabal, I.J.; Tuna, F.; Timco, G.A.; et al. A modular design of molecular qubits to implement universal quantum gates. Nat. Commun. 2016, 7, 11377. [Google Scholar] [CrossRef] [PubMed]
- Atzori, M.; Chiesa, A.; Morra, E.; Chiesa, M.; Sorace, L.; Carretta, S.; Sessoli, R. A two-qubit molecular architecture for electron-mediated nuclear quantum simulation. Chem. Sci. 2018, 9, 6183–6192. [Google Scholar] [CrossRef] [PubMed]
- Ghirri, A.; Candini, A.; Affronte, M. Molecular Spins in the Context of Quantum Technologies. Magnetochemistry 2017, 3, 12. [Google Scholar] [CrossRef]
- Cleuziou, J.P.; Wernsdorfer, W.; Bouchiat, V.; Ondarçuhu, T.; Monthioux, M. Carbon nanotube superconducting quantum interference device. Nat. Nanotechnol. 2006, 1, 53–59. [Google Scholar] [CrossRef] [PubMed]
- Eaton, S.S.; Eaton, G.R. Relaxation Times of Organic Radicals and Transition Metal Ions. In Distance Measurements in Biological Systems by EPR; Berliner, L.J., Eaton, G.R., Eaton, S.S., Eds.; Springer US: Boston, MA, USA, 2000; pp. 29–154. [Google Scholar] [CrossRef]
- Candini, A.; Klyatskaya, S.; Ruben, M.; Wernsdorfer, W.; Affronte, M. Graphene Spintronic Devices with Molecular Nanomagnets. Nano Lett. 2011, 11, 2634–2639. [Google Scholar] [CrossRef] [PubMed]
- Urdampilleta, M.; Klyatskaya, S.; Cleuziou, J.P.; Ruben, M.; Wernsdorfer, W. Supramolecular spin valves. Nat. Mater. 2011, 10, 502–506. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary ed; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Moreno-Pineda, E.; Godfrin, C.; Balestro, F.; Wernsdorfer, W.; Ruben, M. Molecular spin qudits for quantum algorithms. Chem. Soc. Rev. 2018, 47, 501–513. [Google Scholar] [CrossRef] [PubMed]
- Hill, M.D. What is Scalability? In Scalable Shared Memory Multiprocessors; Dubois, M., Thakkar, S., Eds.; Springer US: Boston, MA, USA, 1992; pp. 89–96. [Google Scholar] [CrossRef]
- Bonizzoni, C.; Ghirri, A.; Atzori, M.; Sorace, L.; Sessoli, R.; Affronte, M. Coherent coupling between Vanadyl Phthalocyanine spin ensemble and microwave photons: Towards integration of molecular spin qubits into quantum circuits. Sci. Rep. 2017, 7, 13096. [Google Scholar] [CrossRef] [PubMed]
- Gimeno, I.; Kersten, W.; Pallarés, M.C.; Hermosilla, P.; Martínez-Pérez, M.J.; Jenkins, M.D.; Angerer, A.; Sánchez-Azqueta, C.; Zueco, D.; Majer, J.; et al. Enhanced Molecular Spin-Photon Coupling at Superconducting Nanoconstrictions. ACS Nano 2020, 14, 8707–8715. [Google Scholar] [CrossRef] [PubMed]
- Serrano, G.; Poggini, L.; Briganti, M.; Sorrentino, A.L.; Cucinotta, G.; Malavolti, L.; Cortigiani, B.; Otero, E.; Sainctavit, P.; Loth, S.; et al. Quantum dynamics of a single molecule magnet on superconducting Pb(111). Nat. Mater. 2020, 19, 546–551. [Google Scholar] [CrossRef] [PubMed]
- Prozorov, R.; Giannetta, R.W.; Polyanskii, A.A.; Perkins, G.K. Topological hysteresis in the intermediate state of type-I superconductors. Phys. Rev. B 2005, 72, 212508. [Google Scholar] [CrossRef]
- Thiele, S.; Vincent, R.; Holzmann, M.; Klyatskaya, S.; Ruben, M.; Balestro, F.; Wernsdorfer, W. Electrical Readout of Individual Nuclear Spin Trajectories in a Single-Molecule Magnet Spin Transistor. Phys. Rev. Lett. 2013, 111, 037203. [Google Scholar] [CrossRef] [PubMed]
- Vincent, R.; Klyatskaya, S.; Ruben, M.; Wernsdorfer, W.; Balestro, F. Electronic read-out of a single nuclear spin using a molecular spin transistor. Nature 2012, 488, 357–360. [Google Scholar] [CrossRef] [PubMed]
- Urdampilleta, M.; Klayatskaya, S.; Ruben, M.; Wernsdorfer, W. Magnetic Interaction Between a Radical Spin and a Single-Molecule Magnet in a Molecular Spin-Valve. ACS Nano 2015, 9, 4458–4464. [Google Scholar] [CrossRef] [PubMed]
- Bogani, L.; Wernsdorfer, W. Molecular spintronics using single-molecule magnets. Nat. Mater. 2008, 7, 179–186. [Google Scholar] [CrossRef] [PubMed]
- Thiele, S.; Balestro, F.; Ballou, R.; Klyatskaya, S.; Ruben, M.; Wernsdorfer, W. Electrically driven nuclear spin resonance in single-molecule magnets. Science 2014, 344, 1135–1138. [Google Scholar] [CrossRef] [PubMed]
- Grover, L.K. Quantum Mechanics Helps in Searching for a Needle in a Haystack. Phys. Rev. Lett. 1997, 79, 325–328. [Google Scholar] [CrossRef]
- Ruan, L.; Tong, J.; Luo, F.; Wu, Y.; Qin, G.; Jiao, X.; Zhang, X. The magnetic anisotropy of Tb-phthalocyanine films effected by molecular orientation. Appl. Surf. Sci. 2022, 585, 152445. [Google Scholar] [CrossRef]
- Mannini, M.; Bertani, F.; Tudisco, C.; Malavolti, L.; Poggini, L.; Misztal, K.; Menozzi, D.; Motta, A.; Otero, E.; Ohresser, P.; et al. Magnetic behaviour of TbPc2 single-molecule magnets chemically grafted on silicon surface. Nat. Commun. 2014, 5, 4582. [Google Scholar] [CrossRef] [PubMed]
- Malavolti, L.; Mannini, M.; Car, P.E.; Campo, G.; Pineider, F.; Sessoli, R. Erratic magnetic hysteresis of TbPc2 molecular nanomagnets. J. Mater. Chem. C 2013, 1, 2935–2942. [Google Scholar] [CrossRef]
- Wäckerlin, C.; Donati, F.; Singha, A.; Baltic, R.; Rusponi, S.; Diller, K.; Patthey, F.; Pivetta, M.; Lan, Y.; Klyatskaya, S.; et al. Giant Hysteresis of Single-Molecule Magnets Adsorbed on a Nonmagnetic Insulator. Adv. Mater. 2016, 28, 5195–5199. [Google Scholar] [CrossRef] [PubMed]
- Malavolti, L.; Poggini, L.; Margheriti, L.; Chiappe, D.; Graziosi, P.; Cortigiani, B.; Lanzilotto, V.; de Mongeot, F.B.; Ohresser, P.; Otero, E.; et al. Magnetism of TbPc2 SMMs on ferromagnetic electrodes used in organic spintronics. Chem. Commun. 2013, 49, 11506–11508. [Google Scholar] [CrossRef] [PubMed]
- Studniarek, M.; Wäckerlin, C.; Singha, A.; Baltic, R.; Diller, K.; Donati, F.; Rusponi, S.; Brune, H.; Lan, Y.; Klyatskaya, S.; et al. Understanding the Superior Stability of Single-Molecule Magnets on an Oxide Film. Adv. Sci. 2019, 6, 1901736. [Google Scholar] [CrossRef] [PubMed]
- Serrano, G.; Poggini, L.; Cucinotta, G.; Sorrentino, A.L.; Giaconi, N.; Cortigiani, B.; Longo, D.; Otero, E.; Sainctavit, P.; Caneschi, A.; et al. Magnetic molecules as local sensors of topological hysteresis of superconductors. Nat. Commun. 2022, 13, 3838. [Google Scholar] [CrossRef] [PubMed]
- Fortini, A.; Paumier, E. Thermodynamics of metastable processes in the magnetization of type-I superconductors. Phys. Rev. B 1976, 14, 55–60. [Google Scholar] [CrossRef]
- Quantum Technology Monitor; McKinsey & Company: Chicago, IL, USA, 2023.
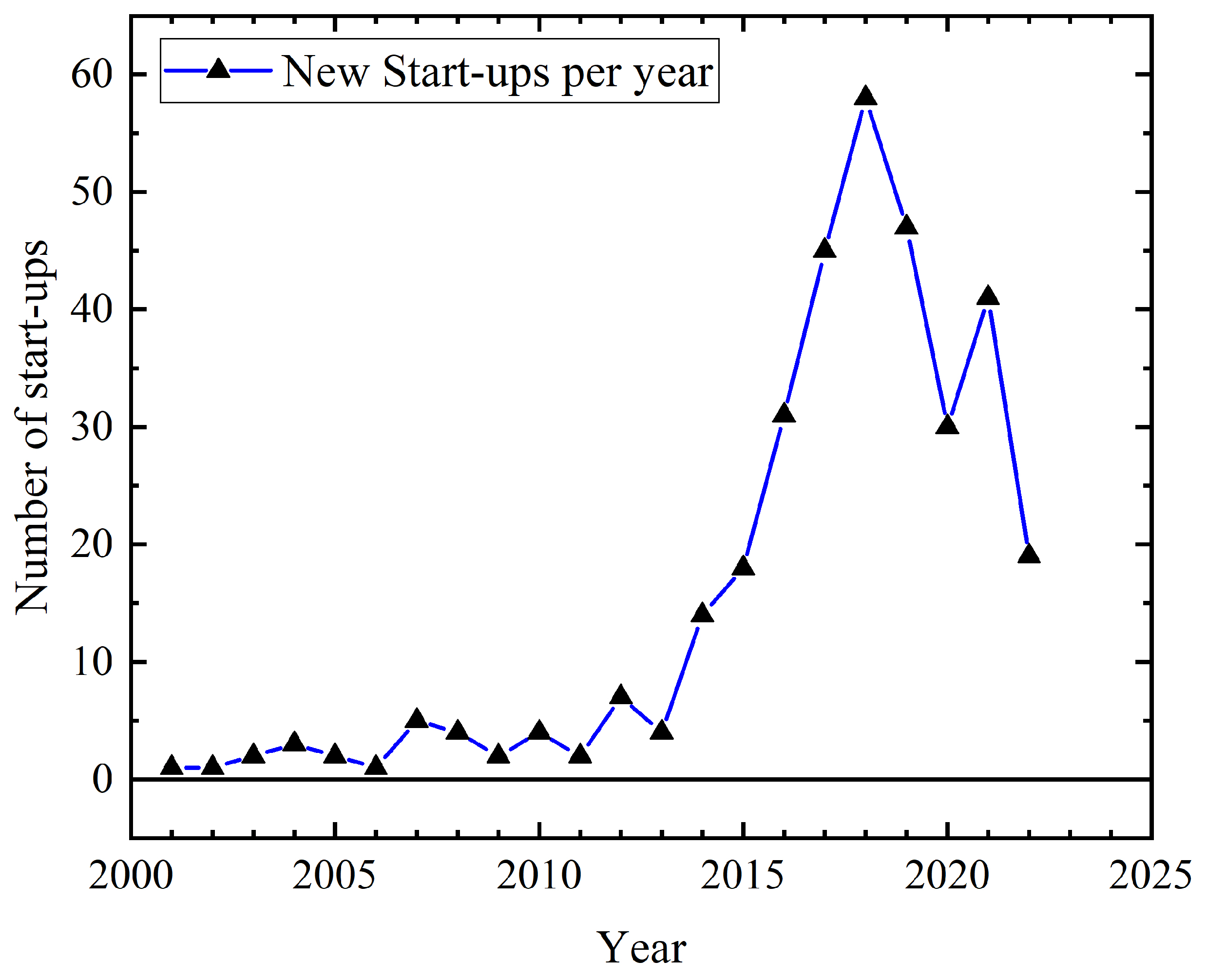
- Gibney, E. Quantum Gold Rush: The private funding pouring into quantum start-ups. Nature News, 2 October 2019. [Google Scholar]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [PubMed]
- Bova, F.; Goldfarb, A.; Melko, R.G. Commercial applications of quantum computing. epj Quantum Technol. 2021, 8, 2. [Google Scholar] [CrossRef] [PubMed]
- Bernstein, D.; Buchmann, J.; Dahmen, E. Post-Quantum Cryptography; Springer: Cham, Switzerland, 2010. [Google Scholar]
- Adams, P.H. Why Quantum Computing Could Make Today’s Cybersecurity Obsolete. 2019. Available online: https://www.weforum.org/agenda/2019/07/why-quantum-computing-could-make-todays-cybersecurity-obsolete/ (accessed on 10 February 2024).
- Blunt, N.S.; Camps, J.; Crawford, O.; Izsák, R.; Leontica, S.; Mirani, A.; Moylett, A.E.; Scivier, S.A.; Sünderhauf, C.; Schopf, P.; et al. Perspective on the current state-of-the-art of quantum computing for Drug Discovery Applications. J. Chem. Theory Comput. 2022, 18, 7001–7023. [Google Scholar] [CrossRef] [PubMed]
- Rosenberg, G.; Haghnegahdar, P.; Goddard, P.; Carr, P.; Wu, K.; de Prado, M.L. Solving the optimal trading trajectory problem using a quantum annealer. IEEE J. Sel. Top. Signal Process. 2016, 10, 1053–1060. [Google Scholar] [CrossRef]
- Orús, R.; Mugel, S.; Lizaso, E. Quantum computing for finance: Overview and prospects. Rev. Phys. 2019, 4, 100028. [Google Scholar] [CrossRef]
- Harwood, S.; Gambella, C.; Trenev, D.; Simonetto, A.; Bernal Neira, D.; Greenberg, D. Formulating and solving routing problems on quantum computers. IEEE Trans. Quantum Eng. 2021, 2, 3100118. [Google Scholar] [CrossRef]
- Ajagekar, A.; You, F. Quantum computing for energy systems optimization: Challenges and opportunities. Energy 2019, 179, 76–89. [Google Scholar] [CrossRef]
- Cooper, P.; Ernst, P.; Kiewell, D.; Pinner, D. Quantum Computing for Energy System Optimisation. 2022. Available online: https://qtft.org/post/quantum-computing-for-energy-system-optimisation (accessed on 10 February 2024).
- Giani, A.; Eldredge, Z. Quantum Computing Opportunities in Renewable Energy. SN Comput. Sci. 2021, 2, 393. [Google Scholar] [CrossRef]
- Raghav, L.P.; Kumar, R.S.; Raju, D.K.; Singh, A.R. Optimal Energy Management of Microgrids Using Quantum Teaching Learning Based Algorithm. IEEE Trans. Smart Grid 2021, 12, 4834–4842. [Google Scholar] [CrossRef]
- Mastroianni, C.; Plastina, F.; Scarcello, L.; Settino, J.; Vinci, A. Assessing Quantum Computing Performance for Energy Optimization in a Prosumer Community. IEEE Trans. Smart Grid 2024, 15, 444–456. [Google Scholar] [CrossRef]
- Jiang, H.; Shen, Z.M.; Liu, J. Quantum Computing Methods for Supply Chain Management. In Proceedings of the 2022 IEEE/ACM 7th Symposium on Edge Computing (SEC), Seattle, WA, USA, 5–8 December 2022; pp. 400–405. [Google Scholar] [CrossRef]
- Ho, A.; McClean, J.; Ong, S.P. The Promise and Challenges of Quantum Computing for Energy Storage. Joule 2018, 2, 810–813. [Google Scholar] [CrossRef]
- Langione, M.; Tillemann-Dick, C.; Kumar, A.; Taneja, V. Where will quantum computers create value-and when? BCG Global, 13 May 2019. [Google Scholar]
- The Second Quantum Revolution: The Impact of Quantum Computing and Quantum Technologies on Law Enforcement. 2023. Available online: https://www.europol.europa.eu/publication-events/main-reports/second-quantum-revolution-impact-of-quantum-computing-and-quantum-technologies-law-enforcement (accessed on 10 February 2024).
- Bernstein, D.J.; Buchmann, J.; Dahmen, E. Introduction to post-quantum cryptography. In Post-Quantum Cryptography; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–14. [Google Scholar] [CrossRef]
- Rodríguez, A.G. A Quantum Cybersecurity Agenda for Europe. 2023. Available online: https://www.epc.eu/en/publications/A-quantum-cybersecurity-agenda-for-Europe~526b9c (accessed on 10 February 2024).
- Lewis, A.; Ferigato, C.; Travagnin, M.; Florescu, E. The Impact of Quantum Technologies on the EU‘s Future Policies: Part 3 Perspectives for Quantum Computing. 2018. Available online: https://op.europa.eu/en/publication-detail/-/publication/35c653dc-e952-11e8-b690-01aa75ed71a1/language-en (accessed on 10 February 2024). [CrossRef]
- Richmond, K. AI, Machine Learning, and International Criminal Investigations: The Lessons From Forensic Science. iCourts Work. Pap. Ser. 2020, 222, 1–23. [Google Scholar] [CrossRef]
- Wittel, P. Quantum Machine Learning; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar] [CrossRef]
- Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum machine learning. Nature 2017, 549, 195–202. [Google Scholar] [CrossRef] [PubMed]
- Rebentrost, P.; Mohseni, M.; Lloyd, S. Quantum Support Vector Machine for Big Data Classification. Phys. Rev. Lett. 2014, 113, 130503. [Google Scholar] [CrossRef] [PubMed]
- Hoofnagle, C.J.; Garfinkel, S. Quantum Sensors—Unlike Quantum Computers—Are Already Here. 2022. Available online: https://www.defenseone.com/ideas/2022/06/quantum-sensorsunlike-quantum-computersare-already-here/368634/ (accessed on 10 February 2024).
- Sandeep, K.S.; Mazhar, K. The Role of Quantum Computing in Software Forensics and Digital Evidence: Issues and Challenges. In Limitations and Future Applications of Quantum Cryptography; IGI Global: Hershey, PA, USA, 2021; pp. 169–185. [Google Scholar] [CrossRef]
- Ganesan, M.; Nagaraaj, P. Quantum dots as nanosensors for detection of toxics: A literature review. Anal. Methods 2020, 12, 4254–4275. [Google Scholar] [CrossRef] [PubMed]
- Jeutner, V. The Quantum Imperative: Addressing the Legal Dimension of Quantum Computers. Morals Mach. 2021, 1, 52–59. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dušek, M.; Lütkenhaus, N.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301–1350. [Google Scholar] [CrossRef]
- Dürmuth, M.; Golla, M.; Markert, P.; May, A.; Schlieper, L. Towards Quantum Large-Scale Password Guessing on Real-World Distributions. Cryptology ePrint Archive, Paper 2021/1299. 2021. Available online: https://eprint.iacr.org/2021/1299 (accessed on 10 February 2024).
- Giovannetti, V.; Lloyd, S.; Maccone, L. Advances in quantum metrology. Nat. Photonics 2011, 5, 222–229. [Google Scholar] [CrossRef]
- Costanzo, H.; Gooch, J.; Frascione, N. Nanomaterials for optical biosensors in forensic analysis. Talanta 2023, 253, 123945. [Google Scholar] [CrossRef] [PubMed]
- Devitt, S.J.; Munro, W.J.; Nemoto, K. Quantum error correction for beginners. Rep. Prog. Phys. 2013, 76, 076001. [Google Scholar] [CrossRef] [PubMed]
- Boixo, S.; Isakov, S.V.; Smelyanskiy, V.N.; Babbush, R.; Ding, N.; Jiang, Z.; Bremner, M.J.; Martinis, J.M.; Neven, H. Characterizing quantum supremacy in near-term devices. Nat. Phys. 2018, 14, 595–600. [Google Scholar] [CrossRef]
- McAfee, A.; Brynjolfsson, E. Machine Platform Crowd: Harnessing Our Digital Future; W. W. Norton & Company: New York, NY, USA, 2018. [Google Scholar]

| Coin 1 | Coin 2 |
|---|---|
| First Die | Second Die |
|---|---|
| ❶❷❸❹❺❻ = | ❶❷❸❹❺❻ = |
| Subsystem 1 | Subsystem 2 |
|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Intonti, K.; Viscardi, L.; Lamberti, V.; Matteucci, A.; Micciola, B.; Modestino, M.; Noce, C. The Second Quantum Revolution: Unexplored Facts and Latest News. Encyclopedia 2024, 4, 630-671. https://doi.org/10.3390/encyclopedia4020040
Intonti K, Viscardi L, Lamberti V, Matteucci A, Micciola B, Modestino M, Noce C. The Second Quantum Revolution: Unexplored Facts and Latest News. Encyclopedia. 2024; 4(2):630-671. https://doi.org/10.3390/encyclopedia4020040
Chicago/Turabian StyleIntonti, Kimberly, Loredana Viscardi, Veruska Lamberti, Amedeo Matteucci, Bruno Micciola, Michele Modestino, and Canio Noce. 2024. "The Second Quantum Revolution: Unexplored Facts and Latest News" Encyclopedia 4, no. 2: 630-671. https://doi.org/10.3390/encyclopedia4020040
APA StyleIntonti, K., Viscardi, L., Lamberti, V., Matteucci, A., Micciola, B., Modestino, M., & Noce, C. (2024). The Second Quantum Revolution: Unexplored Facts and Latest News. Encyclopedia, 4(2), 630-671. https://doi.org/10.3390/encyclopedia4020040