The Oxidative Process of Acarbose, Maysin, and Luteolin with Maltase-Glucoamylase: Molecular Docking and Molecular Dynamics Study
Abstract
:1. Introduction
- (1)
- DFT calculations, which provide useful information about the chemical reactivity of the molecules and the most suitable areas for nucleophilic and electrophilic attacks;
- (2)
- Molinspiration Cheminformatics for the calculations of the polar surface area and the octanol-water partition coefficient (logP) values;
- (3)
- Molecular docking calculations, which determine the most favorable position of interaction between a ligand and a macromolecule by the binding energy;
- (4)
- Molecular dynamics calculations, for measuring the stability of the binding between these molecules, considering several contributions such as solvents, electrostatic energy, and temperature.
2. Computational Details
2.1. Quantum-Chemical Calculations
2.2. Molecular Docking Calculations
2.3. Molecular Dynamics
2.4. Binding Free Energy Calculations
3. Results and Discussion
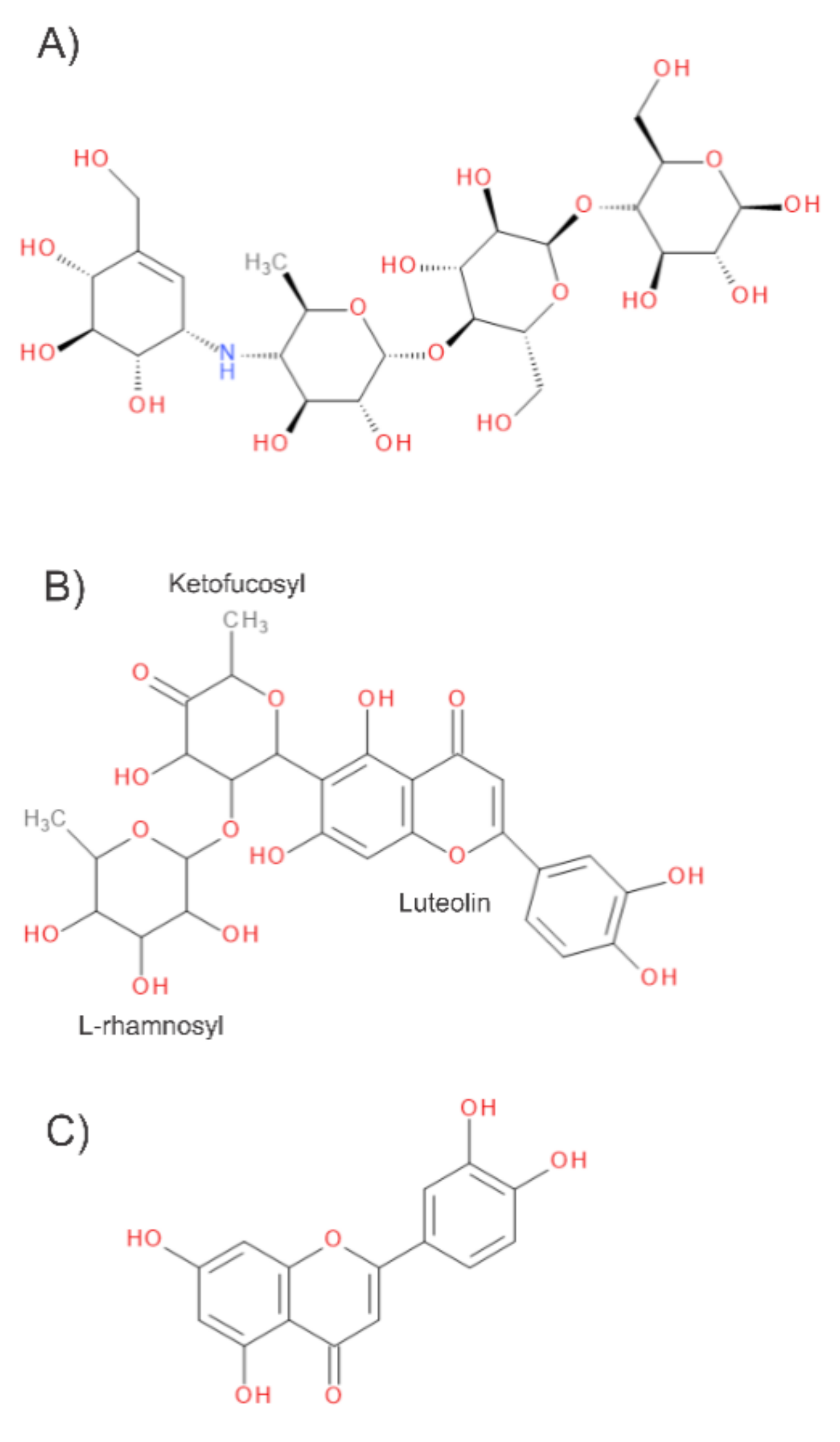
3.1. Geometry Optimization
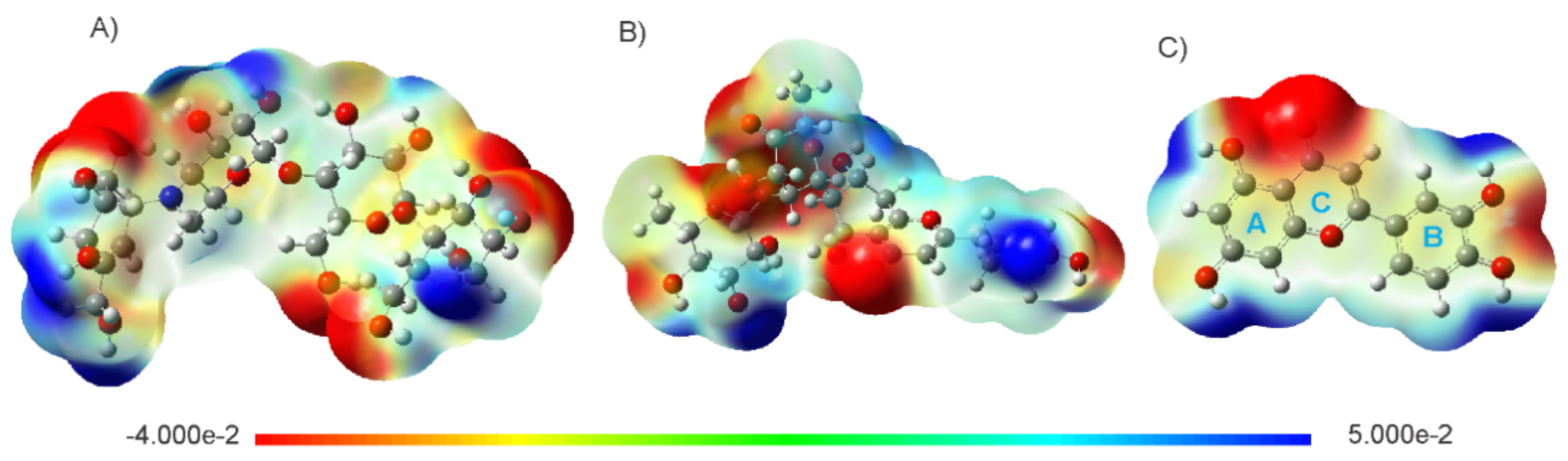
3.2. Frontier Molecular Orbitals and Electrostatic Potential Surface (EPS)
3.3. Polar Surface Area (PSA) and LogP
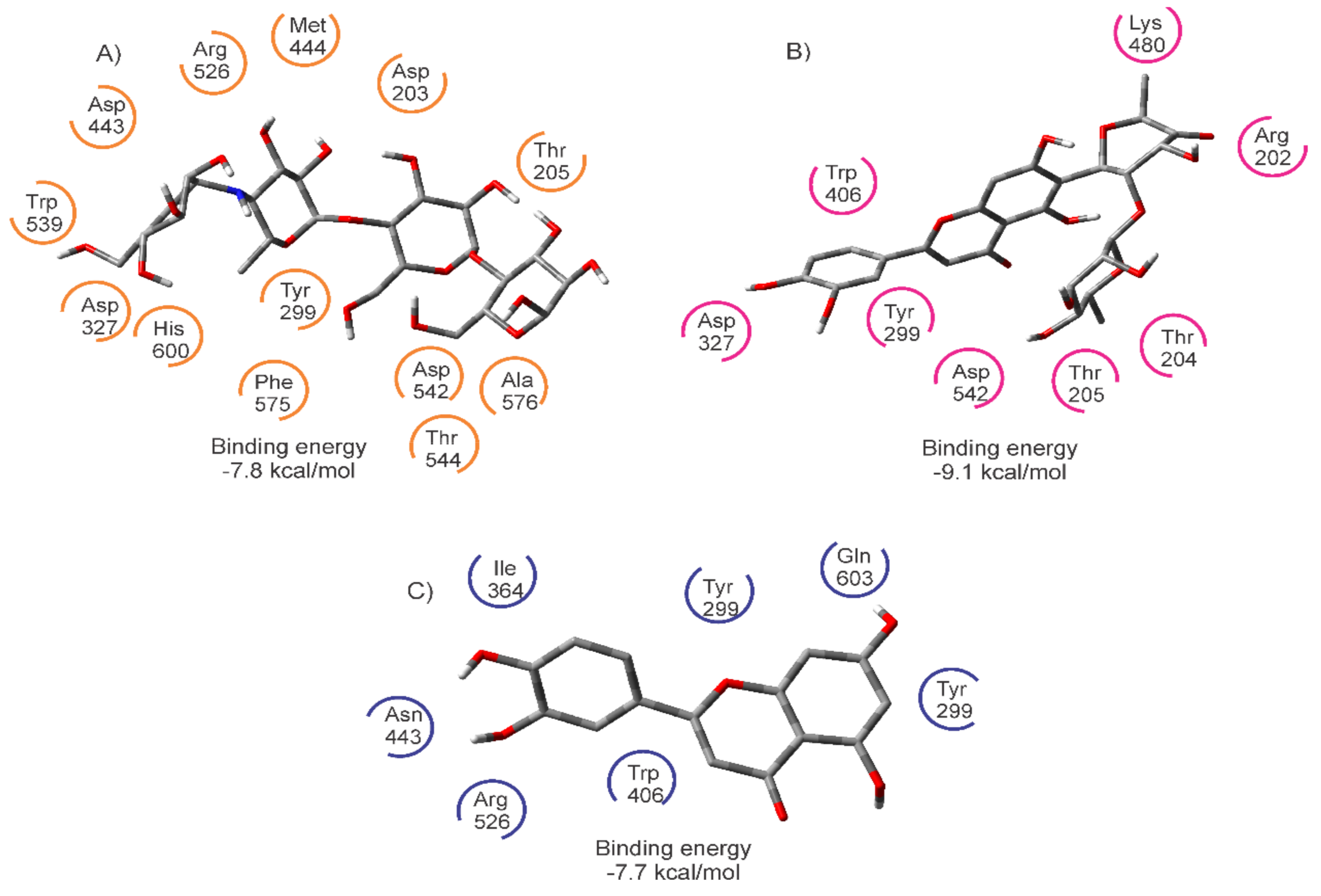
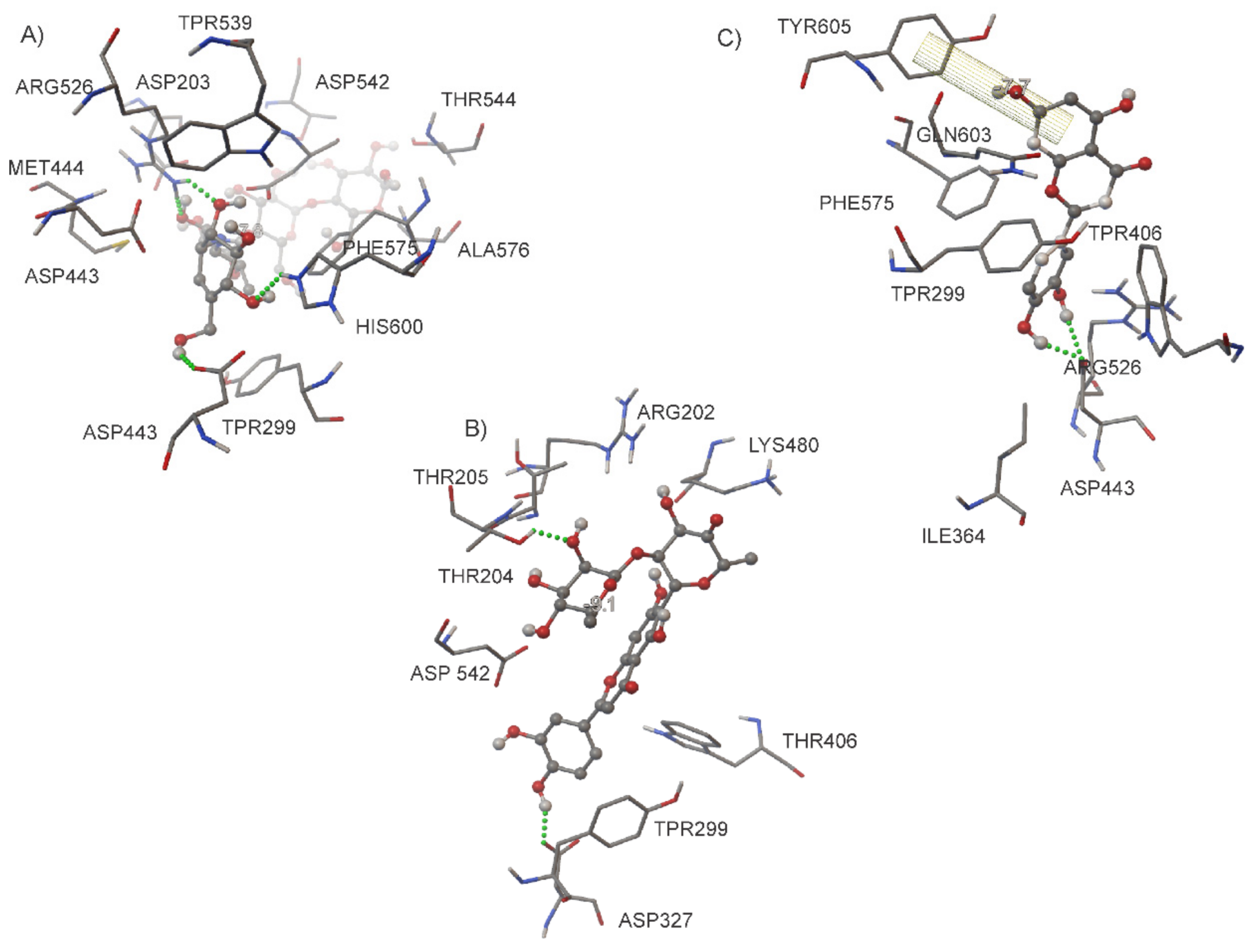
3.4. Molecular Docking Analysis between Ligands (ACA, MAY, and LUT) with Maltase-Glucoamylase (MGA)
3.5. Chemical Reactivity Parameters and Charge Transfer Descriptor
3.6. Molecular Dynamics Simulation Analysis
3.7. Binding Free Energy Calculation
- (1)
- Solvent contribution is the sum of electrostatic solvation energy (polar contribution or PB) and non-electrostatic solvation component (non-polar contribution SA);
- (2)
- Gas-phase contribution is the sum of electrostatic (elec) and Van der Waals interaction energies (vdW).
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Neel, J.V. Diabetes mellitus: A “thrifty” genotype rendered detrimental by “progress”? Am. J. Hum. Genet. 1962, 14, 353–362. [Google Scholar] [PubMed]
- Van De Laar, F.A. Alpha-glucosidase inhibitors in the early treatment of type 2 diabetes. Vasc. Health Risk Manag. 2008, 4, 1189–1195. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, A.H.-M.; Lee, B.-H.; Chang, W.-J. Small intestine mucosal α-glucosidase: A missing feature of in vitro starch digestibility. Food Hydrocoll. 2016, 53, 163–171. [Google Scholar] [CrossRef]
- Nair, S.S.; Kavrekar, V.; Mishra, A. In vitro studies on alpha amylase and alpha glucosidase inhibitory activities of selected plant extracts. Eur. J. Exp. Biol. 2013, 3, 128–132. [Google Scholar]
- Chiasson, J.-L.; Josse, R.G.; Gomis, R.; Hanefeld, M.; Karasik, A.; Laakso, M. Acarbose for prevention of type 2 diabetes mellitus: The STOP-NIDDM randomised trial. Lancet 2002, 359, 2072–2077. [Google Scholar] [CrossRef]
- Chahal, H. Comparative Review of Oral Hypoglycemic Agents in Adults; World Health Organization, 19th Expert Committee on the Selection and Use of Essential Medicines; World Health Organization: Geneva, Switzerland, 2013; Volume 18, pp. 1–37. [Google Scholar]
- Kim, S.L.; Jung, T.W. Maysin and other flavonoid contents in corn silks. Korean J. Breed 2001, 33, 338–343. [Google Scholar]
- Ando, C.; Takahashi, N.; Hirai, S.; Nishimura, K.; Lin, S.; Uemura, T.; Goto, T.; Yu, R.; Nakagami, J.; Murakami, S.; et al. Luteolin, a food-derived flavonoid, suppresses adipocyte-dependent activation of macrophages by inhibiting JNK activation. FEBS Lett. 2009, 583, 3649–3654. [Google Scholar] [CrossRef] [Green Version]
- Matsui, T.; Kobayashi, M.; Hayashida, S.; Matsumoto, K. Luteolin, a Flavone, Does Not Suppress Postprandial Glucose Absorption through an Inhibition of α-Glucosidase Action. Biosci. Biotechnol. Biochem. 2002, 66, 689–692. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, G.; Pan, J.; Wang, Y. α-Glucosidase inhibition by luteolin: Kinetics, interaction and molecular docking. Int. J. Biol. Macromol. 2014, 64, 213–223. [Google Scholar] [CrossRef]
- Zhang, B.-W.; Li, X.; Sun, W.-L.; Xing, Y.; Xiu, Z.-L.; Zhuang, C.-L.; Dong, Y.-S. Dietary Flavonoids and Acarbose Synergistically Inhibit α-Glucosidase and Lower Postprandial Blood Glucose. J. Agric. Food Chem. 2017, 65, 8319–8330. [Google Scholar] [CrossRef]
- Tadera, K.; Minami, Y.; Takamatsu, K.; Matsuoka, T. Inhibition of α-glucosidase and α-amylase by flavonoids. J. Nutr. Sci. Vitaminol. 2006, 52, 149–153. [Google Scholar] [CrossRef] [Green Version]
- Jia, Y.; Gao, X.; Xue, Z.; Wang, Y.; Lu, Y.; Zhang, M.; Panichayupakaranant, P.; Chen, H. Characterization, antioxidant activities, and inhibition on α-glucosidase activity of corn silk polysaccharides obtained by different extraction methods. Int. J. Biol. Macromol. 2020, 163, 1640–1648. [Google Scholar] [CrossRef]
- Alvarado-Díaz, C.S.; Gutiérrez-Méndez, N.; Mendoza-López, M.L.; Rodríguez-Rodríguez, M.Z.; Quintero-Ramos, A.; Landeros-Martínez, L.L.; Rodríguez-Valdez, L.M.; Rodríguez-Figueroa, J.C.; Pérez-Vega, S.; Salmeron-Ochoa, I.; et al. Inhibitory effect of saccharides and phenolic compounds from maize silks on intestinal α-glucosidases. J. Food Biochem. 2019, 43, e12896. [Google Scholar] [CrossRef]
- Remko, M. Theoretical study of molecular structure, pKa, lipophilicity, solubility, absorption, and polar surface area of some hypoglycemic agents. J. Mol. Struct. THEOCHEM 2009, 897, 73–82. [Google Scholar] [CrossRef]
- Flores-Holguin, N.; Landeros-Martinez, D.G.-M.L.-L.; Orrantia-Borunda, N.F.-H.E. Theoretical Calculation of UV-Vis, IR Spectra and Reactivity Properties of Tamoxifen Drug: A Methodology Comparison. MOJ Bioorganic Org. Chem. 2017, 1, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Landeros-Martinez, E.O.-B.L.-L.; Borunda, E.O. DFT Chemical Reactivity Analysis of Biological Molecules in the Presence of Silver Ion. Org. Chem. Curr. Res. 2016, 4, 1–6. [Google Scholar] [CrossRef]
- Maltarollo, V.G.; Homem-De-Mello, P.; Honório, K.M. Theoretical study on the molecular and electronic properties of some substances used for diabetes mellitus treatment. J. Mol. Model. 2009, 16, 799–804. [Google Scholar] [CrossRef]
- De Benedetti, P.G.; Quartieri, S.; Rastelli, A. A theoretical study of the structure-activity relationship in sulpha drugs. J. Mol. Struct. THEOCHEM 1981, 85, 45–51. [Google Scholar] [CrossRef]
- Luzhkov, V. Electronic parameters and molecular mechanisms of biological action of nitroxyl radicals. J. Mol. Struct. THEOCHEM 1985, 121, 165–172. [Google Scholar] [CrossRef]
- Rao, Y.S.; Prasad, M.; Sri, N.U.; Veeraiah, V. Vibrational (FT-IR, FT-Raman) and UV–Visible spectroscopic studies, HOMO–LUMO, NBO, NLO and MEP analysis of Benzyl (imino (1H-pyrazol-1-yl) methyl) carbamate using DFT calculaions. J. Mol. Struct. 2016, 1108, 567–582. [Google Scholar] [CrossRef]
- Trott, O.; Olson, A.J. AutoDock Vina: Improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J. Comput. Chem. 2010, 31, 455–461. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bultinck, P.; De Winter, H.; Langenaeker, W.; Tollenare, J.P. Computational Medicinal Chemistry for Drug Discovery; Apple Academic Press: Palm Bay, FL, USA, 2003; ISBN 0203913396. [Google Scholar] [CrossRef] [Green Version]
- Kitchen, D.B.; Decornez, H.; Furr, J.R.; Bajorath, J. Docking and scoring in virtual screening for drug discovery: Methods and applications. Nat. Rev. Drug Discov. 2004, 3, 935–949. [Google Scholar] [CrossRef] [PubMed]
- Przylas, I.; Terada, Y.; Fujii, K.; Takaha, T.; Saenger, W.; Sträter, N. X-ray structure of acarbose bound to amylomaltase from Thermus aquaticus. JBIC J. Biol. Inorg. Chem. 2000, 267, 6903–6913. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, L.-L.; Han, J.; Ran, J.-X.; Chen, X.-P.; Wang, Z.-H.; Wu, F.-H. 3D-QSAR, molecular docking and molecular dynamics simulations of oxazepane amidoacetonitrile derivatives as novel DPPI inhibitors. J. Mol. Struct. 2018, 1168, 223–233. [Google Scholar] [CrossRef]
- Safarizadeh, H.; Garkani-Nejad, Z. Investigation of MI-2 analogues as MALT1 inhibitors to treat of diffuse large B-Cell lymphoma through combined molecular dynamics simulation, molecular docking and QSAR techniques and design of new inhibitors. J. Mol. Struct. 2019, 1180, 708–722. [Google Scholar] [CrossRef]
- Wang, Z.-Z.; Ma, C.-Y.; Yang, J.; Gao, Q.-B.; Sun, X.-D.; Ding, L.; Liu, H.-M. Investigating the binding mechanism of (4-Cyanophenyl)glycine derivatives as reversible LSD1 by 3D-QSAR, molecular docking and molecular dynamics simulations. J. Mol. Struct. 2019, 1175, 698–707. [Google Scholar] [CrossRef]
- Naseem, S.; Khalid, M.; Tahir, M.N.; Halim, M.A.; Braga, A.A.; Naseer, M.M.; Shafiq, Z. Synthesis, structural, DFT studies, docking and antibacterial activity of a xanthene based hydrazone ligand. J. Mol. Struct. 2017, 1143, 235–244. [Google Scholar] [CrossRef]
- Barakat, A.; Islam, M.S.; Al-Majid, A.M.; Soliman, S.M.; Ghabbour, H.A.; Yousuf, S.; Choudhary, M.I.; Ul-Haq, Z. Synthesis, molecular structure, spectral analysis, and biological activity of new malonamide derivatives as α-glucosidase inhibitors. J. Mol. Struct. 2017, 1134, 253–264. [Google Scholar] [CrossRef]
- Jhong, C.-H.; Riyaphan, J.; Lin, S.-H.; Chia, Y.-C.; Weng, C.-F. Screening alpha-glucosidase and alpha-amylase inhibitors from natural compounds by molecular dockingin silico. BioFactors 2015, 41, 242–251. [Google Scholar] [CrossRef]
- Saqib, U.; Siddiqi, M.I. Probing ligand binding interactions of human alpha glucosidase by homology modeling and molecular docking. Intern. J. Integr. Biol. 2008, 2, 116–121. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. Density Functionals with Broad Applicability in Chemistry. Acc. Chem. Res. 2008, 41, 157–167. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef] [Green Version]
- Curtiss, L.A.; Raghavachari, K.; Redfern, P.C.; Rassolov, V.A.; Pople, J.A. Gaussian-3 (G3) theory for molecules containing first and second-row atoms. J. Chem. Phys. 1998, 109, 7764–7776. [Google Scholar] [CrossRef]
- Tomasi, J.; Persico, M. Molecular Interactions in Solution: An Overview of Methods Based on Continuous Distributions of the Solvent. Chem. Rev. 1994, 94, 2027–2094. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Hirshfeld, F.L. Bonded-atom fragments for describing molecular charge densities. Theor. Chem. Acc. 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Foresman, J.B.; Frisch, A.E. Exploring Chemistry with Electronic Structure Methods; Gaussian, Inc.: Pittsburgh, PA, USA, 1996. [Google Scholar]
- Lewars, E.G. Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics; Springer Science & Business Media: New York, NY, USA, 2010; ISBN 9048138620. [Google Scholar]
- Parr, R.G.; Pearson, R.G. Absolute hardness: Companion parameter to absolute electronegativity. J. Am. Chem. Soc. 1983, 105, 7512–7516. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W. Density functional approach to the frontier-electron theory of chemical reactivity. J. Am. Chem. Soc. 1984, 106, 4049–4050. [Google Scholar] [CrossRef]
- Parr, R.G.; Szentpály, L.V.; Liu, S. Electrophilicity Index. J. Am. Chem. Soc. 1999, 121, 1922–1924. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W. Density Functional Theory of Atoms and Molecules, 1st ed.; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Wang, X.; Song, L.; Tian, C.; He, J.; Wang, S.; Wang, J.; Li, C. DFT Investigation of the Effects of Coexisting Cations and Complexing Reagents on Ni(II) Adsorption by a Polyvinylidene Fluoride-Type Chelating Membrane Bearing Poly(Amino Phosphonic Acid) Groups. Metals 2017, 7, 61. [Google Scholar] [CrossRef] [Green Version]
- Padmanabhan, J.; Parthasarathi, R.; Subramanian, V.; Chattaraj, P.K. Electrophilicity-Based Charge Transfer Descriptor. J. Phys. Chem. A 2007, 111, 1358–1361. [Google Scholar] [CrossRef] [PubMed]
- Molinspiration Molinspiration-Chemoinformatics on the Web. Available online: http://www.molinspiration.com/ (accessed on 28 April 2021).
- Weininger, D. Smiles, a chemical language and information system. 1. Introduction to methodology and encoding rules. J. Chem. Inf. Model. 1988, 28, 31–36. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2009, 31, 671–690. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kalé, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [Green Version]
- Šali, A.; Blundell, T.L. Comparative Protein Modelling by Satisfaction of Spatial Restraints. J. Mol. Biol. 1993, 234, 779–815. [Google Scholar] [CrossRef]
- Da Silva, A.W.S.; Vranken, W.F. ACPYPE-AnteChamber PYthon Parser interfacE. BMC Res. Notes 2012, 5, 367. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Wang, W.; Kollman, P.A.; Case, D.A. Antechamber: An accessory software package for molecular mechanical calculations. J. Am. Chem. Soc. 2001, 222, U403. [Google Scholar]
- Case, D.A.; Ben-Shalom, I.Y.; Brozell, S.R.; Cerutti, D.S.; Cheatham, T.E., III; Cruzeiro, V.W.D.; Darden, T.A.; Duke, R.E.; Ghoreishi, D.; Gilson, M.K. AMBER 2018; University of California: San Francisco, CA, USA, 2018. [Google Scholar]
- Elstner, M.; Porezag, D.; Jungnickel, G.; Elsner, J.; Haugk, M.; Frauenheim, T.; Suhai, S.; Seifert, G. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260–7268. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Martyna, G.J.; Tobias, D.J.; Klein, M.L. Constant pressure molecular dynamics algorithms. J. Chem. Phys. 1994, 101, 4177–4189. [Google Scholar] [CrossRef]
- Feller, S.E.; Zhang, Y.; Pastor, R.W.; Brooks, B.R. Constant pressure molecular dynamics simulation: The Langevin piston method. J. Chem. Phys. 1995, 103, 4613–4621. [Google Scholar] [CrossRef]
- Deniz, U.; Ozkirimli, E.; Ulgen, K.O. A systematic methodology for large scale compound screening: A case study on the discovery of novel S1PL inhibitors. J. Mol. Graph. Model. 2016, 63, 110–124. [Google Scholar] [CrossRef] [PubMed]
- Baker, N.A.; Sept, D.; Joseph, S.; Holst, M.J.; McCammon, J.A. Electrostatics of nanosystems: Application to microtubules and the ribosome. Proc. Natl. Acad. Sci. USA 2001, 98, 10037–10041. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hou, T.; Wang, J.; Li, Y.; Wang, W. Assessing the Performance of the MM/PBSA and MM/GBSA Methods. 1. The Accuracy of Binding Free Energy Calculations Based on Molecular Dynamics Simulations. J. Chem. Inf. Model. 2010, 51, 69–82. [Google Scholar] [CrossRef]
- Liu, H.; Hou, T. CaFE: A tool for binding affinity prediction using end-point free energy methods. Bioinformatics 2016, 32, 2216–2218. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Liu, Y.; Wang, H.; Xiong, X.; Wei, P.; Li, F. Synthesis, Crystal Structure, Vibration Spectral, and DFT Studies of 4-Aminoantipyrine and Its Derivatives. Molecules 2013, 18, 877–893. [Google Scholar] [CrossRef]
- Ertl, P. Polar Surface Area; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2008. [Google Scholar]
- Blake, J.F. Chemoinformatics–predicting the physicochemical properties of ’drug-like’ molecules. Curr. Opin. Biotechnol. 2000, 11, 104–107. [Google Scholar] [CrossRef]
- Clark, D.E.; Pickett, S.D. Computational methods for the prediction of ‘drug-likeness’. Drug Discov. Today 2000, 5, 49–58. [Google Scholar] [CrossRef]
- Bickerton, G.R.; Paolini, G.V.; Besnard, J.; Muresan, S.; Hopkins, A.L. Quantifying the chemical beauty of drugs. Nat. Chem. 2012, 4, 90–98. [Google Scholar] [CrossRef] [Green Version]
- Thomas, G. Fundamentals of Medicinal Chemistry; John Wiley & Sons: Hoboken, NJ, USA, 2004; ISBN 0470871695. [Google Scholar]
- Sim, L.; Quezada-Calvillo, R.; Sterchi, E.E.; Nichols, B.L.; Rose, D.R. Human Intestinal Maltase–Glucoamylase: Crystal Structure of the N-Terminal Catalytic Subunit and Basis of Inhibition and Substrate Specificity. J. Mol. Biol. 2008, 375, 782–792. [Google Scholar] [CrossRef]
- Lipinski, C.A.; Lombardo, F.; Dominy, B.W.; Feeney, P.J. Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings. Adv. Drug Deliv. Rev. 1997, 23, 3–25. [Google Scholar] [CrossRef]
- Lipinski, C.A.; Lombardo, F.; Dominy, B.W.; Feeney, P.J. Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings. Adv. Drug Deliv. Rev. 2012, 64, 4–17. [Google Scholar] [CrossRef]
- Landeros-Martinez, L.-L.; Glossman-Mitnik, D.; Orrantia-Borunda, E.; Flores-Holguin, N. Molecular Docking; IntechOpen: London, UK, 2018. [Google Scholar]
- Snyder, P.W.; Mecinović, J.; Moustakas, D.T.; Thomas, S.W.; Harder, M.; Mack, E.T.; Lockett, M.R.; Héroux, A.; Sherman, W.; Whitesides, G.M. Mechanism of the hydrophobic effect in the biomolecular recognition of arylsulfonamides by carbonic anhydrase. Proc. Natl. Acad. Sci. USA 2011, 108, 17889–17894. [Google Scholar] [CrossRef] [Green Version]
- Hou, T.; Guo, S.; Xu, X. Predictions of Binding of a Diverse Set of Ligands to Gelatinase-A by a Combination of Molecular Dynamics and Continuum Solvent Models. J. Phys. Chem. B 2002, 106, 5527–5535. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Kollman, P.A. Computational study of protein specificity: The molecular basis of HIV-1 protease drug resistance. Proc. Natl. Acad. Sci. USA 2001, 98, 14937–14942. [Google Scholar] [CrossRef] [Green Version]
- Kuhn, B.; Kollman, P.A. Binding of a Diverse Set of Ligands to Avidin and Streptavidin: An Accurate Quantitative Prediction of Their Relative Affinities by a Combination of Molecular Mechanics and Continuum Solvent Models. J. Med. Chem. 2000, 43, 3786–3791. [Google Scholar] [CrossRef]
- Patra, N.; Ioannidis, E.I.; Kulik, H.J. Computational Investigation of the Interplay of Substrate Positioning and Reactivity in Catechol O-Methyltransferase. PLoS ONE 2016, 11, e0161868. [Google Scholar] [CrossRef]
- Reverri, E.J.; Randolph, J.M.; Kappagoda, C.T.; Park, E.; Edirisinghe, I.; Burton-Freeman, B.M. Assessing beans as a source of intrinsic fiber on satiety in men and women with metabolic syndrome. Appetite 2017, 118, 75–81. [Google Scholar] [CrossRef]
- Baig, I. Phytochemical Studies on Ferula Mongolica and Other Mongolian Medicinal Plants. Ph.D. Thesis, University of Karachi, Karachi, Pakistan, 2002. [Google Scholar]


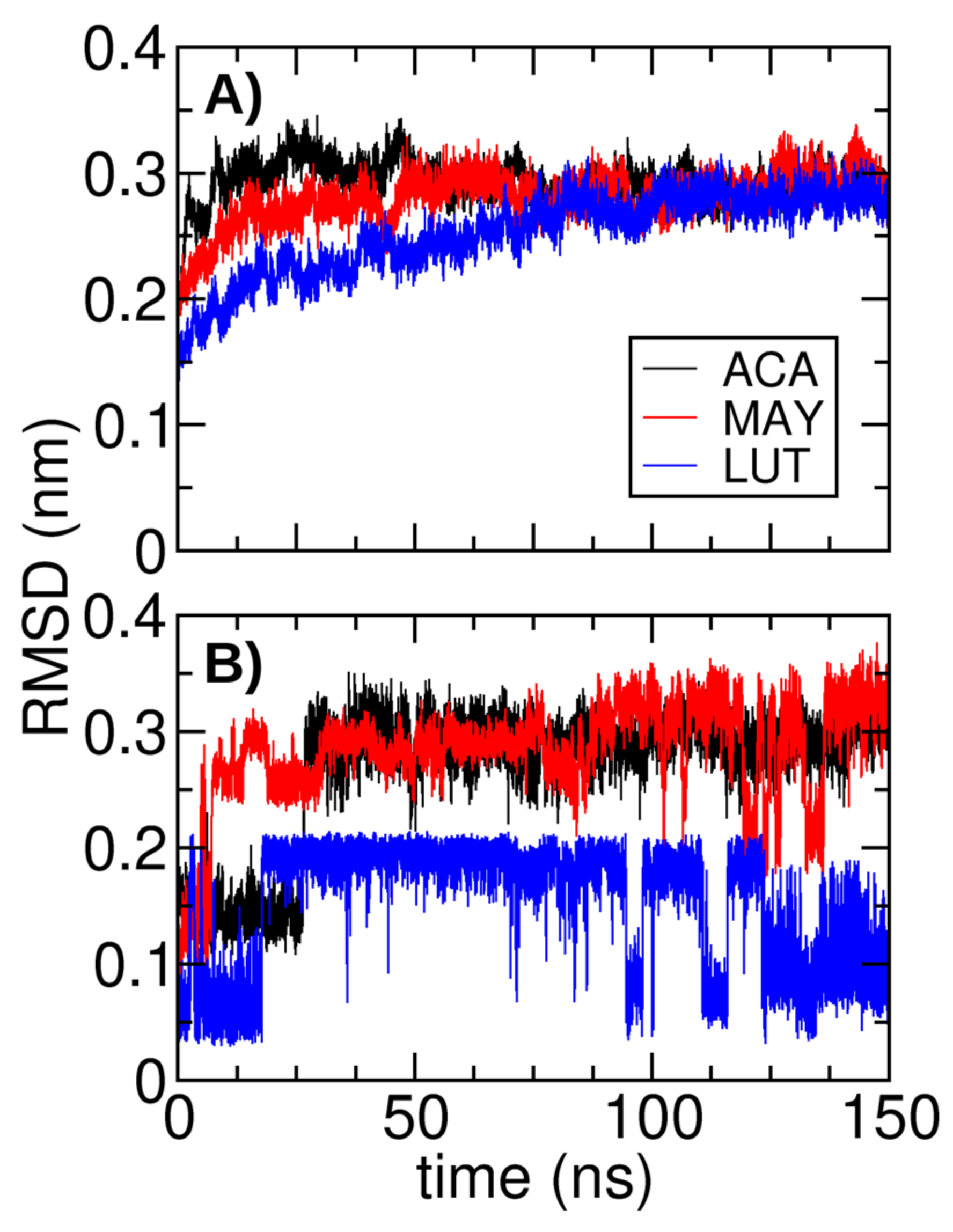
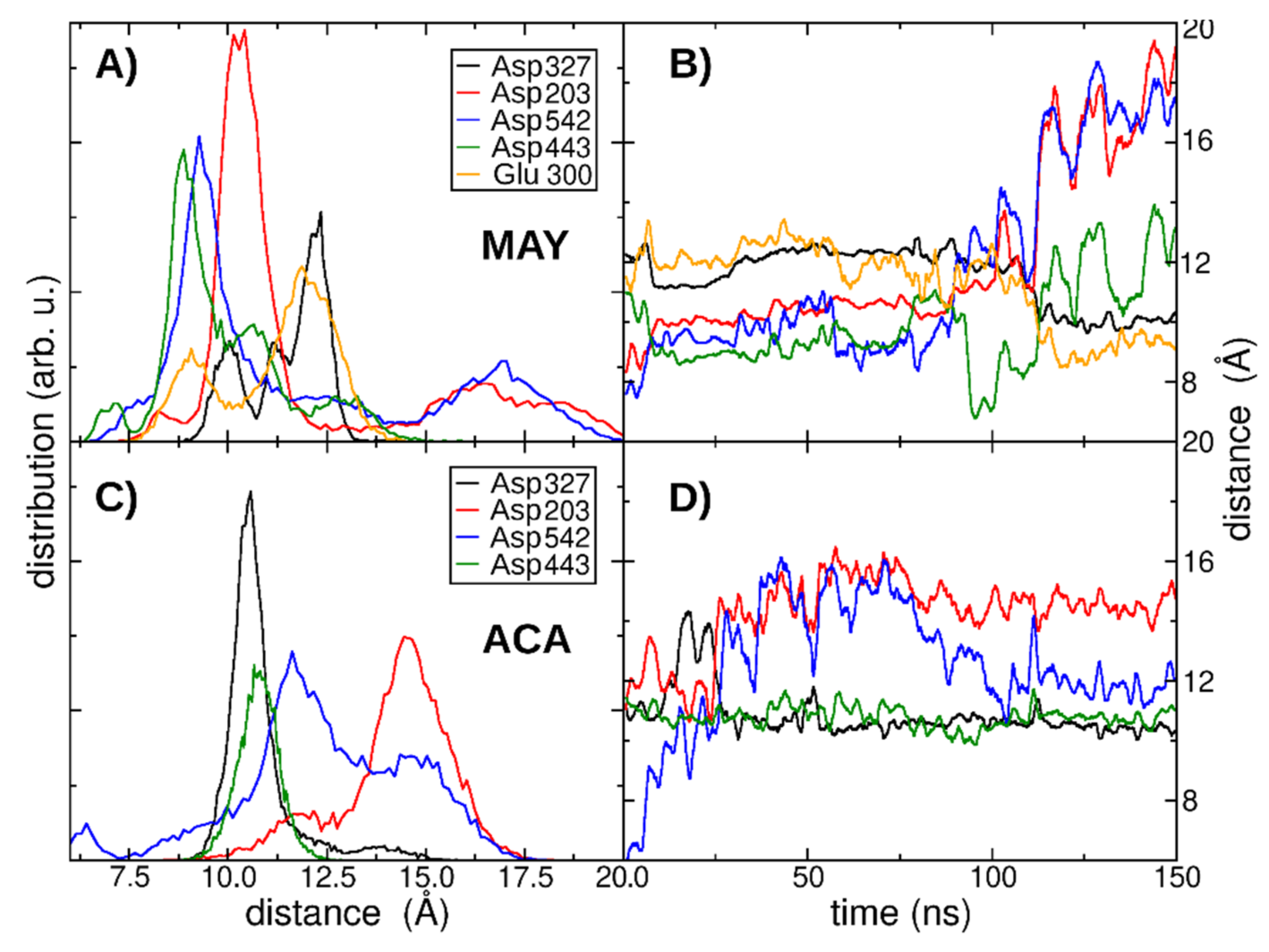
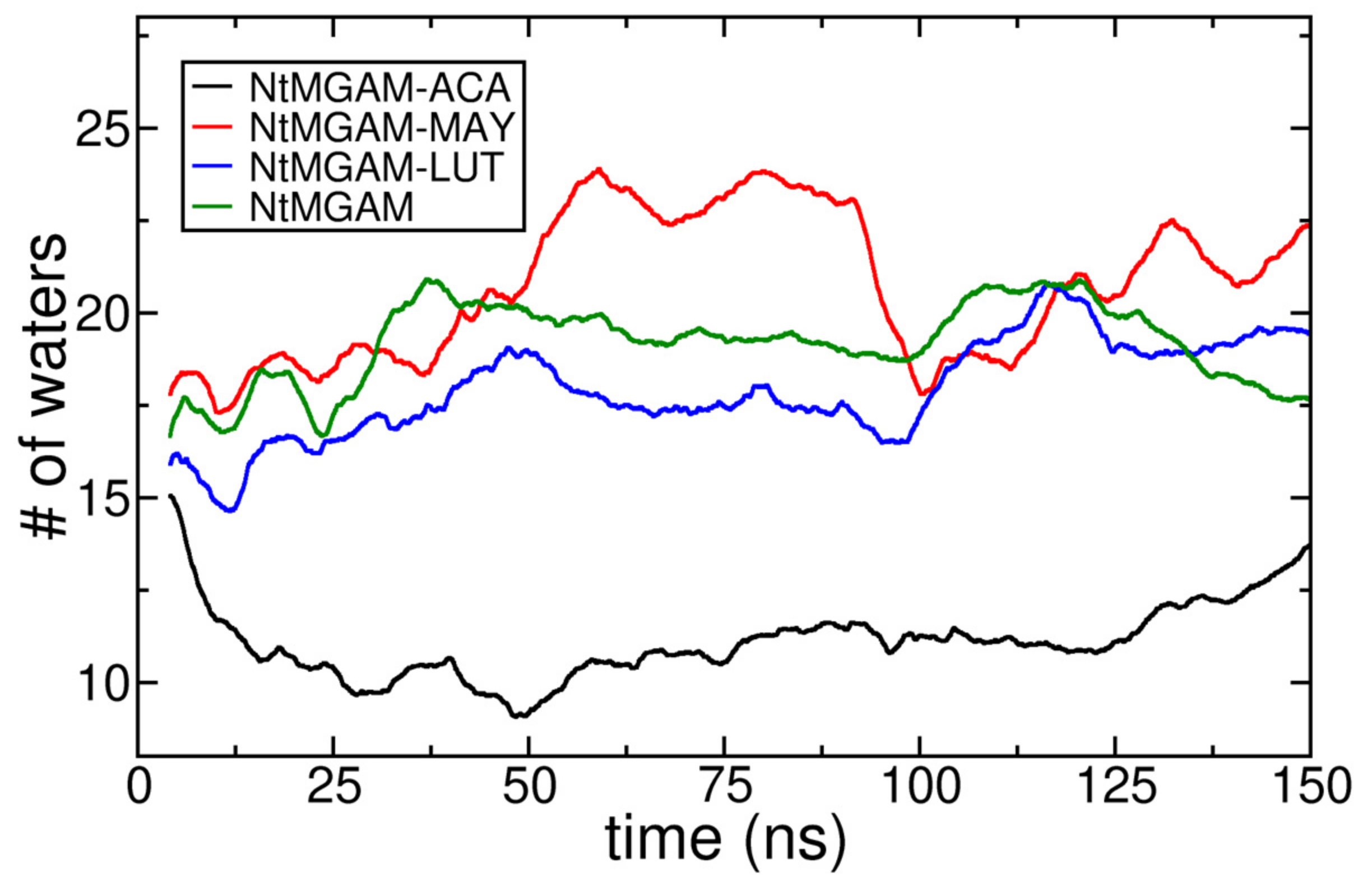
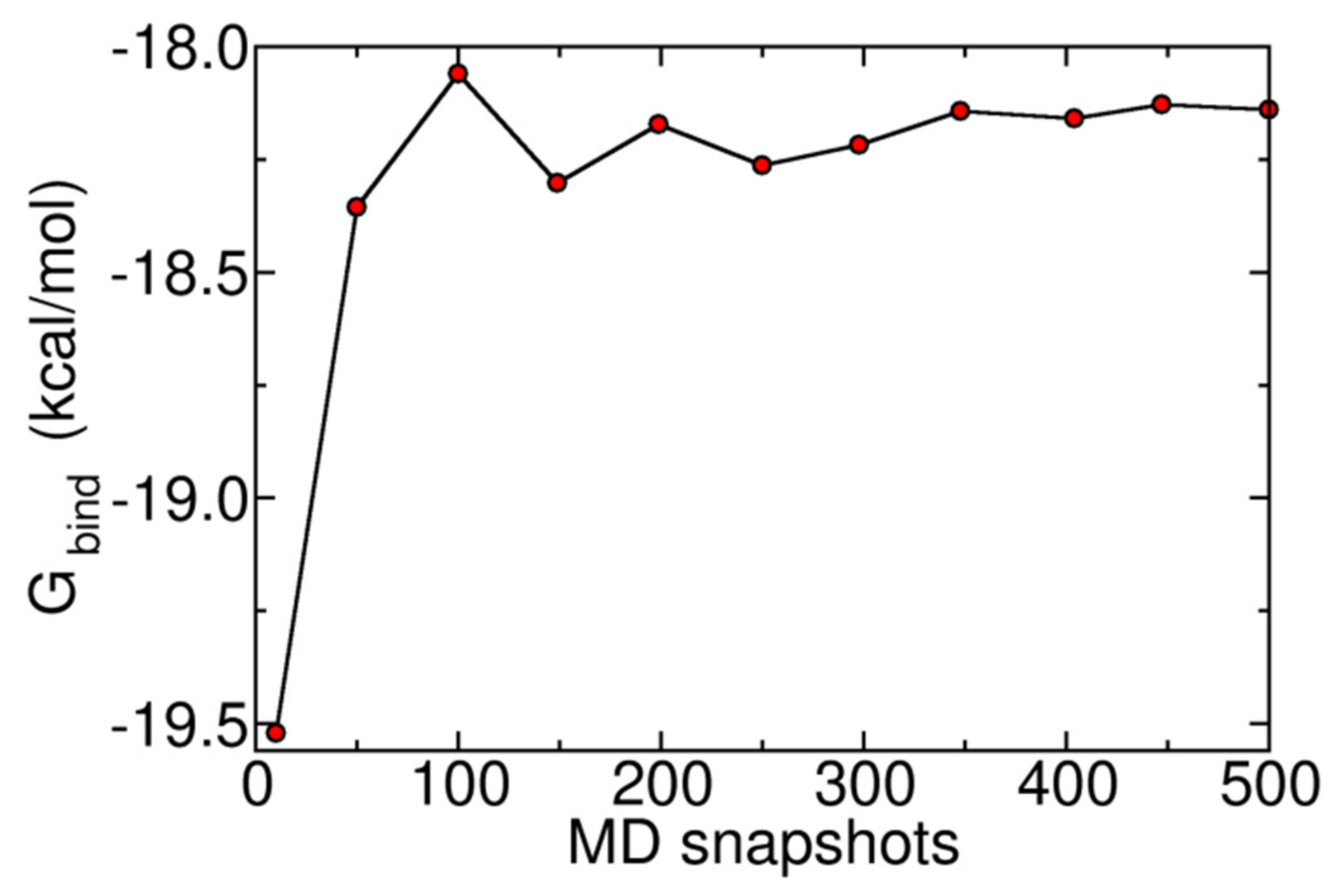
| Ligand | Binding Energy (kcal/mol) | Active Site | * Experimental |
|---|---|---|---|
| ACA | −7.8 | Asp203, Thr205, Tyr299, Asp327, Asp443, Met444, Arg526, Asp542, Trp539, Th544, Phe575, Ala576, His600 | Asp203, Tyr299, Asp327, Trp441, Asp443, Arg526, Asp542, Asp571, Phe575, His600, Tyr 605 |
| MAY | −9.1 | Arg202, Thr204, Thr205, Tyr299, Asp327, Trp406, Lys480, Asp542 | |
| LUT | −7.7 | Tyr299, Ile364, Trp406, Asp443, Arg526, Phe575, Gln603 |
| Ligand | EA | IP | η | χ | ω | μ |
|---|---|---|---|---|---|---|
| ACA | 0.21 | 6.14 | 2.97 | 3.17 | 1.70 | −3.17 |
| MAY | 1.80 | 6.34 | 2.27 | 4.07 | 3.65 | −4.04 |
| LUT | 1.70 | 6.35 | 2.32 | 4.03 | 3.49 | −4.03 |
| Ligand | Active Site | η | μ | ΔN |
|---|---|---|---|---|
| ACA | Asp203 | 2.90 | −2.78 | 0.033 |
| Thr205 | 2.36 | −3.11 | 0.006 | |
| Tyr299 | 2.67 | −3.61 | −0.039 | |
| Asp327 | 2.71 | −2.81 | 0.032 | |
| Asp443-Met444 | 2.85 | −2.85 | 0.027 | |
| Arg526 | 3.43 | −3.82 | −0.051 | |
| Trp539 | 2.58 | −3.19 | −0.002 | |
| Asp542 | 2.71 | −2.99 | 0.016 | |
| Thr544 | 3.27 | −3.81 | −0.051 | |
| Phe575-Ala576 | 2.89 | −3.50 | −0.028 | |
| His600 | 2.90 | −3.60 | −0.037 | |
| MAY -3.85 | Arg202-Asp203 | 2.51 | −3.43 | 0.067 |
| Thr204-Thr205 | 2.33 | −3.24 | 0.090 | |
| Tyr299 | 2.67 | −3.61 | 0.047 | |
| Asp327 | 2.71 | −2.81 | 0.127 | |
| Trp406 | 2.56 | −3.37 | 0.072 | |
| Asp443 | 2.84 | −2.84 | 0.123 | |
| Lys480 | 2.97 | −3.63 | 0.042 | |
| Asp542 | 2.71 | −2.94 | 0.113 | |
| LUT | Tyr299 | 2.67 | −3.61 | 0.047 |
| Ile364 | 3.33 | −3.62 | 0.036 | |
| Trp406 | 2.56 | −3.37 | 0.068 | |
| Asp443 | 2.77 | −2.74 | 0.127 | |
| Ser448 | 3.31 | −3.96 | 0.006 | |
| Arg526 | 3.43 | −3.82 | 0.018 | |
| Phe575 | 2.91 | −3.70 | 0.032 | |
| Gln603 | 3.20 | −3.95 | 0.007 |
| Occupancy (%) | |||
|---|---|---|---|
| Amino acids | ACA | LUT | MAY |
| Asp443 | 98.30 | 99.24 | 4.07 |
| Asp327 | 81.09 | 0.00 | 89.11 |
| Asp203 | 0.00 | 0.18 | 60.08 |
| Asp542 | 3.56 | 21.12 | 17.48 |
| Glu300 | 0.00 | 11.80 | 24.59 |
| His600 | 0.00 | 0.00 | 0.00 |
| Ligand | vdW | elec | PB | SA | Ggas | Gsolv | Gbind |
|---|---|---|---|---|---|---|---|
| ACA | −20.6092 | −106.5299 | 113.4123 | −5.1635 | −127.1391 | 108.2488 | −18.8903 |
| LUT | −1.6924 | −106.7976 | 93.7014 | −3.3515 | −108.4900 | 90.3499 | −18.1401 |
| MAY | −22.3635 | −51.0776 | 72.2392 | −4.2913 | −73.4411 | 67.9480 | −5.0346 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Landeros-Martínez, L.-L.; Gutiérrez-Méndez, N.; Palomares-Báez, J.P.; Sánchez-Bojorge, N.-A.; Flores-De los Ríos, J.P.; Piñón-Castillo, H.A.; Chávez-Rojo, M.A.; Rodríguez-Valdez, L.-M. The Oxidative Process of Acarbose, Maysin, and Luteolin with Maltase-Glucoamylase: Molecular Docking and Molecular Dynamics Study. Appl. Sci. 2021, 11, 4067. https://doi.org/10.3390/app11094067
Landeros-Martínez L-L, Gutiérrez-Méndez N, Palomares-Báez JP, Sánchez-Bojorge N-A, Flores-De los Ríos JP, Piñón-Castillo HA, Chávez-Rojo MA, Rodríguez-Valdez L-M. The Oxidative Process of Acarbose, Maysin, and Luteolin with Maltase-Glucoamylase: Molecular Docking and Molecular Dynamics Study. Applied Sciences. 2021; 11(9):4067. https://doi.org/10.3390/app11094067
Chicago/Turabian StyleLanderos-Martínez, Linda-Lucila, Néstor Gutiérrez-Méndez, Juan Pedro Palomares-Báez, Nora-Aydeé Sánchez-Bojorge, Juan Pablo Flores-De los Ríos, Hilda Amelia Piñón-Castillo, Marco Antonio Chávez-Rojo, and Luz-María Rodríguez-Valdez. 2021. "The Oxidative Process of Acarbose, Maysin, and Luteolin with Maltase-Glucoamylase: Molecular Docking and Molecular Dynamics Study" Applied Sciences 11, no. 9: 4067. https://doi.org/10.3390/app11094067
APA StyleLanderos-Martínez, L.-L., Gutiérrez-Méndez, N., Palomares-Báez, J. P., Sánchez-Bojorge, N.-A., Flores-De los Ríos, J. P., Piñón-Castillo, H. A., Chávez-Rojo, M. A., & Rodríguez-Valdez, L.-M. (2021). The Oxidative Process of Acarbose, Maysin, and Luteolin with Maltase-Glucoamylase: Molecular Docking and Molecular Dynamics Study. Applied Sciences, 11(9), 4067. https://doi.org/10.3390/app11094067








