Deformed Generalization of the Semiclassical Entropy

Abstract

We explicitly obtain here a novel expression for the semiclassical Wehrl’s entropy using deformed algebras built up with the q—coherent states (see Arik and Coon [J.Math.Phys. 17, 524 (1976) and Quesne [J. Phys. A 35, 9213 (2002)]). The generalization is investigated with emphasis on i) its behavior as a function of temperature and ii) the results obtained when the deformation-parameter tends to unity.

1. Introduction

The semiclassical approach has had a long and distinguished history and is a very important weapon in the physics’ armory. Indeed, semiclassical approximations to quantum mechanics remain an indispensable tool in many areas of physics and chemistry. Despite the extraordinary evolution of computer technology in the last years, exact numerical solution of the Schrödinger equation is still quite difficult for problems with more than a few degrees of freedom. Another great advantage of the semiclassical approximation lies in that it facilitates an intuitive understanding of the underlying physics, which is usually hidden in blind numerical solutions of the Schrödinger equation. Although semiclassical mechanics is as old as the quantum theory itself, the field is continuously evolving. There still exist many open problems in the mathematical aspects of the approximation as well as in the quest for new effective ways to apply the approximation to various physical systems (see, for instance, [1, 2] and references therein). In a different vein, applications of the so-called q-calculus to statistical mechanics have accrued increasing interest lately [3]. This q-calculus [4] has its origin in the q-deformed harmonic oscillator theory, which, in turn, is based on the construction of a SU q(2) algebra of q-deformed commutation or anti-commutation relations between creation and annihilation operators [5, 6, 7]. The above mentioned applications also employ “deformed information measures” (DIM) that have been applied to different scientific disciplines (see, for example, [3, 8, 9] and references therein). DIMs were introduced long ago in the cybernetic-information communities by Harvda-Charvat [10] and Vadja [11] in 1967-68, being rediscovered by Daroczy in 1970 [12] with several echoes mostly in the field of image processing. For a historic summary and the pertinent references see Ref. [13]. In astronomy, physics, economics, biology, etc., these deformed information measures are often called q-entropies since 1988 [9].

In this work we are concerned with semiclassical statistical physics’ problems and wish to add tools to the semiclassical armory by, in particular, investigating putative deformed extensions of two of its most important quantities, namely, Husimi distributions (HD) and Wehrl entropies (WE). We will work within the context of deformed algebras built up with the new family of q-deformed coherent states of Refs. [14], analyzing the main HD and WE properties. Our attention will be focused on the thermal description of the harmonic oscillator (HO) (together with its phase-space delocalization as temperature grows), in the understanding that the HO is, of course, much more than a mere example, since in addition to the extensively used Glauber states in molecular physics and chemistry [15, 16], nowadays the HO is of particular interest for the dynamics of bosonic or fermionic atoms contained in magnetic traps [17, 18], as well as for any system that exhibits an equidistant level spacing in the vicinity of the ground state, like nuclei or Luttinger liquids.

2. Semiclassical distribution in phase-space

Wehrl’s entropy W is a very useful measure of localization in phase-space [19]. It is built up using coherent states [19, 20, 21] and constitutes a powerful tool in statistical physics. The pertinent definition reads

(1)

where µ(x, p) = 〈z|ρ|z〉 is a “semi-classical” phase-space distribution function associated to the density matrix ρ of the system [15, 20]. Coherent states are eigenstates of the annihilation operator a, i.e., satisfies a|z〉 = z|z〉.

The distribution µ(x, p) is normalized in the fashion

(2)

and it is often referred to as the Husimi distribution [22]. The last two equations clearly indicate that the Wehrl entropy is simply the “classical entropy” (1) of a Wigner-distribution. Indeed, µ(x, p) is a Wigner-distribution D_W smeared over an ℏ sized region of phase space [21]. The smearing renders µ(x, p) a positive function, even if D_W does not have such a character. The semi-classical Husimi probability distribution refers to a special type of probability: that for simultaneous but approximate location of position and momentum in phase space [21]. The uncertainty principle manifests itself through the inequality 1 ≤ W , which was first conjectured by Wehrl [19] and later proved by Lieb [23].

The usual treatment of equilibrium in statistical mechanics makes use of the Gibbs’s canonical distribution, whose associated, “thermal” density matrix is given by

ρ = Z⁻¹e^−βH ,

(3)

with Z = Tr(e^−βH) the partition function, β = 1/k_BT the inverse temperature T, and k_B the Boltzmann constant. In order to conveniently write down an expression for W consider an arbitrary Hamiltonian H of eigen-energies E_n and eigenstates |n〉 (n stands for a collection of all the pertinent quantum numbers required to label the states). One can always write [21]

(4)

A useful route to W starts then with Eq. (4) and continues with Eq. (1). In the special case of the harmonic oscillator the coherent states are of the form [20]

(5)

where |n〉 are a complete orthonormal set of eigenstates and whose spectrum of energy is E_n = (n + 1/2)ℏω, n = 0, 1,… In this situation the analytic expression for the HD and the WE were obtained in Ref. [21]

(6)

W = 1 − ln(1 − e^−βℏω).

(7)

When T → 0, the entropy takes its minimum value W = 1, expressing purely quantum fluctuations. On the other hand when T → ∞, the entropy tends to the value − ln(βℏω) which expresses purely thermal fluctuations.

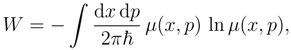
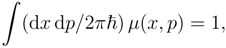
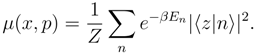
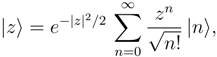
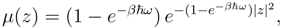
3. q-deformed coherent states

In Refs. [14] one encounters a new family of harmonic oscillator physical states, labelled by 0 < q < 1 and z ∈ ℂ,

(8)

where |n〉 = (n!)^−1/2(a^†)ⁿ|0〉 is the n-boson state and one introduces quasi-factorials [14]

with

(9)

{n}_q is called the “q-basic number” and generates its own factorial (the q-factorial) {n}_q! [14]. The q-factorial can also be written in terms of the q-gamma function Γq(x) [14]

(10)

that, in the limit q → 1, yields [n]_q, [n]_q!, and Γq(n) tending to n, n!, and Γ(n), respectively. The states |z〉_q allow one to build up q-deformed coherent states. They will be acceptable generalized coherent states if three basic mathematical properties are verified [15]. The states |z〉_q should be: i) normalizable, ii) continuous in the z-label. Additionally, iii) one must ascertain the existence of a resolution of unity with a positive weight function. The normalization condition, _q〈z|z〉_q = 1 leads to

(11)

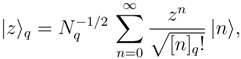
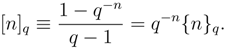
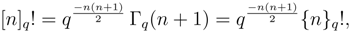
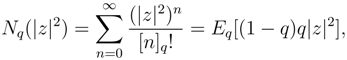
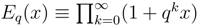where is one of the so-called Jackson’s q-exponentials introduced in 1909 [24] such that lim_q→1 E_q[(1 − q)x] = e^x. Since N_q(|z|²) is equal to E_q[(1 − q)q|z|²] (a well defined function in 0 < q < 1), the new states are normalizable on the whole complex plane. On the other hand, the states |z〉_q are always continuous in z. Finally, for the resolution of unity one needs

(12)

with a weight function K_q(|z|²) that can be obtained using the expressions for |z〉_q and its conjugate and then performing the integral by recourse to the q-analogue of the Euler gamma integral [14]. One finds

(13)

It is seen that, in the limit q → 1⁻, we have K_q(|z|²) → K(|z|²) = 1/π, corresponding to the weights for the conventional coherent states of the harmonic oscillator. This entails that we indeed have at hand new q-deformed coherent states that fulfill the standard properties. In the next section we start presenting the results of this communication, using these deformed coherent states to generalize our q-Husimi distribution.

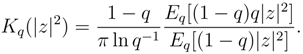
4. The q-Husimi distribution for 0 < q < 1

We start in this Section to present our new contributions by introducing the deformed q-Husimi distribution (q-HD) in the rather “natural” fashion

µ_q(z) ≡ _q〈z|ρ|z〉_q,

(14)

using deformed HO-q-coherent states (5). From these it is easy to find an analytic expression for our new q-Husimi distributions

(15)

It is important to remark that

(16)

where µ(z) is given by (6). We have numerically ascertained that our q-Husimi distribution is normalized using the same weight function K_q(|z|²) that, for instance Quesne, employed for the resolution of unity of the q-coherent states.

(17)

One can ascertain numerically that a q-HD’s height depends only upon the temperature (not on q!). q-Deformation affects only shapes. Thus,

0 < µ_q(z) ≤ 1,

(18)

and µ_q(z) remains a legitimate semi-classical probability distribution (unlike Wigner’s one).

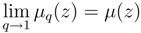
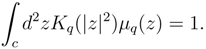
5. Deformed Wehrl entropies

The natural definition of a deformed Wehrl entropy reads as follows

(19)

and, inserting the explicit HO-form (15) into the above expression, we find

W_q = f(q) − ln(1 − e^−βℏω) ≡ f(q) − 1 + W,

(20)

where

(21)

It easy to check that in the limit q → 1 one has f(q) → 1 and Eq. (20) leads to the usual Wehrl entropy. The f(q) can not be obtained in analytic fashion and needs numerical evaluation. Fig. 1 depicts f(q) vs. q for different values of t = T/(ℏω).

We see from (21) and comparison with the conventional HO-Wehrl entropy W = 1 − ln(1 − e^−βℏω) that deformation merely entails a constant-in-z additive function f(q), depending solely on q, so that W_q behaves, as a function of deformation, exactly like the q-distributions of the previous Sections. At low enough temperatures our q-coherent states minimize the q-entropy, i.e., W_q ∼ 1, yielding maximal localization. Delocalization grows with T, of course.

At this stage we are in a position to draw an important consequence. In general, deformed (or Tsallis’) entropies are quite different objects as compared with Shannon’s one, save for q close to unity. This is not the case for q-Wehrl entropies! q-deformation becomes in this case a smooth shape-deformation. At the semiclassical level the difference between Tsallis and Shannon entropies becomes weaker than either at the quantal or the classical levels.

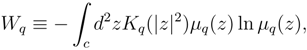
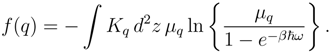
6. q-Wehrl entropy bounds

Using our definition of q-WE given by Eq. (20) we can easily investigate possible bounds for the Wehrl entropy, i.e., for our localization power. We see that, when T → 0, one has

(22)

where

(23)

while, for T → ∞,

W_q → − ln(βℏω) = ∞,

(24)

having a lower bound only. Since, obviously, W_q is a monotonically growing function of T we can state that

(25)

which constitutes the new deformed Lieb-relation. It is easy to check the limit q → 1:

(26)

and we reobtain the known Lieb bound of the standard Wehrl entropy 1 ≤ W.

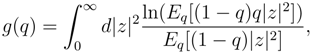
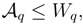
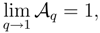
7. Conclusions

Semiclassical Husimi distributions and their associated Wehrl entropies have been here investigated within the frame of deformed algebras. As a summary of our results we can state that:

• we have advanced a q-generalization of the Husimi distribution µ_q(z), which arises from the family of q-coherent states and found that the q-deformation does not change the HD’s property of being legitimate probability distributions.
• the above leads to a concomitant generalization, that we call the q-Wehrl one, W_q(µ_q), whose lower bound coincides with the well-known Lieb one. These semiclassical q-entropy approach the standard one when q tends to unity.
• Although in general deformed (or Tsallis’) entropies are quite different objects as compared with Shannon’s one, save for q close to unity, such is not the case for q-Wehrl entropies, which differ from the orthodox ones in just an additive quantity.