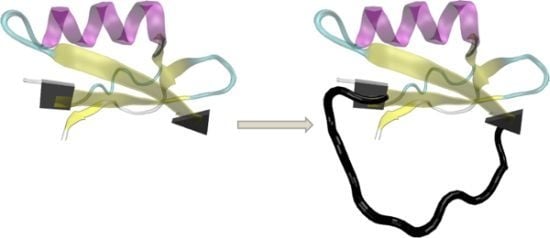
Modeling Structures and Motions of Loops in Protein Molecules

Abstract: Unlike the secondary structure elements that connect in protein structures, loop fragments in protein chains are often highly mobile even in generally stable proteins. The structural variability of loops is often at the center of a protein’s stability, folding, and even biological function. Loops are found to mediate important biological processes, such as signaling, protein-ligand binding, and protein-protein interactions. Modeling conformations of a loop under physiological conditions remains an open problem in computational biology. This article reviews computational research in loop modeling, highlighting progress and challenges. Important insight is obtained on potential directions for future research.