Combined Effect of Buoyancy Force and Navier Slip on Entropy Generation in a Vertical Porous Channel
Abstract
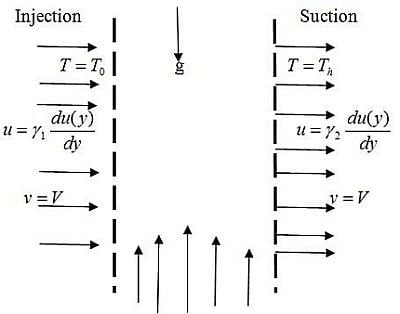
:1. Introduction
2. Mathematical Analysis

- (Reynolds number),
- (Peclet number),
- (Pressure gradient parameter),
- (Brinkman number),
- (Grashof number),
- (Slip parameter),
- (Slip parameter).
3. Entropy Generation
4. Results and Discussion



















5. Conclusions
Nomenclature
| dimensional velocity, [ms−1] | u | fluid velocity, [ms−1] | |
| P | fluid pressure, [Nm−2] | x,y | cartesian coordinates, [m] |
| T | fluid temperature, [K] | g | acceleration due to gravity, [ms−2] |
| EG | volumetric rate of entropy production, [W/m3 K] | w | dimensionless velocity |
| T0 | temperature at y = 0, [K] | Th | temperature at y = h, [K] |
| specific heat at constant pressure, [J/kgK] | Re | Reynolds number, [-] | |
| Pe | Peclet number, [-] | Br | Brinkman number |
| skin friction, [-] | Nu | Nusselt number, [-] | |
| N1 | entropy generation due to heat transfer | N1 | entropy generation due to viscous dissipation |
| Be | Bejan number, [-] | K | pressure gradient |
| Greek Letters | |||
| fluid viscosity, [Nsm−2] | thermal diffusivity, [m2s−1] | ||
| slip coefficients, [m] | volumetric expansion coefficient, [K−1] | ||
| fluid density, [kgm−3] | dimensionless temperature, [-] | ||
| dimensionless slip coefficients, [-] | dimensionless temperature difference, [-] | ||
| irreversibility ratio, [-] | |||
References
- White, F.S. Viscous Fluid Flow; McGraw-Hill: New York, NY, USA, 1974. [Google Scholar]
- Ingham, D.B.; Pop, I. Transport Phenomena in Porous Media; Pergamon: Oxford, UK, 2002. [Google Scholar]
- Nield, D.A.; Bejan, A. Convection in Porous Media, 3rd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Makinde, O.D.; Osalusi, E. MHD steady flow in a channel with slip at the permeable boundaries. Rom. J. Phys. 2006, 51, 319–328. [Google Scholar]
- Khaled, A.R.A.; Vafai, K. The effect of the slip condition on stokes and couette flows due to an oscillatory wall: Exact solutions. Int. J. Non. Lin. Mech. 2004, 39, 795–809. [Google Scholar] [CrossRef]
- Watanebe, K.; Yanuar, M.H. Slip of Newtonian fluids at solid boundary. J. Jpn. Soc. Mech. Eng. 1998, B41, 525. [Google Scholar] [CrossRef]
- Chen, S; Tian, Z. Entropy generation analysis of thermal micro-Couette flows in slip regime. Int. J. Therm. Sci. 2010, 49, 2211–2221. [Google Scholar] [CrossRef]
- Chauhan, D.S.; Kumar, V. Effects of slip conditions on forced convection and entropy generation in a circular channel occupied by a highly porous medium: Darcy extended Brinkman-Forchheimer model. Turk. J. Eng. Environ. Sci. 2009, 33, 91–104. [Google Scholar]
- Mahmud, S.; Fraser, R.A. Flow, thermal and entropy generation characteristic inside a porous channel with viscous dissipation. Int. J. Therm. Sci. 2005, 44, 21–32. [Google Scholar] [CrossRef]
- Chauhan, D.S.; Olkha, A. Entropy generation and heat transfer effects on non-Newtonian fluid flow in annular pipe with natural permeable boundaries. Int. J. Energ. Tech. 2011, 3, 1–19. [Google Scholar]
- Chauhan, D.S.; Kumar, V. Heat transfer and entropy generation during compressible fluid flow in a channel partially filled with porous medium. Int. J. Energ. Tech. 2011, 3, 1–10. [Google Scholar]
- Chauhan, D.S.; Rastogi, P. Heat transfer and entropy generation in MHD flow through a porous medium past a stretching sheet. Int. J. Energ. Tech. 2011, 3, 1–13. [Google Scholar]
- Hooman, K. Entropy-energy analysis of forced convection in a porous-saturated circular tube considering temperature-dependent viscosity effects. Int. J. Exergy 2006, 3, 436–451. [Google Scholar] [CrossRef]
- Hooman, K.; Gurgenci, H.; Merrikh, A.A. Heat transfer and entropy generation optimization of forced convection in a porous-saturated duct of rectangular cross-section. Int. J. Heat Mass Tran. 2007, 50, 2051–2059. [Google Scholar] [CrossRef] [Green Version]
- Tasnim, S.H.; Mahmud, S.; Mamun, M.A.H. Entropy generation in a porous channel with hydromagnetic effects. Exergy 2002, 2, 300–308. [Google Scholar] [CrossRef]
- Ozkol, I.; Komurgoz, G.; Arikoglu, A. Entropy generation in the laminar natural convection from a constant temperature vertical plate in an infinite fluid. Proc. IME J. Power. Energ. 2007, 221, 609–616. [Google Scholar] [CrossRef]
- Bejan, A. Convection Heat Transfer; John Wiley and Sons: New York, NY, USA, 1984. [Google Scholar]
- Bejan, A. Entropy generation minimization; CRC Press: New York, NY, USA, 1996. [Google Scholar]
- Makinde, O.D.; Osalusi, E. Second law analysis of laminar flow in a channel filled with saturated porous media. Entropy 2005, 7, 148–160. [Google Scholar] [CrossRef]
- Makinde, O.D. Second law analysis for variable viscosity hydromagnetic boundary layer flow with thermal radiation and Newtonian heating. Entropy 2011, 13, 1446–1464. [Google Scholar] [CrossRef]
- Mahmud, S.; Tasnim, S.H.; Mamun, H.A.A. Thermodynamics analysis of mixed convection in a channel with transverse hydromagnetic effect. Int. J Therm. Sci. 2003, 42, 731–740. [Google Scholar] [CrossRef]
- Chen, S.; Tolke, J.; Krafczyk, M. Numerical investigation of double-diffusive (natural) convection in vertical annuluses with opposing temperature and concentration gradients. Int. J. Heat Fluid Flow 2010, 31, 217–226. [Google Scholar] [CrossRef]
- Chen, S.; Du, R. Entropy generation of turbulent double-diffusive natural convection in a rectangle cavity. Energy 2011, 36, 1721–1734. [Google Scholar] [CrossRef]
- Chen, S. Entropy generation of double-diffusive convection in the presence of rotation. Appl. Math. Comput. 2011, 217, 8575–8597. [Google Scholar] [CrossRef]
- Chen, S.; Li, J.; Han, H.; Liu, Z.; Zheng, Z. Effects of hydrogen addition on entropy generation in ultra-lean counter-flow methane-air premixed combustion. Int. J. Hydrogen Energ. 2010, 35, 3891–3902. [Google Scholar] [CrossRef]
- Chen, S.; Mi, J.; Liu, H.; Zheng, C. First and second thermodynamic-law analyses of hydrogen-air counter-flow diffusion combustion in various combustion modes. Int. J. Hydrogen Energ. 2012, 37, 5234–5245. [Google Scholar] [CrossRef]
- Chen, S.; Zheng, C. Entropy generation in impinging flow confined by planar opposing jets. Int. J. Therm. Sci. 2010, 49, 2067–2075. [Google Scholar] [CrossRef]
- Chen, S.; Liu, Z.; Liu, J.; Li, J.; Wang, L.; Zhen, C. Analysis of entropy generation in hydrogen-enriched ultra-lean counter-flow methane-air non-premixed combustion. Int. J. Hydrogen Energ. 2010, 35, 12491–12501. [Google Scholar] [CrossRef]
- Chen, S.; Han, H.; Liu, Z.; Li, J.; Zheng, C. Analysis of entropy generation in non-premixed hydrogen versus heated air counter-flow combustion. Int. J. Hydrogen Energ. 2010, 35, 4736–4746. [Google Scholar] [CrossRef]
- Chen, S. Analysis of entropy generation in counter-flow premixed hydrogen-air combustion. Int. J. Hydrogen Energ. 2010, 35, 1401–1411. [Google Scholar] [CrossRef]
- Chen, S. Entropy generation inside disk driven rotating convectional flow. Int. J. Therm. Sci. 2011, 50, 626–638. [Google Scholar] [CrossRef]
- Chen, S.; Liu, Z.; Bao, S.; Zheng, C. Natural convection and entropy generation in a vertically concentric. Int. J. Therm. Sci. 2010, 49, 2439–2452. [Google Scholar] [CrossRef]
- Nachtsheim, P.R.; Swigert, P. Satisfaction of the Asymptotic Boundary Conditions in Numerical Solution of the System of Nonlinear Equations of Boundary Layer Type, NASA TND-3004. 1965.
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Eegunjobi, A.S.; Makinde, O.D. Combined Effect of Buoyancy Force and Navier Slip on Entropy Generation in a Vertical Porous Channel. Entropy 2012, 14, 1028-1044. https://doi.org/10.3390/e14061028
Eegunjobi AS, Makinde OD. Combined Effect of Buoyancy Force and Navier Slip on Entropy Generation in a Vertical Porous Channel. Entropy. 2012; 14(6):1028-1044. https://doi.org/10.3390/e14061028
Chicago/Turabian StyleEegunjobi, Adetayo Samuel, and Oluwole Daniel Makinde. 2012. "Combined Effect of Buoyancy Force and Navier Slip on Entropy Generation in a Vertical Porous Channel" Entropy 14, no. 6: 1028-1044. https://doi.org/10.3390/e14061028
APA StyleEegunjobi, A. S., & Makinde, O. D. (2012). Combined Effect of Buoyancy Force and Navier Slip on Entropy Generation in a Vertical Porous Channel. Entropy, 14(6), 1028-1044. https://doi.org/10.3390/e14061028