Stability of Accelerating Cosmology in Two Scalar-Tensor Theory: Little Rip versus de Sitter
Abstract
:1. Introduction
- Type I (“Big Rip”) : For , , and . This also includes the case of , being finite at .
- Type III : For , , and .
- Type IV : For , , , and higher derivatives of H diverge. This also includes the case in which () or both of and tend to some finite values, whereas higher derivatives of H diverge.
2. Reconstruction of Scalar Model and (in)stability
2.1. One Scalar Model
2.2. Two Scalar Model
3. Reconstruction of Little Rip Cosmology
3.1. A Model of Little Rip Cosmology
3.2. Asymptotically de Sitter Phantom Model
3.3. Asymptotically de Sitter Quintessence Dark Energy
3.4. A Realistic Model Unifying Inflation with Little Rip Dark Energy Era
| Models | Stability of the reconstructed solution | Existence of de Sitter solution | Stability of de Sitter solution |
|---|---|---|---|
| Equation (35) | stable | no | − |
| Equation (51) | stable if | yes if | unstable |
| Equation (59) | stable if and | yes if | unstable |
| Equation (68) | stable if | no | − |
4. Reconstruction in Terms of E-Foldings and Solution Flow
4.1. Reconstruction of Two Scalar Model and (in)stability
4.2. Fixed Points and Flow of General Solutions
- Point A
- Here the solution is given by Equation (80).
- Point B
- Besides Point A , there could be another solution for Equations (82–85). In order to show the existence of another solution, we now define byHere and are dimensionless constants. We now assume that the following equation could be satisfied,Then if there exist and which satisfy Equation (89), we find Equations (82–85) is satisfied by the following solution:Especially when , this point describes de Sitter space-time.
4.2.1. Model with Exponential Growth

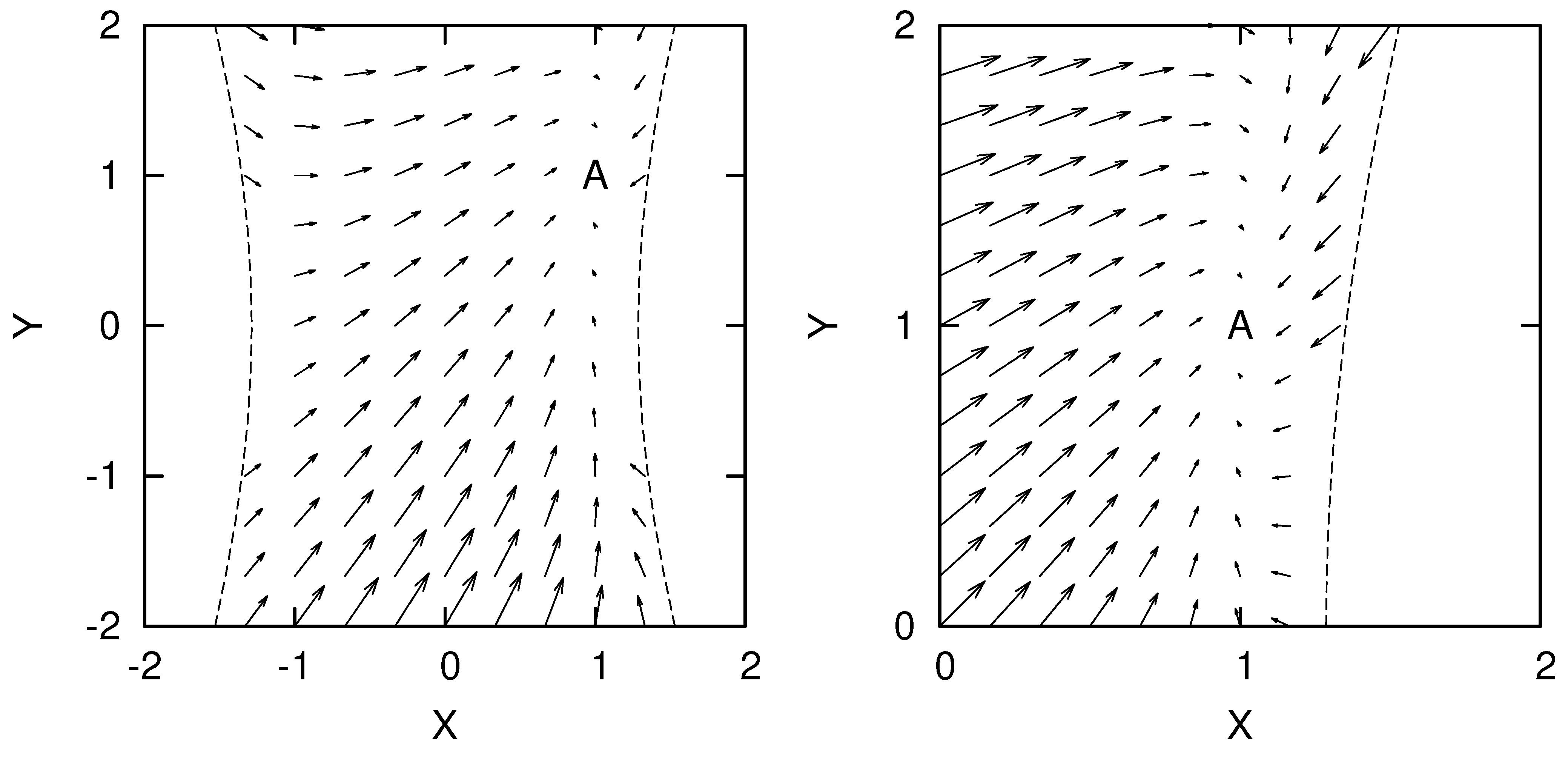
4.2.2. Little Rip Model

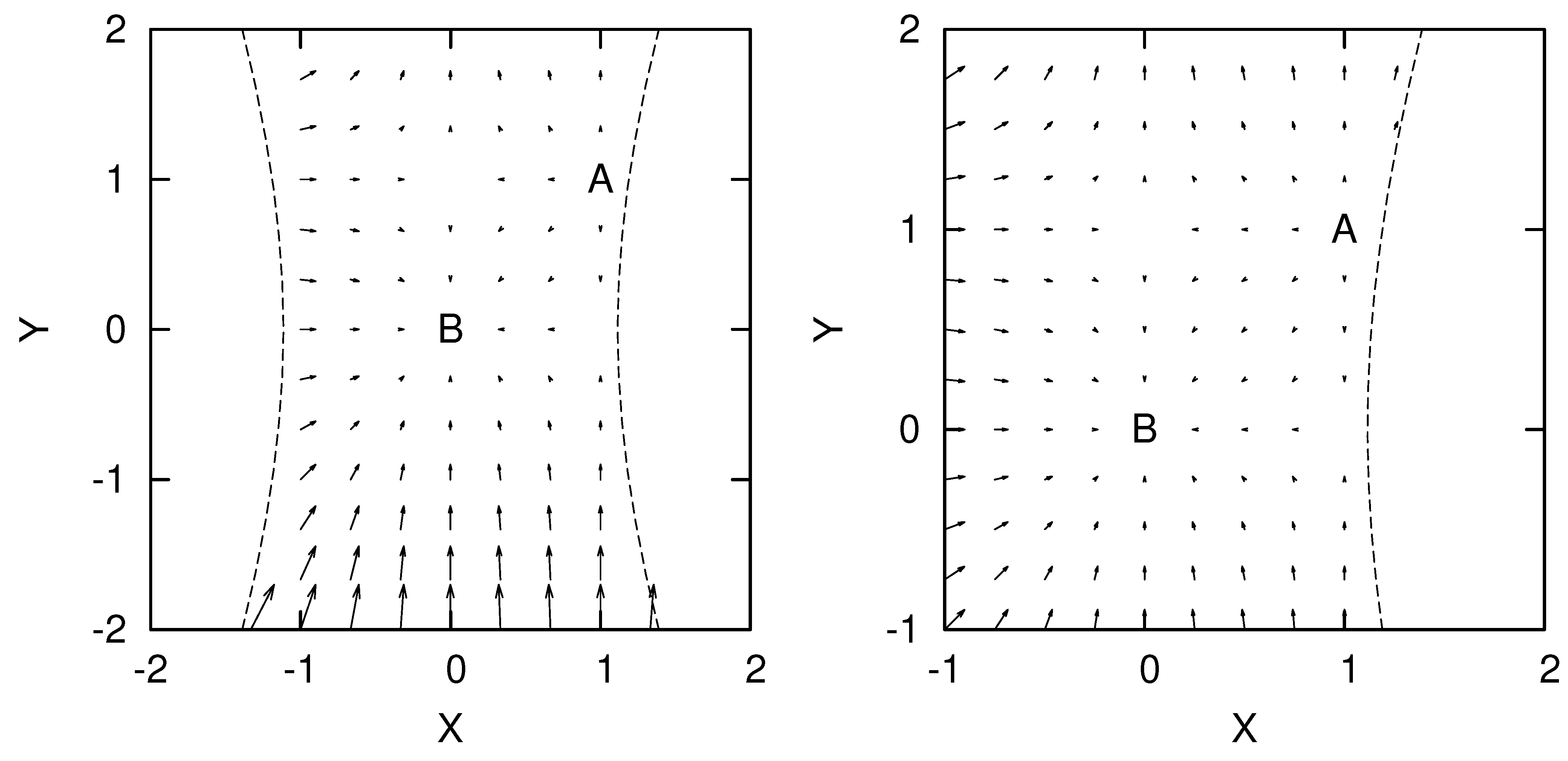


4.3. The Potential and the (in)stability
5. Discussion
- (1)
- The potential does not have maximum and it goes to infinity.
- (2)
- There is a path in the potential that the potential becomes infinite but the kinetic energy of the canonical scalar field is vanishing.
Acknowledgments
References
- De Bernardis, P.; Ade, P.A.R.; Bock, J.J.; Bond, J.R.; Borrill, J.; Boscaleri, A.; Coble, K.; Crill, B.P.; de Gasperis, G.; Farese, P.C.; et al. A flat universe from high resolution maps of the cosmic microwave background radiation. Nature 2000, 404, 955–959. [Google Scholar] [CrossRef] [PubMed]
- Hanany, S.; Ade, P.; Balbi, A.; Bock, J.; Borrill, J.; Boscaleri, A.; de Bernardis, P.; Ferreira, P.G.; Hristov, V.V.; Jaffe, A.H.; et al. MAXIMA-1: A measurement of the cosmic microwave background anisotropy on angular scales of 10 arcminutes to 5 degrees. Astrophys. J. 2000, 545. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of omega and lambda from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Della Valle, M.; Deustua, S.; Ellis, R.S.; Fabbro, S.; Fruchter, A.; Goldhaber, G.; Goobar, A.; Groom, D.E.; et al. Discovery of a supernova explosion at half the age of the Universe and its cosmological implications. Nature 1998, 391, 51–54. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiattia, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Silvestri, A.; Trodden, M. Approaches to understanding cosmic acceleration. Rep. Prog. Phys. 2009, 72. [Google Scholar] [CrossRef]
- Li, M.; Li, X.-D.; Wang, S.; Wang, Y. Dark energy. Commun. Theor. Phys. 2011, 56, 525–604. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Kamionkowski, M. The physics of cosmic acceleration. Ann. Rev. Nucl. Part. Sci. 2009, 59, 397–429. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. 2006, D15, 1753–1936. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified gravity and cosmology. Phys. Rep. 2012, 513, 1–189. [Google Scholar] [CrossRef]
- Conley, A.; Guy, J.; Sullivan, M.; Regnault, N.; Astier, P.; Balland, C.; Basa, S.; Carlberg, R.G.; Fouchez, D.; Hardin, D.; et al. Supernova constraints and systematic uncertainties from the first 3 years of the supernova legacy survey. Astrophys. J. Suppl. 2011, 192, 1–29. [Google Scholar] [CrossRef]
- Sullivan, M.; Guy, J.; Conley, A.; Regnault, N.; Astier, P.; Balland, C.; Basa, S.; Carlberg, R.G.; Fouchez, D.; Hardin, D.; et al. SNLS3: Constraints on dark energy combining the supernova legacy survey three year data with other probes. Astrophys. J. 2011, 737. [Google Scholar] [CrossRef]
- Komatsu, E.; Smith, K.M.; Dunkley, J.; Bennett, C.L.; Gold, B.; Hinshaw, G.; Jarosik, N.; Larson, D.; Nolta, M.R.; Page, L.; et al. Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Cosmological interpretation. Astrophys. J. Suppl. 2011, 192. [Google Scholar] [CrossRef]
- Dunkley, J.; Hlozek, R.; Sievers, J.; Acquaviva, V.; Ade, P.A.R.; Aguirre, P.; Amiri, M.; Appel, J.W.; et al. The atacama cosmology telescope: Cosmological parameters from the 2008 power spectra. Astrophys. J. 2011, 739. [Google Scholar] [CrossRef]
- Reid, B.A.; Percival, W.J.; Eisenstein, D.J.; Verde, L.; Spergel, D.N.; Skibba, R.A.; Bahcall, N.A.; Budavari, T.; et al. Cosmological constraints from the clustering of the sloan digital sky survey DR7 luminous red galaxies. Mon. Not. R. Astron. Soc. 2010, 404, 60–85. [Google Scholar] [CrossRef] [Green Version]
- Giannantonio, T.; Scranton, R.; Crittenden, R.G.; Nichol, R.C.; Boughn, S.P.; Myers, A.D.; Richards, G.T. Combined analysis of the integrated Sachs-Wolfe effect and cosmological implications. Phys. Rev. 2008, D77. [Google Scholar] [CrossRef]
- Ho, S.; Hirata, C.; Padmanabhan, N.; Seljak, U.; Bahcall, N. Correlation of CMB with large-scale structure: I. ISW tomography and cosmological implications. Phys. Rev. 2008, D78. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Kamionkowski, M.; Weinberg, N.N. Phantom energy and cosmic doomsday. Phys. Rev. Lett. 2003, 91. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Tsujikawa, S. Properties of singularities in (phantom) dark energy universe. Phys. Rev. 2005, D71. [Google Scholar] [CrossRef]
- Barrow, J.D. Sudden future singularities. Class. Quantum Grav. 2004, 21, L79–L82. [Google Scholar] [CrossRef]
- Barrow, J.D. More general sudden singularities. Class. Quantum Grav. 2004, 21, 5619–5622. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Frampton, P.H.; Ludwick, K.J.; Scherrer, R.J. The little rip. Phys. Rev. 2011, D84, 063003. [Google Scholar] [CrossRef]
- Frampton, P.H.; Ludwick, K.J.; Nojiri, S.; Odintsov, S.D.; Scherrer, R.J. Models for little rip dark energy. Phys. Lett. 2012, B708, 204–211. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Saez-Gomez, D. Cyclic, ekpyrotic and little rip universe in modified gravity. AIP Conf. Proc. 2011, 1458, 207–221. [Google Scholar]
- Brevik, I.; Elizalde, E.; Nojiri, S.; Odintsov, S.D. Viscous little rip cosmology. Phys. Rev. 2011, D84, 103508:1–103508:6. [Google Scholar] [CrossRef]
- Frampton, P.H.; Ludwick, K.J. Seeking evolution of dark energy. Eur. Phys. J. 2011, C71. [Google Scholar] [CrossRef]
- Granda, L.N.; Loaiza, E. Big Rip and Little Rip solutions in scalar model with kinetic and Gauss Bonnet couplings. Int. J. Mod. Phys. 2012, D2. [Google Scholar] [CrossRef]
- Capozziello, S.; de Laurentis, M.; Nojiri, S.; Odintsov, S.D. Classifying and avoiding singularities in the alternative gravity dark energy models. Phys. Rev. 2009, D79. [Google Scholar] [CrossRef]
- Frampton, P.H.; Ludwick, K.J.; Scherrer, R.J. Pseudo-rip: Cosmological models intermediate between the cosmological constant and the little rip. Phys. Rev. 2012, D85, 083001:1–083001:5. [Google Scholar] [CrossRef]
- Feng, B.; Wang, X.-L.; Zhang, X.-M. Dark energy constraints from the cosmic age and supernova. Phys. Lett. 2005, B607, 35–41. [Google Scholar]
- Elizalde, E.; Nojiri, S.; Odintsov, S.D. Late-time cosmology in (phantom) scalar-tensor theory: Dark energy and the cosmic speed-up. Phys. Rev. 2004, D70. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Saridakis, E.N.; Setare, M.R.; Xia, J.-Q. Quintom cosmology: Theoretical implications and observations. Phys. Rep. 2010, 493, 1–60. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unifying phantom inflation with late-time acceleration: Scalar phantom-non-phantom transition model and generalized holographic dark energy. Gen. Relativ. Gravit. 2006, 38, 1285–1304. [Google Scholar] [CrossRef]
- Chimento, L.P.; Forte, M.I.; Lazkoz, R.; Richarte, M.G. Internal space structure generalization of the quintom cosmological scenario. Phys. Rev. 2009, D 79. [Google Scholar] [CrossRef]
- Nesseris, S.; Perivolaropoulos, L. Crossing the phantom divide: Theoretical implications and observational status. J. Cosmol. Astropart. Phys. 2007, 0701. [Google Scholar] [CrossRef]
- Capozziello, S.; Nojiri, S.; Odintsov, S.D. Unified phantom cosmology: Inflation, dark energy and dark matter under the same standard. Phys. Lett. 2006, B632, 597–604. [Google Scholar] [CrossRef]
- Vikman, A. Can dark energy evolve to the phantom? Phys. Rev. 2005, D71. [Google Scholar] [CrossRef]
- Xia, J.-Q.; Cai, Y.-F.; Qiu, T.-T.; Zhao, G.-B.; Zhang, X. Constraints on the sound speed of dynamical dark energy. Int. J. Mod. Phys. 2008, D17, 1229–1243. [Google Scholar] [CrossRef]
- Caldwell, R.R. A phantom menace? Phys. Lett. 2002, B545, 23–29. [Google Scholar] [CrossRef]
- Amanullah, R.; Lidman, C.; Rubin, D.; Aldering, G.; Astier, P.; Barbary, K.; Burns, M.S.; Conley, A.; Dawson, K.S.; Deustua, S.E.; et al. Spectra and light curves of six type Ia supernovae at 0.511 < z < 1.12 and the union2 compilation. Astrophys. J. 2010, 716, 712–738. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ito, Y.; Nojiri, S.; Odintsov, S.D. Stability of Accelerating Cosmology in Two Scalar-Tensor Theory: Little Rip versus de Sitter. Entropy 2012, 14, 1578-1605. https://doi.org/10.3390/e14081578
Ito Y, Nojiri S, Odintsov SD. Stability of Accelerating Cosmology in Two Scalar-Tensor Theory: Little Rip versus de Sitter. Entropy. 2012; 14(8):1578-1605. https://doi.org/10.3390/e14081578
Chicago/Turabian StyleIto, Yusaku, Shin’ichi Nojiri, and Sergei D. Odintsov. 2012. "Stability of Accelerating Cosmology in Two Scalar-Tensor Theory: Little Rip versus de Sitter" Entropy 14, no. 8: 1578-1605. https://doi.org/10.3390/e14081578
APA StyleIto, Y., Nojiri, S., & Odintsov, S. D. (2012). Stability of Accelerating Cosmology in Two Scalar-Tensor Theory: Little Rip versus de Sitter. Entropy, 14(8), 1578-1605. https://doi.org/10.3390/e14081578





