Energy, Entropy and Exergy in Communication Networks
Abstract
:1. Introduction
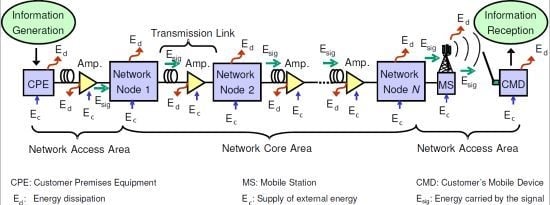
2. Analogies between Communication and Thermodynamic Systems

2.1. An Optical Amplifier As the Carnot Heat Engine



2.2. Data Processing Systems As a Carnot Heat Engine

3. Exergy in Communication Networks
3.1. Exergy-Based Lifecycle Analysis (E-LCA) of ICT Equipment
| Smartphone | Tablet PC | ||||
|---|---|---|---|---|---|
| Material | Mass [g] | Mass [%] | Material | Mass [g] | Mass [%] |
| Glass | 40.9 | 30 | Glass | 140 | 23 |
| Stainless Steel | 38.7 | 29 | Stainless Steel | 115 | 19 |
| Battery | 24.7 | 18 | Battery | 131 | 21 |
| Circuit boards | 15.4 | 11 | Circuit boards | 40 | 7 |
| Display | 7.2 | 5 | Display | 142 | 23 |
| Plastic | 3.1 | 2 | Plastic | 19 | 3 |
| Other materials | 5 | 4 | Other materials | 26 | 4 |
| Total | 135 | 100 | Total | 613 | 100 |
| Category | Value | Unit | Notes |
|---|---|---|---|
| Embodied exergy in materials (cumulative exergy cost (CExC)) | |||
| Aluminum | 341.5 | MJ/kg | using the Bayer process and Hall Cell, 50% bauxite ore |
| Steel | 52.1 | MJ/kg | 50% from scrap, electrolytic process |
| Copper | 67 | MJ/kg | includes mining, concentrating, smelting and refining |
| Iron | 51.04 | MJ/kg | iron casting |
| Zinc | 198.9 | MJ/kg | froth flotation, electrowinning and electrolysis |
| Plastic | 92.3 | MJ/kg | low-density polyethylene (LDPE) from crude oil |
| Other | 20 | MJ/kg | order-of-magnitude estimate |
| Specific exergy consumption of various manufacturing processes | |||
| Metals | 0.28 | kJ/kg | machining process |
| Plastic | 14.9 | kJ/kg | injection, modeling |
| Printed Circuit Boards (PCBs) | 238.4 | MJ/m | FR-4, per area |
| Integrated Circuits (ICs) | 12.5 | MJ/IC | for an average IC size |
| Complex Processor | 1,242 | MJ/processor | including purification of silicon |
| Exergy consumption of different transportation modes | |||
| Air | 22.14 | kJ/kg-km | per km and kg of transported goods |
| Truck | 2.096 | kJ/kg-km | per km and kg of transported goods |
| Rail | 0.253 | kJ/kg-km | per km and kg of transported goods |
| Ship | 0.296 | kJ/kg-km | per km and kg of transported goods |
| Energy source mix for Austria [46] and exergy efficiencies of different electricity generation systems [38] | |||
| Hydroelectric power generation | 57.1 | % | exergy efficiency 90% |
| Coal-Fired Power Plant | 37.2 | % | exergy efficiency 36% |
| Wind Turbine System | 4.2 | % | exergy efficiency 88.5% |
| Solar Photovoltaic System | 1.5 | % | exergy efficiency 25% |
3.2. E-LCA of Radio Access Networks

| E-LCA model | Assumptions for the case with 40% material reutilization |
|---|---|
| Raw Material Extraction | Spatial context: southeast Asia/China Material supply: within the radius of 1,000 km 40% of material flows from the recycling phase |
| Material Transportation | Spatial context: within the radius of 5,000 km Mode of transportation: rail/truck |
| Manufacturing and Assembly | Spatial context: southeast Asia/China |
| Product Transportation | From southeast Asia/China to Austria/Vienna Mode of transportation: rail/truck/ship |
| Operation (Network Design Parameters) | Lifespan: 9 years Area coverage: 95% Backhaul: 95% radio link, 4% fiber, 1% copper Cell diameter: 300 m–500 m Cell type: macro No. of sectors: − 1 sector: 2% − 3 sectors: 97% − 4 sectors: 1% No. of network operators: 3 No. of sites (estimated/actual): 2,385/2,571 |
| End-of-Life Transportation | From northeast Austria/Vienna to southeast Asia/China Mode of transportation:rail/truck/ship |
| Recycling | Based on the mass of equipment Approximately 520 kJ/kg exergy consumption [7] |

4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Aleksic, S. Energy efficiency of electronic and optical network elements. (invited). IEEE J. Sel. Top. Quantum Electron. 2011, 17, 296–308. [Google Scholar] [CrossRef]
- Tzanakaki, A.; Katrinis, K.; Politi, T.; Stavdas, A.; Pikavet, M.; van Daele, P.; Simeonidou, D.; O’ Mahony, M.J.; Aleksic, S.; Wosinska, L.; Monti, P. Dimensioning the future pan-european optical network with energy efficiency considerations. IEEE/OSA JOCN 2011, 3, 272–280. [Google Scholar] [CrossRef]
- Aleksic, S. Power consumption issues in future high-performance switches and routers (invited). Proc. ICTON 2008 2008, 194–198. [Google Scholar]
- Van Heddeghem, W.; Deruyck, M.; Puype, B.; Lannoo, B.; Joseph, W.; Colle, D.; Martens, L.; Demeester, P. Power consumption in telecommunication networks: Overview and reduction strategies. IEEE Comm. Mag. 2011, 49, 62–69. [Google Scholar]
- Fiorani, M.; Casoni, M.; Aleksic, S. Performance and power consumption analysis of a hybrid optical core node. IEEE/OSA JOCN 2011, 3, 502–513. [Google Scholar] [CrossRef]
- WWTF Outline for the first global IT strategy for CO2 reduction. WWTF report 2008.
- Aleksic, S. Energy-Efficient Communication Networks for Improved Global Energy Productivity (invited). Springer Telecommun. Syst. 2013, 1–18. [Google Scholar]
- Clausius, R. Über die bewegende Kraft der Wärme, Part I, Part II. Ann. Phys. 1851, 79, 368–397. [Google Scholar]
- Annila, A. The 2nd law of thermodynamics delineates dispersal of energy. Int. Rev. Phys. 2010, 4, 29–34. [Google Scholar]
- Karnani, M.; Pääkkönen, K.; Annila, A. The physical character of information. Proc. R. Soc. A 2009, 465, 2155–2175. [Google Scholar] [CrossRef]
- Boltzmann, L.; Bush, S.G. The Second Law of Thermodynamics. Theoretical Physics and Philosophical Problems; Reidel: Boston, MA, USA, 1974; (Original work published 1886). [Google Scholar]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Champaign, IL, USA, 1949; ISBN 0-252-72548-4. [Google Scholar]
- El Haj Assad, M. Entropy generation analysis in a slab with non-uniform heat generation subjected to convection cooling. Int. J. Exergy 2011, 9, 355–369. [Google Scholar] [CrossRef]
- El Haj Assad, M.; Brown, D.C. Thermodynamic analysis of end-pumped fiber lasers subjected to surface cooling. IEEE J. Quantum Electron. 2013, 49, 100–107. [Google Scholar] [CrossRef]
- Aleksic, S. Energy and entropy flow in erbium doped fiber amplifiers: A thermodynamic approach. J. Light. Technol. 2012, 30, 2832–2838. [Google Scholar] [CrossRef]
- Djordjevic, I.B.; Xu, L.; Wang, T. Statistical physics inspired energy-efficient coded-modulation for optical communications. Opt. Lett. 2012, 37, 1340–1342. [Google Scholar] [CrossRef] [PubMed]
- Carnot, S. Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance. Annales scientifiques de l’École Normale Supérieure. 1872, 2, 393–457. [Google Scholar]
- Kostic, M. Revisiting The Second Law of Energy Degradation and Entropy Generation: From Sadi Carnot’s Ingenious Reasoning to Holistic Generalization. In Proceedings of the Second Law of Thermodynamics: Status and Challenges Symposium in AIP Conference Proceeding 1411, San Diego, CA, USA, 2011; Volume 327, pp. 327–350.
- Landsberg, P.T.; Evans, D.A. Thermodynamic limits for some light-propagating devices. Phys. Rev. 1968, 166, 242–246. [Google Scholar] [CrossRef]
- Landau, L.D. On the thermodynamics of photoluminescence. J. Phys. (Moscow), USSR 1946, 10, 503–506. [Google Scholar]
- Weinstein, M.A. Thermodynamic limitation on the conversion of heat into light. J. Opt. Soc. Am. A 1960, 50, 597–602. [Google Scholar] [CrossRef]
- Landsberg, P.T.; Tonge, G. Thermodynamic energy conversion efficiencies. J. Appl. Phy. 1980, 51, R1–R20. [Google Scholar] [CrossRef]
- Graf, Th.; Balmer, J.E.; Weber, H.P. Entropy balance of optically pumped CW lasers. Opt. Commun. 1998, 148, 256–260. [Google Scholar] [CrossRef]
- Payen de la Garanderie, P.H. L’extinction thermique de la luminescence comme consequence des deux principes de la thermodynamique. C. R. Acad. Sci. 1965, 260, 3345–3347. [Google Scholar]
- Pastrnak, J.; Hejda, B. Thermodynamical considerations on the quantum efficiency of anti-stokes co-operative luminescence. J. Lumin. 1974, 9, 249–256. [Google Scholar] [CrossRef]
- Levine, D.; Kafri, O. Thermodynamic efficiency of a finite gain laser. Chern. Phys. 1975, 8, 426–431. [Google Scholar] [CrossRef]
- Mungan, C.E.; Gosnell, T.R. Laser cooling of solids. Adv. At. Mol. Opt. Phys. 1999, 40, 161–228. [Google Scholar]
- Knox, R.S.; Parson, W.W. Entropy production and the Second Law in photosynthesis. Biochim. Biophys. Acta 2007, 1767, 1189–1193. [Google Scholar] [CrossRef] [PubMed]
- Jennings, R.J.; Engelmann, E.; Garlaschi, F.; Casazza, A.P.; Zucchelli, G. Photosynthesis and negative entropy production. Biochim. Biophys. Acta 2005, 1709, 251–255. [Google Scholar] [CrossRef] [PubMed]
- Geusic, J.E.; Schulz-DuBois, E.O.; Scovil, H.E.D. Quantum equivalent of the carnot cycle. Phys. Rev. 1967, 156, 343–351. [Google Scholar] [CrossRef]
- Giles, C.R.; Desurvire, E. Modeling erbium-doped fiber amplifiers. IEEE J. Light. Technol. 1991, 9, 271–283. [Google Scholar] [CrossRef]
- Becker, P.C.; Olsson, N.A.; Simpson, J.R. Erbium-Doped Fiber Amplifiers: Fundamentals and Technology; Academic Press: Waltham, MA, USA, 1999. [Google Scholar]
- Parker, M.C.; Walker, S.D. Differential temperature Carnot heat analysis shows that computing machines are thermodynamically irreversible. Opt. Commun. 2008, 281, 3440–3446. [Google Scholar] [CrossRef]
- Landauer, R. Minimum energy requirements in communication. Science 1996, 272, 1914–1918. [Google Scholar] [CrossRef] [PubMed]
- Socolow, R.H.; Rochli, G.I. Efficient Use of Energy, a Physics Perspective; American Institute of Physics (AIP): Spring Branch, TX, USA, 1975; p. 305. [Google Scholar]
- Gutowski, T.; Dahmus, J.; Thiriez, A.; Branham, M.; Jones, A. A Thermodynamic Characterization of Manufacturing Processes. In Proceedings of the IEEE International Symposium on Electronics and the Environment, Orlando, FL, USA, 7–10 May 2007; pp. 1–6.
- Masini, A.; Ayres, R.U. An Application of Exergy Accounting to Four Basic Metal Industries; CMER, INSEAD: Fontainebleau, France, 1996; pp. 1–51. [Google Scholar]
- Rosen, M.A.; Bulucea, C.A. Using exergy to understand and improve the efficiency of electrical power technologies. Entropy 2009, 11, 820–835. [Google Scholar] [CrossRef]
- Aleksic, S.; Safaei, M. Exergy based analysis of radio access networks (invited). to be published in Proceedings of ICEAA - IEEE APWC - EMS 2013, 2013; 1–8. [Google Scholar]
- Scharnhorst, W. Life Cycle Assessment of Mobile Telephone Networks with Focus on the End-of-Life Phase. Ph.D. Thesis, EPFL, Lausanne, 2006; pp. 1–182. [Google Scholar]
- Hannemann, C.R.; Carey, V.P.; Shah, A.J. Lifetime Exergy Consumption as a Sustainability Metric for Enterprise Servers. In Proceedings of ASME Int. Conference on Energy Sustainability, Jacksonville, FL, USA, 10-14 August 2008. ASME ES2008–54181.
- Apple, Apple and Environment-Product Environmental Reports. 2012. Available online: http://www.apple.com/environment/reports/ (accessed on 5 May 2013).
- Ginley, D.S.; Cahen, D. Fundamentals of Materials for Energy and Environmental Sustainability; Cambridge University Press: Cambridge, UK, 2011; p. 772. [Google Scholar]
- Mahadevan, P.; Shah, A.; Bash, C. Reducing Lifecycle Energy Use of Network Switches. In Proceedings of ISSST, Arlington, VA, USA, 17–19 May 2010; pp. 1–6.
- Safaei, M. Exergy-Based Life Cycle Assessment (E-LCA) of Cloud Computing. Master Thesis, Vienna University of Techonolgy, Vienna, Austria, 2013; p. 92. [Google Scholar]
- Bittermann, W.; Mayer, B. Energie in Oesterreich Energiebilanzen 2010. Statistik Austria. 2011. Available online: http://www.statistik.at textcolorred (accessed on25 May 2013).
- Statistics Austria Demographic indices. 2012. Available online: http://www.statistik.at/web_en/statistics/population/demographic_indices/index.html (accessed on 10 May 2013).
- Aleksic, S.; Deruyck, M.; Vereecken, W.; Joseph, W.; Pickavet, M.; Martens, L. Energy efficiency of femtocell deployment in combined wireless/optical access networks. Elsevier Comput. Netw. 2013, 57, 1217–1233. [Google Scholar] [CrossRef] [Green Version]
- Aleksic, S.; Franzl, G.; Bogner, T.; Mair am Tinkhof, O. Framework for Evaluating Energy Efficiency of Access Networks. In Proceedings of IEEE ICC’13-GBA, Budapest, Hungary, 13 June 2013; pp. 1–6.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aleksic, S. Energy, Entropy and Exergy in Communication Networks. Entropy 2013, 15, 4484-4503. https://doi.org/10.3390/e15104484
Aleksic S. Energy, Entropy and Exergy in Communication Networks. Entropy. 2013; 15(10):4484-4503. https://doi.org/10.3390/e15104484
Chicago/Turabian StyleAleksic, Slavisa. 2013. "Energy, Entropy and Exergy in Communication Networks" Entropy 15, no. 10: 4484-4503. https://doi.org/10.3390/e15104484
APA StyleAleksic, S. (2013). Energy, Entropy and Exergy in Communication Networks. Entropy, 15(10), 4484-4503. https://doi.org/10.3390/e15104484