An Automatic Multilevel Image Thresholding Using Relative Entropy and Meta-Heuristic Algorithms

Abstract

Multilevel thresholding has been long considered as one of the most popular techniques for image segmentation. Multilevel thresholding outputs a gray scale image in which more details from the original picture can be kept, while binary thresholding can only analyze the image in two colors, usually black and white. However, two major existing problems with the multilevel thresholding technique are: it is a time consuming approach, i.e., finding appropriate threshold values could take an exceptionally long computation time; and defining a proper number of thresholds or levels that will keep most of the relevant details from the original image is a difficult task. In this study a new evaluation function based on the Kullback-Leibler information distance, also known as relative entropy, is proposed. The property of this new function can help determine the number of thresholds automatically. To offset the expensive computational effort by traditional exhaustive search methods, this study establishes a procedure that combines the relative entropy and meta-heuristics. From the experiments performed in this study, the proposed procedure not only provides good segmentation results when compared with a well known technique such as Otsu’s method, but also constitutes a very efficient approach.

1. Introduction

Segmenting an image into its constituents is a process known as thresholding [1,2]. Those constituents are usually divided into two classes: foreground (significant part of the image), and background (less significant part of the image). Several methods for thresholding an image have been developed over the last decades, some of them based on entropy, within and between group variance, difference between original and output images, clustering, etc. [3,4,5].

The process of thresholding is considered as the simplest image segmentation method, which is true when the objective is to convert a gray scale image into a binary (black and white) one (that is to say only one threshold is considered). However, in the process of segmentation, information from the original image will be lost if the threshold value is not adequate. This problem may even deteriorate as more than one threshold is considered (i.e., multilevel thresholding) since not only a proper number of thresholds is desirable, but also a fast estimation of their values is essential [1].

It has been proven over the years that as more thresholds are considered in a given image, the computational complexity of determining proper values for each threshold increases exponentially (when all possible combinations are considered). Consequently, this is a perfect scenario for implementing meta-heuristic tools [6] in order to speed up the computation and determine proper values for each threshold.

When dealing with multilevel thresholding, in addition to the fast estimation, defining an adequate number of levels (thresholds that will successfully segment the image into several regions of interest from the background), has been another problem without a satisfactory solution [7]. Therefore, the purpose and main contribution of this study is to further test the approach proposed in [8] which determines the number of thresholds necessary for segmenting a gray scaled image automatically. The aforementioned is achieved by optimizing a mathematical model based on the Relative Entropy Criterion (REC).

The major differences between this work and the one presented in [8], are that a more extensive and comprehensive testing of the proposed method was carried out. To verify the feasibility of the proposed model and reduce the computational burden, when carrying out the optimization process, this study implements three meta-heuristic tools and compares the output images with that delivered by a widely known segmentation technique named Otsu’s method. In addition to the aforementioned, further tests with images having low contrast and random noise are conducted; this intends to probe the robustness, effectiveness and efficiency of the proposed approach.

The following paper is organized as follows: Section 2 introduces the proposed procedure, which consists of the mathematical model based on the relative entropy and the meta-heuristics—virus optimization algorithm, genetic algorithm, and particle swarm optimization as the solution searching techniques. Section 3 illustrates the performance of the proposed method when the optimization is carried out by three different algorithms VOA, GA and PSO, where six different types of images were tested. Lastly, some concluding remarks and future directions for research are provided in Section 4.

2. The Proposed Multilevel Thresholding Method

A detailed explanation of the proposed method is given in this section, where the mathematical formulation of the model is presented and the optimization techniques are introduced.

2.1. Kullback-Leibler Information Distance (Relative Entropy)

The Kullback-Leibler information distance (known as Relative Entropy Criterion) [9] between the true and the fitted probabilities is implemented in [8] for estimating an appropriate model that will best represent the histogram coming from the gray level intensity of an image. According to McLachlan and Peel [10] this information distance is defined as in Equation (1). However, the gray levels (intensity) are discrete values between [0, 255]; therefore, Equation (1) can be rewritten as in Equation (2):

$$J\left(d\right)=I\left\{p\left(i\right);p\left(i;{\theta }_d\right)\right\}={\displaystyle \int \left(p\left(i\right){\log }_e\left[\frac{p\left(i\right)}{p\left(i;{\theta }_d\right)}\right]\right)di}$$

(1)

$$J\left(d\right)=I\left\{p\left(i\right);p\left(i;{\theta }_d\right)\right\}={\displaystyle \sum _{i=0}^{255}\left(p\left(i\right){\log }_e\left[\frac{p\left(i\right)}{p\left(i;{\theta }_d\right)}\right]\right)}$$

(2)

where p(i) and p(i;θ_d) are the probabilities values from the image histogram and fitted model respectively. These probabilities are estimated using Equations (3) and (4), where the value of $i\in \left[0, 255\right]$ and represents the gray intensity of a pixel at location (x, y) on the image of size $M\times N$ pixels; while ${\displaystyle {\sum }_{j=1}^{d}g\left(i,{\theta }_j\right)}$ in Equation (4) is a mixture of “d” distributions which are used to estimate the value of p(i;θ_d). Lastly, θ_j is a vector containing the parameters of each distribution in the mixture:

$$p\left(i\right)=\frac{Total number of pixels with gray intesity of i}{Size of the image}$$

(3)

$$p\left(i;{\theta }_d\right)=g\left(i,{\theta }_1\right)+\cdots +g\left(i,{\theta }_d\right)={\displaystyle \sum _{j=1}^{d}g\left(i,{\theta }_j\right)}$$

(4)

In this study Gaussian distributions are used to estimate Equation (4), where the central limit theorem (C.L.T.) is the motivation of using this type of distributions [11]. Therefore, Equation (4) can be expressed as in Equation (5):

$$p\left(i;{\theta }_d\right)={\displaystyle \sum _{j=1}^d\left(\frac{w_j}{\sqrt{2\pi }{\sigma }_j}{e}^{-\frac{1}{2}\left[{\left(\frac{i-{\mu }_j}{{\sigma }_j}\right)}^2\right]}\right)}$$

(5)

where θ_j contains the prior probability (or weight) w_j, mean μ_j, and variance σ²_j, of the j^th Gaussian distribution. The minimization of the Relative Entropy Criterion function can be interpreted as the distance reduction between the observed and estimated probabilities. This should provide a good description of the observed probabilities p(i) given by the gray level histogram of the image under study. However, finding an appropriate number of distributions, i.e., “d”, is a very difficult task [12,13,14,15]. Consequently, the addition of a new term in Equation (2), which is detailed in the following subsection helps to automatically determine a suitable amount of distributions.

2.2. Assessing the Number of Distributions in a Mixture Model

The purpose of assuming a mixture of “d” distributions in order to estimate p(i;θ_d) in the REC function, is that the number of thresholds for segmenting a given image, can be easily estimated using Equation (6). The value of each threshold is the gray level intensity “i” that minimizes Equation (7), where “i” is a discrete unit (i.e., an integer $\in$ [0, 255]):

$$number of thresholds=d-1$$

(6)

$$Threshol{d}_k=\arg \underset{i}{\min }\left\{\left|p\left(i;{\theta }_k\right)-p\left(i;{\theta }_{k+1}\right)\right|\right\}k=1,2,\mathrm{...},d-1$$

(7)

Given that estimating a suitable number of distributions “d” is a very difficult task, the method proposed in [8] attempts to automatically assess an appropriate value for “d” combining Equations (2) and (8) as a single objective function. The vector w contains all the prior probabilities (weights) of the mixture model. The values max(w) and min(w) are the maximum and minimum weights in w respectively:

$$P\left(d\right)=\frac{1}{d-1}{\displaystyle \sum _{j=1}^d\left(\frac{\max (w)-w_j}{\max (w)-\min (w)}\right)}$$

(8)

Equation (8) compares each prior probability w_j with respect to the largest one in the vector w. The result is normalized using the range given by [max(w)–min(w)] in order to determine how significant w_j is with respect to the probability that contributes the most in the model, i.e., max(w). Therefore, Equation (8) will determine if the addition of more Gaussian distributions is required for a better estimation of p(i;θ_d). The term $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$d-1$}\right.$ will avoid Equation (8) overpowering Equation (2) when the mathematical model of Equation (9) is minimized:

$$\mathsf{\Theta }\left(d\right)={\displaystyle \sum _{i=0}^{255}\left(p\left(i\right){\log }_e\left[\frac{p\left(i\right)}{p\left(i;{\theta }_d\right)}\right]\right)}+\frac{1}{d-1}{\displaystyle \sum _{j=1}^d\left(\frac{\max (w)-w_j}{\max (w)-\min (w)}\right)}$$

(9)

Therefore, by minimizing Equation (9), the introduced approach will not only determine an appropriate number of distributions in the mixture model, but will also find a good estimation (fitting) of the probabilities p(i) given by the image histogram. An appropriate value for “d” is determined by increasing its value by one, i.e., d^l = d^l−1 + 1 where “l” is the iteration number, and minimizing Equation (9) until a stopping criterion is met and the addition of more distributions to the mixture model is not necessary. Therefore, not all the possible values for “d” are used.

2.3. Mathematical Model Proposed for Segmenting (Thresholding) a Gray Level Image

The mathematical model which is used for segmenting a gray level image is presented as in Equation (10). By minimizing Equation (10) with “d” Gaussian distributions, J(d) is in charge of finding a good estimation (fitting) of the image histogram, while P(d) determines whenever the addition of more distributions to the model is necessary:

$$Min\mathsf{\Theta }\left(d\right)=Min\left[J\left(d\right)+P\left(d\right)\right]\underset{{\theta }_d,d}{=Min}\left[{\displaystyle \sum _{i=0}^{255}\left(p\left(i\right){\log }_e\left[\frac{p\left(i\right)}{p\left(i;{\theta }_d\right)}\right]\right)}+\frac{1}{d-1}{\displaystyle \sum _{j=1}^d\left(\frac{\max (w)-w_j}{\max (w)-\min (w)}\right)}\right]$$

(10)

subject to:

$${\displaystyle \sum _{j=1}^d{w}_j}=1$$

(11)

$$w_j>0\forall j\in \left[1,d\right]$$

(12)

$${\sigma }_j^2>0\forall j\in \left[1,d\right]$$

(13)

Equation (11) guarantees a summation of the prior probabilities equal to 1, while Equations (12) and (13) ensure positive values to all prior probabilities and variances in the mixture model, respectively. To minimize Equation (10), a newly developed meta-heuristic named Virus Optimization Algorithm [16], the widely known Genetic Algorithm [17] and Particle Swarm Optimization algorithm [18] are implemented in this study.

The flowchart at Figure 1 details the procedure of the proposed method using VOA (the similar idea is also applied to GA and PSO). As can be observed, the optimization tool (VOA, GA, or PSO) will optimize Equation (10) with d^l Gaussian distributions until the stopping criterion of the meta-heuristic is reached. Once the algorithm finishes optimizing Equation (10) with d^l distributions, the proposed method decides if the addition of more components is necessary if and only if Θ(d^l) ≥ Θ(d^l−1) is true; otherwise a suitable number of distributions (thresholds) just been found and the results coming from Θ(d^l−1) are output.

The purpose of using three algorithmic tools, is not only to reduce the computation time when implementing the proposed approach, but also, to verify if the adequate number of thresholds suggested by optimizing Equation (10) with different optimization algorithm remains the same. The reason of the aforementioned is because different algorithms may reach different objective function values. However, if the proposed method (Figure 1) is robust enough, all algorithms are expected to stop iterating when reaching a suitable number of thresholds, and this number has to be the same for all the optimization algorithms.

2.4. Algorithmic Optimization Tools

2.4.1. Virus Optimization Algorithm (VOA)

Inspired from the behavior of a virus attacking a host cell, VOA [8,16] is a population-based method that begins the search with a small number of viruses (solutions). For continuous optimization problems, a host cell represents the entire multidimensional solution space, where the cell’s nucleolus denotes the global optimum. Virus replication indicates the generation of new solutions while new viruses represent those created from the strong and common viruses.

The strong and common viruses are determined by the objective function value of each member in the population of viruses, i.e., the better the objective function value of a member the higher the chance to be considered as strong virus. The number of strong viruses is determined by the user of the algorithm, which we recommend to be a small portion of the whole population (strong and common).

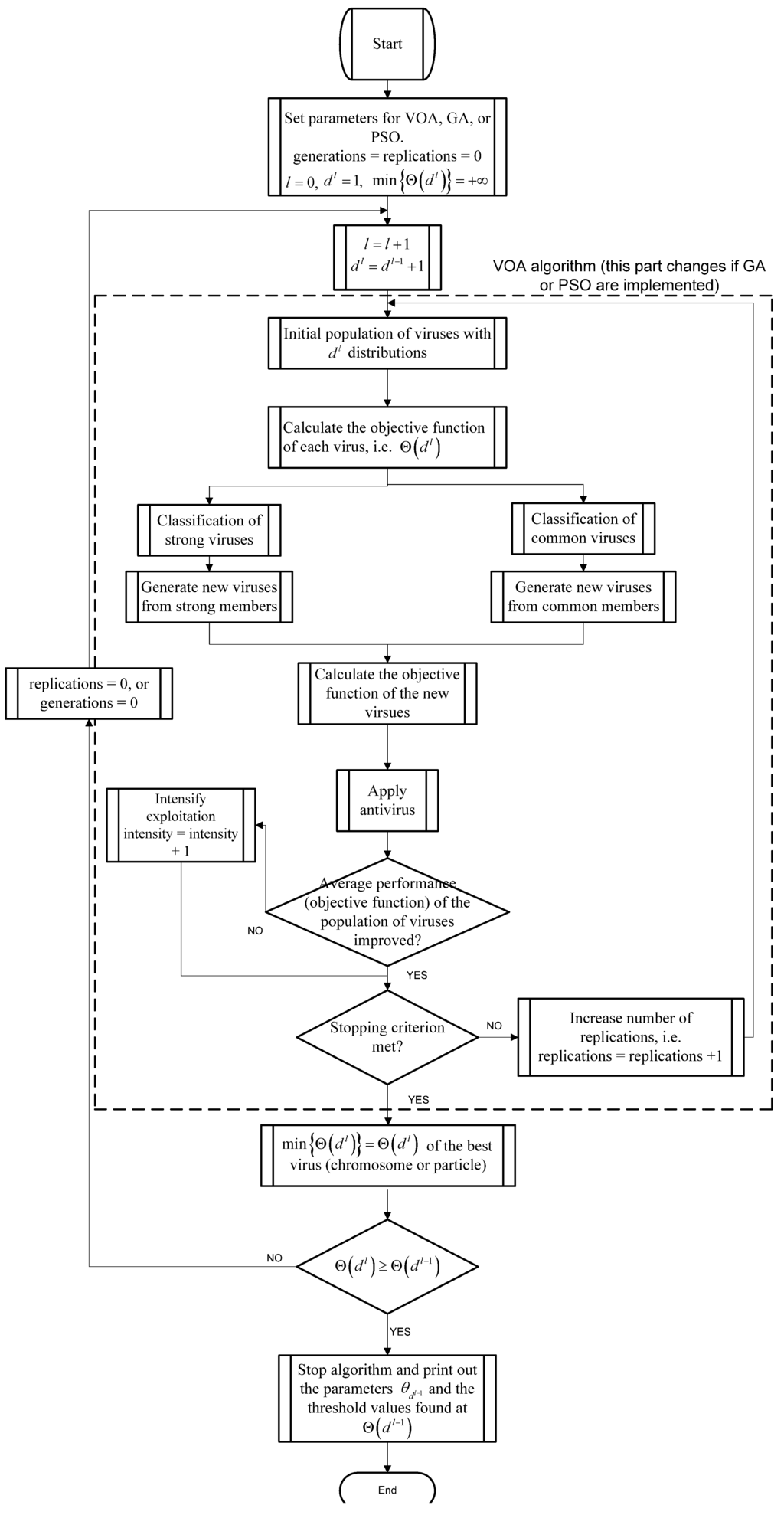
Figure 1. Flowchart of the proposed optimization procedure.

Figure 1. Flowchart of the proposed optimization procedure.

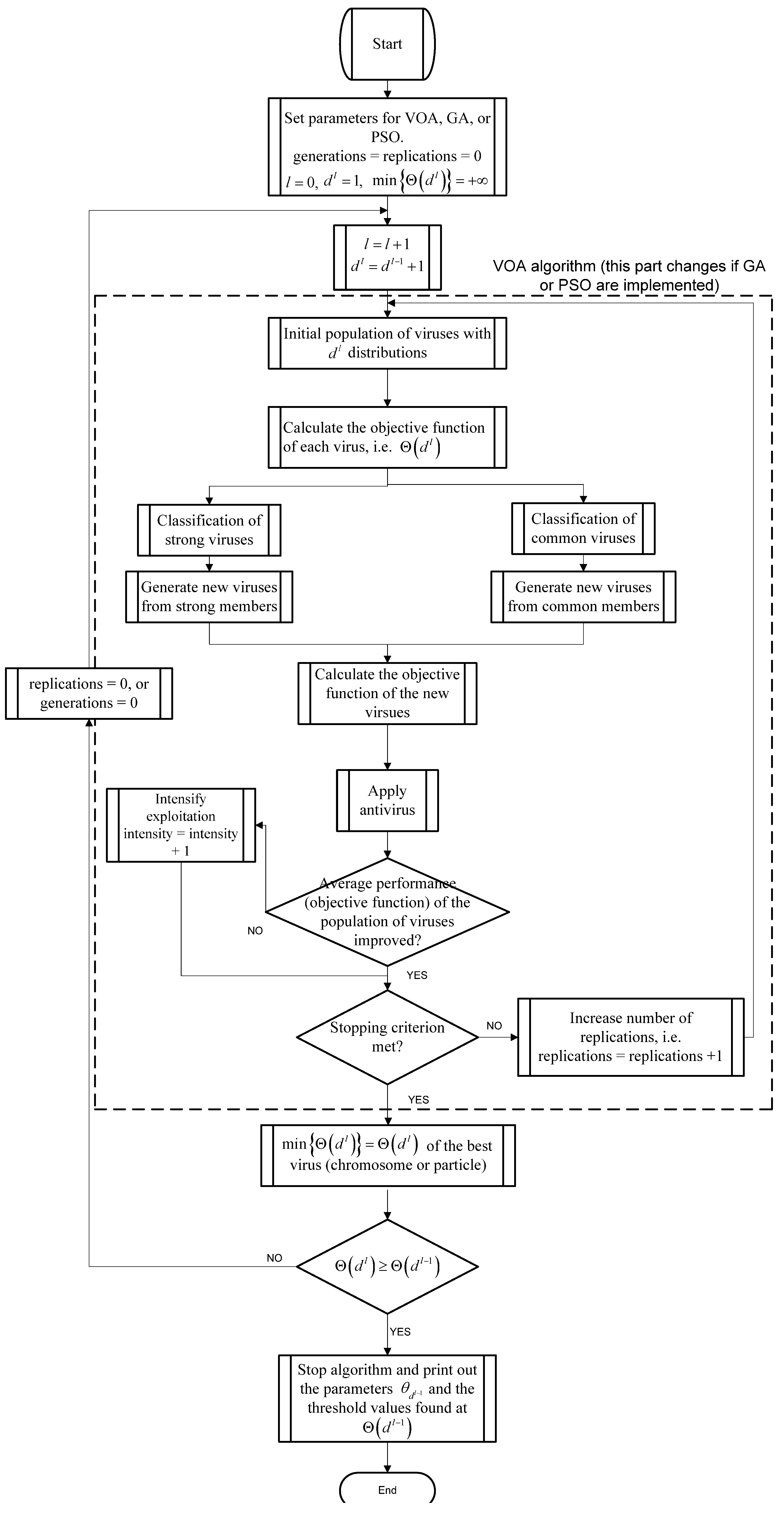
To simulate the replication process when new viruses are created, the population size will grow after one complete iteration. This phenomenon is controlled by the antivirus mechanism that is responsible for protecting the host cell against the virus attack. The whole process will be terminated based on the stopping criterion: the maximum number of iterations (i.e., virus replication), or the discovery of the global optimum (i.e., cell death is achieved).

The VOA consists of three main processes: Initialization, Replication, and Updating/Maintenance. The Initialization process uses the values of each parameter (defined by the user) to create the first population of viruses. These viruses are ranked (sorted) based on the objective function evaluation Θ(d) to select strong and common members. Here the number of strong members in the population of viruses is a parameter to be defined by the user, without considering the strong members; the population of viruses is the number of common viruses.

The replication process is performed using the parameters defined by the user in the Initialization stage described above, where a temporary matrix (larger than the matrix containing the original viruses) will hold the newly-generated members. Here, Equations (14) and (15) are used to generate new members, where “vn” stands for the value of the variable in the n^th dimensional space, for viruses in the previous replication. “svn” stands for the value of the variable in the n^th dimensional space generated from the strong viruses in the current replication, and “cvn” is the value of the variable in the n^th dimensional space generated from the common viruses in the current replication:

$$svn=vn\pm \left(\raisebox{1ex}{$rand()$}\!\left/ \!\raisebox{-1ex}{$\text{intensity}$}\right.\right)\times vn$$

(14)

$$cvn=vn\pm rand()\times vn$$

(15)

The intensity in Equation (14) above reduces the random perturbation that creates new viruses from the strong members. This will allow VOA to intensify exploitation in regions more likely to have a global optimum (i.e., areas where the strong viruses are located). The initial value for the intensity is set as one, which means that the random perturbation for strong and common viruses is the same in the early stages. Therefore, the exploration power of VOA is expected to be enhanced during the program’s early stages. The intensity value increases by one when the average performance of the population of viruses in VOA; that is to say, the average objective function value of the whole population of viruses, did not improve after a replication. The flowchart of the proposed procedure is illustrated in Figure 1. Note that the VOA part can be easily switched to other optimization algorithms such as GA and PSO.

2.4.2. Genetic Algorithm (GA)

The basic concept of Genetic Algorithms or GAs [17] is to simulate processes in natural systems, necessary for evolution, especially those that follows the principles first laid down by Charles Darwin of survival of the fittest. In GA a portion of existing population (solutions) is selected to breed a new population (new solutions), individuals are selected to reproduce (crossover) through a fitness-based process (objective function). Mutation takes place when new individuals are created after crossover to maintain a diverse population through generations. The standard GA is summarized in Figure 2, for the selection of the parents the roulette wheel is used in this study, as for the population maintenance mechanism the best members in the pooled population (parents and offspring) survive. The crossover operators implemented in this paper are the geometric and arithmetic means [Equations (16) and (17)] for the creation of the first and second child respectively. Note that only the integer part is taken by the program since the chromosome contains only integers. The mutation operator in GA uses Equation (18), which is the floor function of a random number generated between [T_i−1, T_i] where T₀ = 0 and T_d = 255:

$${T_i}^{child1}=\raisebox{1ex}{$\left({T_i}^{parent1}+{T_i}^{parent2}\right)$}\!\left/ \!\raisebox{-1ex}{$2$}\right.,i\in \left[1,2,\cdots ,d-1\right]$$

(16)

$${T_i}^{child2}={\left({T_i}^{parent1}\times {T_i}^{parent2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},i\in \left[1,2,\cdots ,d-1\right]$$

(17)

$$T_i=\lfloor rand\left[\left(T_{i-1}+1\right),\left(T_i-1\right)\right]\rfloor ,i\in \left[1,2,\cdots ,d\right]$$

(18)

Figure 2. Genetic Algorithm (GA) overview.

Figure 2. Genetic Algorithm (GA) overview.

2.4.3. Particle Swarm Optimization (PSO)

Particle Swarm Optimization was inspired by social behavior of bird flocking or fish schooling [18]. Each candidate solution (known as particle) keeps track of its coordinates in the problem space which are associated with the best solution (fitness) it has achieved so far, also known as the particle’s best (pbest). The swarm on the other hand, also keeps track of the best value, obtained until now, by any particle in the neighbor of particles. This is known as the global best (gbest). The basic concept of PSO consists of changing the velocity of each particle towards the gbest and pbest location. This velocity is weighted by a random term, with separated random numbers being generated for acceleration toward the pbest and gbest locations. The standard PSO is summarized as in Figure 3. For this study, the velocity of the particle is bounded to a V_max value which is only 2% of the gray intensity range; that is to say, V_i $\in$ [−V_max , V_max] where V_max = 0.02 × (255 − 0).

Figure 3. Overview of the Particle Swarm Optimization (PSO) algorithm.

Figure 3. Overview of the Particle Swarm Optimization (PSO) algorithm.

The stopping criterion for the VOA (GA or PSO) is when two consecutive replications (generations) did not improve the objective function value of the best virus (chromosome or particle). Once the VOA (GA or PSO) stops searching and the best value for the Θ(d^l) is determined, the proposed method will decide if the addition of more distributions is necessary when the condition Θ(d^l) < Θ(d^l−1) is satisfied; otherwise the proposed method will automatically stop iterating. After the proposed method stops, the parameters contained inside the vector θ_d^l-1 that represents the set of parameters of the best result in the previous iteration are output.

In order to avoid computational effort of calculating the threshold values that minimize Equation (7), the VOA (GA and PSO) will code each threshold value inside each solution, i.e., each virus (chromosome or particle) will have a dimensionality equal to the number of thresholds given by Equation (6). During the optimization, when the search of the best value for Θ(d^l) is in process, each threshold will be treated as a real (not an integer) value, which can be considered as the coded solution of the VOA and PSO.

In the case of GA a chromosome containing integer values is used for encoding the solution. In order to evaluate the objective function of each virus or particle, the real values coded inside each member will be rounded to the nearest integer, whereas in GA this is not necessary since each chromosome is an array of integers. The parameters for each Gaussian distribution are computed as in Equations (19)–(21), which is considered as the decoding procedure of the three meta-heuristics implemented in this study:

$$w_j={\displaystyle \sum _{i=T_{j-1}}^{T_j}}p(i),\forall j\in [1,d]$$

(19)

$${\mu }_j={\displaystyle \sum _{i=T_{j-1}}^{T_j}\left(i\times \frac{p(i)}{w_j}\right),}\forall j\in [1,d]$$

(20)

$${\sigma }_j^2={\displaystyle \sum _{i=T_{j-1}}^{T_j}\left({\left(i-{\mu }_j\right)}^2\times \frac{p(i)}{w_j}\right),}\forall j\in [1,d]$$

(21)

In Equations (19)–(21), T_j represents the j^th threshold in the solution. The values for T₀ = 0 and T_d = 255, which are the lower and upper limits for thresholds values. During the optimization process, special care should be taken when generating new solutions (viruses, offspring, or particles). The details are as follows:

Condition 1: The threshold should be in increasing order when coded inside each solution, and two thresholds cannot have the same value, i.e., T₀ < T₁ < T₂ <...< T_d.

Condition 2: The thresholds are bounded by the maximum (T_d = 255) and minimum (T₀ = 0) intensity in a gray level image, i.e., 0 ≤ T_j ≤ 255, $\forall$ j $\in$ [1, d−1].

Equation (22) is checked to ensure that the first condition is satisfied, where $\forall$ i, j $\in$ [1, d−1] and i < j. If Equation (22) is not satisfied then the solution (virus, chromosome, or particle) is regenerated using Equation (23), where $\lfloor \cdot \rfloor$ is the floor function. The second condition is also checked and whenever any threshold value is outside the boundaries, i.e., T_j $\le$ 0 or T_j $\ge$ 255, the virus (chromosome or particle) is regenerated using Equation (23).

$$T_i-T_j\le 0$$

(22)

$$\begin{array}{l}VOA,PSO:T_i=\left(rand()\times \frac{255}{d}\right)+\left(\left(i-1\right)\times \frac{255}{d}\right)\\ GA:T_i=\lfloor \left(rand()\times \frac{255}{d}\right)+\left(\left(i-1\right)\times \frac{255}{d}\right)\rfloor \end{array}$$

(23)

3. Experimental Results

In order to further test the method proposed in [8], five different types of images were tested. The first image, which has a known number of three thresholds as in this case is tested (Figure 4a); secondly, an image containing text on a wrinkled paper which will cause lighting variation is tested (Figure 5a). Thirdly, the Lena image (Figure 6a) [1,12,13,14,15] is tested, which is considered as a benchmark image when a new thresholding technique is proposed.

Figure 4. Test image 1: (a) Original image; Thresholded image implementing (b) VOA, (c) GA, (d) PSO, and (e) Otsu’s method using three thresholds.

Figure 4. Test image 1: (a) Original image; Thresholded image implementing (b) VOA, (c) GA, (d) PSO, and (e) Otsu’s method using three thresholds.

Figure 5. Test image 2: (a) Original image; Thresholded image implementing (b) VOA, (c) GA, (d) PSO, and (e) Otsu’s method with two thresholds.

Figure 5. Test image 2: (a) Original image; Thresholded image implementing (b) VOA, (c) GA, (d) PSO, and (e) Otsu’s method with two thresholds.

Figure 6. Test image 3: (a) Original image; Thresholded image implementing (b) VOA, (c) GA, (d) PSO, and (e) Otsu’s method with four thresholds. (taken from [1] )

Figure 6. Test image 3: (a) Original image; Thresholded image implementing (b) VOA, (c) GA, (d) PSO, and (e) Otsu’s method with four thresholds. (taken from [1] )

3.1. Algorithmic Setting (VOA, GA, and PSO)

The setting of VOA, GA, and PSO was determined by using Design of Experiments (DoE) [19,20] to know which values for the parameters are suitable when optimizing Equation (10). The full factorial design, i.e., 3-levels factorial design was performed for the four parameters of the VOA; in other words, 3⁴ combinations of the four parameters were tested. Table 1 shows the results after performing DoE, where the final setting of the VOA is presented in bold.

Table 1. Parameter values (factor levels) used during the for the VOA.

Parameter	Low Level	Medium Level	High Level
Initial population of viruses	5	10	30
Viruses considered as strong	1	3	10
Growing rate of strong viruses	2	5	10
Growing rate of common viruses	1	3	6

Table 1. Parameter values (factor levels) used during the for the VOA.

Parameter	Low Level	Medium Level	High Level
Initial population of viruses	5	10	30
Viruses considered as strong	1	3	10
Growing rate of strong viruses	2	5	10
Growing rate of common viruses	1	3	6

Similarly, a 3³ full factorial design was implemented in order to set the population size (ps), crossover and mutation probabilities (pc and pm) respectively for GA. Table 2 summarizes the experimental settings and the final setting (in bold) of the GA. As for PSO a 3⁴ full factorial design determined the values for the swarm size, inertia weight (w), cognitive and social parameters (c1 and c2) respectively. Table 3 summarizes the experimental settings of the PSO algorithm and the final setting is also highlighted in bold.

Table 2. Parameter values (factor levels) used during the DoE for the GA.

Parameter	Low Level	Medium Level	High Level
Population size (ps)	5	10	30
Probability of crossover (pc)	0.8	0.9	0.99
Probability of mutation (pm)	0.05	0.1	0.15

Table 2. Parameter values (factor levels) used during the DoE for the GA.

Parameter	Low Level	Medium Level	High Level
Population size (ps)	5	10	30
Probability of crossover (pc)	0.8	0.9	0.99
Probability of mutation (pm)	0.05	0.1	0.15

Table 3. Parameter values (factor levels) used during the DoE for the PSO.

Parameter	Low Level	Medium Level	High Level
Swarm size	5	10	30
Inertia weight (w)	0.5	0.8	0.99
Cognitive parameter (c1)	2	2.1	2.2
Social parameter (c2)	2	2.1	2.2

Table 3. Parameter values (factor levels) used during the DoE for the PSO.

Parameter	Low Level	Medium Level	High Level
Swarm size	5	10	30
Inertia weight (w)	0.5	0.8	0.99
Cognitive parameter (c1)	2	2.1	2.2
Social parameter (c2)	2	2.1	2.2

The basic idea of the DoE is to run the 3⁴, 3³, and 3⁴, parameters combinations for VOA, GA, and PSO respectively, to later select which level (value) yielded the best performance (lower objective function value). Once the values for each parameter which delivered the best objective function value are identified, each test image is segmented by optimizing Equation (10) with each of the algorithmic tools used in this study.

The advantage of using DoE is that it is a systematic as well as well-known approach when deciding the setting yielding the best possible performance among all the combinations used during the full factorial design. In addition to the aforementioned, it is also a testing method that has been proven to be quite useful in many different areas such as tuning algorithm parameters [20].

3.2. Segmentation Results for the Proposed Model Using Meta-Heuristics as Optimization Tools

A comprehensive study of the proposed model implementing the three meta-heuristics introduced above is detailed in this part of Section 3. Additionally, a well-known segmentation method (Otsu’s) is implemented, where only the output image is observed in order to verify if the segmentation result given by the optimization algorithms used to minimize Equation (10) is as good as the one provided by Otsu’s method. The reason of the above mentioned, is because in terms of CPU time Otsu’s is a kind of exhaustive search approach; therefore, it is unfair to compare both ideas (the proposed approach and the Otsu’s method) in terms of computational effort.

Table 4, Table 5, Table 6, Table 7 and Table 8 detail the performance of the methods used for optimizing Equation (10) over different images. The results (objective function, threshold values, means, variances, and weights) are averaged over 50 independent runs, where the standard deviations of those 50 runs are not shown because they are in the order of 10⁻¹⁷.

By testing the image in Figure 4a it is observed that implementing the three meta-heuristics previously introduced for the optimization of Equation (10), the correct number of thresholds needed for segmenting the image is achieved (which is three). The computational effort and parameters of each Gaussian distribution (${\theta }_j=\left\{w_j,{\mu }_j,{{\sigma }_j}^2\right\}$) are summarized in Table 4. Here, the number of iterations for the algorithms were four, i.e., the proposed method optimized By testing the image in Figure 4a it is observed that implementing the three meta-heuristics previously introduced for the optimization of Equation (10), the correct number of thresholds needed for segmenting the image is achieved (which is 3).

Table 4. Thresholding results over 50 runs for the test image 1.

Algorithm	Number of Thresholds	Objective Function	Threshold Values	Means	Variances	Weights	CPU Time per Iteration (s)	Total CPU Time for the Proposed Approach (s)
VOA	1	2.410	244	66.808	3836.212	0.637	0.026	0.507
				251.391	37.709	0.363
	2	0.976	62, 244	33.209	12.892	0.483	0.071
				175.849	1298.019	0.167
				252.452	0.616	0.350
	3	0.826	44, 145, 246	33.123	11.272	0.480	0.117
				78.128	390.079	0.021
				187.900	186.987	0.149
				252.469	0.482	0.350
	4	0.896	55, 97, 163, 246	33.178	12.123	0.482	0.294
				75.522	119.910	0.017
				128.441	258.119	0.003
				185.922	82.920	0.142
				252.158	6.177	0.356
GA	1	2.410	244	69.838	4226.048	0.650	0.106	0.658
				252.452	0.616	0.350
	2	0.994	65, 242	33.239	13.806	0.483	0.147
				176.018	1256.142	0.166
				252.440	0.736	0.351
	3	0.857	45, 111, 242	33.131	11.350	0.481	0.195
				74.412	187.027	0.019
				186.725	207.543	0.150
				252.440	0.736	0.351
	4	0.882	44, 143, 155, 247	33.123	11.272	0.480	0.211
				77.924	377.966	0.021
				150.013	12.387	0.001
				188.193	191.885	0.149
				252.477	0.431	0.349
PSO	1	2.384	247	70.158	4274.185	0.651	0.083	0.584
				252.477	0.431	0.349
	2	0.955	65, 247	33.239	13.806	0.483	0.118
				176.672	1288.421	0.167
				252.477	0.431	0.349
	3	0.857	45, 111, 242	33.131	11.350	0.481	0.172
				74.412	187.027	0.019
				186.725	207.543	0.150
				252.440	0.736	0.351
	4	0.880	42, 135, 154, 247	33.097	11.070	0.479	0.211
				74.922	381.817	0.022
				144.535	35.001	0.001
				188.161	192.778	0.149
				252.477	0.431	0.349

Table 4. Thresholding results over 50 runs for the test image 1.

Algorithm	Number of Thresholds	Objective Function	Threshold Values	Means	Variances	Weights	CPU Time per Iteration (s)	Total CPU Time for the Proposed Approach (s)
VOA	1	2.410	244	66.808	3836.212	0.637	0.026	0.507
				251.391	37.709	0.363
	2	0.976	62, 244	33.209	12.892	0.483	0.071
				175.849	1298.019	0.167
				252.452	0.616	0.350
	3	0.826	44, 145, 246	33.123	11.272	0.480	0.117
				78.128	390.079	0.021
				187.900	186.987	0.149
				252.469	0.482	0.350
	4	0.896	55, 97, 163, 246	33.178	12.123	0.482	0.294
				75.522	119.910	0.017
				128.441	258.119	0.003
				185.922	82.920	0.142
				252.158	6.177	0.356
GA	1	2.410	244	69.838	4226.048	0.650	0.106	0.658
				252.452	0.616	0.350
	2	0.994	65, 242	33.239	13.806	0.483	0.147
				176.018	1256.142	0.166
				252.440	0.736	0.351
	3	0.857	45, 111, 242	33.131	11.350	0.481	0.195
				74.412	187.027	0.019
				186.725	207.543	0.150
				252.440	0.736	0.351
	4	0.882	44, 143, 155, 247	33.123	11.272	0.480	0.211
				77.924	377.966	0.021
				150.013	12.387	0.001
				188.193	191.885	0.149
				252.477	0.431	0.349
PSO	1	2.384	247	70.158	4274.185	0.651	0.083	0.584
				252.477	0.431	0.349
	2	0.955	65, 247	33.239	13.806	0.483	0.118
				176.672	1288.421	0.167
				252.477	0.431	0.349
	3	0.857	45, 111, 242	33.131	11.350	0.481	0.172
				74.412	187.027	0.019
				186.725	207.543	0.150
				252.440	0.736	0.351
	4	0.880	42, 135, 154, 247	33.097	11.070	0.479	0.211
				74.922	381.817	0.022
				144.535	35.001	0.001
				188.161	192.778	0.149
				252.477	0.431	0.349

The computational effort and parameters of each Gaussian distribution (${\theta }_j=\left\{w_j,{\mu }_j,{{\sigma }_j}^2\right\}$) are summarized in Table 4. Here, the number of iterations for the algorithms were 4, i.e., the proposed method optimized Equation (10) for d = [1, 2, 3, 4] before reaching the stopping criterion.

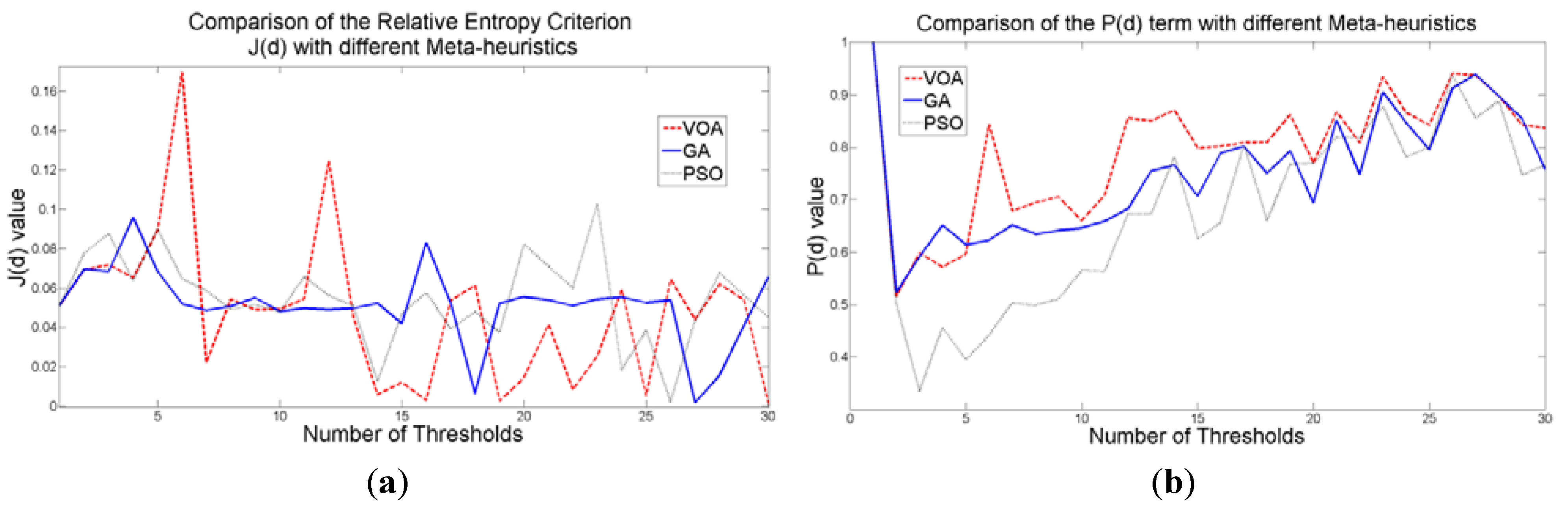
The behavior of the Relative Entropy function (Figure 7a) reveals its deficiency in detecting an appropriate number of distributions that will have a good description of the image histogram (Figure 8). The aforementioned is because as more distributions or thresholds are added into the mixture, it is impossible to identify a true minimum for the value of J(d) when implementing the three different meta-heuristic tools.

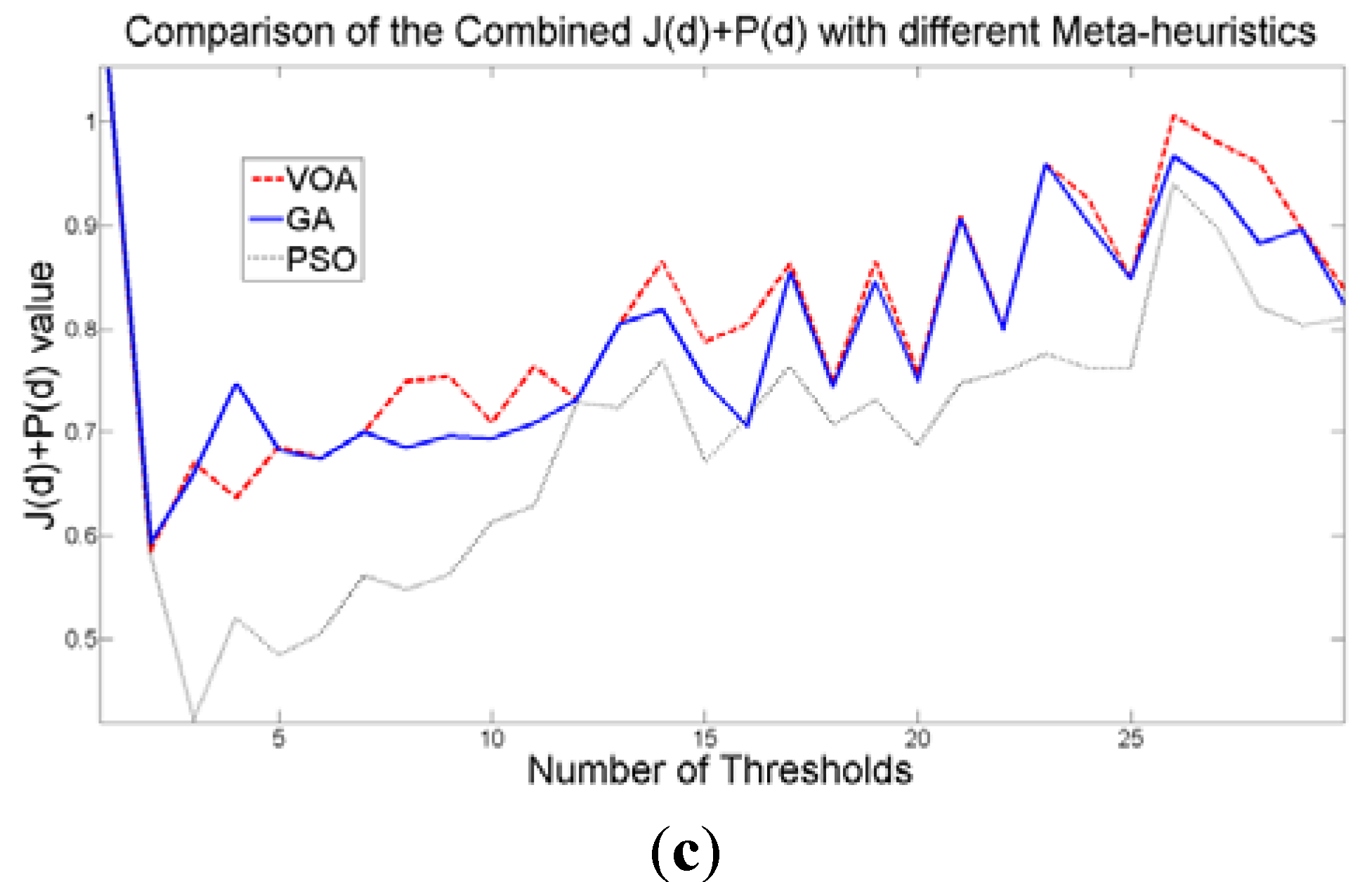
The additional function P(d) on the other hand shows a minimum value when a suitable number of distributions (which is the same as finding the number of thresholds) is found (Figure 7b), since its value shows an increasing pattern when more distributions are added to the mixture model. The combination of these two functions J(d) and P(d) shows that the optimal value for Θ(d) (Figure 7c) will be when the number of thresholds is three as P(d) suggested. Note that the purpose of J(d) is to find the best possible fitting with the suitable number of distributions (thresholds), and this is observed at Figure 8 where the fitted model (dotted line) provides a very good description of the original histogram (solid line) given by the image. The vertical dashed lines in Figure 8 are the values of the threshold found. In addition to the thresholding result, it was observed that VOA provides both, the smallest CPU time as well as the best objective function value among the three algorithms.

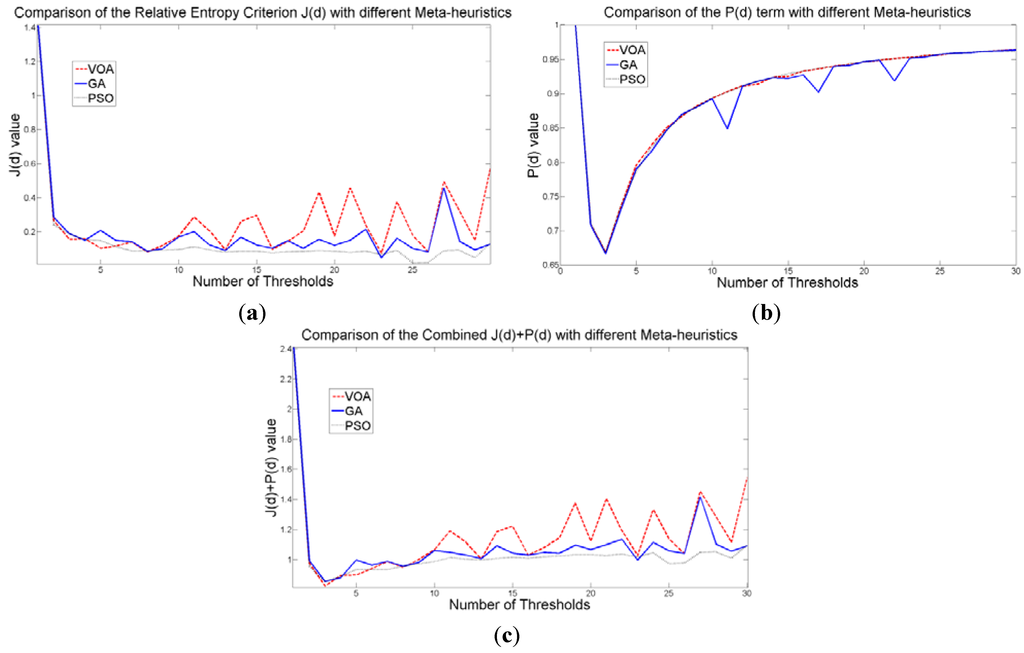
Figure 7. Behavior of (a) Relative Entropy function J(d), (b) P(d), and (c) Objective function Θ(d) over different numbers of thresholds with different meta-heuristics VOA, GA and PSO on test image 1.

Figure 7. Behavior of (a) Relative Entropy function J(d), (b) P(d), and (c) Objective function Θ(d) over different numbers of thresholds with different meta-heuristics VOA, GA and PSO on test image 1.

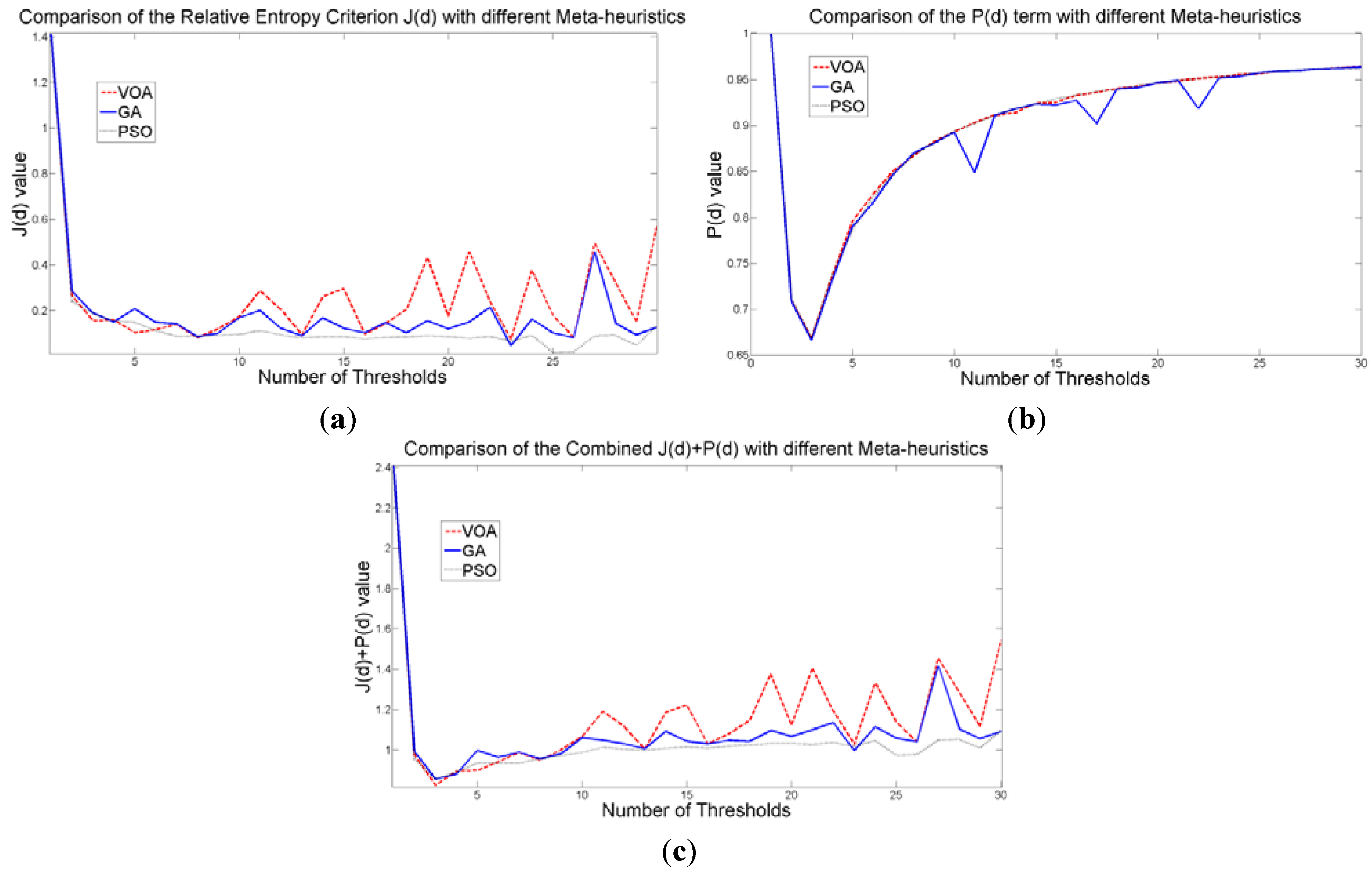
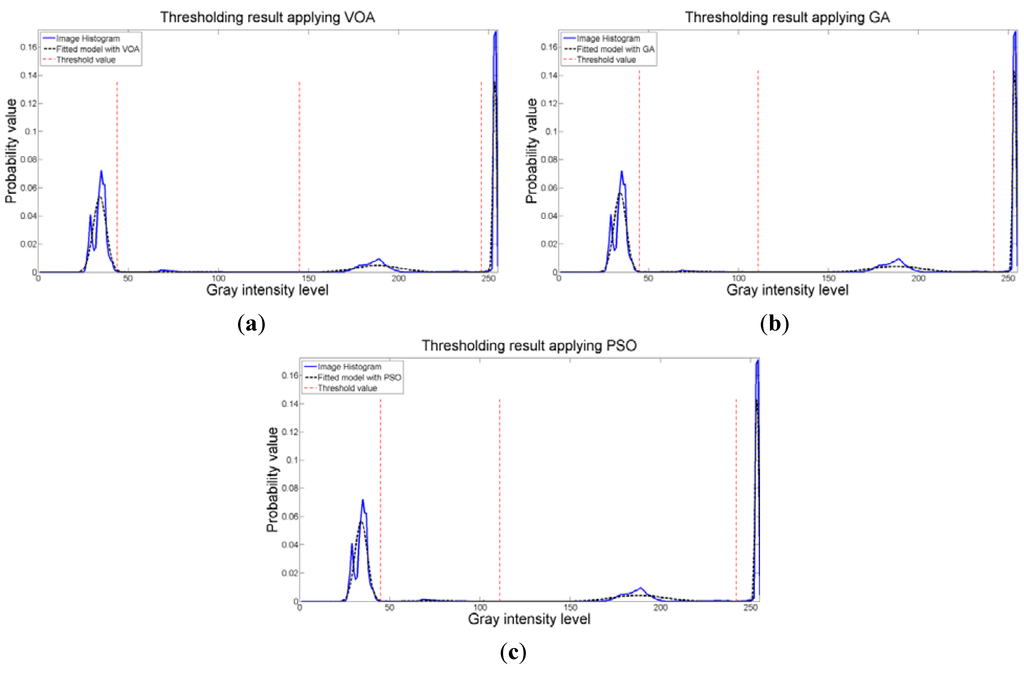
Figure 8. Fitting of the histogram of the test image 1 implementing (a) VOA, (b) GA, and (c) PSO.

Figure 8. Fitting of the histogram of the test image 1 implementing (a) VOA, (b) GA, and (c) PSO.

When implementing Otsu’s method, it is rather impressive to observe that the output image delivered by the algorithms when optimizing Equation (10) resembles the one given by Otsu’s method (Figure 4e). The aforementioned, confirms the competitiveness of the proposed idea in segmenting a gray scale image given a number of distributions in the mixture model. Additionally, the main contribution is that we do not need to look at the histogram to determine how many thresholds will provide a good segmentation, and by implementing optimization tools such as the ones presented in this study, we can provide satisfactory results in a short period of time, where methods such as Otsu’s would take too long.

Table 5. Thresholding results over 50 runs for the test image 2.

Algorithm	Number of Thresholds	Objective Function	Threshold Values	Means	Variances	Weights	CPU Time per Iteration (s)	Total CPU Time for the Proposed Approach (s)
VOA	1	1.051	143	87.326	1015.901	0.127	0.057	0.237
				203.855	603.462	0.873
	2	0.585	133, 205	81.590	808.054	0.114	0.089
				182.352	280.586	0.448
				223.915	170.129	0.438
	3	0.670	104, 174, 209	67.393	370.007	0.082	0.091
				150.866	385.486	0.153
				192.994	90.775	0.378
				226.231	146.602	0.386
GA	1	1.051	142	86.658	991.336	0.126	0.109	0.480
				203.746	609.117	0.874
	2	0.593	132, 204	81.075	790.076	0.113	0.145
				181.537	279.992	0.436
				223.310	176.642	0.451
	3	0.659	142, 149, 206	86.658	991.336	0.126	0.226
				145.121	3.989	0.011
				185.213	205.948	0.440
				224.558	163.332	0.423
PSO	1	1.051	143	87.326	1015.901	0.127	0.072	0.453
				203.855	603.462	0.873
	2	0.573	156, 206	97.751	1389.414	0.153	0.141
				186.458	170.789	0.424
				224.558	163.332	0.423
	3	0.619	101, 180, 211	66.048	335.944	0.079	0.240
				155.144	453.146	0.195
				195.932	76.337	0.366
				227.489	134.942	0.359

Table 5. Thresholding results over 50 runs for the test image 2.

Algorithm	Number of Thresholds	Objective Function	Threshold Values	Means	Variances	Weights	CPU Time per Iteration (s)	Total CPU Time for the Proposed Approach (s)
VOA	1	1.051	143	87.326	1015.901	0.127	0.057	0.237
				203.855	603.462	0.873
	2	0.585	133, 205	81.590	808.054	0.114	0.089
				182.352	280.586	0.448
				223.915	170.129	0.438
	3	0.670	104, 174, 209	67.393	370.007	0.082	0.091
				150.866	385.486	0.153
				192.994	90.775	0.378
				226.231	146.602	0.386
GA	1	1.051	142	86.658	991.336	0.126	0.109	0.480
				203.746	609.117	0.874
	2	0.593	132, 204	81.075	790.076	0.113	0.145
				181.537	279.992	0.436
				223.310	176.642	0.451
	3	0.659	142, 149, 206	86.658	991.336	0.126	0.226
				145.121	3.989	0.011
				185.213	205.948	0.440
				224.558	163.332	0.423
PSO	1	1.051	143	87.326	1015.901	0.127	0.072	0.453
				203.855	603.462	0.873
	2	0.573	156, 206	97.751	1389.414	0.153	0.141
				186.458	170.789	0.424
				224.558	163.332	0.423
	3	0.619	101, 180, 211	66.048	335.944	0.079	0.240
				155.144	453.146	0.195
				195.932	76.337	0.366
				227.489	134.942	0.359

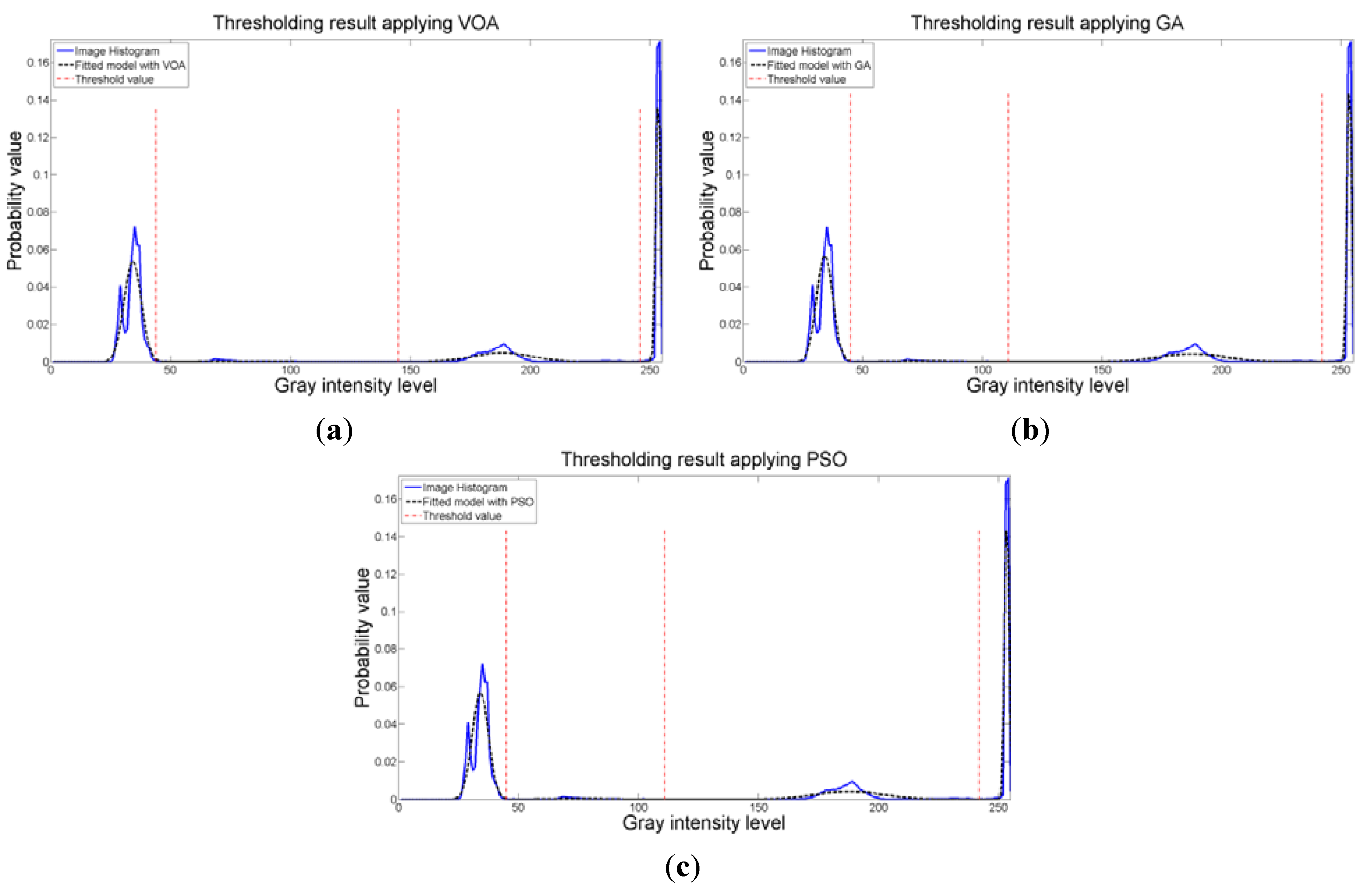
When an image containing text on a wrinkled paper (Figure 5a) is tested, two thresholds (or three Gaussian distributions) give the best objective function value for Equation (10) as observed in Figure 9c. Table 5 summarizes the thresholding results, i.e., Θ(d), computational effort and Gaussian parameters, for the three meta-heuristics implemented. As for the fitting result, Figure 10 shows that even though three Gaussian distributions do not provide an exact description of the image histogram, it is good enough to recognize all the characters on the thresholded image (Figure 5b–d).

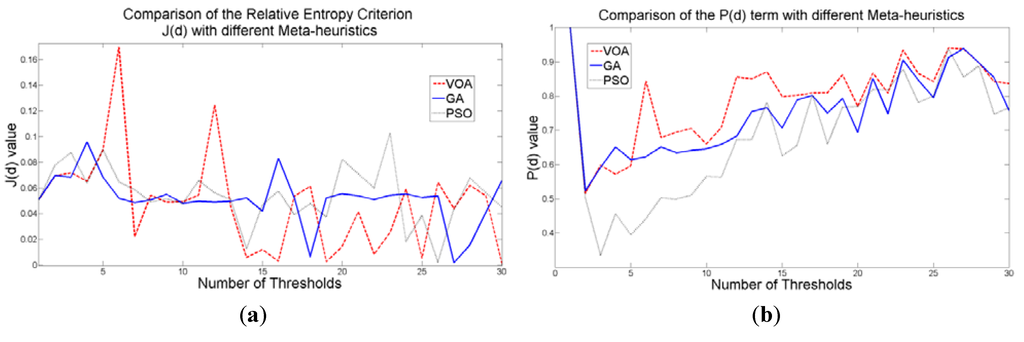
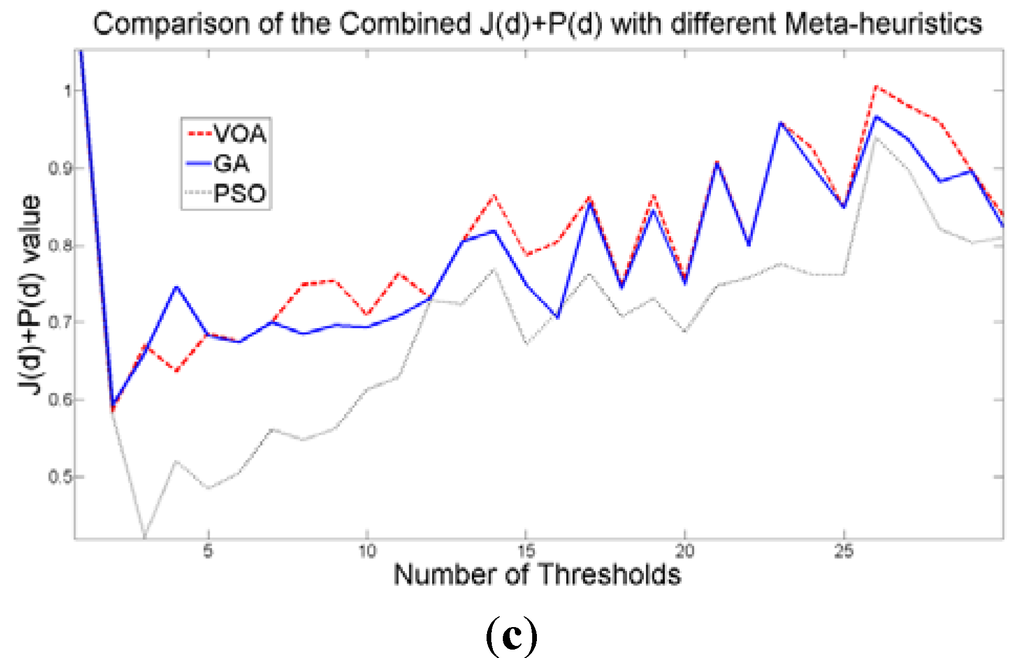
Figure 9. Behavior of (a) Relative Entropy function J(d), (b) P(d), and (c) Objective function Θ(d) over different numbers of thresholds with different meta-heuristics VOA, GA and PSO on test image 2.

Figure 9. Behavior of (a) Relative Entropy function J(d), (b) P(d), and (c) Objective function Θ(d) over different numbers of thresholds with different meta-heuristics VOA, GA and PSO on test image 2.

The outstanding performance of the three meta-heuristics is observed once again when comparing with the Otsu’s method (Figure 5e), where the computational effort shows the feasibility of optimizing the proposed mathematical model with heuristic optimization algorithms.

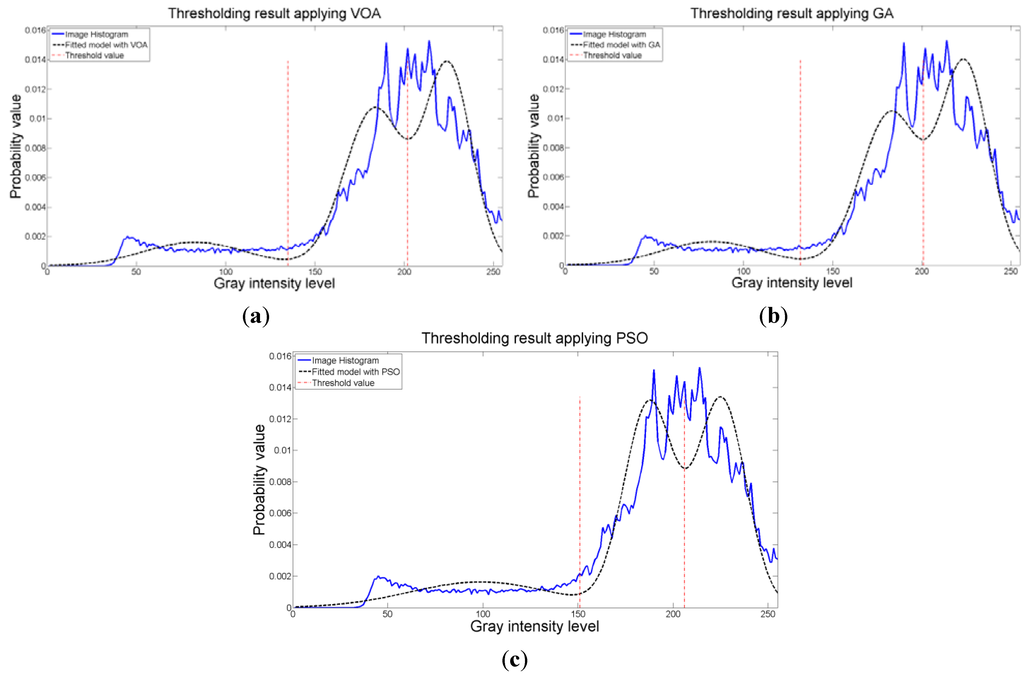
Figure 10. Fitting of the histogram of the test image 2 implementing (a) VOA, (b) GA, and (c) PSO.

Figure 10. Fitting of the histogram of the test image 2 implementing (a) VOA, (b) GA, and (c) PSO.

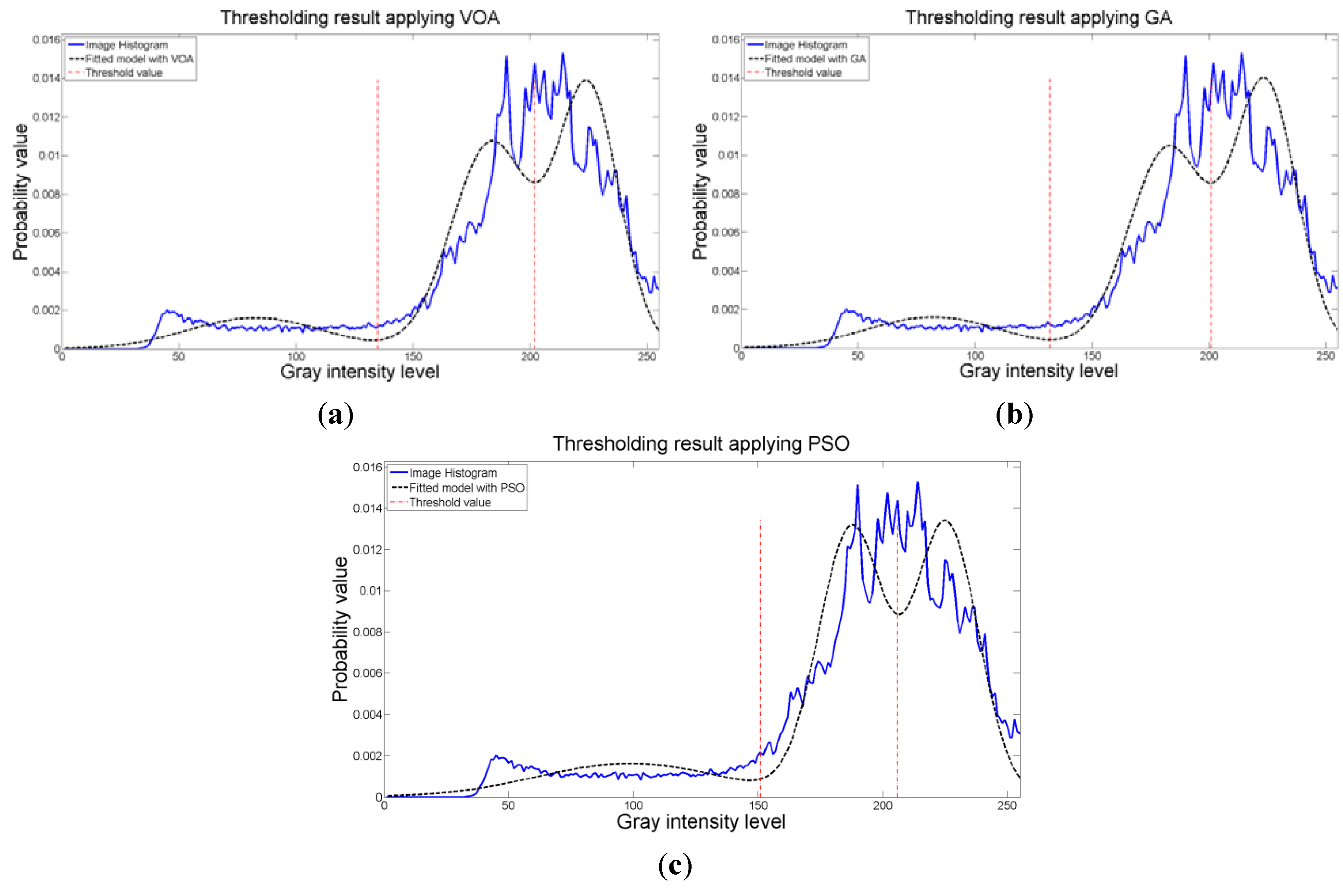
The thresholding results of the Lena image (Figure 6a) shows that four thresholds (five Gaussian distributions) have the best objective function value, which is detailed in Table 6. Visually, the thresholded images (Figure 6b–d) obtain most of the details from the original one, and in terms of objective function behavior (Figure 11) there is no need to add more distributions into the mixture model (i.e., more thresholds) because they do not provide a better objective function value.

Table 6. Thresholding results over 50 runs for the test image 3.

Algorithm	Number of Thresholds	Objective Function	Threshold Values	Means	Variances	Weights	CPU Time per Iteration (s)	Total CPU Time for the Proposed Approach (s)
VOA	1	1.043	63	48.917	51.398	0.159	0.046	1.009
				138.048	1442.095	0.841
	2	0.575	59, 138	47.598	40.100	0.143	0.128
				104.785	484.361	0.430
				168.523	538.213	0.428
	3	0.454	99, 140, 183	65.002	369.233	0.302	0.198
				120.137	147.621	0.287
				157.234	130.155	0.295
				201.595	109.646	0.116
	4	0.367	86, 126, 154, 199	57.243	192.433	0.236	0.210
				106.550	126.938	0.236
				139.629	67.666	0.241
				170.694	173.733	0.218
				208.851	42.459	0.068
	5	0.466	68, 104, 134, 156, 190	50.380	68.188	0.175	0.428
				88.813	108.622	0.165
				120.054	77.656	0.203
				145.072	39.845	0.192
				168.597	90.400	0.167
				204.364	77.722	0.098
GA	1	1.044	66	49.794	60.874	0.169	0.103	0.904
				138.924	1393.456	0.831
	2	0.606	69, 139	50.671	72.095	0.178	0.136
				109.090	368.075	0.402
				169.106	530.358	0.419
	3	0.504	96, 140, 179	62.664	315.826	0.282	0.182
				118.590	171.180	0.307
				156.168	110.243	0.282
				199.453	139.510	0.129
	4	0.474	46, 99, 136, 169	40.698	14.583	0.051	0.225
				69.954	296.623	0.251
				118.032	124.129	0.256
				151.053	77.603	0.267
				192.624	235.736	0.175
	5	0.584	65, 87, 128, 152, 205	49.504	57.550	0.166	0.258
				76.023	40.415	0.074
				108.258	138.292	0.250
				139.533	49.522	0.205
				171.707	244.613	0.257
				211.824	28.018	0.049
PSO	1	1.044	64	49.212	54.387	0.163	0.096	0.887
				138.353	1424.978	0.837
	2	0.575	68, 140	50.380	68.188	0.175	0.128
				109.403	387.984	0.414
				169.718	522.330	0.411
	3	0.446	97, 141, 191	63.440	333.741	0.288	0.170
				119.639	170.199	0.309
				159.625	168.784	0.308
				204.790	73.728	0.095
	4	0.337	79, 121, 148, 184	54.216	131.179	0.210	0.220
				101.036	126.541	0.225
				134.327	60.474	0.225
				161.866	95.355	0.227
				202.037	103.844	0.113
	5	0.478	60, 115, 117, 147, 186	47.926	42.582	0.147	0.273
				90.827	237.679	0.255
				115.514	0.250	0.010
				132.322	71.331	0.240
				161.755	107.986	0.240
				202.782	94.639	0.108

Table 6. Thresholding results over 50 runs for the test image 3.

Algorithm	Number of Thresholds	Objective Function	Threshold Values	Means	Variances	Weights	CPU Time per Iteration (s)	Total CPU Time for the Proposed Approach (s)
VOA	1	1.043	63	48.917	51.398	0.159	0.046	1.009
				138.048	1442.095	0.841
	2	0.575	59, 138	47.598	40.100	0.143	0.128
				104.785	484.361	0.430
				168.523	538.213	0.428
	3	0.454	99, 140, 183	65.002	369.233	0.302	0.198
				120.137	147.621	0.287
				157.234	130.155	0.295
				201.595	109.646	0.116
	4	0.367	86, 126, 154, 199	57.243	192.433	0.236	0.210
				106.550	126.938	0.236
				139.629	67.666	0.241
				170.694	173.733	0.218
				208.851	42.459	0.068
	5	0.466	68, 104, 134, 156, 190	50.380	68.188	0.175	0.428
				88.813	108.622	0.165
				120.054	77.656	0.203
				145.072	39.845	0.192
				168.597	90.400	0.167
				204.364	77.722	0.098
GA	1	1.044	66	49.794	60.874	0.169	0.103	0.904
				138.924	1393.456	0.831
	2	0.606	69, 139	50.671	72.095	0.178	0.136
				109.090	368.075	0.402
				169.106	530.358	0.419
	3	0.504	96, 140, 179	62.664	315.826	0.282	0.182
				118.590	171.180	0.307
				156.168	110.243	0.282
				199.453	139.510	0.129
	4	0.474	46, 99, 136, 169	40.698	14.583	0.051	0.225
				69.954	296.623	0.251
				118.032	124.129	0.256
				151.053	77.603	0.267
				192.624	235.736	0.175
	5	0.584	65, 87, 128, 152, 205	49.504	57.550	0.166	0.258
				76.023	40.415	0.074
				108.258	138.292	0.250
				139.533	49.522	0.205
				171.707	244.613	0.257
				211.824	28.018	0.049
PSO	1	1.044	64	49.212	54.387	0.163	0.096	0.887
				138.353	1424.978	0.837
	2	0.575	68, 140	50.380	68.188	0.175	0.128
				109.403	387.984	0.414
				169.718	522.330	0.411
	3	0.446	97, 141, 191	63.440	333.741	0.288	0.170
				119.639	170.199	0.309
				159.625	168.784	0.308
				204.790	73.728	0.095
	4	0.337	79, 121, 148, 184	54.216	131.179	0.210	0.220
				101.036	126.541	0.225
				134.327	60.474	0.225
				161.866	95.355	0.227
				202.037	103.844	0.113
	5	0.478	60, 115, 117, 147, 186	47.926	42.582	0.147	0.273
				90.827	237.679	0.255
				115.514	0.250	0.010
				132.322	71.331	0.240
				161.755	107.986	0.240
				202.782	94.639	0.108

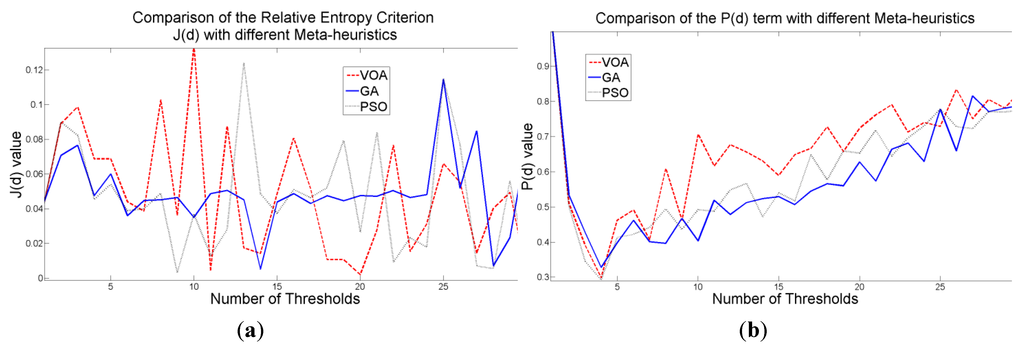
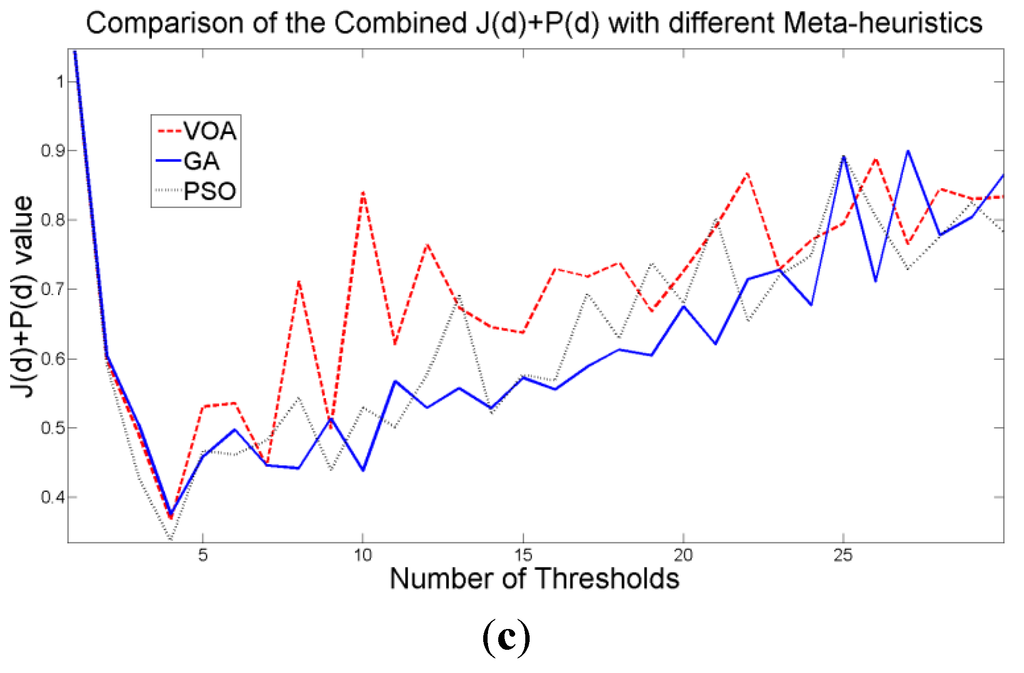
Figure 11. Behavior of (a) Relative Entropy function J(d), (b) P(d), and (c) Objective function Θ(d) over different numbers of thresholds with different meta-heuristics VOA, GA and PSO on test image 3.

Figure 11. Behavior of (a) Relative Entropy function J(d), (b) P(d), and (c) Objective function Θ(d) over different numbers of thresholds with different meta-heuristics VOA, GA and PSO on test image 3.

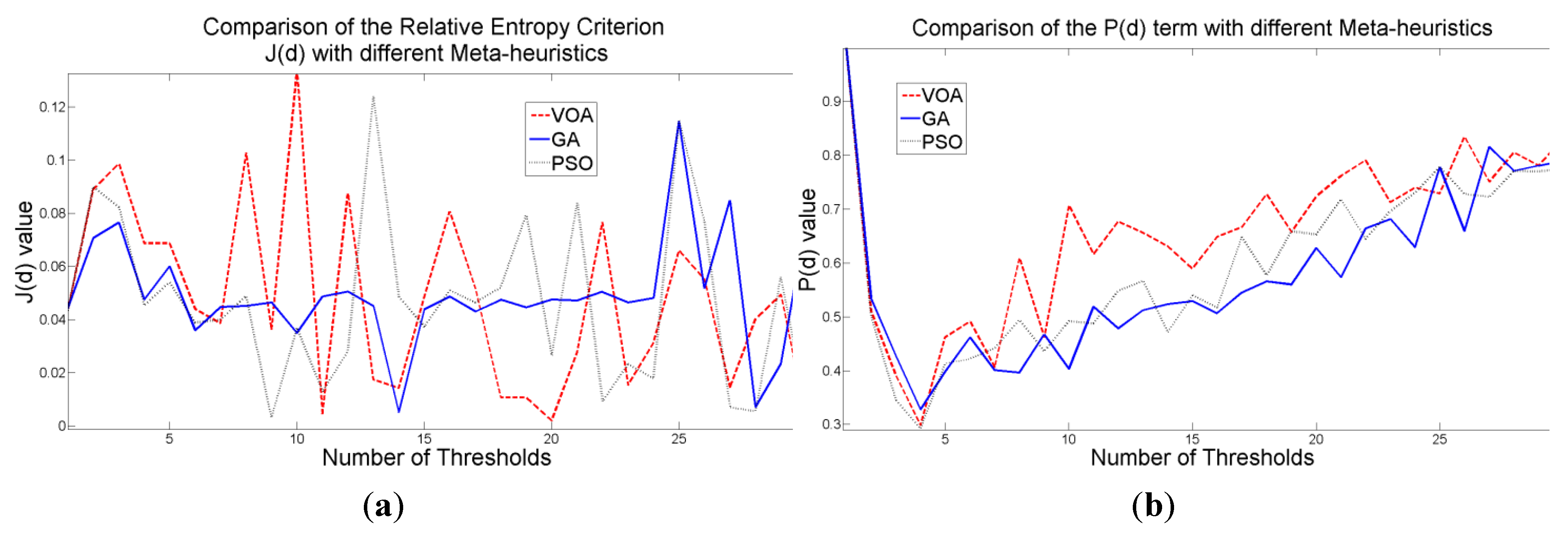
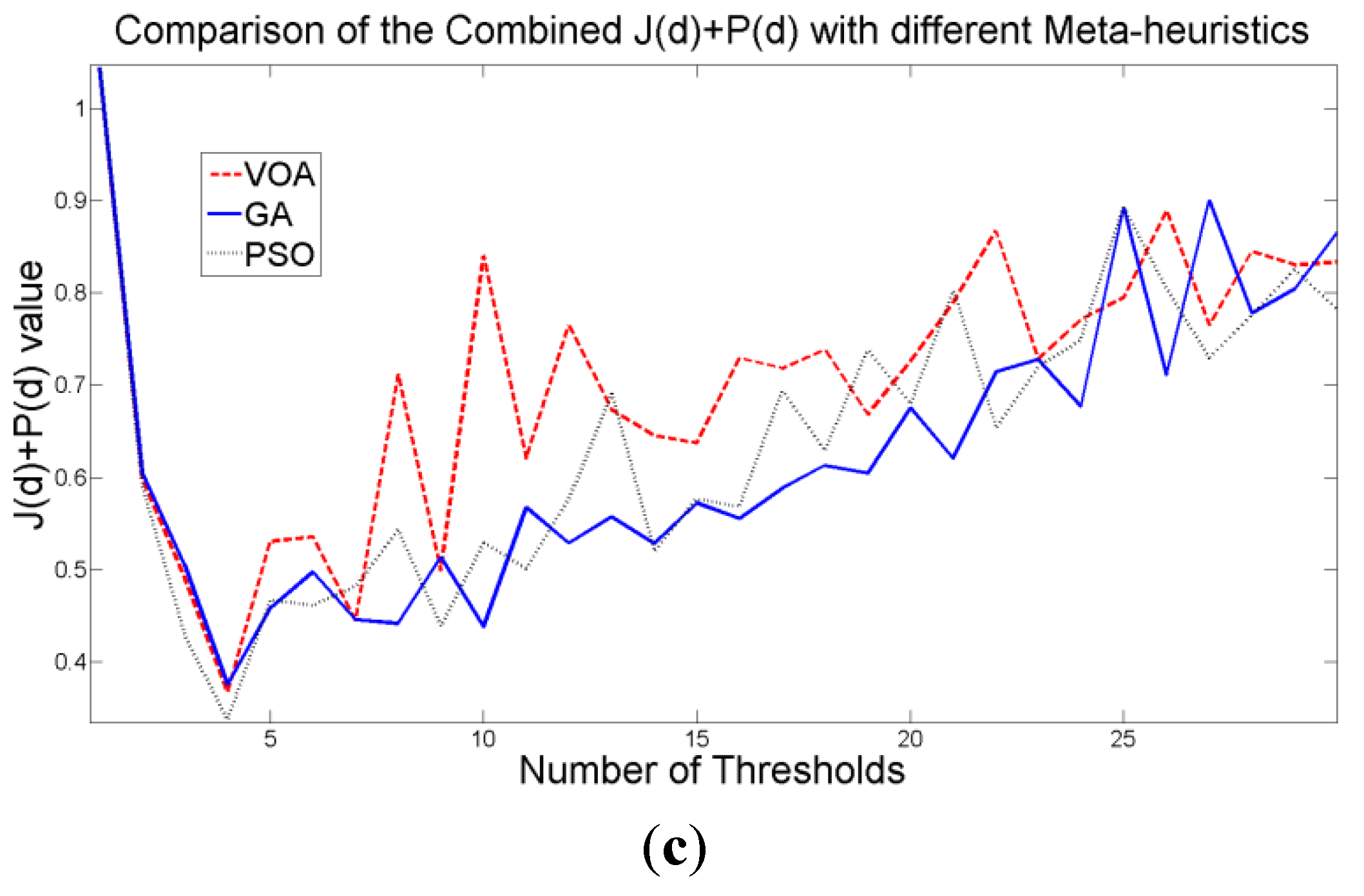
Once again, the fitting provided by the mixture model (Figure 12) might not be the best; however, it is good enough to provide most of the details from the original image. It is interesting to observe that all the algorithmic tools are able to find satisfactory results in no more than 1.009 seconds in the case of VOA which is the slowest one, even though the algorithmic tools had to optimize Equation (10) for d = [1, 2, 3, 4].

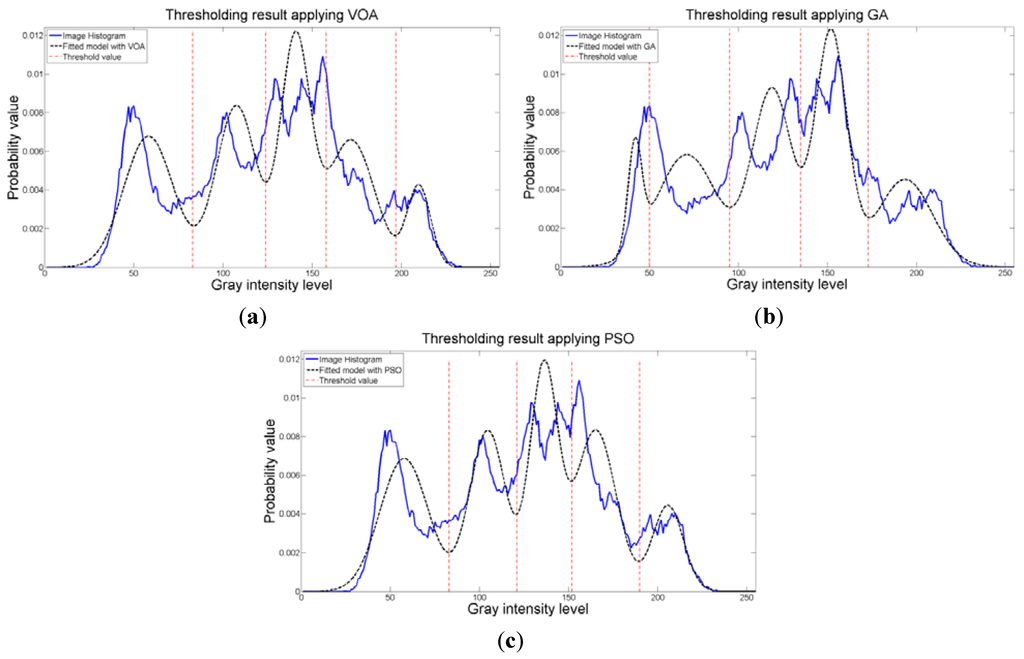
Figure 12. Fitting of the histogram of the test image 3 implementing (a) VOA, (b) GA, and (c) PSO.

Figure 12. Fitting of the histogram of the test image 3 implementing (a) VOA, (b) GA, and (c) PSO.

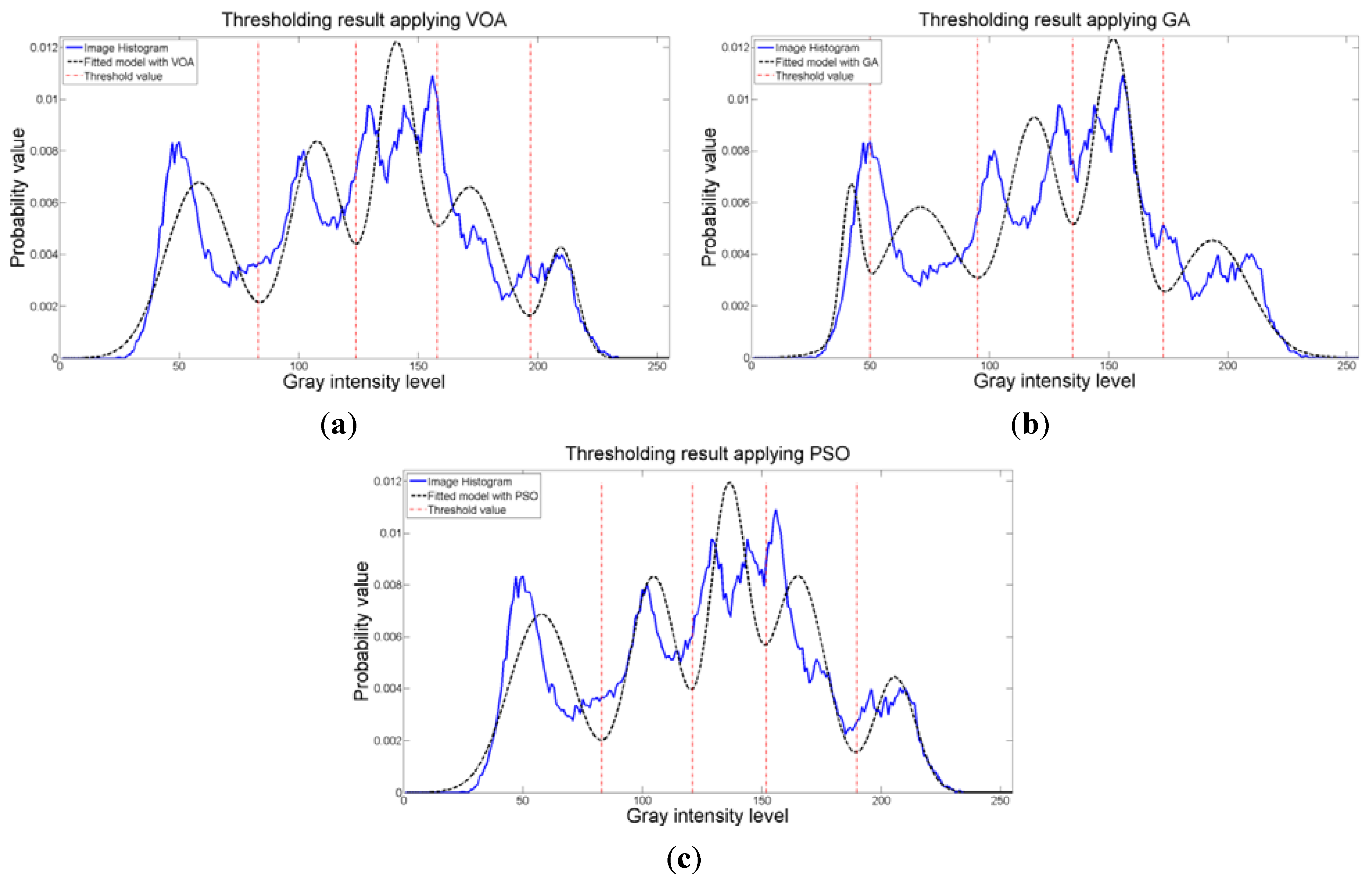
To further test the proposed method an image with low contrast is used as illustrated in Figure 13a. It is observed that all the algorithmic tools are able to segment the image providing the correct number of thresholds which is three. Additionally, when comparing the output image given by Otsu’s method and the idea proposed in this study, we are able to observe that despite its novelty the proposed method provides stable and satisfactory results for a low contrast image.

Three thresholds are suggested after the optimization of Equation (10) is performed, which is good enough for successfully segmenting the image under study (Figure 13b–d), though the fitting of the image histogram was not a perfect one (Figure 15). More importantly, the addition of more than four distributions (i.e., three thresholds) to the mathematical model Equation (10) does not achieve a better result according to Figure 14c; therefore, the power of the proposed approach is shown once again with this instance. As for the Otsu’s method, even though the correct number of thresholds is provided, the low contrast causes defect in the output image (seen at the light gray region in the middle of Figure 13e.

Table 7. Thresholding result over 50 runs for the test image 4.

Algorithm	Number of Thresholds	Objective Function	Threshold Values	Means	Variances	Weights	CPU Time per Iteration (s)	Total CPU Time for the Proposed Approach (s)
VOA	1	2.112	98	102.027	504.595	0.612	0.045	0.213
				174.622	36.165	0.388
	2	1.014	105, 169	91.007	2.994	0.486	0.051
				146.853	157.462	0.160
				176.415	0.749	0.354
	3	0.848	101, 133, 169	90.917	1.888	0.482	0.054
				109.438	46.637	0.019
				150.667	17.258	0.145
				176.415	0.749	0.354
	4	0.919	103, 117, 140, 169	90.929	2.009	0.483	0.064
				107.796	17.853	0.016
				126.818	25.714	0.002
				150.202	9.141	0.139
				176.271	2.326	0.359
GA	1	2.112	98	90.906	1.803	0.482	0.134	0.692
				166.703	268.234	0.518
	2	1.051	100, 166	90.914	1.861	0.482	0.153
				145.534	191.624	0.161
				176.349	1.354	0.357
	3	0.903	99, 122, 167	90.910	1.832	0.482	0.179
				107.759	23.640	0.018
				150.171	19.452	0.144
				176.364	1.203	0.356
	4	0.998	109, 115, 139, 177	91.270	6.829	0.494	0.225
				111.849	2.575	0.003
				123.655	52.305	0.005
				164.654	163.335	0.323
				177.000	1.455	0.176
PSO	1	2.112	98	90.906	1.803	0.482	0.027	0.171
				166.703	268.234	0.518
	2	1.005	97, 168	90.902	1.780	0.481	0.035
				145.505	204.582	0.163
				176.393	0.931	0.355
	3	0.873	98, 116, 168	90.906	1.803	0.482	0.045
				106.393	12.956	0.016
				149.899	33.945	0.147
				176.393	0.931	0.355
	4	0.911	98, 130, 138, 169	90.906	1.803	0.482	0.065
				108.777	42.833	0.019
				133.110	4.122	0.001
				150.704	16.707	0.144
				176.415	0.749	0.354

Table 7. Thresholding result over 50 runs for the test image 4.

Algorithm	Number of Thresholds	Objective Function	Threshold Values	Means	Variances	Weights	CPU Time per Iteration (s)	Total CPU Time for the Proposed Approach (s)
VOA	1	2.112	98	102.027	504.595	0.612	0.045	0.213
				174.622	36.165	0.388
	2	1.014	105, 169	91.007	2.994	0.486	0.051
				146.853	157.462	0.160
				176.415	0.749	0.354
	3	0.848	101, 133, 169	90.917	1.888	0.482	0.054
				109.438	46.637	0.019
				150.667	17.258	0.145
				176.415	0.749	0.354
	4	0.919	103, 117, 140, 169	90.929	2.009	0.483	0.064
				107.796	17.853	0.016
				126.818	25.714	0.002
				150.202	9.141	0.139
				176.271	2.326	0.359
GA	1	2.112	98	90.906	1.803	0.482	0.134	0.692
				166.703	268.234	0.518
	2	1.051	100, 166	90.914	1.861	0.482	0.153
				145.534	191.624	0.161
				176.349	1.354	0.357
	3	0.903	99, 122, 167	90.910	1.832	0.482	0.179
				107.759	23.640	0.018
				150.171	19.452	0.144
				176.364	1.203	0.356
	4	0.998	109, 115, 139, 177	91.270	6.829	0.494	0.225
				111.849	2.575	0.003
				123.655	52.305	0.005
				164.654	163.335	0.323
				177.000	1.455	0.176
PSO	1	2.112	98	90.906	1.803	0.482	0.027	0.171
				166.703	268.234	0.518
	2	1.005	97, 168	90.902	1.780	0.481	0.035
				145.505	204.582	0.163
				176.393	0.931	0.355
	3	0.873	98, 116, 168	90.906	1.803	0.482	0.045
				106.393	12.956	0.016
				149.899	33.945	0.147
				176.393	0.931	0.355
	4	0.911	98, 130, 138, 169	90.906	1.803	0.482	0.065
				108.777	42.833	0.019
				133.110	4.122	0.001
				150.704	16.707	0.144
				176.415	0.749	0.354

Figure 13. Test image 4: (a) Original image; Thresholded image implementing (b) VOA, (c) GA, (d) PSO, and (e) Otsu’s method.

Figure 13. Test image 4: (a) Original image; Thresholded image implementing (b) VOA, (c) GA, (d) PSO, and (e) Otsu’s method.

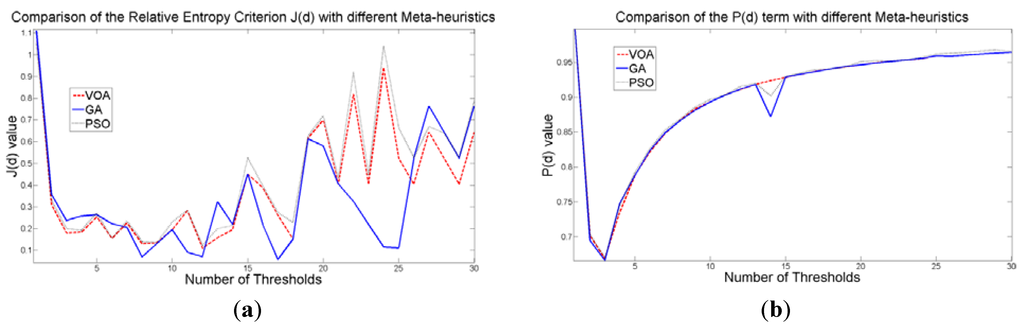
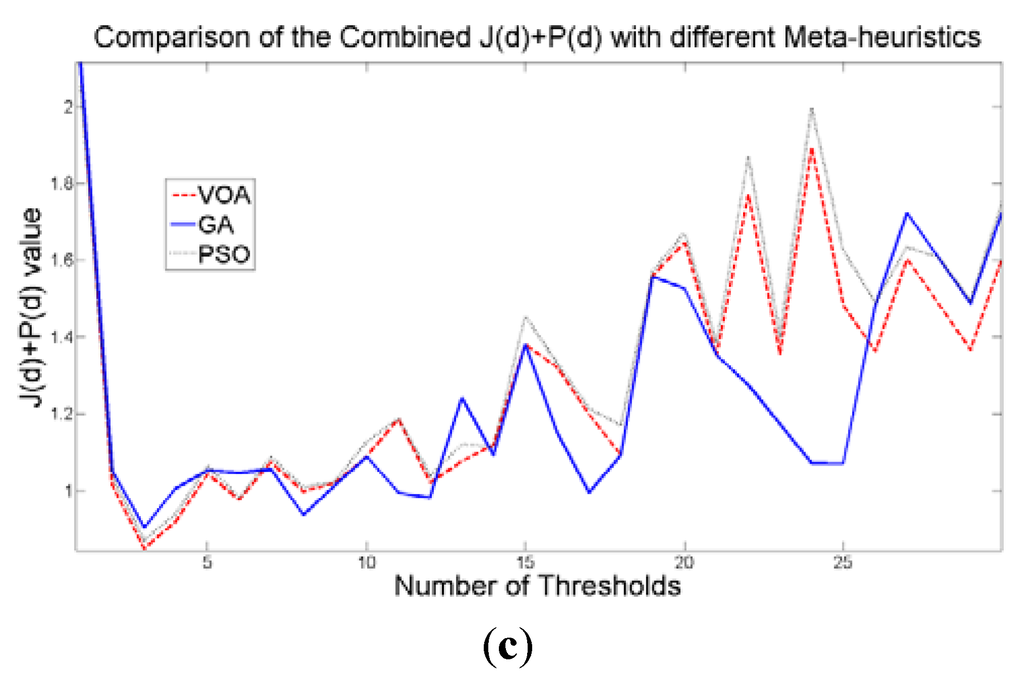
Figure 14. Behavior of (a) Relative Entropy function J(d), (b) P(d), and (c) Objective function Θ(d) over different numbers of thresholds with different meta-heuristics VOA, GA, and PSO on test image 4.

Figure 14. Behavior of (a) Relative Entropy function J(d), (b) P(d), and (c) Objective function Θ(d) over different numbers of thresholds with different meta-heuristics VOA, GA, and PSO on test image 4.

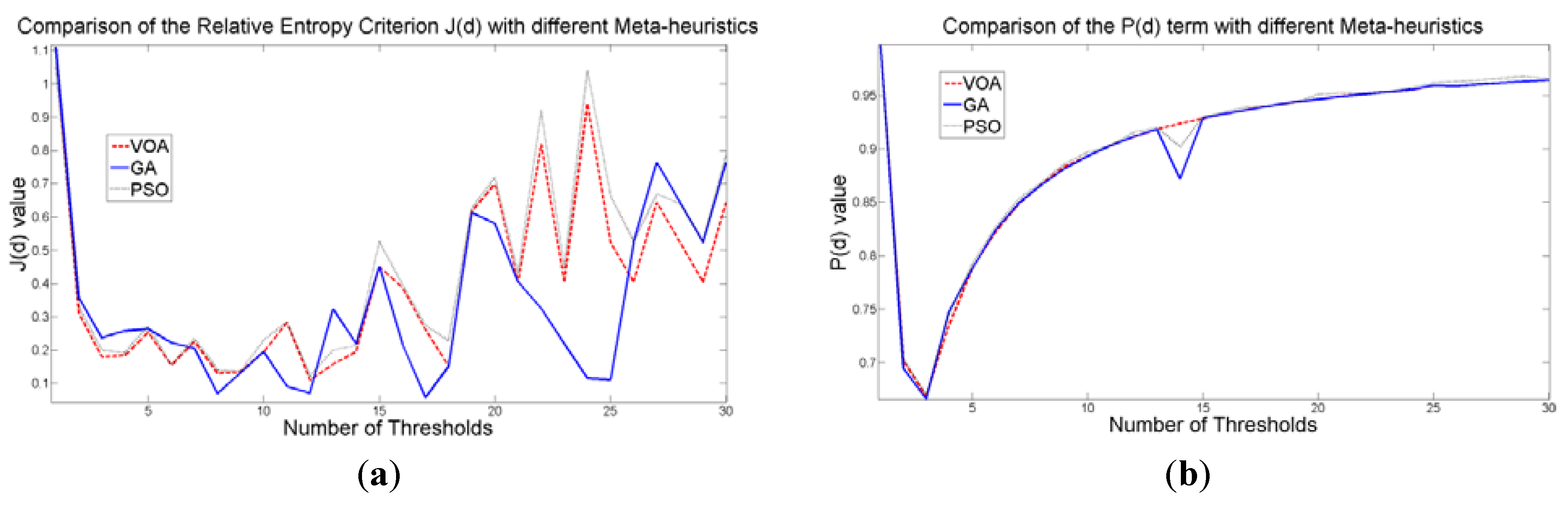
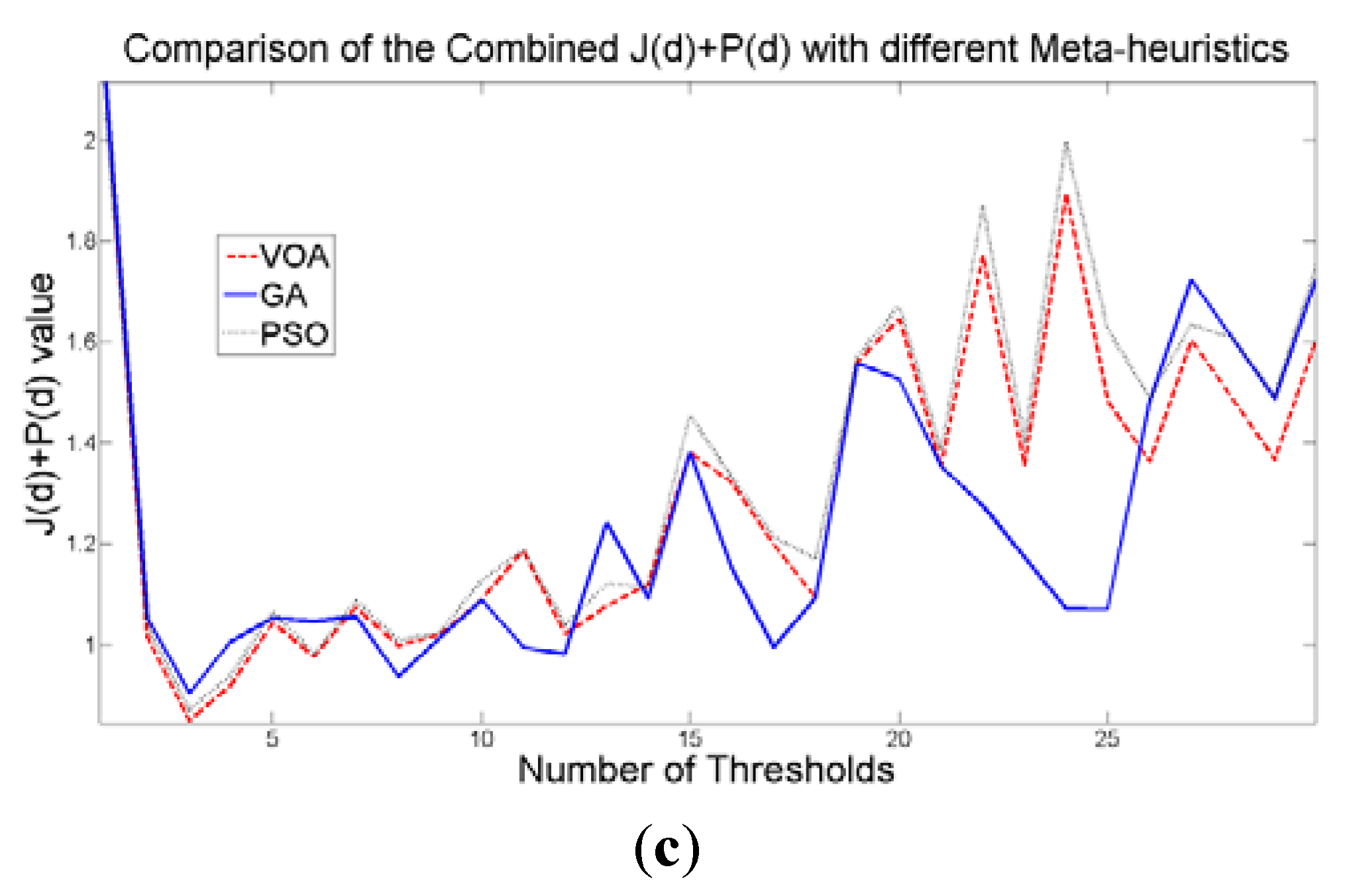
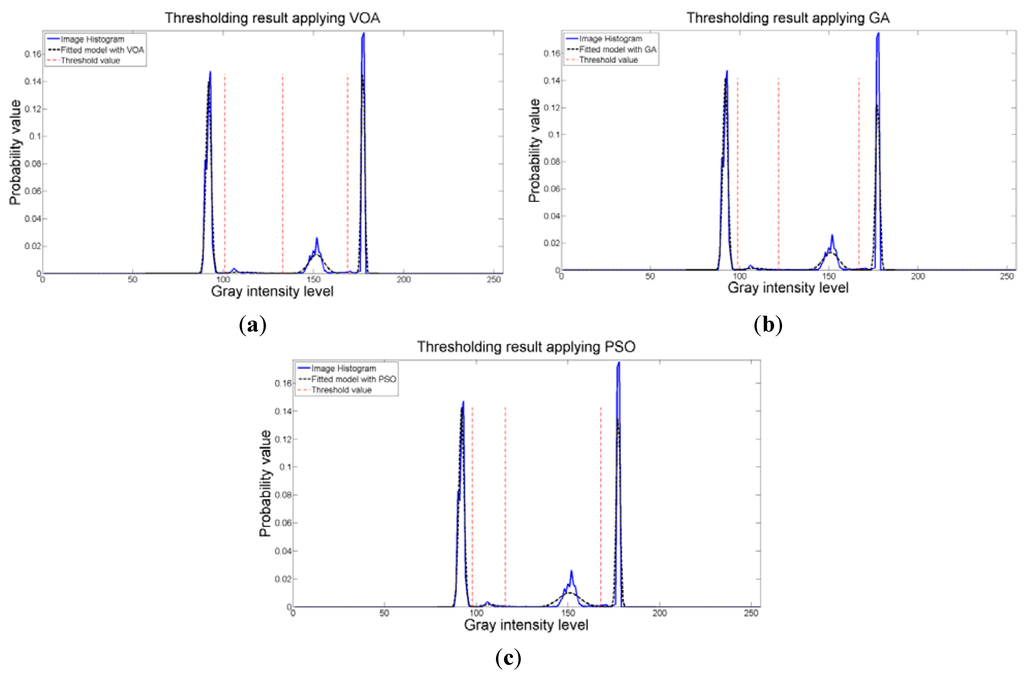
Figure 15. Fitting of the histogram of the test image 4 implementing (a) VOA, (b) GA, and (c) PSO.

Figure 15. Fitting of the histogram of the test image 4 implementing (a) VOA, (b) GA, and (c) PSO.

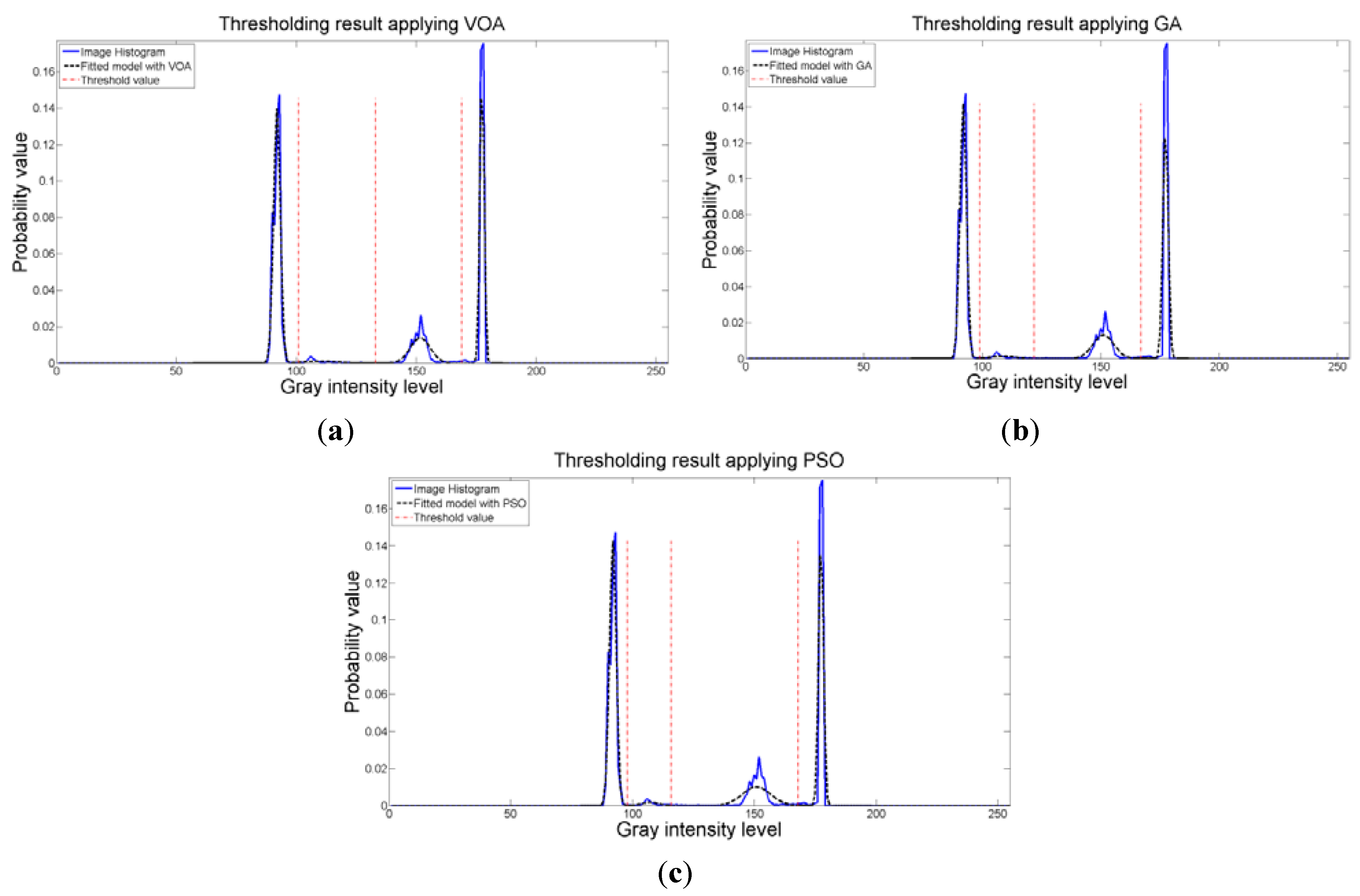
Table 8. Thresholding result over 50 runs for the test image 5.

Algorithm	Number of Thresholds	Objective Function	Threshold Values	Means	Variances	Weights	CPU Time per Iteration (s)	Total CPU Time for the Proposed Approach (s)
VOA	1	1.023	67	48.328	119.083	0.172	0.060	0.435
				138.301	1428.555	0.828
	2	0.556	63, 137	46.555	100.292	0.155	0.075
				104.962	436.410	0.421
				168.426	564.154	0.424
	3	0.504	88, 140, 206	57.730	278.208	0.254	0.082
				115.780	221.287	0.346
				165.005	334.790	0.358
				214.735	50.956	0.042
	4	0.481	87, 130, 151, 197	57.218	267.832	0.249	0.094
				109.591	151.059	0.268
				140.153	36.619	0.178
				168.811	169.302	0.232
				209.138	78.820	0.071
	5	0.495	77, 116, 143, 158, 214, 255	52.347	176.710	0.208	0.124
				97.798	120.079	0.210
				129.636	59.464	0.208
				149.842	18.471	0.128
				180.649	270.308	0.226
				220.581	34.873	0.020
GA	1	1.024	71	49.927	139.317	0.187	0.139	1.204
				139.577	1363.879	0.813
	2	0.669	76, 137	51.913	169.499	0.204	0.198
				109.784	294.414	0.372
				168.426	564.154	0.424
	3	0.586	84, 138, 227	55.674	237.243	0.236	0.209
				113.180	235.410	0.347
				168.529	529.908	0.413
				231.261	20.782	0.003
	4	0.568	60, 103, 146, 211	45.138	87.633	0.141	0.259
				82.720	165.607	0.195
				125.553	152.188	0.316
				170.644	343.107	0.320
				218.253	40.308	0.028
	5	0.573	57, 90, 130, 156, 212	43.635	76.301	0.126	0.400
				72.881	99.772	0.138
				110.800	131.973	0.254
				142.590	55.391	0.220
				178.408	270.837	0.237
				219.035	38.368	0.025
PSO	1	1.023	66	47.900	114.220	0.168	0.034	0.373
				137.948	1446.983	0.832
	2	0.564	64, 137	47.023	104.922	0.159	0.060
				105.419	421.751	0.416
				168.426	564.154	0.424
	3	0.413	97, 140, 182	63.047	390.706	0.300	0.073
				119.448	154.217	0.300
				157.206	130.606	0.281
				201.012	152.773	0.119
	4	0.410	28, 89, 133, 169	22.825	17.056	0.007	0.091
				59.246	263.407	0.252
				112.179	160.043	0.284
				149.441	99.432	0.282
				192.596	259.838	0.175
	5	0.576	40, 70, 125, 159, 230	32.580	32.714	0.037	0.115
				53.830	68.546	0.146
				100.401	235.202	0.297
				141.671	92.691	0.281
				184.398	346.042	0.237
				234.122	19.797	0.002

Table 8. Thresholding result over 50 runs for the test image 5.

Algorithm	Number of Thresholds	Objective Function	Threshold Values	Means	Variances	Weights	CPU Time per Iteration (s)	Total CPU Time for the Proposed Approach (s)
VOA	1	1.023	67	48.328	119.083	0.172	0.060	0.435
				138.301	1428.555	0.828
	2	0.556	63, 137	46.555	100.292	0.155	0.075
				104.962	436.410	0.421
				168.426	564.154	0.424
	3	0.504	88, 140, 206	57.730	278.208	0.254	0.082
				115.780	221.287	0.346
				165.005	334.790	0.358
				214.735	50.956	0.042
	4	0.481	87, 130, 151, 197	57.218	267.832	0.249	0.094
				109.591	151.059	0.268
				140.153	36.619	0.178
				168.811	169.302	0.232
				209.138	78.820	0.071
	5	0.495	77, 116, 143, 158, 214, 255	52.347	176.710	0.208	0.124
				97.798	120.079	0.210
				129.636	59.464	0.208
				149.842	18.471	0.128
				180.649	270.308	0.226
				220.581	34.873	0.020
GA	1	1.024	71	49.927	139.317	0.187	0.139	1.204
				139.577	1363.879	0.813
	2	0.669	76, 137	51.913	169.499	0.204	0.198
				109.784	294.414	0.372
				168.426	564.154	0.424
	3	0.586	84, 138, 227	55.674	237.243	0.236	0.209
				113.180	235.410	0.347
				168.529	529.908	0.413
				231.261	20.782	0.003
	4	0.568	60, 103, 146, 211	45.138	87.633	0.141	0.259
				82.720	165.607	0.195
				125.553	152.188	0.316
				170.644	343.107	0.320
				218.253	40.308	0.028
	5	0.573	57, 90, 130, 156, 212	43.635	76.301	0.126	0.400
				72.881	99.772	0.138
				110.800	131.973	0.254
				142.590	55.391	0.220
				178.408	270.837	0.237
				219.035	38.368	0.025
PSO	1	1.023	66	47.900	114.220	0.168	0.034	0.373
				137.948	1446.983	0.832
	2	0.564	64, 137	47.023	104.922	0.159	0.060
				105.419	421.751	0.416
				168.426	564.154	0.424
	3	0.413	97, 140, 182	63.047	390.706	0.300	0.073
				119.448	154.217	0.300
				157.206	130.606	0.281
				201.012	152.773	0.119
	4	0.410	28, 89, 133, 169	22.825	17.056	0.007	0.091
				59.246	263.407	0.252
				112.179	160.043	0.284
				149.441	99.432	0.282
				192.596	259.838	0.175
	5	0.576	40, 70, 125, 159, 230	32.580	32.714	0.037	0.115
				53.830	68.546	0.146
				100.401	235.202	0.297
				141.671	92.691	0.281
				184.398	346.042	0.237
				234.122	19.797	0.002

The Lena image in which a random noise is generated will be our last test instance (Figure 16a), from this it is expected to provide clear evidence concerning robustness of the proposed method, where all the parameter values and computational results are summarized on Table 8. By observing the thresholded images when implementing the proposed approach (Figure 16b–d), we are able to conclude that random noise does not represent a major issue, even though different optimization tools are used.

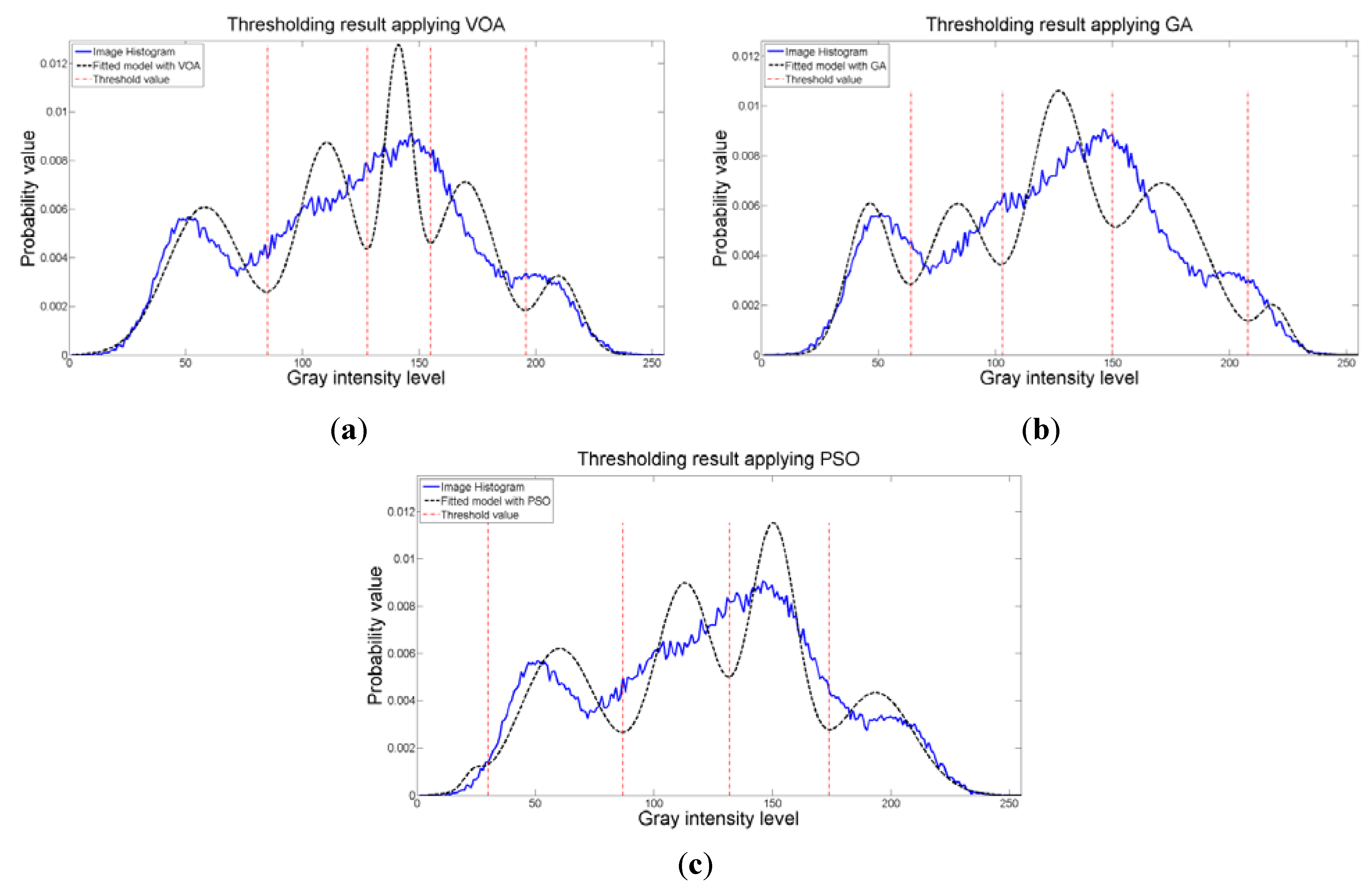
The objective function behavior (Figure 17c) proved once again that when a suitable number of thresholds is achieved, the addition of more distributions into the mixture model is not necessary, since it will always achieve a larger objective function value compared with the one given by having four thresholds (or five Gaussians). Additionally, the fitting of the histogram (Figure 18) given by the image, even though is not a perfect one, is proved to be good enough to keep most of the relevant details from the original test instance.

Most of the relevant details from the original instance are kept. On the other hand, Otsu’s method (Figure 16e) is not able to provide an output image as clear as the ones given by the proposed approach when implementing the meta-heuristic tools.

Figure 16. Test image 5: (a) Original image; Thresholded image implementing (b) VOA, (c) GA, (d) PSO, and (e) Otsu’s method with 4 thresholds.

Figure 16. Test image 5: (a) Original image; Thresholded image implementing (b) VOA, (c) GA, (d) PSO, and (e) Otsu’s method with 4 thresholds.

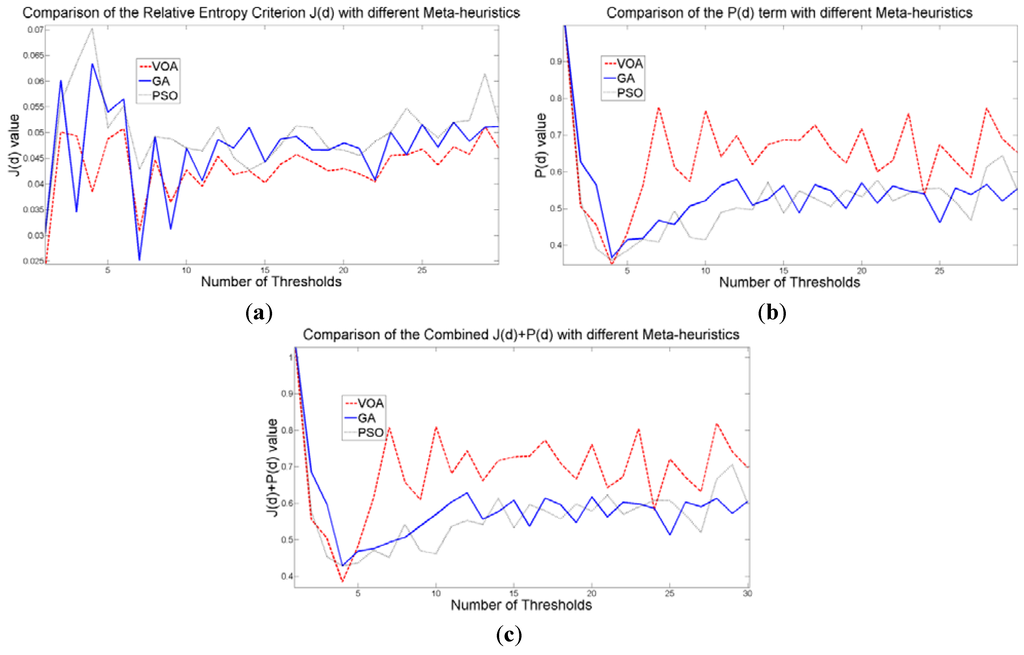
Figure 17. Behavior of (a) Relative Entropy function J(d), (b) P(d), and (c) Objective function Θ(d) over different numbers of thresholds with different meta-heuristics VOA, GA and PSO on test image 5.

Figure 17. Behavior of (a) Relative Entropy function J(d), (b) P(d), and (c) Objective function Θ(d) over different numbers of thresholds with different meta-heuristics VOA, GA and PSO on test image 5.

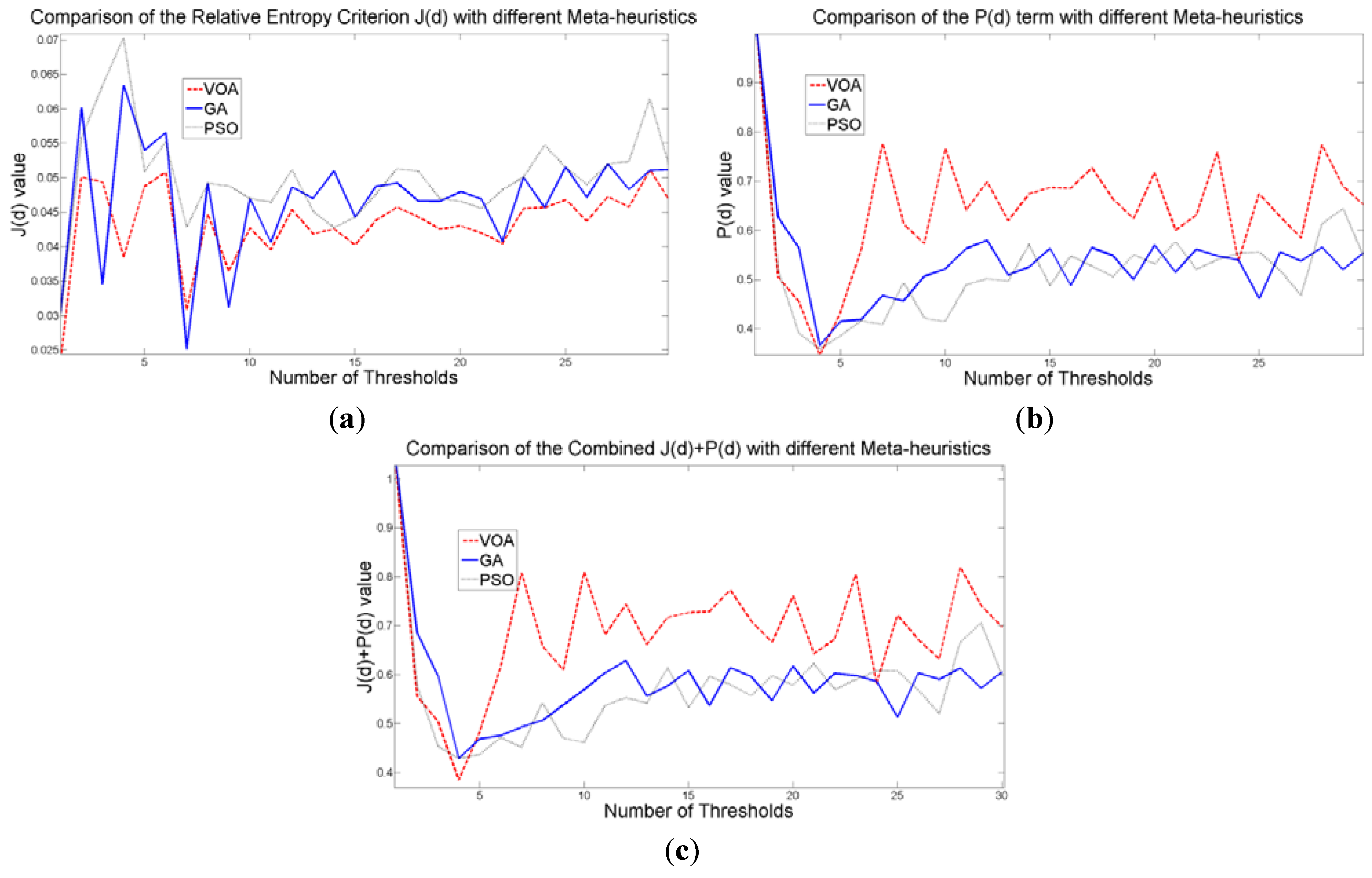
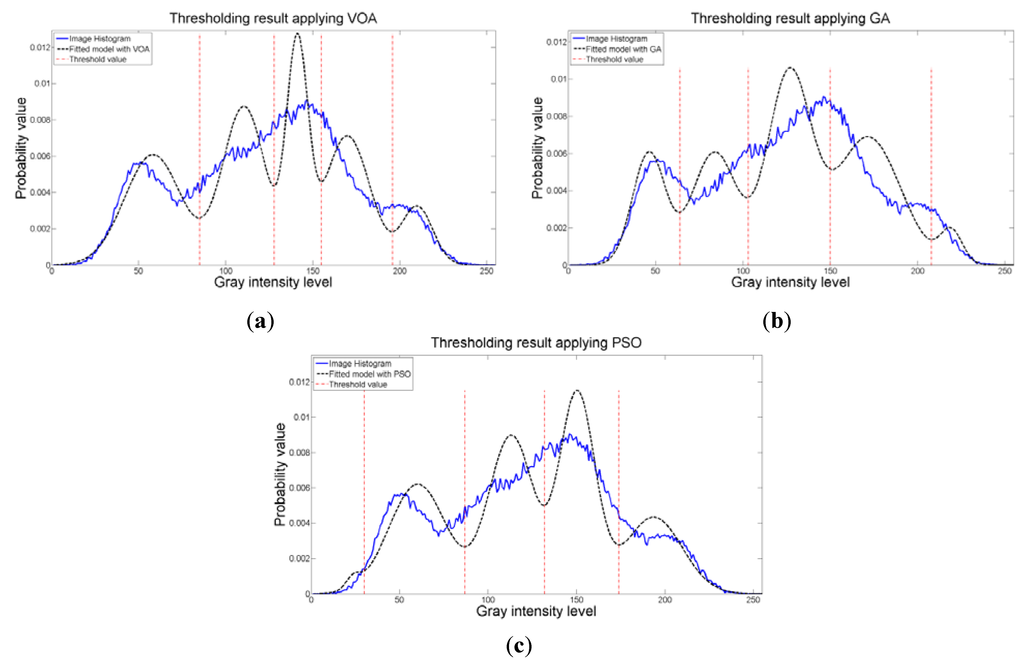
Figure 18. Fitting of the histogram of the test image 5 implementing (a) VOA, (b) GA, and (c) PSO.

Figure 18. Fitting of the histogram of the test image 5 implementing (a) VOA, (b) GA, and (c) PSO.

4. Conclusions

In this study a new approach to automatically assess the number of components “d” in a mixture of Gaussians distributions has been introduced. The proposed method is based on the Relative Entropy Criterion (Kullback-Leibler information distance) where an additional term is added to the function and helps to determine a suitable number of distributions. Finding the appropriate number of distributions is the same as determining the number of thresholds for segmenting an image, and this study has further shown that the method proposed in [8] is powerful enough in finding a suitable number of distributions (thresholds) in a short period of time.

The novelty of the approach is that, not only an appropriate number of distributions determined by P(d) is achieved, but also a good fitting of the image histogram is obtained by the Relative Entropy function J(d). The optimization of Equation (10) was performed implementing the Virus Optimization Algorithm, Genetic Algorithm, Particle Swarm Optimization, and the output images are compared to that given by a well-known segmentation approach Otsu’s method. The objective function behavior shows that the proposed model achieves a suitable number of thresholds when its minimum value is achieved, and the addition of more distributions (thresholds) into the model will cause an increasing trend of the model in Equation (10).

Comparing the proposed method with Otsu’s method provided clear evidence of the effectiveness and efficiency of the approach where the algorithmic tools are used in order to reduce the computational effort when optimizing Equation (10). Additionally, the proposed method proved to reach the same value for the number of thresholds needed for the segmentation of the images tested in this study, even though different optimization algorithms were implemented.

It is worth mentioning that the proposed method proved to work remarkably well under test images with low contrast and random noise. A suitable number of thresholds and an outstanding result in the output thresholded images were obtained. Whereas for the Otsu’s method, the output image showed some defects once the segmentation was performed.

The fitting result coming from the proposed approach might not be the best; however, when segmenting an image what matters the most is the fidelity in which most of the details are kept from the original picture. This is what makes the difference between a good and poor segmentation result. Future directions point toward testing the proposed method with more meta-heuristic algorithms, as well as a wider range of images to evaluate the robustness of the approach.