In order to evaluate the multivariate causality measures, the percentage of rejection of the null hypothesis of no causal effects () in 100 realizations of the system is calculated for each possible pair of variables and for different time series lengths and free parameters of the measures. The focus when presenting the results is on the sensitivity of the measure or, respectively, the power of the significance test (the percentage of rejection at the significance level or when there is true direct causality), as well as the specificity of the measure or size of the test (the percentage of rejection at when there is no direct causality) and how these properties depend on the time series length and the measure-specific parameter.
4.1. Results for System 1
For the estimation of the linear measures, the order of the model,
P, is set to one, as indicated from the Bayesian Information Criterion (BIC) and the Akaike Information Criterion (AIC), while for the estimation of PTE,
m is also set to one. The PDC is estimated for the range of frequencies
, since the auto-spectra of the variables do not suggest a narrower range. Indeed, the
p-values of PDC are all significant in
, when there is direct causality, and not significant, when there is no direct causality. The CGCI, PGCI, PDC and PTE correctly detect the direct causal effect for both time series lengths,
and 2048. All the aforementioned measures indicate
rejection of
for the true couplings,
and
, and low percentages for all other couplings. Their performance is not affected by the time series length, for the time series lengths considered. The estimated percentages are displayed for both
n in
Table 1.
The PSTE can only be estimated for , and therefore, results are obtained for . The PSTE correctly detects the direct causalities for ; however, it also indicates the indirect effect, , and the spurious causal effect, .
Only for this system, the PMIME with the threshold of
failed to detect the true direct effects, and the randomization test gave partial improvement (detection of one of the two true direct effects,
). This is merely a problem of using the fixed threshold,
, in this system, and following the adapted threshold proposed in [
28], the two true direct effects could be detected for all realizations with
and
with the largest rate of false rejection being
.
4.2. Results for System 2
For the second simulation system, the model order is set to
, as indicated both by BIC and AIC. The embedding dimension,
m, and
are also set to five. The PDC is estimated for the range of frequencies,
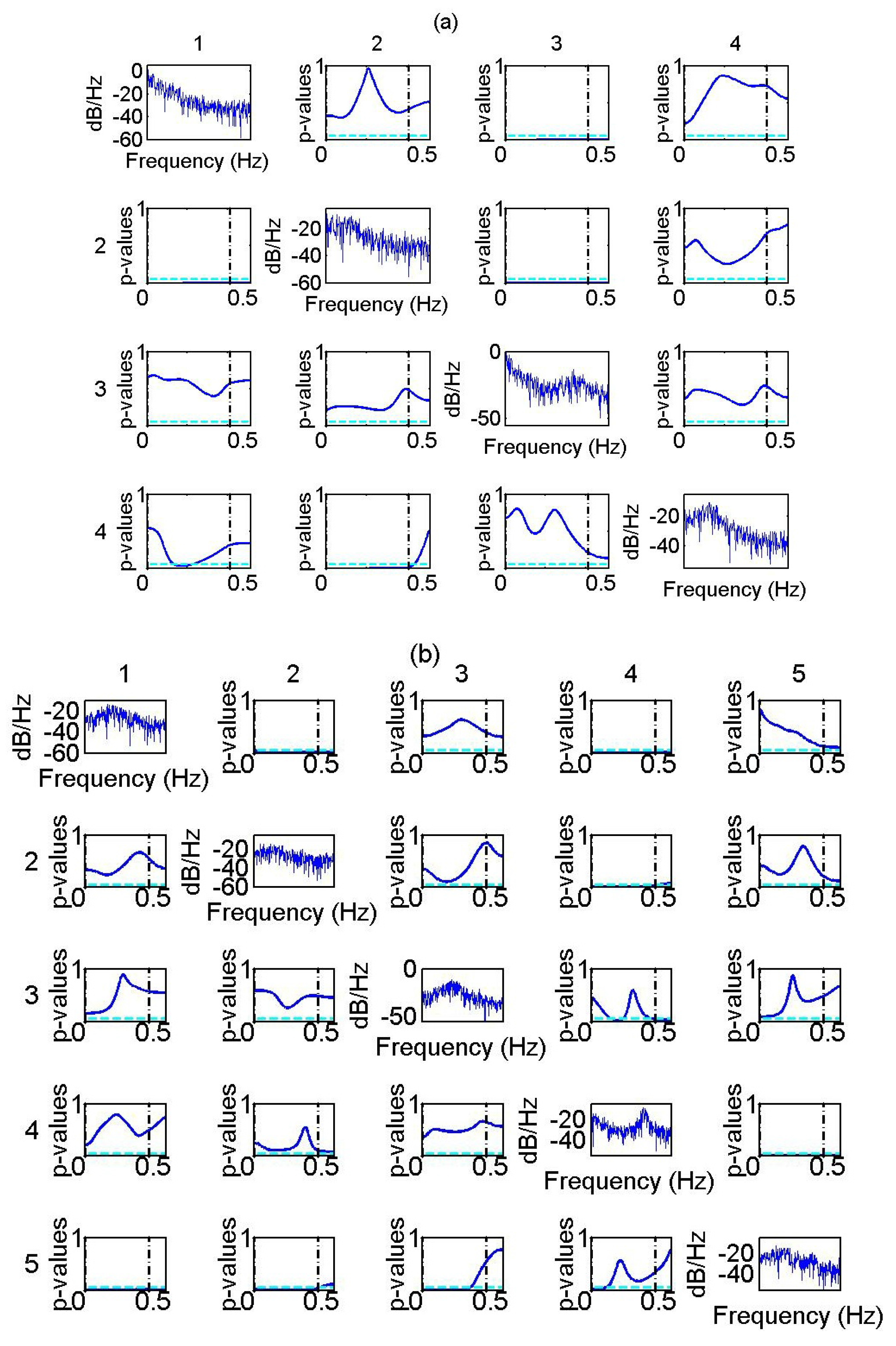
, since the auto-spectra of all the variables are higher in the range,
, while variable,
, exhibits a peak in the range,
. Indicatively, the
p-values from one realization of the system for the range of frequencies,
, is displayed in
Figure 1a.
The CGCI, PGCI, PDC and PMIME correctly detect the direct couplings (
,
,
,
), as shown in
Table 2. The performance of the CGCI and PDC is not affected by the time series length. The PGCI is also not affected by
n, except for the causal effect,
, where the PGCI falsely indicates causality for
(
). The PMIME indicates lower power of the test compared to the linear measures only for
and
.
The PTE detects the direct causal relationships, apart from the coupling,
, although the percentage of rejection in this direction increases with
n (from
for
to
for
). Further, the erroneous relationships,
(
) and
(
), are observed for
. Focusing on the PTE values, it can be observed that they are much higher for the directions of direct couplings than for the remaining directions. Moreover, the percentages of significant PTE values increase with
n for the directions with direct couplings and decrease with
n for all other couplings (see
Table 3).
We note that the standard deviation of the estimated PTE values from the 100 realizations are low (on the order of ). Thus, the result of having falsely statistically significant PTE values for and is likely due to insufficiency of the randomization test.
PSTE fails to detect the causal effects for the second coupled system for both time series lengths, giving rejections at a rate between and for all directions. The failure of PSTE may be due to the the high dimensionality of the rank vectors (the joint rank vector has dimension 21).
4.3. Results for System 3
The CGCI, PGCI, PDC, PTE and PMIME correctly detect all direct causal effects (
,
,
,
,
,
,
) for
=
(based on BIC and AIC), as shown in
Table 4.
The PDC is again estimated in the range of frequencies,
, (see in
Figure 1b the auto-spectra of the variables and the
p-values from the parametric test of PDC from one realization of the system). The CGCI, PGCI and PDC perform similarly for the two time series lengths. The PTE indicates
significant values for
when direct causality exists. However, the PTE also indicates the spurious causality,
, for
(
). The specificity of the PMIME is improved by the increase of
n, and the percentage of positive PMIME values in case of no direct causal effects varies from
to
for
, while for
, it varies from
to
. The PSTE again fails to detect the causal effects, giving very low percentage of rejection at all directions (
to
).
Since the linear causality measures CGCI, PGCI and PDC have been developed for the detection of direct causality in linear coupled systems, it was expected that these methods would be successfully applied to all linear systems. The nonlinear measures PMIME and PTE also seem to be able to capture the direct linear couplings in most cases, with PMIME following close the linear measures both in specificity and sensitivity.
In the following systems, we investigate the ability of the causality measures to correctly detect direct causal effects when nonlinearities are present.
4.4. Results for System 4
For the fourth coupled system, the BIC and AIC suggest to set , 2 and 3. The performance of the linear measures does not seem to be affected by the choice of P. The PDC is estimated for frequencies in . The auto-spectra of the three variables do not display any peaks or any upward/downward trends. No significant differences in the results are observed if a wider or narrower range of frequencies is considered. The linear measures, CGCI, PGCI and PDC, capture only the linear direct causal effect, , while they fail to detect the nonlinear relationships, and , for both time series lengths.
The PTE and the PMIME correctly detect all the direct couplings for the fourth coupled system for
, 2 and 3. The percentage of significant values of the causality measures are displayed in
Table 5. The PTE gives equivalent results for
and
. The PTE correctly detects the causalities for
, but at a smaller power of the significance test for
(
for
,
for
and
for
). The percentage of significant PMIME values is
for the directions of direct couplings, and falls between
and
for all other couplings, and this holds for any
, 2 or 3 and for both
n.
The PSTE indicates the link for both time series lengths, while is detected only for . The PSTE fails to point out the causality, . The results for and 3 are equivalent. In order to investigate whether the failure of PSTE to show is due to finite sample data, we estimate the PSTE also for . For , it indicates the same results as for . For , the PSTE detects all the direct causal effects, (), (), (), but () is also erroneously detected.
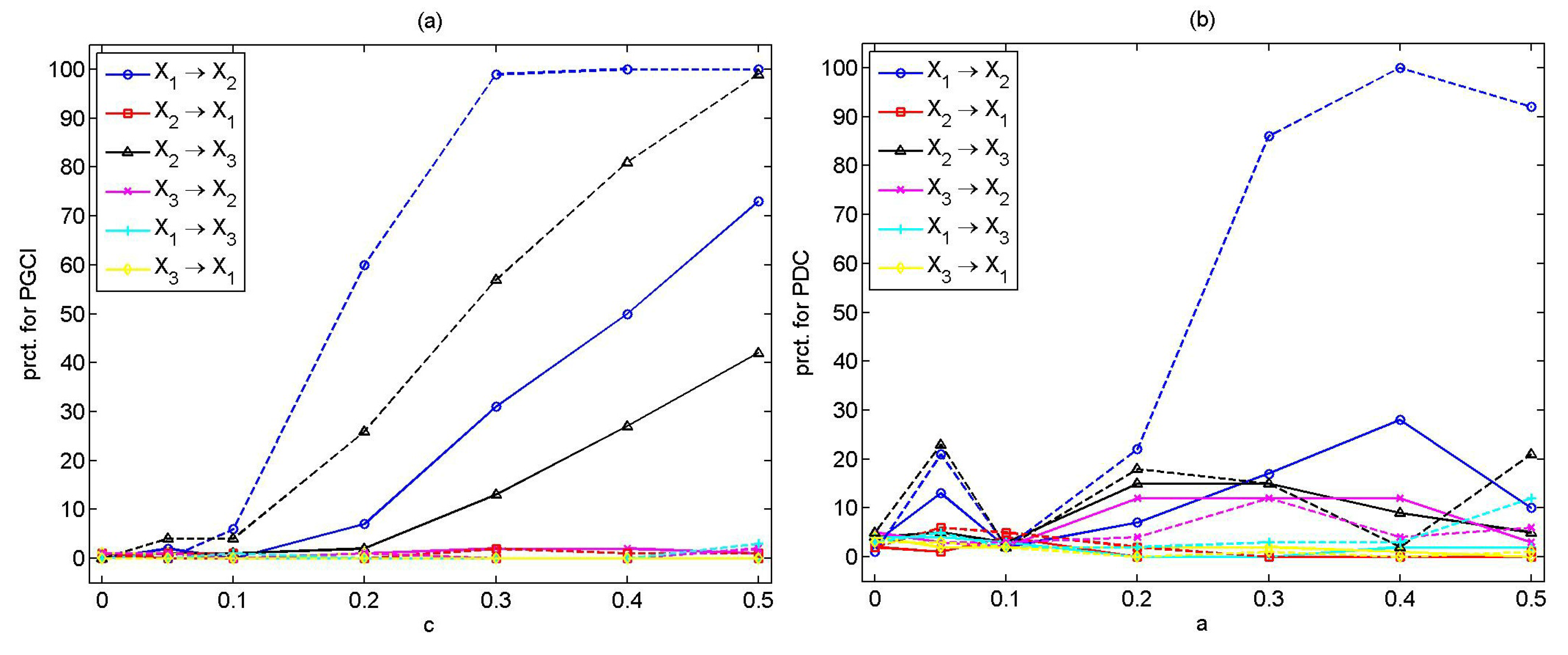
4.5. Results for System 5
For the fifth coupled simulation system, we set the model order, , based on the complexity of the system, and and 5 using the AIC and BIC. The auto-spectra of the variables display peaks in and . The PDC is estimated for different ranges of frequencies to check its sensitivity with respect to the selection of the frequency range. When small frequencies are considered, the PDC seems to indicate larger percentages of spurious couplings; however, also, the percentages of significant PDC values at the directions of true causal effects are smaller. The results are presented for System 5 considering the range of frequencies, .
The CGCI seems to be sensitive to the selection of the model order
P, indicating some spurious couplings for the different
P. The best performance for CGCI is achieved for
; therefore, only results for
are shown. On the other hand, the PGCI turns out to be less dependent on
P, giving similar results for
, 3, 4 and 5. The PTE is not substantially affected by the selection of the embedding dimension,
m (at least for the examined coupling strengths); therefore, only results for
are discussed. The PSTE is sensitive to the selection of
m, performing best for
and 3, while for
and 5, it indicates spurious and indirect causal effects. The PMIME does not seem to depend on
. Results are displayed for
. The percentage of significant values for each measure are displayed in
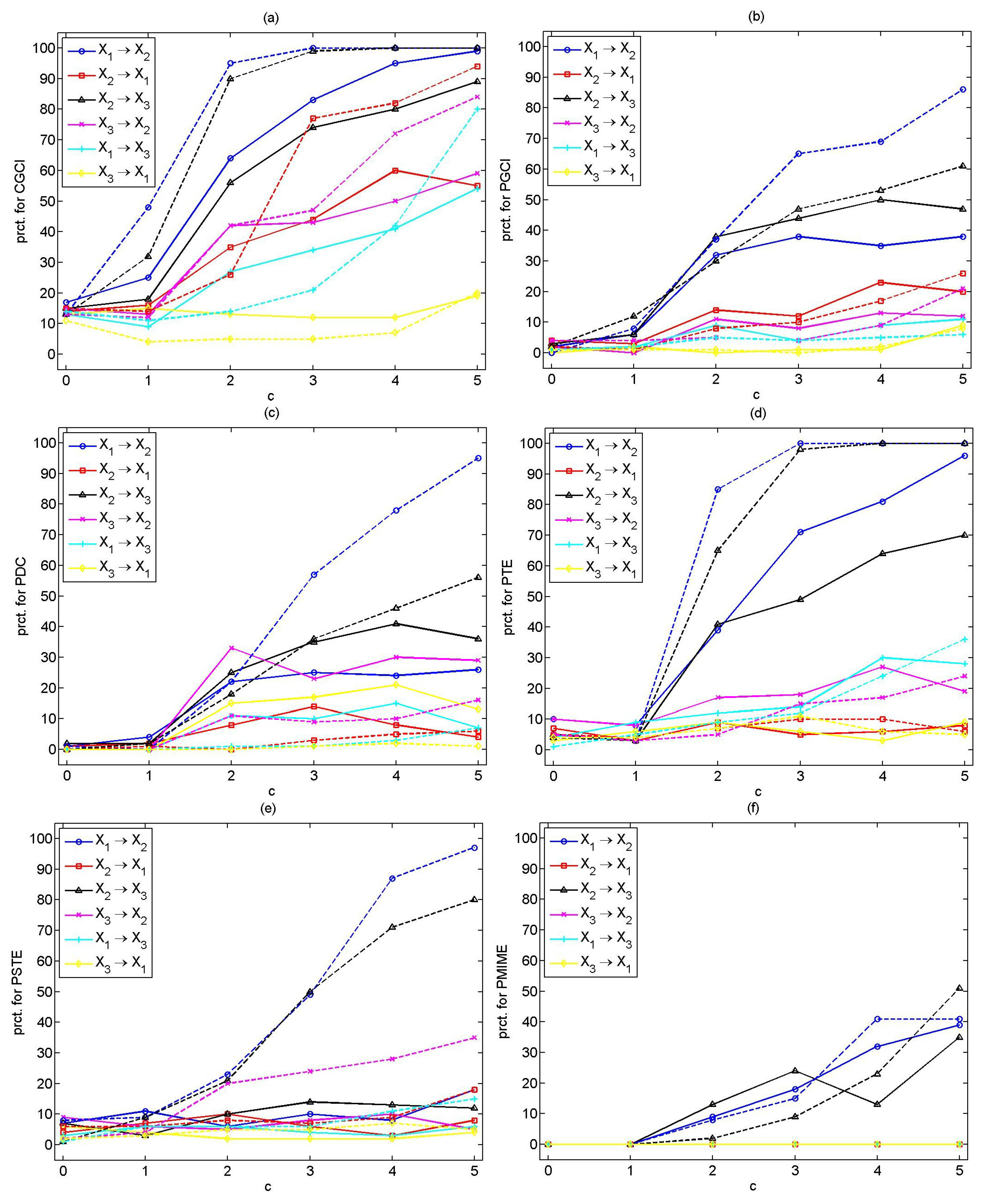
Figure 2, for all directions, for increasing coupling strength and for both
n.
Most of the measures show good specificity, and the percentage of rejection for all pairs of the variables of the uncoupled system () is at the significance level, , with only CGCI scoring a somehow larger percentage of rejection up to .
For the weak coupling strengths, and 0.1, the causality measures cannot effectively detect the causal relationships or have a low sensitivity. The CGCI and the PTE seem to have the best performance, while the PMIME seems to be effective only for and .
As the coupling strength increases, the sensitivity of the causality measures is improved. For
, the CGCI, PTE and PMIME correctly indicate the true couplings for both
n, while the PGCI and the PSTE do this only for
. The PDC has low power, even for
. For
, nearly all measures correctly point out the direct causal effects (see
Table 6). The best results are obtained with the PMIME, while the CGCI and PTE display similar performance. The PGCI and the PSTE are sensitive to the time series length and have a high power only for
. The PDC performs poorly, giving low percentage of significant PDC values, even for
. All measures have good specificity, with CGCI and PTE giving rejections well above the nominal level for some non-existing couplings.
Considering larger coupling strengths, the causality measures correctly indicate the true couplings, but also some spurious ones. The PMIME outperforms the other measures giving
positive values for both
n for
and
and
at the remaining directions for
. Indicative results for all measures are displayed for the strong coupling strength
in
Table 7.
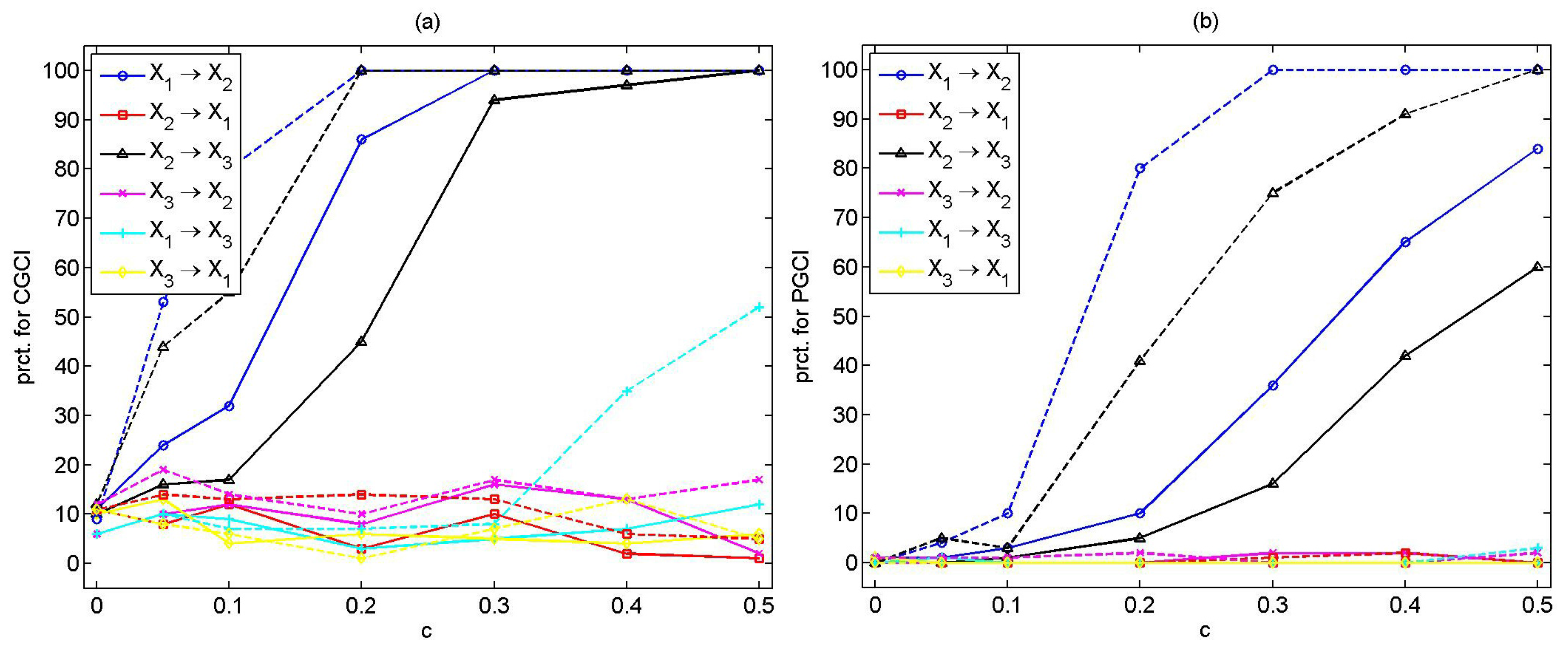
In order to investigate the effect of noise on each measure, we consider the coupled Hénon map (System 5) with the addition of Gaussian white noise with standard deviation times the standard deviation of the original time series. Each measure is estimated again from 100 realizations from the noisy system for the same free parameters as considered in the noise-free case.
The CGCI is not significantly affected by the addition of noise, giving equivalent results for as for the noise-free system. The CGCI detects the true causal effects even for weak coupling strength (). For different P values ( or 5), some spurious and/or indirect causal effects are observed for .
The PGCI is also not considerably affected by the addition of noise. The causal effects are detected only for coupling strengths,
, for
, and for
, for
, while the power of the test increases with
c and with
n (see
Figure 3a).
The PDC fails in the case of the noisy coupled Hénon maps, detecting only the coupling
, for coupling strengths,
and
(see
Figure 3b).
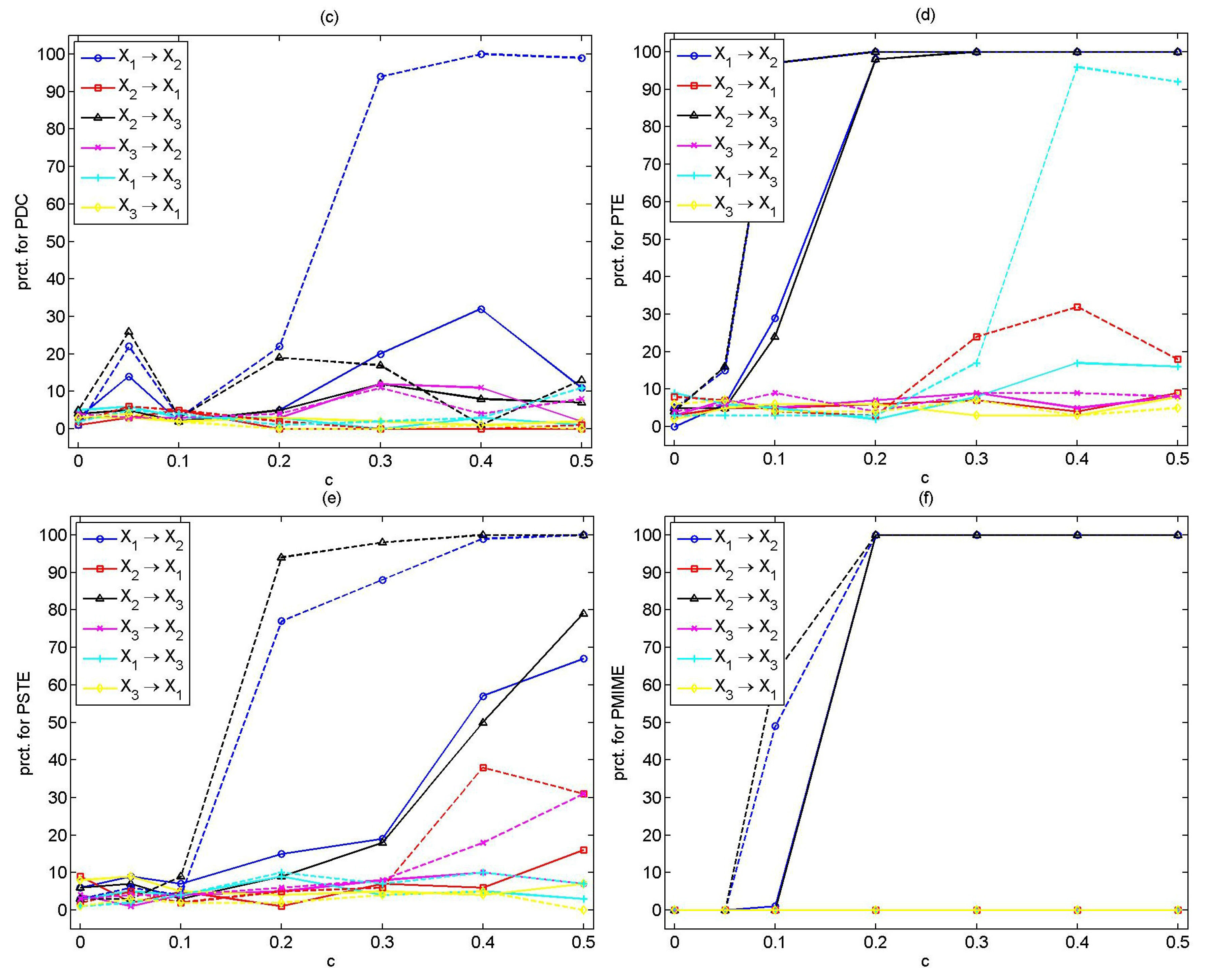
The PTE seems to be significantly affected by the addition of noise, falsely detecting the coupling,
,
, and the indirect coupling,
, for strong coupling strengths. The performance of PTE is not significantly influenced by the choice of
m. Indicative results are presented in
Table 8 for
.
Noise addition does not seem to affect the performance of PSTE. Results for are equivalent to the results obtained for the noise-free case. The power of the significance test increases with c and n. The PSTE is sensitive to the selection of m; as m increases, the percentage of significant PSTE values in the directions of no causal effects also increases.
The PMIME outperforms the other measures also for the noisy coupled Hénon maps, detecting the true couplings for for () and for for (for coupling strength the percentages are and for , , respectively, and for , the percentages are , for both couplings).
4.6. Results for System 6
For System 6, we set
based on the complexity of the system and
regarding the AIC and BIC. The PTE, PSTE and PMIME are estimated for four different combinations of the free parameters,
h and
m (
for PMIME),
i.e., for
and
, for
and
, for
and
and for
and
. The PDC is computed for the range of frequencies,
, based on the auto-spectra of the variables. As this system is a nonlinear flow, the detection of causal effects is more challenging compared to stochastic systems and nonlinear coupled maps. Indicative results for all causality measures are displayed for increasing coupling strengths in
Figure 4.
The CGCI has poor performance, indicating many spurious causalities. The PGCI improves the specificity of the CGCI, but still, the percentages of statistically significant PGCI values increase with c for non-existing direct couplings (less for larger n). Similar results are obtained for and 5. On the other hand, the PDC is sensitive to the selection of P, indicating spurious causal effects for all P. As P increases, the percentage of significant PDC values at the directions of no causal effects is reduced. However, the power of the test is also reduced.
The PTE is sensitive to the embedding dimension m and the number of steps ahead h, performing best for and . It fails to detect the causal effects for small c; however, for , it effectively indicates the true couplings. The size of the test increases with c (up to for and ), while the power of the test increases with n.
The PSTE is also affected by its free parameters, performing best for and . It is unable to detect the true causal effects for weak coupling strengths () and for small time series lengths. The PSTE is effective only for and . Spurious couplings are observed for strong coupling strengths c and .
The PMIME is also influenced by the choice of h and , indicating low sensitivity when setting , but no spurious couplings, while for , the percentage of significant PMIME values for and is higher, but the indirect coupling is detected for strong coupling strengths. The PMIME has a poor performance for weak coupling strength ().
As
c increases, the percentages of significant values of almost all the causality measures increase, but not only at the true directions,
and
. Indicative results are presented in
Table 9 for strongly coupled systems (
). The CGCI gives high percentages of rejection of
for all couplings (very low specificity). This also holds for the PGCI, but at a lower significance level. The PTE correctly detects the two true direct causal effects for
and
, but at some significant degree, also the indirect coupling,
, and the non-existing coupling,
. The PSTE does not detect the direct couplings for
, but it does when
(
for
and
for
), but then it detects also spurious couplings, most notably
(
). The PMIME points out only the direct causal effects, giving, however, a lower percentage than the other measures for
,
. Its performance seems to be affected by the selection of
h and
. The nonlinear measures turn out to be more sensitive to their free parameters.
4.7. Results for System 7
For the last coupled simulation system, we set the model order
, 3, 4 based on AIC and BIC, while the PDC is estimated in the range of frequencies,
. The embedding dimension,
m, for the estimation of PTE and PSTE, as well as
for the estimation of PMIME, are set equal to
P. Results for all causality measures are displayed in
Table 10.
The CGCI (for ) correctly indicates the causal effects for , giving percentage of significant values at the direction and , but lower percentage at the directions (), () and (). The power of the test increases with n, but spurious couplings are also detected for . For , 3 and 4, the CGCI indicates more spurious couplings than for .
System 7 favors the PGCI, as it has been specifically defined for systems with latent and exogenous variables. The PGCI denotes the couplings, , , and , even for with a high percentage; however, it fails to detect the coupling, , for both n.
The PDC detects the true couplings at low percentage for . The percentage increases with at the directions of the true couplings. However, there are also false indications of directed couplings.
The PTE does not seem to be effective in this setting for any of the considered m values, since it indicates many spurious causal effects, while it fails to detect . The PSTE completely fails in this case, suggesting significant couplings at all directions. The true causal effects are indicated by the PMIME, but here, as well, many spurious causal effects are also observed.