Abstract
DNA computing based image encryption is a new, promising field. In this paper, we propose a novel image encryption scheme based on DNA encoding and spatiotemporal chaos. In particular, after the plain image is primarily diffused with the bitwise Exclusive-OR operation, the DNA mapping rule is introduced to encode the diffused image. In order to enhance the encryption, the spatiotemporal chaotic system is used to confuse the rows and columns of the DNA encoded image. The experiments demonstrate that the proposed encryption algorithm is of high key sensitivity and large key space, and it can resist brute-force attack, entropy attack, differential attack, chosen-plaintext attack, known-plaintext attack and statistical attack.
1. Introduction
With the rapid development of Internet and communication technologies, image communication plays a very important role in information transmission, and thus the image encryption has attracted more and more attention. Digital images have intrinsic properties that are different from texts, such as bulk data capacity and strong correlation among pixels, which make some traditional data encryption techniques are not very suitable for digital image encryption [1,2]. Therefore, some interesting and promising theories, such as chaos [1,2] and phase retrieval algorithm [3,4], have been applied in the image encryption.
Chaos has many good properties, such as ergodicity, high sensitivity to initial conditions and control parameters, and low computational complexity, so the chaos has been shown significant potential in digital image encryption. Since Matthews [5] suggested that a one-dimensional chaotic map could be used as one time pad for encrypting messages, various image encryption algorithms based on the chaotic systems have been proposed. Pareek [6] introduced an image encryption approach based on two chaotic Logistic maps, in which the initial condition of the second Logistic map was modified from the numbers generated by the first Logistic map. Wang [7] developed a color image encryption based on the Logistic map. Liu [8] presented the image encryption based on one-time keys and two robust chaotic maps. Wang [9] introduced an encryption algorithm by using high-dimension Lorenz chaotic system and perceptron model. Liu [10] proposed a color image encryption method by combining spatial bit-level permutation and high-dimension chaotic system.
It has been demonstrated that the communication with the spatiotemporal chaos based on coupled map lattice (CML) is more secure than that with a single map [10]. The spatiotemporal chaotic system possesses much better properties than the simple chaotic system, such as larger parameter space, more positive Lyapunov exponents, higher randomness and more chaotic sequences, so that it is more difficult to predict the chaotic series generated by the spatiotemporal chaotic systems. Therefore, the spatiotemporal chaos is more suitable for data protection. However, the CML system is often based on the mapping function f(x) = μx(1 − x) and μ ∈ (0, 4]. The parameter μ still has periodic windows in the bifurcation diagram of some lattice, so the range of parameter μ is much smaller than (0, 4] [10]. Thus, the NCA (Nonlinear Chaotic Algorithm) map based spatiotemporal chaos [11] is introduced for the image encryption.
Since Adleman studied the DNA computing to solve the combinational problem [12], the DNA computing technique has attracted more attention. In recent years, DNA technology has been applied to cryptography field due to its excellent characteristics such as massive parallelism, huge storage and ultra-low power consumption [13,14,15]. DNA cryptogram utilizes DNA as information carrier and takes the advantage of biological technology, which has been shown promising results in the image encryption. Gehani et al. [16] presented a DNA-based cryptography based on one-time-pads that are in principle unbreakable. Because such experiments need nature DNA sequences to encoding the information, it can only be done in a well-equipped lab and needs high cost. Zhang et al. [17] proposed an image encryption scheme by combining the chaotic system with the DNA sequence addition operation and complement operation, in which the chaotic sequence is generating by the Logistic map. Liu [15] developed an image encryption method using DNA complementary rule and piecewise linear chaotic map. These results demonstrated that the good encryption result could be achieved with DNA computing.
Taking the advantages of spatiotemporal chaos and DNA computing into account, the paper proposes an image encryption algorithm using the spatiotemporal chaotic system based on NCA map and the DNA complementary rule. The rest of this paper is organized as follows. The related works are presented in Section 2. Section 3 introduces the proposed image encryption algorithm. The experimental results and security analysis are conducted in Section 4 and Section 5 respectively. Finally, the conclusions are drawn in the last section.
2. Related Work
2.1. DNA Coding and Complementary Rule
A DNA sequence contains four nucleic acid bases A (Adenine), C (Cytosine), G (Guanine) and T (Thymine), where A and T, C and G are complementary pairs. In the binary system, 0 and 1 are complementary, 00 and 11, 10 and 01 also are complementary. If 00, 11, 10 and 01 are encoded with nucleic acid bases A, C, G and T, we can get 4!= 24 kinds of encoding schemes. Due to the complementary relation between DNA bases, there are eight kinds of encoding combinations satisfying the principle of complementary base pairing, which are shown in Table 1.

Table 1.
Eight kinds of DNA map rules.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| A | 00 | 00 | 01 | 01 | 10 | 10 | 11 | 11 |
| T | 11 | 11 | 10 | 10 | 01 | 01 | 00 | 00 |
| G | 01 | 10 | 00 | 11 | 00 | 11 | 01 | 10 |
| C | 10 | 01 | 11 | 00 | 11 | 00 | 10 | 01 |
For a grayscale image, each 8 bit pixel value can be encoded into a nucleotide string whose length is 4. For example, there is a pixel with the grayscale value 148 that can be converted into a binary sequence “10010100”, if the DNA encoding rule 1 is adopted, the binary sequence can be expressed as the DNA sequence “CGGA”. Inversely, the DNA sequence can be decoded into a pixel value. When the wrong DNA encoding rule, for example, the rule 8 (the last column of Table 1), is used to decode the DNA sequence “CGGA”, we get the wrong binary sequence “01101011”, and then the wrongly decoding grayscale value 107. This method can be applied to the image encryption algorithm to achieve the image diffusion.
2.2. NCA Map
The NCA map is constructed on the basis of Logistic map. Logistic map is defined as
where 0 < μ ≤ 4, xn ∈ (0, 1). When 3.57 ≤ μ < 4, the map appears chaotic behavior. By introducing the power function and tangent function in the Logistic map, Gao [18] proposed a NCA map
where xn ∈ (0, 1), α ∈ (0, 1.4], β ∈ [5, 43], or xn ∈ (0, 1), α ∈ (1.4, 1.5], β ∈ [9, 38], or xn ∈ (0, 1), α ∈ (1.5, 1.57], β ∈ [3, 15]. The NCA map is a chaotic system with good properties of balanced 0–1 ratio, zero co-correlation and ideal nonlinearity.
2.3. Spatiotemporal Chaotic System
The two-way coupled map lattice system can be defined as
where i = 1, 2, …, L is the lattice site index, n = 1, 2, … is the time index, ε ∈ (0, 1) is a coupling constant, and xn(i) ∈ (0, 1). Here f(x) is the Logistic map with 3.57 ≤ μ< 4, 0 < x < 1 and 0 < f(x) < 1. The periodic boundary condition is xn(0) = xn(L).
Song [11] replaces the Logistic map in Equation (3) with the NCA map, and then the CML is
Figure 1 shows the spatiotemporal chaos with L = 1024, ε = 0.3, α = 1.57 and β = 3.5. We can see from Figure 1 that the system exhibits chaotic properties both in the time and space domains.
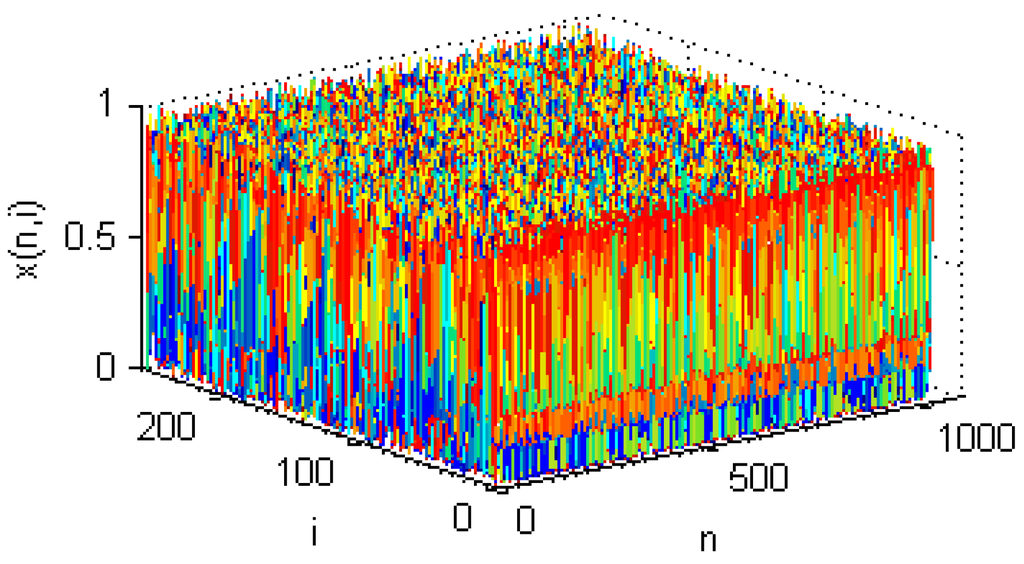
Figure 1.
Spatiotemporal chaos.
Figure 1.
Spatiotemporal chaos.
Lyapunov exponents provide a qualitative evaluation of the dynamical system. A dynamical system with chaotic behavior possesses at least one positive Lyapunov exponent. The Kolmogorov-Sinai entropy density h of a spatiotemporal chaotic system is the sum of positive Lyapunov exponents. The positive value of Kolmogorov-Sinai entropy density indicates the system in chaotic behavior [19,20]. Without loss of generality, we set the size of lattices L = 100 in the CML system for determining Kolmogorov-Sinai entropy densities, which are shown in Figure 2 for different spatiotemporal chaos maps. The results suggest that the spatiotemporal chaos based on CML and NCA is suitable for image encryption.
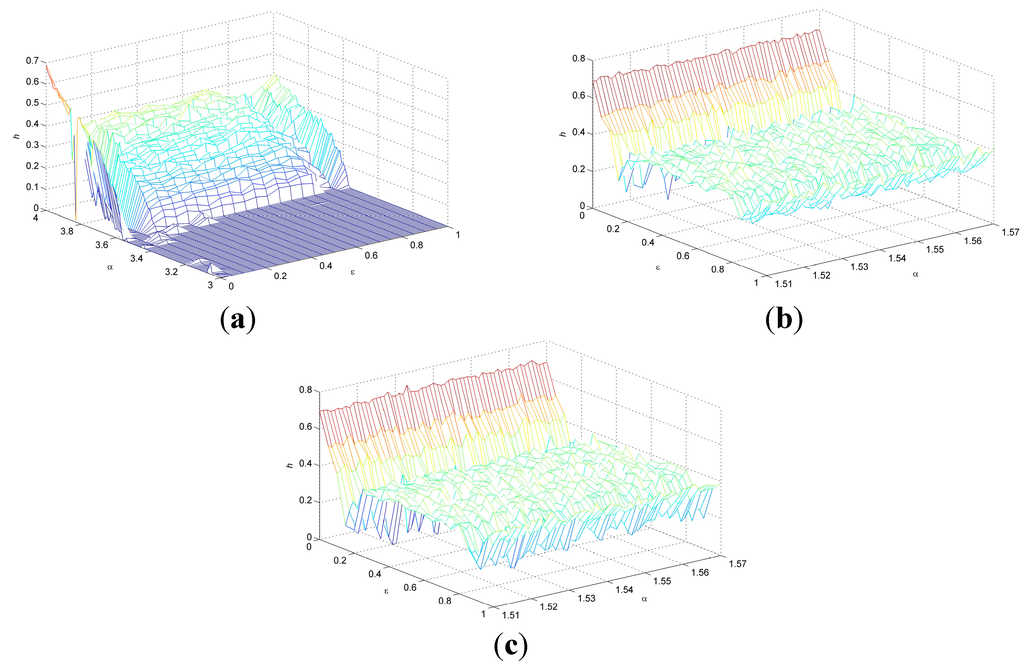
Figure 2.
Kolmogorov-Sinai entropy densities. (a) Spatiotemporal chaos based on Logistic chaos; (b) Spatiotemporal chaos based on an NCA map (α =1.51 to 1.57, β = 3.2); (c) Spatiotemporal chaos based on NCA map (α =1.51 to 1.57, β = 3.5).
Figure 2.
Kolmogorov-Sinai entropy densities. (a) Spatiotemporal chaos based on Logistic chaos; (b) Spatiotemporal chaos based on an NCA map (α =1.51 to 1.57, β = 3.2); (c) Spatiotemporal chaos based on NCA map (α =1.51 to 1.57, β = 3.5).
3. Proposed Image Encryption Algorithm
The proposed image encryption algorithm is based on the spatiotemporal chaotic system and the DNA complementary rule. The plain image is diffused with the bitwise Exclusive-OR operation, and then the diffused image is encoded with the DNA mapping rule. According to the sequence generated by the spatiotemporal chaotic system, the DNA encoded image is confused again. Finally, the cipher image is obtained after the DNA decoding. Therefore, The introduced method provides a secure encryption scheme by using the bitwise Exclusive-OR operation based diffusion, DNA encoding controlled with Logistic chaos, and the spatiotemporal chaos based DNA sequence confusion, in which the spatiotemporal chaos maps and DNA encoding improves the security, compared with the traditional algorithm. The introduced image encryption scheme is shown in Figure 3.
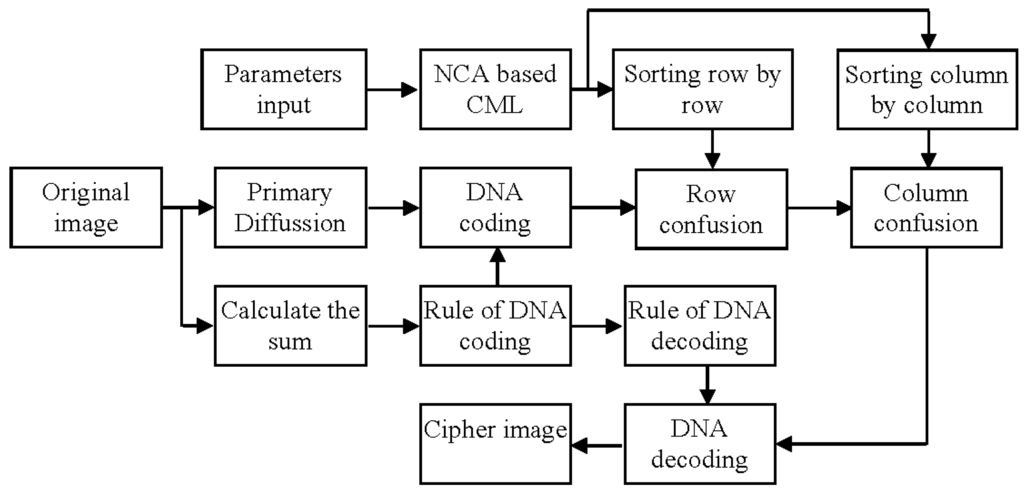
Figure 3.
Image encryption scheme.
Figure 3.
Image encryption scheme.
Without loss of generality, we assume that the size of a plain image is W × H. The proposed image encryption algorithm can be summarized as follows.
Step 1: Convert the image matrix M into a one-dimensional array , and then diffuse the array A according to the following formula,
where ⊕ is the bitwise Exclusive-OR (XOR) operation. We get the diffused array . Convert A′ to a matrix M′ with the size of W × H.
Step 2: x0 is adopted as the initial value of the Logistic map. Choose the K0th element x(K0) from the Logistic map sequence, and get an integer IDNA = floor(x(K0) × 8) that belongs to [0, 7]. According to IDNA we can determine the rule of DNA encoding. For example, IDNA = 0 corresponds to the first DNA mapping rule in Table 1, and IDNA = 1 corresponds to the second DNA mapping rule, and so on.
Step 3: Convert the matrix M′ to a binary value matrix M″ with the size of W × 8H. Encode the primary diffused matrix M″ with the selected DNA mapping rule in Step 2, and thus we get a encoded matrix MD with the size of W × 4H.
Step 4: Choose the (N0+1)-th element to the (N0+4H)-th element from the Logistic chaotic sequence in order to avoid the harmful effect of the transition procedure, and form a new sequence , which is adopted as the initial values of the spatiotemporal chaos. Generate the spatiotemporal chaotic matrix X with size of W × 4H according to Equation (4).
Step 5: Sort each row of X in ascending order, and then we obtain W position sequences , whose element RIXn(i) is the position where the i-th sorted element is located in the n-th row of the chaotic matrix X. Permute each row of the DNA encoded matrix MD according to RIXn, and get the confused matrix MD′ (, , ).
Step 6: Sort each column of X in ascending order and obtain 4H position sequences in a similar way as Step 5. Then confuse columns of the matrix MD′, and get a matrix MD′′ , , ).
Step 7: Calculate to determine the DNA decoding rule, with which the matrix MD′′ is decoded into a binary value matrix with the size of W × 8H. Finally, the binary matrix is converted to a gray scale image C with the size of W × H.
Output: Cipher image C.
The decryption process is the inverse process of the encryption.
4. Experimental Results
In this section, we evaluate the performance of the proposed image encryption algorithm. Three benchmark gray scale images with the size of 256 × 256 are shown in the first column of Figure 4. When KEY = {0.6434179, 3.7, 50, 1.57, 3.5, 0.3, 1024, 100}, the encrypted images are listed in the second column of Figure 4. The third column gives the decrypted images. From the decrypted results, we can see that the plain-image can be decrypted without distortion.

Figure 4.
Experimental results. (a) Plain image Lenna; (b) Cipher image of (a); (c) Decrypted image of (b); (d) Plain image Peppers; (e) Cipher image of (d); (f) Decrypted image of (e); (g) Plain image Boats; (h) Cipher image of (g); (i) Decrypted image of (h).
Figure 4.
Experimental results. (a) Plain image Lenna; (b) Cipher image of (a); (c) Decrypted image of (b); (d) Plain image Peppers; (e) Cipher image of (d); (f) Decrypted image of (e); (g) Plain image Boats; (h) Cipher image of (g); (i) Decrypted image of (h).

5. Security Analysis
5.1. Gray Histogram Analysis
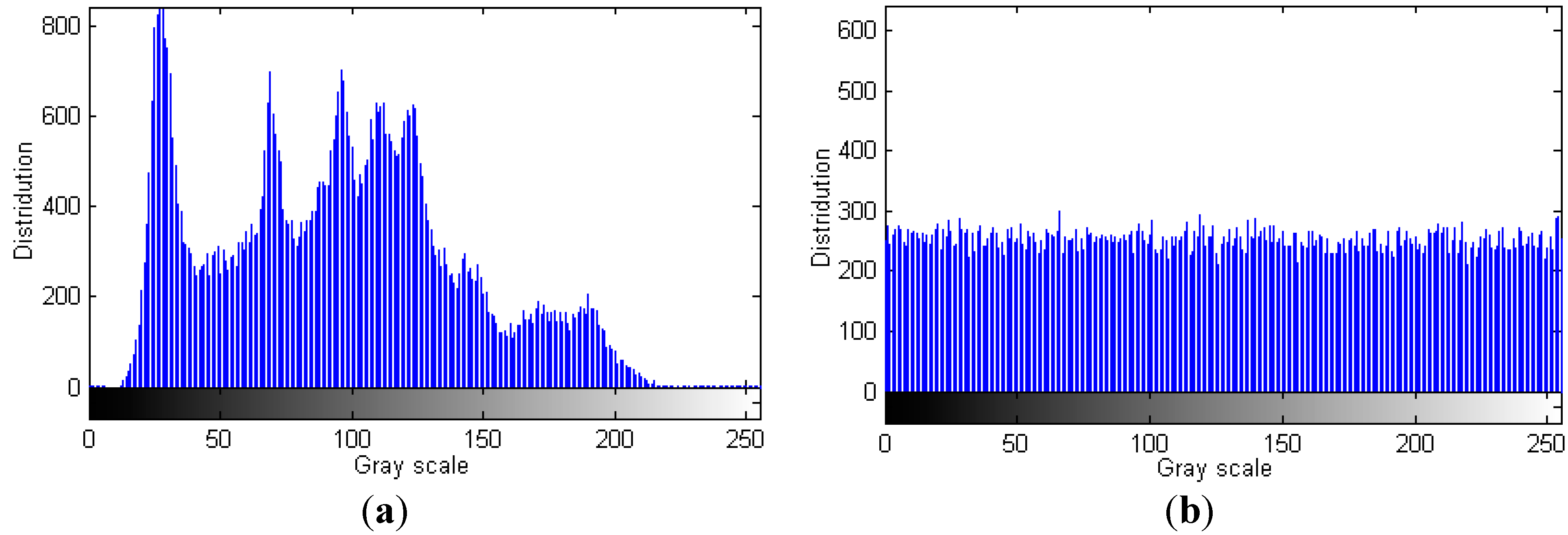
Histogram can reflect the information distribution of pixel values of an image. The histogram of the cipher image should be uniform enough to resist statistical attack, and otherwise the attackers may deduce useful information of the plain image by analyzing the histogram of the encrypted image [21]. Figure 5a shows the histogram of the plain image “Lenna” shown in Figure 4a, and the histogram of the cipher image shown in Figure 4b is given in Figure 5b. From Figure 5 we can see that the histogram of the cipher image becomes fairly uniform.
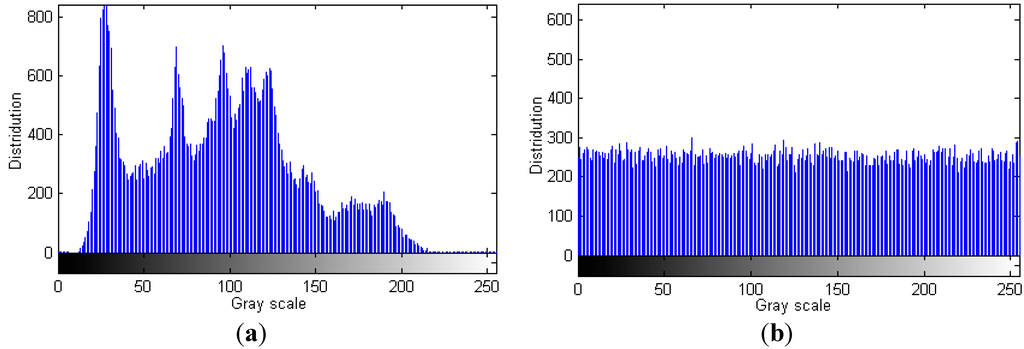
Figure 5.
Histogram analysis. (a) Histogram of the plain image; (b) Histogram of the cipher image.
Figure 5.
Histogram analysis. (a) Histogram of the plain image; (b) Histogram of the cipher image.
5.2. Information Entropy Analysis
Information entropy is an important feature of randomness. Based on Shannon’s theory [22], the entropy of a source s is defined as follows,
where P(si) represents the probability of symbol si, and N is the number of bits to represent symbol si∈s. According to the equation we can get the ideal entropy for a random image with 256 gray levels is 8. For the image “Lenna”, the entropy of the encrypted image shown in Figure 4b is 7.9967, which is close to 8 and demonstrates that the cipher image is close to a random image. We also conduct the entropy analysis on other benchmark images, and the calculated results are listed in Table 2, which are very close to the theoretical value of 8 and higher than many existing algorithms [23,24]. This means that the information leakage in the encryption process is very little, and the image encryption scheme is secure enough to resist the entropy attack.

Table 2.
Results of information entropy analysis.
| Lenna | House | Couple | Airplane | Peppers | Camera | Aerial | Boats | |
|---|---|---|---|---|---|---|---|---|
| Entropy | 7.9967 | 7.9933 | 7.9975 | 7.9974 | 7.9973 | 7.9958 | 7.9974 | 7.9973 |
5.3. Correlation Analysis
Randomly select 1000 pairs of adjacent pixels in horizontal, vertical and diagonal directions from the plain image and cipher image respectively, and calculate the correlation coefficients according to the following formula:
where xi and yi are gray values of two adjacent pixels, and N denotes the number of selected pixel pairs. The correlation distributions of adjacent pixels of plain image “Lenna” along horizontal, vertical and diagonal directions are shown in Figure 6a,c,e, respectively, and Figure 6b,d,f give the corresponding distributions of the cipher image. The correlation coefficients of adjacent pixels along different directions for different bench mark images are listed in Table 3. The results suggest that the strong correlations of adjacent pixels of the plain image are greatly reduced in the cipher image. The comparison results are shown in Table 4, from which it can be seen that our method is almost better than some existing algorithms.
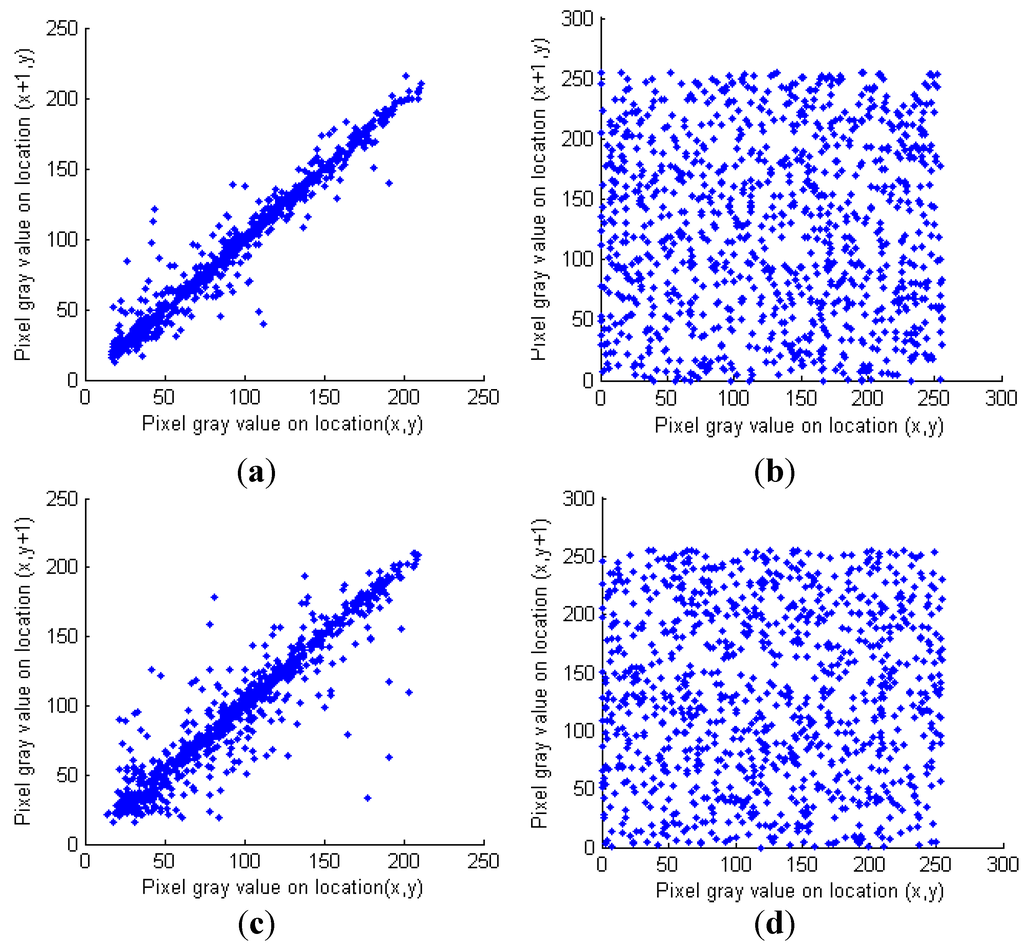
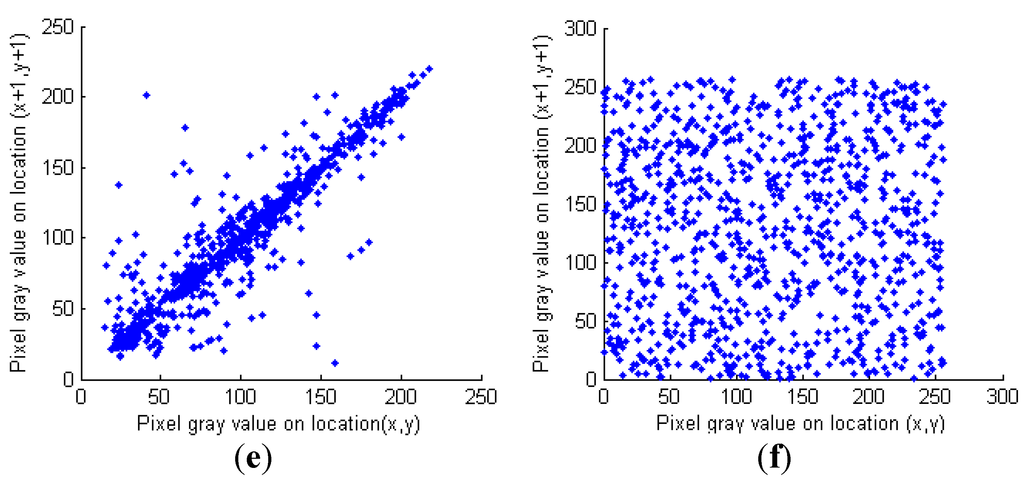
Figure 6.
Correlation analysis. (a) Correlation distribution of the plain image along the horizontal direction; (b) Correlation distribution of the encrypted image along the horizontal direction; (c) Correlation distribution of the plain image along the vertical direction; (d) Correlation distribution of the encrypted image along the vertical direction; (e) Correlation distribution of the plain image along the diagonal direction; (f) Correlation distribution of the encrypted image along the diagonal direction.
Figure 6.
Correlation analysis. (a) Correlation distribution of the plain image along the horizontal direction; (b) Correlation distribution of the encrypted image along the horizontal direction; (c) Correlation distribution of the plain image along the vertical direction; (d) Correlation distribution of the encrypted image along the vertical direction; (e) Correlation distribution of the plain image along the diagonal direction; (f) Correlation distribution of the encrypted image along the diagonal direction.
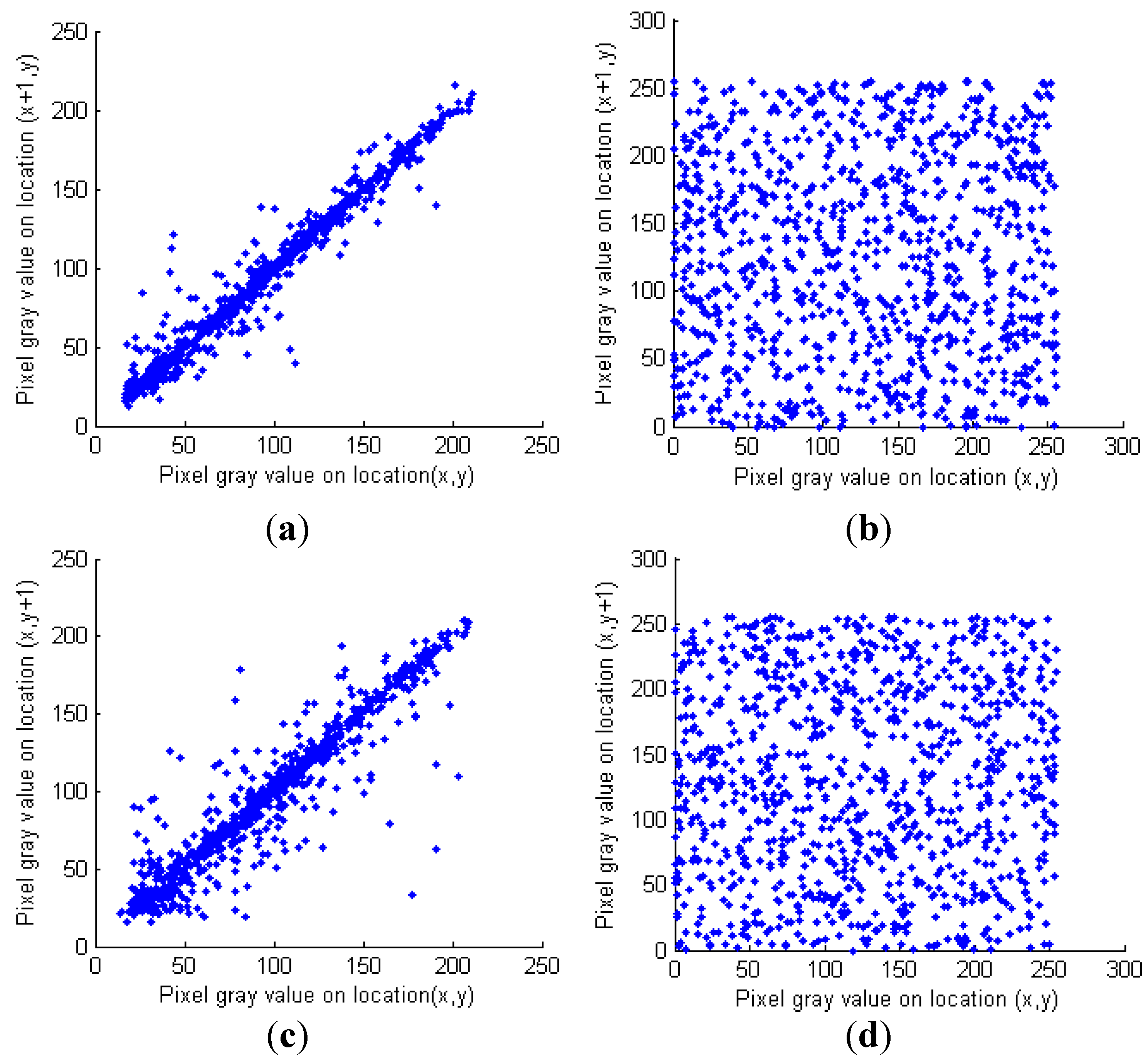
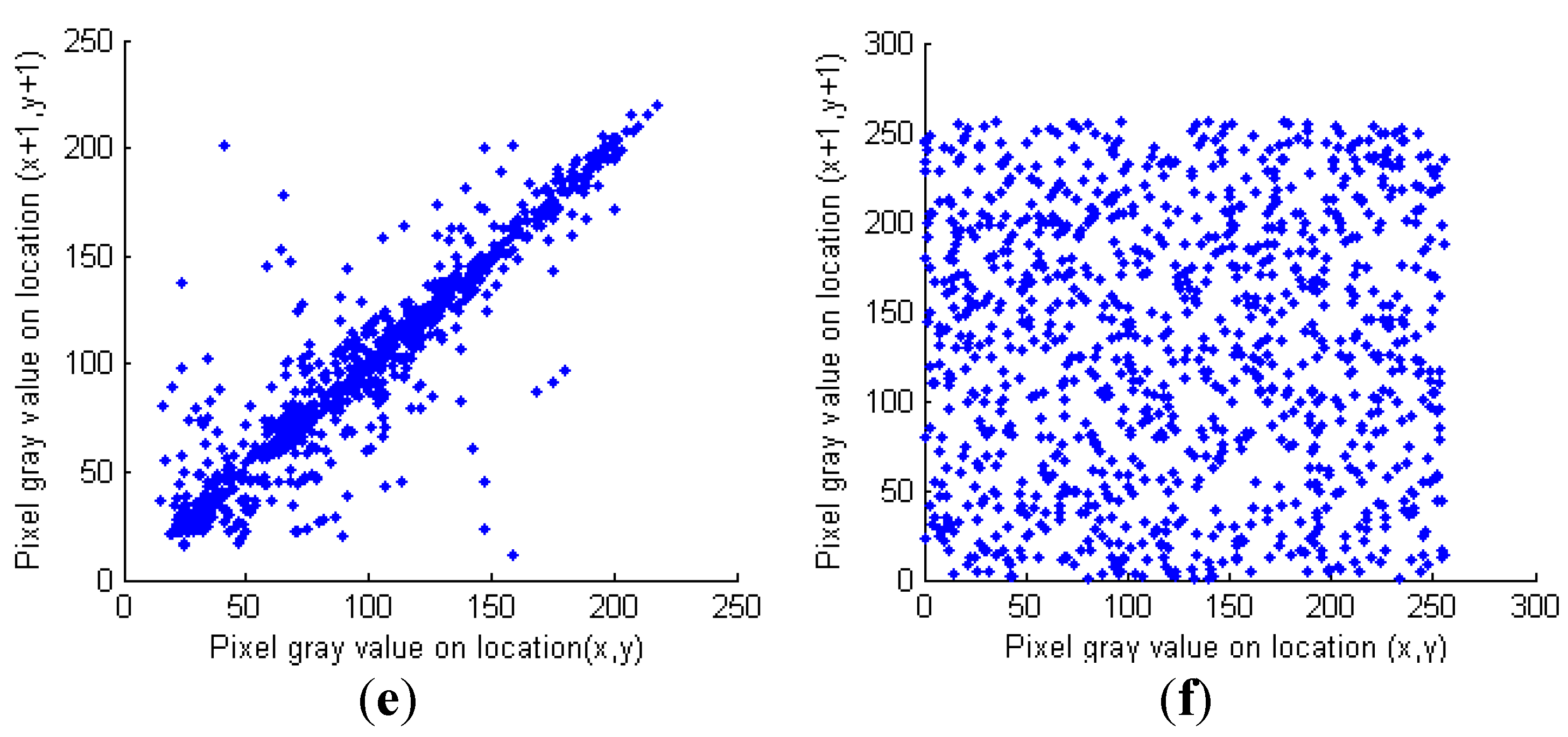

Table 3.
Correlation coefficients of two adjacent pixels.
| Horizontal | Vertical | Diagonal | ||
|---|---|---|---|---|
| Lenna | Plain image | 0.9787 | 0.9502 | 0.9332 |
| Cipher image | −0.0021 | −0.0032 | 0.0037 | |
| House | Plain image | 0.9792 | 0.9746 | 0.9602 |
| Cipher image | 0.0616 | −0.0067 | −0.0072 | |
| Couple | Plain image | 0.9402 | 0.9171 | 0.8693 |
| Cipher image | −0.0055 | 0.0317 | −0.0108 | |
| Airplane | Plain image | 0.9269 | 0.9322 | 0.8792 |
| Cipher image | 0.0169 | −0.0212 | 0.0086 | |
| Peppers | Plain image | 0.9757 | 0.9468 | 0.9133 |
| Cipher image | 0.0054 | 0.0060 | −0.0094 | |
| Camera | Plain image | 0.9547 | 0.9308 | 0.8942 |
| Cipher image | −0.0082 | −0.0012 | −0.0179 | |
| Aerial | Plain image | 0.7706 | 0.8096 | 0.6619 |
| Cipher image | −0.0223 | −0.0069 | 0.0285 | |
| Boats | Plain image | 0.9483 | 0.9263 | 0.8883 |
| Cipher image | −0.0201 | 0.0021 | 0.0046 | |

Table 4.
The comparison of the correlation coefficients of “Lenna”.
| Correlation | Horizontal | Vertical | Diagonal |
|---|---|---|---|
| Plain Lenna image | 0.9787 | 0.9502 | 0.9332 |
| Ref. [17] | 0.0023 | 0.0036 | 0.0039 |
| Ref. [15] | 0.0004 | 0.0021 | −0.0038 |
| Ref. [11] | 0.0055 | 0.0041 | 0.0002 |
| Proposed algorithm * (Figure 3b) | 0.0007 | 0.0015 | 0.0014 |
* We select the best result from several rounds.
5.4. Differential Analysis
A secure image encryption scheme must be sensitive to the plaintext. That is to say, a slight change of a pixel of the plain image can cause great change in the cipher image. For example, the gray-level at the position (115, 50) in the plain image “Lenna” is changed from 68 to 69, and the resulting cipher image C′ is shown in Figure 7a, and the differential image between the original cipher image C shown in Figure 4b and Cipher image C′ is given in Figure 7b. It can be seen that the slight change causes significant difference between the two cipher images. Such difference can be measured by means of two criteria, namely the number of pixels change rate (NPCR) and the unified average changing intensity (UACI) [25],
where W and H represent the width and height of the image, respectively. C(i, j) and C′(i, j) denote the pixel values of the ith row and jth column of images C and C′, respectively. D(i, j) is determined as follows,
In addition to the Lena image, we also test the performance of differential analysis on several benchmark images. The NPCRs and UACIs are listed in Table 5, which demonstrates the algorithm is very sensitive to the plaintext. The comparison with other algorithms is shown in Table 6.

Figure 7.
Differential analysis on “Lenna” image. (a) Cipher image C′; (b) Differential image.
Figure 7.
Differential analysis on “Lenna” image. (a) Cipher image C′; (b) Differential image.


Table 5.
The number of pixels change rate (NPCR) and unified average changing intensity (UACI) for the cipher images.
| Lenna | House | Couple | Airplane | Peppers | Camera | Aerial | Boats | |
|---|---|---|---|---|---|---|---|---|
| NPCR | 0.9958 | 0.9957 | 0.9958 | 0.9961 | 0.9956 | 0.9961 | 0.9964 | 0.9960 |
| UACI | 0.3349 | 0.3343 | 0.3347 | 0.3327 | 0.3323 | 0.3338 | 0.3342 | 0.3348 |

Table 6.
The comparison of NPCR and UACI for the cipher image of “Lenna”.
| NPCR | UACI | |
|---|---|---|
| Ref. [17] | 0.9961 | 0.3800 |
| Ref. [15] | 0.9960 | 0.2814 |
| Ref. [11] | 0.9965 | 0.3362 |
| Proposed algorithm | 0.9958 | 0.3349 |
5.5. Key Sensitivity Analysis
The key sensitivity of the algorithm is tested with the following basic expectation: (i) when a slight different key is adopted to encrypt the same image, and a completely different cipher image is obtained; (ii) the proper image cannot be decrypted when a slight difference exits between the encryption and decryption keys.
When a slightly changed key α = 1.570000000000001 is used to encrypt the plain image “Lenna”, and the cipher image is shown in Figure 8a. The differential image between Figure 8a and the original cipher image C shown in Figure 4b is given as Figure 8b, from which we can see the two cipher images are totally different.

Figure 8.
Key sensitivity analysis. (a) Cipher image (α = 1.570000000000001); (b) Differential image; (c) Decrypted image with the wrong key (ε = 0.300000000000001).
Figure 8.
Key sensitivity analysis. (a) Cipher image (α = 1.570000000000001); (b) Differential image; (c) Decrypted image with the wrong key (ε = 0.300000000000001).

The second experiment for the key sensitivity is to change the decryption key ε from 0.3 to 0.300000000000001. The corresponding decrypted image is shown in Figure 8c, from which it can be seen that the plain image cannot be decrypted with the wrong decryption key.
5.6. Key Space Analysis
From the cryptographical point of view, in order to resist the brute-force attack, the size of key space should be at least 2100 [26]. In our introduced algorithm, the key is KEY = {x0, μ, α, β, ε, L, N0}, where x0 and μ are parameters of the Logistic map, α, β, ε and L are parameters of the spatiotemporal chaotic system, N0 is to determine what part of the Logistic chaotic sequence is selected as the initial values of the spatiotemporal chaos, and K0 is the value chosen from the Logistic map to determine DNA encoding rule index IDNA and DNA decoding rule index IDDNA. According to the IEEE floating-point standard, the computational precision of the 64-bit double precision number is 10−15 [23,27], it can be estimated that the total key space at least can reach to S = 8 × x0 × μ × K0 × α × β × ε × L × N0 ≈ 1093. From Table 7, we can find that it is larger than that of Zhang’s method [17] and Song’s method [11], and smaller than that of Liu’s algorithm [15]. Therefore, the encryption scheme is secure enough to make the brute-force attack infeasible.

Table 7.
Key spaces of different algorithms.
| Algorithms | Key Space |
|---|---|
| Ref. [17] | 1072 |
| Ref. [15] | 1.92 × 10126 |
| Ref. [11] | 1065 |
| Proposed algorithm | 1093 |
6. Conclusions
This paper proposes a novel image encryption scheme based on DNA encoding and spatiotemporal chaotic system. The DNA mapping rule is introduced to encode the diffused image, and the spatiotemporal chaotic system is used to confuse the DNA encoded image. Experimental results show that the cipher image has very low neighboring pixel correlation, approximately uniform histogram distribution and can be considered as a nearly random image. The security analyses also demonstrate that the scheme is sensitive to the plain image and the encryption key, and has enough large key space. Therefore, the encryption scheme is of high security and can resist against common attacks. However, we have found from the simulation experiments that the parameter intervals of the spatiotemporal chaos may be different from that of the NCA map for ensuring the chaotic behavior. Thus, it is necessary to carry out in-depth research on the spatiotemporal chaos based NCA map. Meanwhile, we will apply the spatiotemporal chaos in other fields, such as image processing, color image encryption and chaotic map based key agreement protocol [28].
Acknowledgments
This work is partially supported by National Natural Science Foundation of China 61371175 and Fundamental Research Funds for the Central Universities HEUCFQ20150812. The authors also gratefully acknowledge the helpful comments and suggestions of the reviewers, which have improved the presentation.
Author Contributions
Both authors developed the method presented in this paper. Chunyan Song performed the experiments and data analysis, and wrote the paper. Both authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, S.; Chen, G.; Zheng, X. Chaos-based encryption for digital images and videos. In Multimedia Security Handbook; Furht, B., Kirovski, D., Eds.; CRC Press: Boca Raton, FL, USA, 2004; pp. 133–167. [Google Scholar]
- Mazloom, S.; Eftekhari-Moghadam, A.M. Color image encryption based on coupled nonlinear chaotic map. Chaos Soliton Fract. 2009, 42, 1745–1754. [Google Scholar] [CrossRef]
- Chen, W.; Chen, X. Optical image encryption based on multiple-region plaintext and phase retrieval in three-dimensional space. Opt. Laser Eng. 2013, 51, 128–133. [Google Scholar] [CrossRef]
- Chen, W.; Chen, X. Optical multiple-image authentication based on modified Gerchberg-Saxton algorithm with random sampling. Opt. Commun. 2014, 318, 128–132. [Google Scholar] [CrossRef]
- Matthews, R. On the derivation of a chaotic encryption algorithm. Cryptologia 1989, 13, 29–42. [Google Scholar] [CrossRef]
- Pareek, N.K.; Patidar, V.K.; Sud, K. Image encryption using chaotic logistic map. Image Vision Comput. 2006, 24, 926–934. [Google Scholar] [CrossRef]
- Wang, X.; Teng, L.; Qin, X. A novel colour image encryption algorithm based on chaos. Signal Process. 2012, 92, 1101–1108. [Google Scholar] [CrossRef]
- Liu, H.J.; Wang, X.Y. Color image encryption based on one-time keys and robust chaotic maps. Comput. Math. Appl. 2010, 59, 3320–3327. [Google Scholar] [CrossRef]
- Wang, X.Y.; Lei, Y.; Liu, R.; Kadir, A. A chaotic image encryption algorithm based on perceptron model. Nonlinear Dyn. 2010, 62, 615–621. [Google Scholar] [CrossRef]
- Liu, H.J.; Wang, X.Y. Color image encryption using spatial bit-level permutation and high-dimension chaotic system. Opt. Commun. 2011, 284, 3895–3903. [Google Scholar] [CrossRef]
- Song, C.Y.; Qiao, Y.L.; Zhang, X.Z. An image encryption scheme based on new spatiotemporal chaos. Optik 2013, 124, 3329–3334. [Google Scholar] [CrossRef]
- Adleman, L.M. Molecular computation of solutions to combinatorial problems. Science 1994, 266, 1021–1024. [Google Scholar] [CrossRef] [PubMed]
- Xiao, G.; Lu, M.; Qin, L.; Lai, X. New field of cryptography: DNA cryptography. Chin. Sci. Bull. 2006, 51, 1413–1420. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, L.H.B. Research on DNA cryptography. In Applied Cryptography and Network Security; Sen, J., Ed.; InTech: Rijeka, Croatia, 2012. [Google Scholar]
- Liu, H.; Wang, X.; Kadir, A. Image encryption using DNA complementary rule and chaotic maps. Appl. Soft Comput. 2012, 12, 1457–1466. [Google Scholar] [CrossRef]
- Gehani, A.; LaBean, T.H.; Reif, J.H. DNA-Based Cryptography. In DIMACS Series in Discrete Mathematics and Theoretical Computer Science, Proceedings of the 5th DIMACS Workshop on DNA Based Computers V, MIT, Cambridge, MA, USA; Winfree, E., Gifford, D.K., Eds.; 1999; Volume 54, pp. 233–249. [Google Scholar]
- Zhang, Q.; Guo, L.; Wei, X.P. Image encryption using DNA addition combining with chaotic maps. Math. Comput. Model. 2010, 52, 2028–2035. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Y.; Liang, S.; Li, D. A new chaotic algorithm for image encryption. Chaos Soliton Fract. 2006, 29, 393–399. [Google Scholar] [CrossRef]
- Wang, X.Y.; Wang, M.J. A hyperchaos generated from Lorenz system. Physica A 2008, 387, 3751–3758. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Wang, X.Y. A symmetric image encryption algorithm based on mixed linear-nonlinear coupled map lattice. Inf. Sci. 2014, 273, 329–351. [Google Scholar] [CrossRef]
- Behnia, S.; Akhshani, A.; Ahadpour, S.; Mahmodi, H.; Akhavan, A. A fast chaotic encryption scheme based on piecewise nonlinear chaotic maps. Phys. Lett. A 2007, 366, 391–396. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Fu, C.; Lin, B.; Miao, Y.; Liu, X.; Chen, J. A novel chaos-based bit-level permutation scheme for digital image encryption. Opt. Commun. 2011, 284, 5415–5423. [Google Scholar] [CrossRef]
- Ye, R. A novel chaos-based image encryption scheme with an efficient permutation-diffusion mechanism. Opt. Commun. 2011, 284, 5290–5298. [Google Scholar] [CrossRef]
- Akhavan, A.; Samsudin, A.; Akhshani, A. A symmetric image encryption scheme based on combination of nonlinear chaotic maps. J. Franklin Inst. 2011, 348, 1797–1813. [Google Scholar] [CrossRef]
- Alvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based cryptosystems. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar]
- IEEE Computer Society. IEEE Standard for Binary Floating-Point Arithmetic. Available online: http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=30711 (accessed on 14 October 2015).
- Niu, Y.; Wang, X. An anonymous key agreement protocol based on chaotic maps. Commun. Nonlinear Sci. 2011, 16, 1986–1992. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
