Reentrant Phase Transitions and van der Waals Behaviour for Hairy Black Holes
Abstract
:1. Introduction
2. Solution & Thermodynamics
3. Critical Behaviour
3.1. Spherical
3.1.1. Uncharged Case


3.1.2. Charged Case
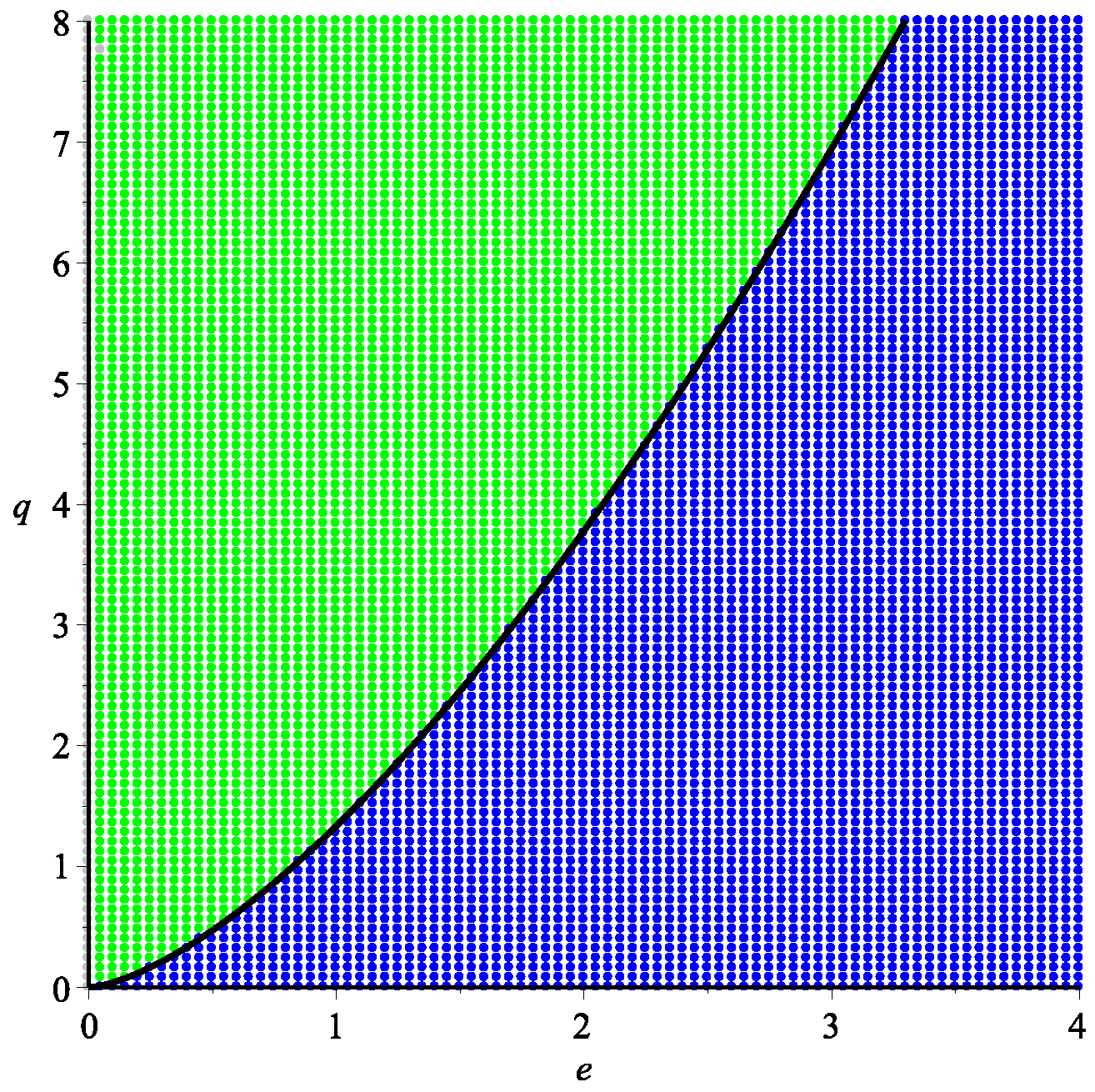

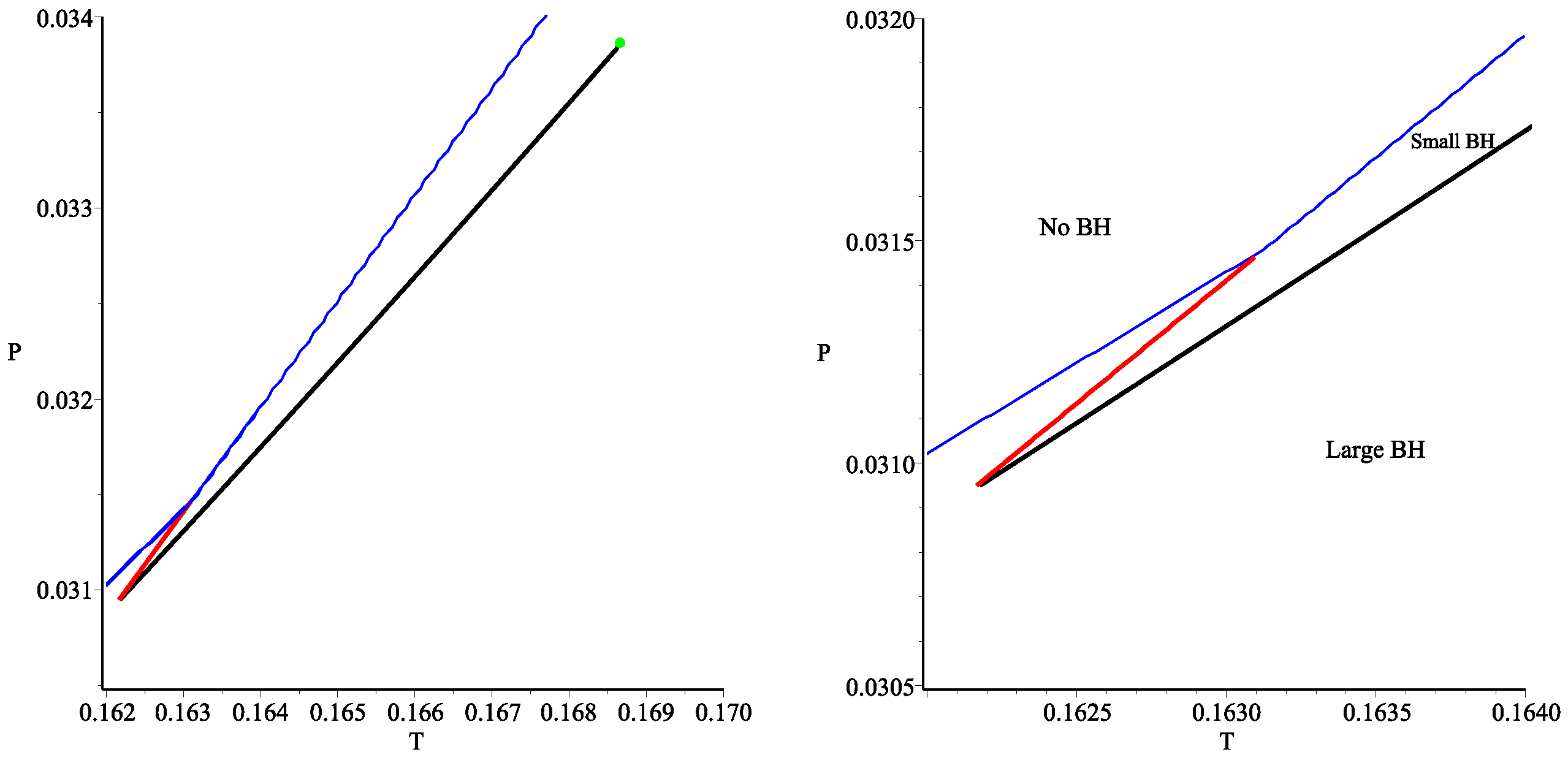
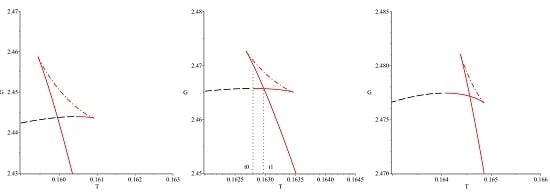
3.2. Hyperbolic
3.3. Black Holes with Zero Entropy
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix: Black Holes with Zero or Negative Mass
References
- Creighton, J.; Mann, R. Quasilocal thermodynamics of dilaton gravity coupled to gauge fields. Phys. Rev. D 1995, 52, 4569–4587. [Google Scholar] [CrossRef]
- Caldarelli, M.M.; Cognola, G.; Klemm, D. Thermodynamics of Kerr-Newman-AdS black holes and conformal field theories. Class. Quantum Gravity 2000, 17, 399–420. [Google Scholar] [CrossRef]
- Dolan, B.P. The cosmological constant and the black hole equation of state. Class. Quantum Gravity 2011, 28, 125020. [Google Scholar] [CrossRef]
- Dolan, B.P. Pressure and volume in the first law of black hole thermodynamics. Class. Quantum Gravity 2011, 28, 235017. [Google Scholar] [CrossRef]
- Dolan, B.P. Black holes and Boyle’s law—The thermodynamics of the cosmological constant. Mod. Phys. Lett. A 2014. [Google Scholar] [CrossRef]
- Kastor, D.; Ray, S.; Traschen, J. Enthalpy and the Mechanics of AdS Black Holes. Class. Quantum Gravity 2009, 26, 195011. [Google Scholar] [CrossRef]
- Kubiznak, D.; Mann, R.B. Black Hole Chemistry; Gravity Research Foundation: Wellesley Hills, MA, USA, 2014. [Google Scholar]
- Kubiznak, D.; Mann, R.B. P − V criticality of charged AdS black holes. J. High Energy Phys. 2012, 2012, 1–25. [Google Scholar] [CrossRef]
- Altamirano, N.; Kubiznak, D.; Mann, R.B.; Sherkatghanad, Z. Kerr-AdS analogue of triple point and solid/liquid/gas phase transition. Class. Quantum Gravity 2014, 31, 042001. [Google Scholar] [CrossRef]
- Altamirano, N.; Kubiznak, D.; Mann, R.B. Reentrant phase transitions in rotating anti–de Sitter black holes. Phys. Rev. D 2013, 88, 101502. [Google Scholar] [CrossRef]
- Altamirano, N.; Kubiznak, D.; Mann, R.B.; Sherkatghanad, Z. Thermodynamics of rotating black holes and black rings: Phase transitions and thermodynamic volume. Galaxies 2014, 2, 89–159. [Google Scholar] [CrossRef]
- Frassino, A.M.; Kubiznak, D.; Mann, R.B.; Simovic, F. Multiple Reentrant Phase Transitions and Triple Points in Lovelock Thermodynamics. J. High Energy Phys. 2014, 2014, 1–47. [Google Scholar] [CrossRef]
- Hennigar, R.A.; Brenna, W.G.; Mann, R.B. P–V criticality in quasitopological gravity. J. High Energy Phys. 2015. [Google Scholar] [CrossRef]
- Dolan, B.P.; Kostouki, A.; Kubiznak, D.; Mann, R.B. Isolated critical point from Lovelock gravity. Class. Quantum Gravity 2014, 31, 242001. [Google Scholar] [CrossRef]
- Gunasekaran, S.; Mann, R.B.; Kubiznak, D. Extended phase space thermodynamics for charged and rotating black holes and Born-Infeld vacuum polarization. J. High Energy Phys. 2012. [Google Scholar] [CrossRef]
- Cai, R.-G.; Cao, L.-M.; Li, L.; Yang, R.-Q. P-V criticality in the extended phase space of Gauss-Bonnet black holes in AdS space. J. High Energy Phys. 2013. [Google Scholar] [CrossRef]
- Hendi, S.H.; Vahidinia, M.H. Extended phase space thermodynamics and P-V criticality of black holes with a nonlinear source. Phys. Rev. D 2013, 88, 084045. [Google Scholar] [CrossRef]
- Mo, J.-X.; Liu, W.-B. Ehrenfest scheme for P − V criticality of higher dimensional charged black holes, rotating black holes and Gauss-Bonnet AdS black holes. Phys. Rev. D 2014, 89, 084057. [Google Scholar] [CrossRef]
- Rajagopal, A.; Kubiznak, D.; Mann, R.B. Van der Waals black hole. Phys. Lett. 2014, B737, 277–279. [Google Scholar] [CrossRef]
- Delsate, T.; Mann, R. Van Der Waals Black Holes in d dimensions. J. High Energy Phys. 2015. [Google Scholar] [CrossRef]
- Setare, M.; Adami, H. Polytropic black hole. Phys. Rev. D 2015, 91, 084014. [Google Scholar] [CrossRef]
- Cvetic, M.; Gibbons, G.; Kubiznak, D.; Pope, C. Black Hole Enthalpy and an Entropy Inequality for the Thermodynamic Volume. Phys. Rev. D 2011, 84, 024037. [Google Scholar] [CrossRef]
- Hennigar, R.A.; Kubiznak, D.; Mann, R.B. Entropy Inequality Violations from Ultraspinning Black Holes. Phys. Rev. Lett. 2015, 115, 031101. [Google Scholar] [CrossRef] [PubMed]
- Johnson, C.V. Holographic Heat Engines. Class. Quantum Gravity 2014, 31, 205002. [Google Scholar] [CrossRef]
- Caceres, E.; Nguyen, P.H.; Pedraza, J.F. Holographic entanglement entropy and the extended phase structure of STU black holes. JHEP 2015. arXiv:1507.06069. [Google Scholar] [CrossRef]
- Martinez, C.; Zanelli, J. Conformally dressed black hole in (2 + 1)-dimensions. Phys. Rev. D 2011, 54, 3830–3833. [Google Scholar] [CrossRef]
- Hartnoll, S.A.; Herzog, C.P.; Horowitz, G.T. Building a Holographic Superconductor. Phys. Rev. Lett. 2008, 101, 031601. [Google Scholar] [CrossRef] [PubMed]
- Gubser, S.S. Breaking an Abelian gauge symmetry near a black hole horizon. Phys. Rev. D 2008, 78, 065034. [Google Scholar] [CrossRef]
- Oliva, J.; Ray, S. Conformal couplings of a scalar field to higher curvature terms. Class. Quantum Gravity 2012, 29, 205008. [Google Scholar] [CrossRef]
- Galante, M.; Giribet, G.; Goya, A.; Oliva, J. Chemical potential driven phase transition of black holes in AdS space. Available online: http://arxiv.org/abs/1508.03780 (accessed on 7 December 2015).
- Giribet, G.; Leoni, M.; Oliva, J.; Ray, S. Hairy black holes sourced by a conformally coupled scalar field in D dimensions. Phys. Rev. D 2014, 89, 085040. [Google Scholar] [CrossRef]
- Giribet, G.; Goya, A.; Oliva, J. Different phases of hairy black holes in AdS5 space. Phys. Rev. D 2015, 91, 045031. [Google Scholar] [CrossRef]
- Wald, R.M. Black hole entropy is the Noether charge. Phys. Rev. D 1993, 48, 3427–3431. [Google Scholar] [CrossRef]
- Wei, S.-W.; Liu, Y.-X. Clapeyron equations and fitting formula of the coexistence curve in the extended phase space of charged AdS black holes. Phys. Rev. 2015, D91, 044018. [Google Scholar] [CrossRef]
- Hudson, C. The mutual solubility of nicotine in water. Zeit. Phys. Chem. 1904, 47, 113. [Google Scholar]
- Mann, R.B. Topological black holes: Outside looking in. Available online: http://arxiv.org/abs/gr-qc/9709039 (accessed on 7 December 2015).
- Smith, W.L.; Mann, R.B. Formation of topological black holes from gravitational collapse. Phys. Rev. D 1997, 56, 4942–4947. [Google Scholar] [CrossRef]
- Mann, R.B. Black holes of negative mass. Class. Quantum Gravity 1997, 14, 2927–2930. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hennigar, R.A.; Mann, R.B. Reentrant Phase Transitions and van der Waals Behaviour for Hairy Black Holes. Entropy 2015, 17, 8056-8072. https://doi.org/10.3390/e17127862
Hennigar RA, Mann RB. Reentrant Phase Transitions and van der Waals Behaviour for Hairy Black Holes. Entropy. 2015; 17(12):8056-8072. https://doi.org/10.3390/e17127862
Chicago/Turabian StyleHennigar, Robie A., and Robert B. Mann. 2015. "Reentrant Phase Transitions and van der Waals Behaviour for Hairy Black Holes" Entropy 17, no. 12: 8056-8072. https://doi.org/10.3390/e17127862
APA StyleHennigar, R. A., & Mann, R. B. (2015). Reentrant Phase Transitions and van der Waals Behaviour for Hairy Black Holes. Entropy, 17(12), 8056-8072. https://doi.org/10.3390/e17127862