Statistical Correlations of the N-particle Moshinsky Model
Abstract
:1. Introduction
2. Moshinsky Model
3. Shannon Entropy and Testing Entropic Uncertainty Principle
3.1. Position Space
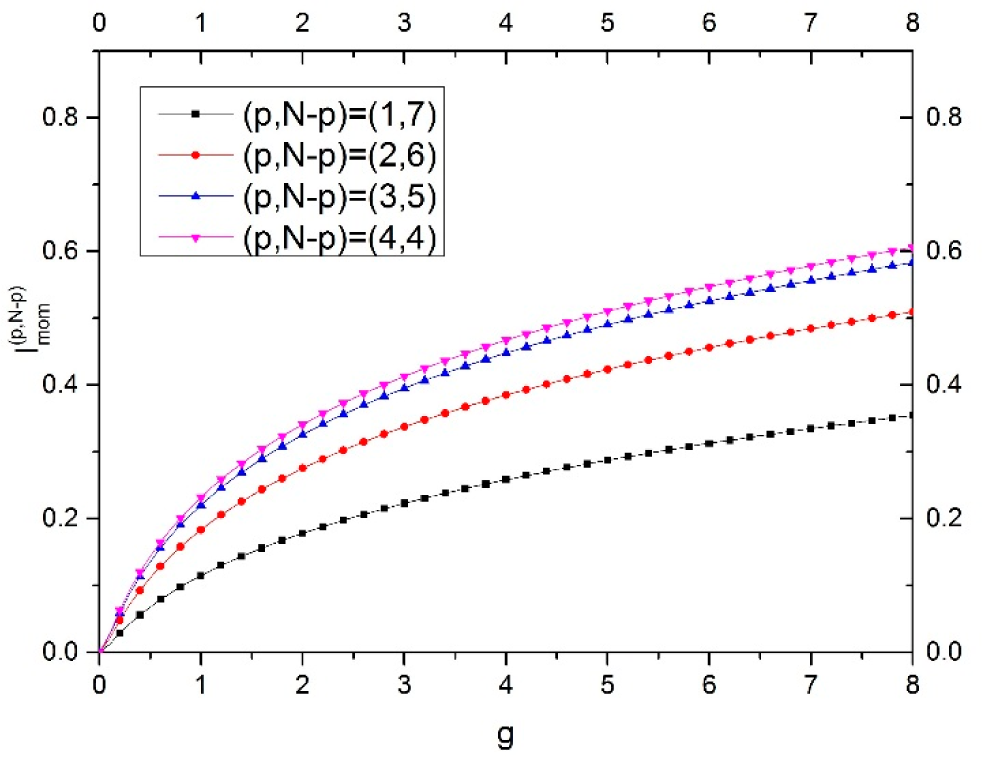
3.2. Momentum Space
3.3. Relation of Two Spaces and Testing Entropic Uncertainty Principle
3.4. Comparing Statistical Correlation to Quantum Correlation
4. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Moshinsky, H.M. How good is the Hartree-Fock approximation. Am. J. Phys. 1968, 36, 52–53. [Google Scholar]
- Laguna, H.G.; Sagar, R.P. Statistical correlations in the Moshinsky atom. Phys. Rev. A 2011, 84, 012502. [Google Scholar]
- Yanez, R.J.; Plastino, A.R.; Dehesa, J.S. Quantum entanglement in a soluble two-electron model atom. Eur. Phys. J. D 2010, 56, 141–150. [Google Scholar]
- Manzano, D.; Plastino, A.R.; Dehesa, J.S.; Koga, T. Quantum entanglement in two-electron atomic models. J. Phys. A Math. Theor. 2010, 43, 275301. [Google Scholar]
- Bouvrie, P.A.; Majtey, A.P.; Plastino, A.R.; Sanchez-Moreno, P.; Dehesa, J.S. Quantum entanglement in exactly soluble atomic models: the Moshinsky model with three electrons, and with two electrons in a uniform magnetic field. Eur. Phys. J. D 2012, 66. [Google Scholar] [CrossRef]
- Kościk, P.; Okopińska, A. Correlation effects in the Moshinsky model. Few-Body Syst 2013, 54, 1637–1640. [Google Scholar]
- Laguna, H.G.; Sagar, R.P. Indistinguishability and correlation in model systems. J. Phys. A Math. Theor. 2011, 44, 185302. [Google Scholar]
- Laguna, H.G.; Sagar, R.P. Phase-space position-momentum correlation and potentials. Entropy 2013, 15, 1516–1527. [Google Scholar]
- Laguna, H.G.; Sagar, R.P. Position–momentum correlations in the Moshinsky atom. J. Phys. A Math. Theor. 2012, 45, 025307. [Google Scholar]
- Laguna, H.G.; Sagar, R.P. Wave function symmetry, symmetry holes, interaction and statistical correlation in the Moshinsky atom. Physica A 2014, 396, 267–279. [Google Scholar]
- Guevara, N.L.; Sagar, R.P.; Esquivel, R.O. Shannon-information entropy sum as a correlation measure in atomic systems. Phys. Rev. A 2003, 67, 012507. [Google Scholar]
- Shi, Q.; Kais, S. Finite Size Scaling for the atomic Shannon-information entropy. J. Chem. Phys. 2004, 121, 5611–5617. [Google Scholar]
- Sen, K.D. Characteristic features of Shannon information entropy of confined atoms. J. Chem. Phys. 2005, 123, 074110. [Google Scholar]
- Chatzisavvas, K.C.; Moustakidis, C.C.; Panos, C.P. Information entropy, information distances, and complexity in atoms. J. Chem. Phys. 2005, 123, 174111. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley: Hoboken, NJ, USA, 1991; pp. 12–49. [Google Scholar]
- Sagar, R.P.; Guevara, N.L. Mutual information and correlation measures in atomic systems. J. Chem. Phys. 2005, 123, 044108. [Google Scholar]
- Sagar, R.P.; Guevara, N.L. Mutual information and electron correlation in momentum space. J. Chem. Phys. 2006, 124, 134101. [Google Scholar]
- Sagar, R.P.; Laguna, H.G.; Guevara, N.L. Conditional entropies and position-momentum correlations in atomic systems. Mol. Phys. 2009, 107, 2071–2080. [Google Scholar]
- Bialynicki-Birula, I.; Mycielski, J. Uncertainty relations for information entropy in wave mechanics. Commun. Math. Phys. 1975, 44, 129–132. [Google Scholar]
- Guevara, N.L.; Sagar, R.P.; Esquivel, R.O. Information uncertainty-type inequalities in atomic systems. J. Chem. Phys. 2003, 119, 7030–7036. [Google Scholar]
- Lin, C.H.; Ho, Y.K. Quantification of entanglement entropy in helium by the Schmidt–Slater decomposition method. Few-Body Syst. 2014, 55, 1141–1149. [Google Scholar]
- Lin, C.H.; Ho, Y.K. Calculation of von Neumann entropy for hydrogen and positronium negative ions. Phys. Lett. A 2014, 378, 2861–2865. [Google Scholar]
- Lin, C.H.; Lin, Y.C.; Ho, Y.K. Quantification of linear entropy for quantum entanglement in He, H− and Ps− ions using highly-correlated Hylleraas functions. Few-Body Syst. 2013, 54, 2147–2153. [Google Scholar]
- Lin, Y.C.; Ho, Y.K. Quantum entanglement for two electrons in the excited states of helium-like systems. Can. J. Phys. 2015. [Google Scholar] [CrossRef]
- Lin, Y.C.; Lin, C.Y.; Ho, Y.K. Spatial entanglement in two-electron atomic systems. Phys. Rev. A 2013, 87, 022316. [Google Scholar]
- Majtey, A.P.; Plastino, A.R.; Dehesa, J.S. The relationship between entanglement, energy and level degeneracy in two-electron systems. J. Phys. A Math. Theor. 2012, 45, 115309. [Google Scholar]
- Jaeger, G. Quantum Information—An Overview, 1st ed.; Springer: New York, NY, USA, 2006; Chapter 5; pp. 85–86. [Google Scholar]
- Pruski, S.; Mać kowiak, J.; Missuno, O. Reduced density matrices of a system of N coupled oscillators 3. Eigenstructure of the p-particle matric for the ground-state. Rep. Math. Phys. 1972, 3, 241–246. [Google Scholar]







© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, H.T.; Ho, Y.K. Statistical Correlations of the N-particle Moshinsky Model. Entropy 2015, 17, 1882-1895. https://doi.org/10.3390/e17041882
Peng HT, Ho YK. Statistical Correlations of the N-particle Moshinsky Model. Entropy. 2015; 17(4):1882-1895. https://doi.org/10.3390/e17041882
Chicago/Turabian StylePeng, Hsuan Tung, and Yew Kam Ho. 2015. "Statistical Correlations of the N-particle Moshinsky Model" Entropy 17, no. 4: 1882-1895. https://doi.org/10.3390/e17041882




