Energetic and Exergetic Analysis of an Ejector-Expansion Refrigeration Cycle Using the Working Fluid R32
Abstract
:1. Introduction
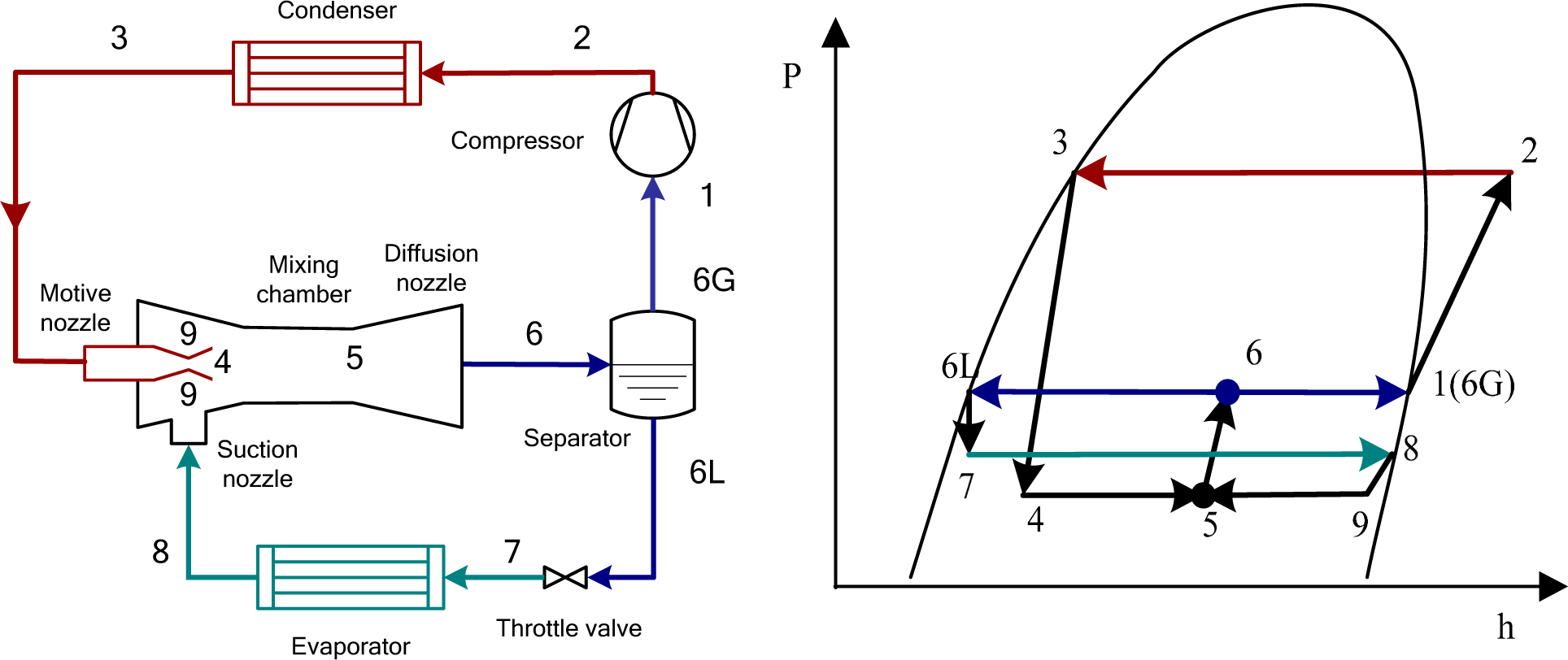
2. Cycle Description
3. Thermodynamic analysis
- One dimensional steady flow for the working fluid in the system.
- Saturated vapor and liquid at the outlet of the gas-liquid separator.
- Mixing occurs at a constant pressure, less than the inlet pressure of the suction flow.
- Expansion processes and compression processes are all adiabatic. The ejector geometry effects are assumed to be considered in terms of isentropic efficiencies of the ejector components.
- The separator offered zero pressure drop and had 100% effectiveness in separating the two-phase mixture into saturated vapor and liquid [13].
3.1. Energy Analysis
3.2. Exergy Analysis
- The property parameters at states 8 and 3 are calculated based on the given condensing temperature, evaporating temperature, subcooling and superheat.
- The property parameters at states 9 and 4 are calculated by given ηmn, ηsn, and SNPD. Fluid velocities at the corresponding states are calculated by Equations (5) and (8).
- Some value of μ is presumed.
- The property parameters and fluid velocity at state 5 are calculated by Equations (10) and (11).
- Enthalpy, pressure, vapor quality and other property parameters at state 6 are calculated by given ηdn and Equations (12)–(14).
- Steps (iii)–(v) are iterated until Equation (15) is satisfied.
- The other performance parameters are calculated by the other equations.
4. Results and Discussion
5. Conclusions
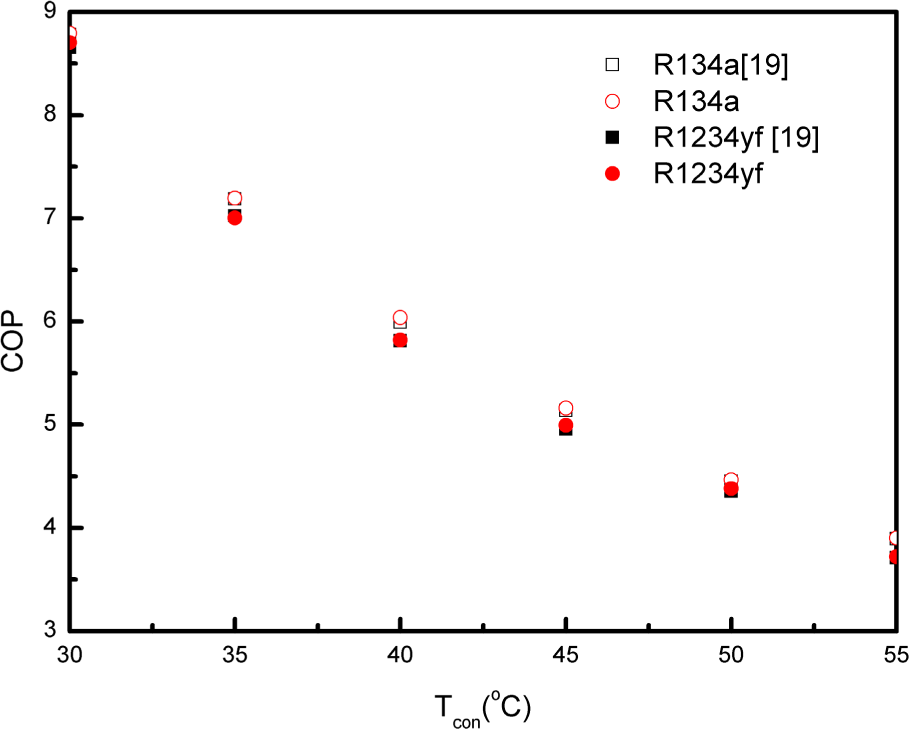
- The cycle COP of R32 and R134a EEC are at a range of 3.578–8.464 and 3.749–8.792, respectively. The R32 EEC and the R134a EEC have a 5.22%–13.77% and 6.63%–17.83% improvement in COP over the corresponding basic cycle, respectively.
- The application of an ejector instead of a throttle valve decreases the cycle’s total exergy destruction by 8.84%–15.84% and 10.16%–19.38% for R32 and R134a, respectively.
- The exergy efficiency of the R32 and R134a EEC varies from 0.2189 to 0.5081 and from 0.2346 to 0.5284, respectively. The application of an ejector instead of a throttle valve yields 5.13%–13.83% and 6.68–17.95% improvement in exergy efficiency over the corresponding basic cycle respectively for R32 and R134a.
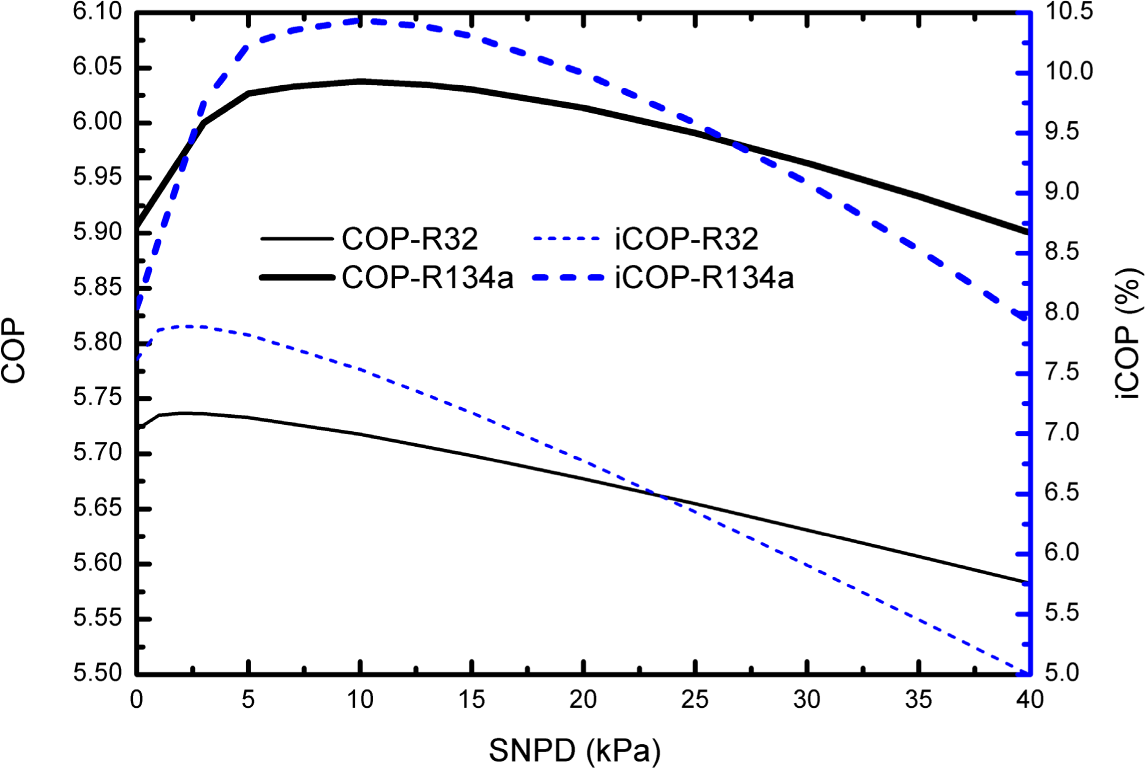
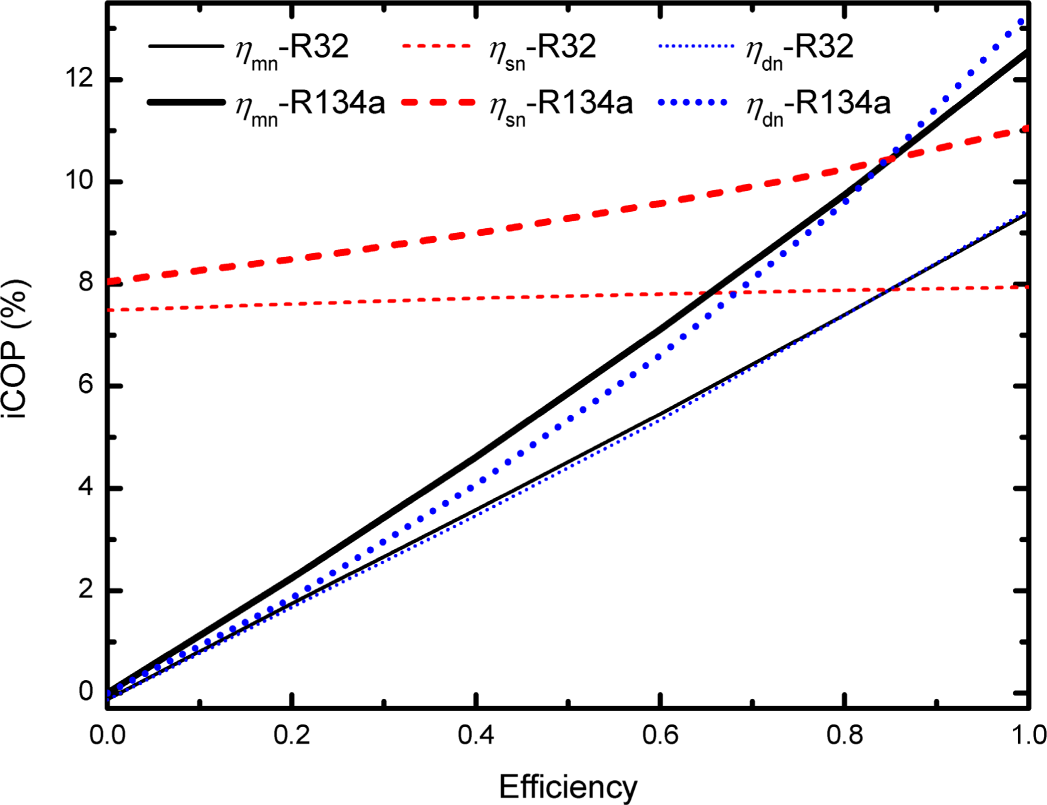
- There exists an optimum SNPD which gives a maximum system COP and VCC under a specified condition. The value of the optimum SNPD mainly depends on the efficiencies of the ejector components, but is virtually independent of evaporating temperature and condensing temperature. The optimum SNPD varies from 0 to 3 kPa and from 0 to 17 kPa for R32 and R134a respectively. Among the components of ejector, the effect of the diffusion nozzle efficiency on the optimum SNPD is relatively more significant. In addition, the improvement of the component efficiency, especially the efficiencies of diffusion nozzle and the motive nozzle, can enhance the EEC performance.
Nomenclature
| BC | basic refrigeration cycle |
| COP | coefficient of performance |
| CPR | compression pressure ratio |
| EEC | ejector-expansion refrigeration cycle |
| Ex | exergy [kJ/kg] |
| h | enthalpy [kJ/kg] |
| iCOP | improvement of COP |
| iEx | variation ratio of exergy destruction |
| iVCC | improvement of volumetric cooling capacity |
| m | mass flow rate [kg/s] |
| p | pressure [kPa] |
| PLR | pressure lift ratio |
| q | specific heat transfer rate [kJ/kg] |
| s | specific entropy [kJ/(kg.K)] |
| SNPD | suction nozzle pressure drop [kPa] |
| t | temperature [°C] |
| T | temperature [K] |
| v | velocity [m/s] |
| VCC | volumetric cooling capacity [kJ/m3] |
| w | specific power [kJ/kg] |
| x | vapor quality |
| η | efficiency |
| μ | entrainment ratio of ejector |
| Subscripts | |
|---|---|
| 0 | reference environment |
| com | compressor |
| con | condenser |
| dn | diffusion nozzle |
| eva | evaporator |
| mix | mixing chamber |
| hx | heat exchanger |
| mn | motive nozzle |
| r | refrigerated object |
| sn | suction nozzle |
| tot | totle |
| tv | throttle valve |
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Elbel, S. Historical and present developments of ejector refrigeration systems with emphasis on transcritical carbon dioxide air-conditioning applications. Int. J. Refrig. 2011, 34, 1545–1561. [Google Scholar]
- Ahammed, M.E.; Bhattacharyya, S.; Ramgopal, M. Thermodynamic design and simulation of a CO2 based transcritical vapour compression refrigeration system with an ejector. Int. J. Refrig. 2014, 45, 177–188. [Google Scholar]
- Goodarzi, M.; Gheibi, A.; Motamedian, M. Comparative analysis of an improved two-stage multi-inter-cooling ejector-expansion trans-critical CO2 refrigeration cycle. Appl. Therm. Eng. 2015, 81, 58–65. [Google Scholar]
- Lee, J.S.; Kim, M.S.; Kim, M.S. Studies on the performance of a CO2 air conditioning system using an ejector as an expansion device. Int. J. Refrig. 2014, 38, 140–152. [Google Scholar]
- Li, D.; Groll, E.A. Transcritical CO2 refrigeration cycle with ejector-expansion device. Int. J. Refrig. 2005, 28, 766–773. [Google Scholar]
- Liu, F.; Groll, E.A.; Li, D. Investigation on performance of variable geometry ejectors for CO2 refrigeration cycles. Energy 2012, 45, 829–839. [Google Scholar]
- Nakagawa, M.; Marasigan, A.R.; Matsukawa, T.; Kurashina, A. Experimental investigation on the effect of mixing length on the performance of two-phase ejector for CO2 refrigeration cycle with and without heat exchanger. Int. J. Refrig. 2011, 34, 1604–1613. [Google Scholar]
- Zhang, Z.-Y.; Ma, Y.-T.; Wang, H.-L.; Li, M.-X. Theoretical evaluation on effect of internal heat exchanger in ejector expansion transcritical CO2 refrigeration cycle. Appl. Therm. Eng. 2013, 50, 932–938. [Google Scholar]
- Sumeru, K.; Nasution, H.; Ani, F.N. A review on two-phase ejector as an expansion device in vapor compression refrigeration cycle. Renew. Sustain. Energy Rev. 2012, 16, 4927–4937. [Google Scholar]
- Manjili, F.E.; Yavari, M.A. Performance of a new two-stage multi-intercooling transcritical CO2 ejector refrigeration cycle. Appl. Therm. Eng. 2012, 40, 202–209. [Google Scholar]
- Banasiak, K.; Palacz, M.; Hafner, A.; Buliński, Z.; Smołka, J.; Nowak, A.J.; Fic, A. A CFD-based investigation of the energy performance of two-phase R744 ejectors to recover the expansion work in refrigeration systems: An irreversibility analysis. Int. J. Refrig. 2014, 40, 328–337. [Google Scholar]
- Kornhauser, A.A. The use of an ejector as a refrigerant expander. Proceedings of the 1990 USNC/IIR-Purdue Refrigeration Conference, West Lafayette, IN, USA, 14–17 July 1990; pp. 10–19.
- Domanski, P.A. Theoretical Evaluation of the Vapor Compression Cycle with a Liquid-Line/Suction-Line Heat Exchanger, Economizer, and Ejector; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1995. [Google Scholar]
- Nehdi, E.; Kairouani, L.; Bouzaina, M. Performance analysis of the vapour compression cycle using ejector as an expander. Int. J. Energy Res. 2007, 31, 364–375. [Google Scholar]
- Bilir, N.; Ersoy, H.K. Performance improvement of the vapour compression refrigeration cycle by a two-phase constant area ejector. Int. J. Energy Res. 2009, 33, 469–480. [Google Scholar]
- Disawas, S.; Wongwises, S. Experimental investigation on the performance of the refrigeration cycle using a two-phase ejector as an expansion device. Int. J. Refrig. 2004, 27, 587–594. [Google Scholar]
- Wongwises, S.; Disawas, S. Performance of the two-phase ejector expansion refrigeration cycle. Int. J. Heat Mass Transf. 2005, 48, 4282–4286. [Google Scholar]
- Pottker, G.; Hrnjak, P. Ejector in R410A vapor compression systems with experimental quantification of two major mechanisms of performance improvement: Work recovery and liquid feeding. Int. J. Refrig. 2015, 50, 184–192. [Google Scholar]
- Li, H.; Cao, F.; Bu, X.; Wang, L.; Wang, X. Performance characteristics of R1234yf ejector-expansion refrigeration cycle. Appl. Energy. 2014, 121, 96–103. [Google Scholar]
- Bilir Sag, N.; Ersoy, H.K.; Hepbasli, A.; Halkaci, H.S. Energetic and exergetic comparison of basic and ejector expander refrigeration systems operating under the same external conditions and cooling capacities. Energy Convers. Manag. 2015, 90, 184–194. [Google Scholar]
- Lawrence, N.; Elbel, S. Experimental investigation of a two-phase ejector cycle suitable for use with low-pressure refrigerants R134a and R1234yf. Int. J. Refrig. 2014, 38, 310–322. [Google Scholar]
- Brunin, O.; Feidt, M.; Hivet, B. Comparison of the working domains of some compression heat pumps and a compression-absorption heat pump. Int. J. Refrig. 1997, 20, 308–318. [Google Scholar]
- Lemmon, E.; Huber, M.; McLinden, M. NIST Reference Fluid Thermodynamic and Transport Properties—REFPROP, Version 8.0; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2007. [Google Scholar]
- Sarkar, J. Performance characteristics of natural-refrigerants-based ejector expansion refrigeration cycles. Proc. Inst. Mech. Eng. A 2009, 223, 543–550. [Google Scholar]
- Ersoy, H.K.; Bilir, N. Performance characteristics of ejector expander transcritical CO2 refrigeration cycle. Proc. Inst. Mech. Eng. A 2012, 226, 623–635. [Google Scholar]
- Zhang, Z.; Tian, L. Effect of suction nozzle pressure drop on the performance of an ejector-expansion transcritical CO2 refrigeration cycle. Entropy 2014, 16, 4309–4321. [Google Scholar]











| Process | R32
| R134a
| ||||||
|---|---|---|---|---|---|---|---|---|
| BC
| EEC
| BC
| EEC
| |||||
| Ex (kJ/kg) | (%) | Ex (kJ/kg) | (%) | Ex (kJ/kg) | (%) | Ex (kJ/kg) | (%) | |
| Compression | 6.398 | 20.78 | 5.894 | 21.41 | 4.126 | 23.15 | 3.705 | 23.97 |
| Condensing | 14.05 | 45.63 | 13.67 | 49.65 | 7.316 | 41.05 | 7.262 | 46.99 |
| Ejector | – | – | 3.438 | 12.49 | – | – | 1.769 | 11.45 |
| Throttling | 5.899 | 19.16 | 0.08396 | 0.31 | 3.712 | 20.83 | 0.02212 | 0.14 |
| Evaporation | 4.443 | 14.43 | 4.447 | 16.15 | 2.670 | 14.98 | 2.697 | 17.45 |
| Total | 30.79 | 100 | 27.53 | 100 | 17.82 | 100 | 15.46 | 100 |
| ηex | 0.3194 | 0.344 | 0.3284 | 0.3631 | ||||
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Tong, L.; Chang, L.; Chen, Y.; Wang, X. Energetic and Exergetic Analysis of an Ejector-Expansion Refrigeration Cycle Using the Working Fluid R32. Entropy 2015, 17, 4744-4761. https://doi.org/10.3390/e17074744
Zhang Z, Tong L, Chang L, Chen Y, Wang X. Energetic and Exergetic Analysis of an Ejector-Expansion Refrigeration Cycle Using the Working Fluid R32. Entropy. 2015; 17(7):4744-4761. https://doi.org/10.3390/e17074744
Chicago/Turabian StyleZhang, Zhenying, Lirui Tong, Li Chang, Yanhua Chen, and Xingguo Wang. 2015. "Energetic and Exergetic Analysis of an Ejector-Expansion Refrigeration Cycle Using the Working Fluid R32" Entropy 17, no. 7: 4744-4761. https://doi.org/10.3390/e17074744
APA StyleZhang, Z., Tong, L., Chang, L., Chen, Y., & Wang, X. (2015). Energetic and Exergetic Analysis of an Ejector-Expansion Refrigeration Cycle Using the Working Fluid R32. Entropy, 17(7), 4744-4761. https://doi.org/10.3390/e17074744





