Friction Signal Denoising Using Complete Ensemble EMD with Adaptive Noise and Mutual Information

Abstract

During the measurement of friction force, the measured signal generally contains noise. To remove the noise and preserve the important features of the signal, a hybrid filtering method is introduced that uses the mutual information and a new waveform. This new waveform is the difference between the original signal and the sum of intrinsic mode functions (IMFs), which are obtained by empirical mode decomposition (EMD) or its improved versions. To evaluate the filter performance for the friction signal, ensemble EMD (EEMD), complementary ensemble EMD (CEEMD), and complete ensemble EMD with adaptive noise (CEEMDAN) are employed in combination with the proposed filtering method. The combination is used to filter the synthesizing signals at first. For the filtering of the simulation signal, the filtering effect is compared under conditions of different ensemble number, sampling frequency, and the input signal-noise ratio, respectively. Results show that CEEMDAN outperforms other signal filtering methods. In particular, this method is successful in filtering the friction signal as evaluated by the de-trended fluctuation analysis (DFA) algorithm.

1. Introduction

Understanding the application of the tribological interaction between two bodies in the application of engineering is important. Friction plays an important role in vehicle tires and road construction. The research on tire friction has been going on for decades and has resulted in some classical references and working models. The most frequently used tire design model is probably Pacejka’s “Magic Formula” to evaluate the friction between tire and road [1]. In 1965, Savkoor [2] introduced a simple phenomenological approach to study the variation of the frictional force and viscoelastic properties. This method does not require a complicated formulation of rate processes. However, the method is limited to steady-state conditions and neglects the influence of frictional heating. More recently, references [3,4] employed the car tire as a ‘sensor’ to estimate the friction with the use of neural networks. However, neural networks are computationally expensive. In a recent study, references [5] and [6] use the longitudinal tire force and the signal fusion method to obtain the car tire-road friction coefficient, respectively. These methods, however, all focus on the study of the friction behavior on car tires. Only a few studies have analyzed the friction force between airplane tires and the runway surface. To expand research on the tire mechanics, an experimental rig was designed which measures the friction force between an airplane tire and the runway surface. The friction signal, which features spikes of various amplitudes and noise, is non-stationary and highly non-linear. These qualities make the identification of friction parameters difficult. Thus, a filtering method was developed for this work to reduce the noise and improve signal quality.

Although the traditional filters, such as the Wiener filter [7], are easy to design, most are not suitable for analyzing data derived from a non-stationary and non-linear system. To overcome the drawback, non-linear methods such as wavelet filtering are introduced [8]. However, noise affects the quantification of wavelet coefficients. The wavelet threshold method, which is capable of filtering signals, can solve this problem [9]. However, the method requires the pre-definition of the wavelet basis functions. In essence, its filtering process is not adaptive. Recently, Wu and Huang have developed empirical mode decomposition (EMD) to analyze the data from non-stationary and non-linear systems [10]. This algorithm decomposes the signal into a series of “well-behaved” oscillatory functions, which are known as the intrinsic-mode functions (IMFs). The powerful adaptive EMD tool behaves as a dyadic filter bank [11] and is useful in filtering out the noise in the measurement domains [12,13]. However, EMD has some disadvantages, such as mode mixing [14]. Oscillations of different amplitudes are found in a mode or similar oscillations are encountered in different modes. To avoid this problem, Wu and Huang [15] proposed ensemble EMD (EEMD), a method based on the EMD algorithm. The proposed method follows a study of the statistical characteristics of white noise, involves a noise-assisted analysis, and adds white noise of a uniform frequency distribution into EMD to avoid mode mixing. At present, many EEMD-based filtering methods [16,17] are available. However, the EEMD brings new problems, as the added white noise is not eliminated fully, and different modes may be produced by the interaction between signal and noise. To resolve these issues, the complementary ensemble empirical mode decomposition (CEEMD) was introduced [18]. By adding positive and negative white noises into the signal, the signal is subsequently decomposed by EEMD. The final IMFs can be obtained by averaging the IMFs produced in the EEMD decomposition for signals with added positive and negative white noises. Nevertheless, this method requires a high computational cost and does not resolve the additional modes. Thus, the complete EEMD with adaptive noise (CEEMDAN) was proposed [19]. This method reduces computational load and overcomes additional modes.

Several studies focused on the EMD- [20,21] and EEMD-based [16,17] hybrid filtering methods. To the best of the authors’ knowledge, however, no research has been published on the CEEMD- or CEEMDAN-based hybrid filtering methods. Here, the EMD is not used to filter because of mode mixing issues. In this paper, a novel filtering method is proposed. First, the original signal is decomposed by EEMD, newly proposed CEEMD, or newly proposed CEEMDAN to obtain IMFs. Subsequently, the filtered signal is embodied by new waveforms, which are obtained based on the difference between the original signal and the accumulation sum of IMFs. The simulation signal and friction signal are filtered by the proposed method, respectively. The friction signal between the airplane tire and the runway is recorded during a simulated airplane touchdown. With this filtering method, EEMD, CEEMD, and CEEMDAN are compared according to their ability to filter out the simulation signal. For the friction signal, Discrete Wavelet Transform (DWT) filtering and these filtering methods are compared. For the simulation signal, the filtering effect is evaluated from three aspects: different ensemble number, different sampling rate, and different input signal-noise ratio. For the friction signal, the de-trended fluctuation analysis (DFA) algorithm is used to analyze the filtering performance. The result shows that CEEMDAN in combination with the proposed filtering method is advantageous in removing the noise.

The rest of the paper is organized as follows. Section 2 describes EMD and the improved versions. Section 3 illustrates the filtering method. Section 4 presents the results and discussions. Section 5 concludes the paper.

2. EMD and Improved Versions

2.1. EMD Algorithm

In 1998, Huang [10] first proposed empirical mode decomposition (EMD). The following two conditions must be satisfied to derive IMFs.

(a)

In a data set, the number of extreme value and zero-crossings must be equal or differ by one at most.

(b)

At any point, the mean value of the envelope line defined by the local maxima and the local minima is zero.

The IMFs of a signal $s\left(\text{t}\right)$ are obtained using the following steps:

(1)

Identify the positions and amplitudes of all local maxima and local minima in the signal $s\left(t\right)$;

(2)

Create an upper envelope line $u_0\left(t\right)$ and lower envelope line $v_0\left(t\right)$ by cubic spline interpolation of the local maxima and minima;

(3)

Calculate the mean $m_0\left(t\right)$;

$$m_0\left(t\right)=\frac{u_0\left(t\right)+v_0\left(t\right)}{2}$$

(1)

(4)

Obtain the difference $h_0\left(t\right)$ of the signal $s\left(t\right)$ and the mean $m_0\left(t\right)$ as follows:

$$h_0(t)=s(t)-m_0(t)$$

(2)

(5)

Check if $h_0\left(t\right)$ is an IMF that meets the requirements or not. If not, consider $h_0\left(t\right)$ as the new $s\left(t\right)$ and repeat the above process until an IMF is obtained. Let $c_1\left(t\right)=h_{1k}\left(t\right)$, where k is the sifting times. However, continuous repetition to derive IMFs might not be practical. Thus, a critical decision has to be made as to when to apply the stoppage criterion as follows:

$$S_D={\sum }_{t=0}^T{\left[\frac{h_{1\left(k-1\right)}\left(t\right)-h_{1k}\left(t\right)}{h_{1\left(k-1\right)}\left(t\right)}\right]}^2$$

(3)

If the $S_D$ is smaller than the predetermined value ($0.2\le S_D\le 0.3$), the sifting process will be stopped.

Let $r_1\left(t\right)=s\left(t\right)-c_1\left(t\right)$ be the new $\text{s}\left(\text{t}\right)$ and repeat (1) through (5) to obtain the second IMF, denoted as $c_2\left(t\right)$, then $r_2\left(t\right)=r_1\left(t\right)-c_2\left(t\right)$. Repeat (1) through (5) to derive the $N_{th}$IMF finally. The sifting process will be stopped when the criteria is met: the residue $r_n\left(t\right)$ is a monotonic function. Finally, Equation (4) is obtained as follows:

$$\text{s}\left(t\right)={\sum }_{k=1}^n{C}_k\left(t\right)+r_n\left(t\right)$$

(4)

However, some problems in EMD remain unaddressed, among which mode mixing is the most serious.

2.2. EEMD Algorithm

To solve the mode mixing problem, an EEMD algorithm was introduced by Huang [15]. The following are the steps of EEMD decomposition:

(1)

Add a white noise series $n\left(t\right)$ to the analyzed signal $x_1\left(t\right)$ to obtain the new time series $x_2\left(t\right)$.

$$x_2\left(t\right)=x_1\left(t\right)+n\left(t\right)$$

(5)

(2)

Decompose signal $x_2\left(t\right)$ using the EMD algorithm, and obtain the corresponding IMF of each order;

$$x_2\left(t\right)={\sum }_{i=1}^N{c}_i\left(t\right)+r\left(t\right)$$

(6)

(3)

Repeat Steps 1 and 2 with the different white noise series in each trial to obtain the IMFs $c_{ij}\left(t\right)$, where $i$ is the iteration number and j is the mode;

(4)

Calculate the mean of the corresponding IMFs as the final signal IMF;

$$c_j\left(t\right)=\frac{1}{N}{\sum }_{i=1}^N{c}_{ij}\left(t\right)$$

(7)

The amplitude of added white noise $\text{ε}$ and ensemble number N follow the statistical rule of Equation (8) in EEMD decomposition:

$${\epsilon }_n=\frac{\epsilon }{\sqrt{N}}$$

(8)

where ${\epsilon }_n$ is the final standard deviation of error between the input signal and the corresponding IMF(s).

2.3. CEEMD Algorithm

Although EEMD alleviates the effect of mode mixing, noise will remain in the corresponding IMF(s) if the ensemble number is small. To ensure a noise-free IMF, a CEEMD algorithm [18] is introduced as follows:

(1)

Add positive and negative white noise ${\epsilon }^{\pm }\left(t\right)$ into the targeted signal $x\left(t\right)$, and construct two new data sets $x^{+}\left(t\right)$ and $x^{-}\left(t\right)$.

$$x^{+}\left(t\right)=x\left(t\right)+{\epsilon }^{+}\left(t\right)$$

(9)

$$x^{-}\left(t\right)=x\left(t\right)+{\epsilon }^{-}\left(t\right)$$

(10)

(2)

Repeat Step 1, and decompose each new data $x^{+}\left(t\right)$ and $x^{-}\left(t\right)$ using the EMD algorithm;

(3)

Obtain two sets of IMFs for the $x^{+}\left(t\right)$ and $x^{-}\left(t\right)$ signals;

(4)

Obtain the decomposed result by averaging the $c_{ij}$ in Equation (11), where $c_{ij}$ represents the j-th IMF of the i-th iteration.

$$c_j=\frac{1}{2N}{\sum }_{i=1}^{2N}{c}_{ij}$$

(11)

2.4. CEEMDAN Algorithm

The previous method leads to a new problem, which is high computational load in CEEMD decomposition. To reduce the computational cost and retain the ability to eliminate mode mixing, a CEEMDAN algorithm is proposed [19]. The steps of CEEMDAN decomposition are as follows:

(1)

Decompose signal $\text{x}\left(\text{t}\right)+w_0{\epsilon }^i\left(t\right)$ to obtain the first mode by using the EMD algorithm;

$$c_1\left(t\right)=\frac{1}{N}{\sum }_{i=1}^N{c}_1^i\text{ i}\in \left\{1\cdots N\right\}$$

(12)

where $w_0$ is the amplitude of the added white noise, and $\epsilon \left(t\right)$ is the white noise with unit variance.

(2)

Compute the difference signal;

$$r_1\left(t\right)=x\left(t\right)-c_1\left(t\right)$$

(13)

(3)

Decompose $r_1\left(t\right)+w_1{E}_1\left({\epsilon }^i\left(t\right)\right)$ to obtain the first mode and define the second mode by

$$c_2\left(t\right)=\frac{1}{N}{\sum }_{i=1}^N{E}_1\left(r_1\left(t\right)+w_1{E}_1\left({\epsilon }^i\left(t\right)\right)\right)$$

(14)

(4)

For k= 2, …, K, calculate the k-th residue and obtain the first mode. Define the (k+1)-th mode as follows:

$$c_{k+1}\left(t\right)=\frac{1}{N}{\sum }_{i=1}^N{E}_1\left(r_k\left(t\right)+w_k{E}_k\left({\epsilon }^i\left(t\right)\right)\right)$$

(15)

where $E_j\left(·\right)$ is a function to extract the j-th IMF decomposed by EMD.

(5)

Repeat Step 4 until the residue contains no more than two extrema. The residue mode is then defined as:

$$\text{R}\left(\text{t}\right)=\text{x}\left(t\right)-{\sum }_{k=1}^K{c}_k\left(t\right)$$

(16)

Therefore, the signal $\text{x}\left(t\right)$ can be expressed as follows:

$$\text{x}\left(t\right)={\sum }_{k=1}^K{c}_k\left(t\right)+\text{ R}\left(\text{t}\right)$$

(17)

3. Filtering Method

3.1. Mutual Information

Mutual information, which is derived from information theory, is a good indicator of the similarity measure. Generally, a stronger correlation between two time series results in a larger mutual information. This study uses mutual information to filter signal. The joint entropy of random variables X and Y is defined as

$$\text{H}\left(X,Y\right)=-{\sum }_{i}p\left(x=a_i,y=b_i\right)log p\left(x=a_i,y=b_i\right)$$

(18)

For a discrete random variable X with n elements, the entropy of X (Shannon’s entropy [22]) can been expressed as

$$\text{H}\left(\text{X}\right)=-{\sum }_{i=0}^{n}p\left(i\right)logp\left(i\right)$$

(19)

where $p\left(i\right)$ is the probability density function of discrete point $i$ within the variable X. Mutual information is defined as

$$\text{I}\left(X,Y\right)=H\left(X\right)+H\left(Y\right)-H\left(X,Y\right)$$

(20)

where $H\left(Y\right)$ is the entropy of variable Y.

3.2. Identification of Relevant Mode

Consider a signal

$$\text{y}\left(t\right)=x\left(t\right)+n\left(t\right)$$

(21)

where $\text{y}\left(t\right)$ is the original signal, $x\left(t\right)$ is the pure signal, and $n\left(t\right)$ is the noisy signal.

The main idea of the proposed filtering method is the concentration of the noisy modes (only noise modes) on the first modes (high frequency parts); pure signal modes (only signal modes) are the last modes (low frequency parts). Thus, the following decomposition is obtained:

$$\text{y}\left(t\right)={\sum }_{i=1}^{m}IM{F}_i+{\sum }_{i=\text{m}+1}^{N}IM{F}_i$$

(22)

where $m$ is the index of the relevant mode separating noise from signal, and N is the number of modes. IMF can been obtained by EMD or the improved versions. From the $m$-th mode to the N-th mode are the pure signal modes, and the others are the noisy modes in Equation (22). Consequently, Equation (22) is considered oppositely. The sum of IMFs is subtracted through Equations (23) and (24).

$$N{W}_n\left(t\right)=y\left(t\right)-{\sum }_{i=1}^{n}IM{F}_i\text{ n}=\left(1\cdots \text{m}\right)$$

(23)

$$N{W}_n\left(t\right)=y\left(t\right)-{\sum }_{i=1}^{n}IM{F}_i\text{ n}=\left(\left(\text{m}+1\right)\cdots \text{N}\right)$$

(24)

where $N{W}_n\left(t\right)$ is the n-th New Waveform, which is defined as the difference between the original signal and the sum of the first n IMFs.

In Equation (23), NW₁ (the difference between the original signal and the first mode) to NW_m (the difference between the original signal and the first m modes) is similar to the original signal because the noisy modes are subtracted from the original signal. However, NW_(m+1) (the difference between the original signal and the first (m + 1) modes) to NW_N (the difference between the original signal and the first N modes) is different from that of the original signal in Equation (24) because the noisy mode and pure signal mode are all subtracted from the original signal. The relevant mode can be identified by evaluation if the New Waveform changes or not. In the present study, the mutual information of the adjacent new waveform, which starts with the first new waveform, increases. When the mutual information of some new waveform suddenly decreases, index $m$ of the new waveform will be used to separate the noise and pure signal modes. That condition indicates that the modes before $IM{F}_m$ are dominated by the noise, and the others are the pure signal modes. The filtered signal is the $m$-th New Waveform. Hence, the all-noisy modes are subtracted from the original signal. The following are the filtering steps:

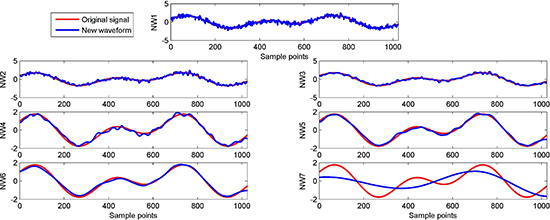
(1)

Obtain the new waveform by the difference between the original signal $\text{y}\left(t\right)$ and the sum of IMFs, respectively.

$$N{W}_n=y\left(t\right)-{\sum }_{i=1}^{n}IM{F}_i\left(\text{n}=1\cdots \text{N}\right)$$

(25)

where N is total number of modes, IMFs are obtained by EMD or improved versions of decomposition, and $N{W}_n$ is the n-th new waveform.

(2)

Calculate the mutual information of adjacent new waveforms:

$${\text{M}}_i=\text{MI}\left(N{W}_i,N{W}_{i+1}\right) \left[i=1\cdots \left(\text{N}-1\right)\right]$$

(26)

where $\text{MI}$ is the abbreviation of mutual information.

(3)

Identify the index of the relevant mode:

$$m=argmax\left({\text{M}}_i\right)+1$$

(27)

(4)

Obtain the filtered signal:

$$\tilde{y}\left(t\right)=N{W}_{\text{m}}$$

(28)

3.3. Application

The original signal is filtered using the proposed method. Signal x(t) is comprised of two periodic signals of differing frequencies.

$$\text{x}\left(t\right)=cos\left(2\pi f_{1}t\right)+sin\left(2\pi f_{2}t\right)$$

(29)

where $f_1$ = 3 Hz and $f_2$ = 6 Hz, and the length of data is 1024.

A white Gaussian noise is added to signal $x\left(t\right)$ with the input signal-to-noise ratio (SNR_in) fixed at 5 dB. Signal $x\left(t\right)$ is decomposed into nine modes. If $x\left(t\right)$ is known, the seventh and eighth modes are two tones of a pure signal. Hence, the first mode to the sixth mode are the noisy modes, whereas the others are the pure signal modes (except for the residue mode). The filtered signal is the sum of the last three modes. Consequently, the New Waveform can be obtained by the difference between the noisy signal and the sum of IMFs via Equations (23) and (24). The new waveform and the original signal are presented in Figure 1.

Only the first seven modes are demonstrated. Figure 1 shows that NW₇ (the difference between the original signal and the first seven modes) is different from the original signal. The reason for such a result is that the new waveform obtained is the difference between the original signal and the sum of the modes (the first six noisy modes and the seventh pure signal mode). Thus, the mutual information between NW₆ (the difference between the original signal and the first six modes) and NW₇ is smaller than the others. Figure 2 illustrates the mutual information between the new waveforms. The numbering-th mutual information in Figure 2 means the mutual information between numbering-th new waveform (the difference between the original signal and the sum of the first numbering IMFs) and the (numbering + 1)-th new waveform (the difference between the original signal and the sum of the first (numbering + 1) IMFs). The mutual information between NW₅ (the difference between the original signal and the first five modes) and NW₆ is the biggest, and that of NW₆ and NW₇ are the smallest. Therefore, NW₆ is the filtered signal. Figure 3 shows the original and filtered signals.

Figure 1. Original signal and new waveforms.

Figure 1. Original signal and new waveforms.

Figure 2. Mutual information of adjacent new waveform.

Figure 2. Mutual information of adjacent new waveform.

Figure 3. Signal filtering: (a) noisy signal and (b) original and filtered signals.

Figure 3. Signal filtering: (a) noisy signal and (b) original and filtered signals.

4. Results and Discussions

With the proposed filtering method, EEMD, CEEMD and CEEMDAN show comparable performances in filtering the simulation signal and the signal to friction measurement.

4.1. Simulation Signal Filtering

Four signals (Bumps, Blocks, Heavysine, and Doppler signals in Figure 4) representative of typical non-linear and non-stationary signals are provided to evaluate the filtering effects of the three filtering methods. The evaluation steps are as follows:

(1)

Compare $SN{R}_{out}$ by using a different ensemble number under the condition that the amplitude of the added white noise is the same.

(2)

Compare $SN{R}_{out}$ using a different sample rate.

(3)

Compare $SN{R}_{out}$ by adding a different input signal-noise ratios ($SN{R}_{in}$) into the original signal, where $SN{R}_{out}$ is the output signal-noise ratio.

Figure 4. Four representative signals.

Figure 4. Four representative signals.

4.1.1. Ensemble Number

Determining the amplitude of white noise and the ensemble number for EEMD, CEEMD, and CEEMDAN is difficult. To achieve a fair comparison of the filtering effect, the same amplitude of added white noise is set in all steps (the amplitude of added white noise is 0.1). Fifteen values for the ensemble number, which range from 10 to 150 with a fixed step of 10, are tested. Figure 4a illustrates the bumps signal (the length of the data is 2048 and those for $SN{R}_{in}$ are 5 dB and 15 dB, respectively). Figure 5a,b is the output signal-noise ratio under conditions of different ensemble numbers. Figure 5 reveals that the output signal-noise ratio obtained through the filtering method based on CEEMDAN is bigger than those derived by the other methods.

Figure 5. The $SN{R}_{out}$ of different ensemble number.

Figure 5. The $SN{R}_{out}$ of different ensemble number.

4.1.2. Different Sampling Rate

Each of the two signals in Figure 4b,c is sampled with five different sampling frequencies, namely 512, 1024, 2048, 4096, and 8192 samples. The $SN{R}_{in}$ values are 3, 5, 8, and 10 dB. Figure 6 and Figure 7a–d show the comparative performance of the filtering methods based on EEMD, CEEMD, and CEEMDAN (the amplitude of added white noise is 0.1, and the ensemble number is 300). In each figure, the filtering method based on CEEMDAN shows the best performance. $SN{R}_{out}$ increases as the sampling frequencies increase. Moreover, the filtering method exhibits a significant improvement in the case where the sampling frequency is high.

Figure 6. The $SN{R}_{out}$ of different sampling frequencies for blocks signal.

Figure 6. The $SN{R}_{out}$ of different sampling frequencies for blocks signal.

Figure 7. The $SN{R}_{out}$ of different sampling frequencies for heavysine signal.

Figure 7. The $SN{R}_{out}$ of different sampling frequencies for heavysine signal.

4.1.3. Different Input Signal-Noise Ratio

Input SNR (SNR_in) ranges from −9 dB to 9 dB with a fixed step of 2 dB (the length of data is 2048). Figure 8 illustrates the plots of SNR_in versus output SNR (SNR_out) where the simulation signal is the Doppler signal (Figure 4d). The SNR_out of the filtering method based on CEEMDAN is higher than those of the other methods.

Figure 8. Doppler signal: SNR_in versus SNR_out.

Figure 8. Doppler signal: SNR_in versus SNR_out.

The result of comparing the filtering effects according to the ensemble number, sampling frequencies, and input signal-noise ratio indicates that the filtering method based on CEEMDAN outperforms the other methods in signal filtering.

4.2. Friction Signal Filtering

To measure the friction that exists between tire and runway during airplane touchdown, an experimental rig was constructed to simulate such events and to record the applied forces. This measurement assembly (Figure 9) is a vertical drop test system consisting of a drop system, an impact platform, support fixtures, a frame, and a tire turning system.

Figure 9. Measurement assembly (1: drop system; 2: frame; 3: support fixtures; 4: tire turning system; 5: impact platform).

Figure 9. Measurement assembly (1: drop system; 2: frame; 3: support fixtures; 4: tire turning system; 5: impact platform).

An important design aspect of this rig is the impact platform. Two force sensors are installed on each side of the test platform (Figure 10) to measure the friction between the tire and runway surface. The signals are acquired by using an eight-channel synchronous data acquisition card with a sampling rate of 110 KHz.

Figure 10. Impact platform system showing various components (1: force sensors; 2: slide; 3: tire; 4: test platform).

Figure 10. Impact platform system showing various components (1: force sensors; 2: slide; 3: tire; 4: test platform).

To reduce noise, the proposed filtering methods are employed to filter for the friction signal of the desired measurement. For comparison purposes, the Discrete Wavelet Transform (DWT, the mother wavelet: db 10, and level of decomposition: 8), which is a widely used method, is used to filter the friction signal. The friction signal corresponds to a drop height of 500 mm, and a rotational speed of 250 rps for the tire. The filtered result is compared with those obtained using EEMD, DWT, CEEMD, and CEEMDAN. The friction signal (Figure 11) exhibits the characteristics of a spiked signal. The waveform fluctuation of the filtering method based on CEEMDAN is less, which implies that CEEMDAN is more appropriate in filtering the friction signal. To quantify the filtering result, a de-trended fluctuation analysis is employed to evaluate the filtering effect. This is presented in the next section.

Figure 11. Comparison of filtering effects: (a) EEMD filtering; (b) DWT filtering; (c) CEEMD filtering; (d) CEEMDAN filtering.

Figure 11. Comparison of filtering effects: (a) EEMD filtering; (b) DWT filtering; (c) CEEMD filtering; (d) CEEMDAN filtering.

Recently, the de-trended fluctuation analysis (DFA) [23,24,25] has been considered a tool of scale and is suitable in analyzing the non-stationary data, especially the fluctuation of time series. The following steps comprise the DFA algorithm:

(1)

Determine the integrated time series:

$$\text{y}\left(\text{k}\right)={\sum }_{i=1}^k\left[x\left(i\right)-\overline{x}\right] \text{k}=1,2,3,\dots ,\text{N}$$

(30)

where $\overline{x}$ is the mean of time series $x\left(i\right)$.

(2)

Divide $\text{y}\left(\text{k}\right)$ into n length segments;

(3)

Determine the local trend ${\text{y}}_n\left(\text{k}\right)$ by using least squares method fitting;

(4)

Obtain fluctuation function $\text{F}\left(n\right)$ by subtracting ${\text{y}}_n\left(\text{k}\right)$ from the integrated time series $\text{y}\left(\text{k}\right)$;

$$\text{F}\left(n\right)={\left(\frac{1}{N}{\displaystyle \sum }_{k=1}^N{\left[y\left(k\right)-y_n\left(k\right)\right]}^2\right)}^{\frac{1}{2}}$$

(31)

(5)

Get different $\text{F}\left(n\right)$ through different length segments;

(6)

Calculate the slope between $\text{logF}\left(\text{n}\right)$ and $\text{log k}$ (the slope is called the fractal scaling index, represented as $\alpha$), which is expressed by a power law as follows:

$$\text{F}\left(n\right)\propto n^{\alpha }$$

(32)

Figure 12 is the fractal scaling index ($\alpha$) derived from calculating the filtered signal using the DFA algorithm. Slope $\alpha$ of the filtered signal based on CEEMDAN is bigger than the other value (Figure 12). A related study [26] indicated that the larger value of slope $\alpha$ results in a smoother time series. Based on the experiment, the CEEMDAN filtering method is more suitable for filtering the friction signal (sparky signal).

Figure 12. Fractal scaling index of four filtering methods.

Figure 12. Fractal scaling index of four filtering methods.

5. Conclusion

A self-adaptive filtering method is developed. The filtering signal makes full use of partial reconstruction. A relevant mode is selected based on the mutual information between adjacent new waveforms (the difference between the noisy signal and the sum of IMFs). EEMD and its extended versions, combined with the proposed filtering method, are employed to filter for the simulation signal. For the simulation signal, the effects of various hybrid filtering methods are assessed by using SNR_out based on (1) ensemble number, (2) sampling frequency, and (3) input signal-noise ratio. For a practical application to a real signal, the friction signal is filtered between a tire and a mock runway surface. Subsequently, the data is obtained using an experimental rig that simulated airplane touchdowns. The filtering results are quantified using the DFA algorithm. The filtering results of the simulation and the real signals show that the filtering method based on CEEMDAN outperforms other filtering methods in terms of reducing noise.