Structures in Sound: Analysis of Classical Music Using the Information Length
Abstract
:1. Introduction
2. Information Variation ( and )
3. Music as a Non-Equilibrium System
4. Results
4.1. Power Law Scalings
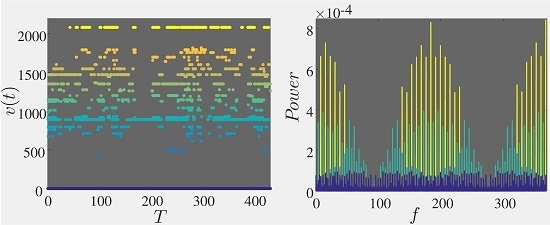
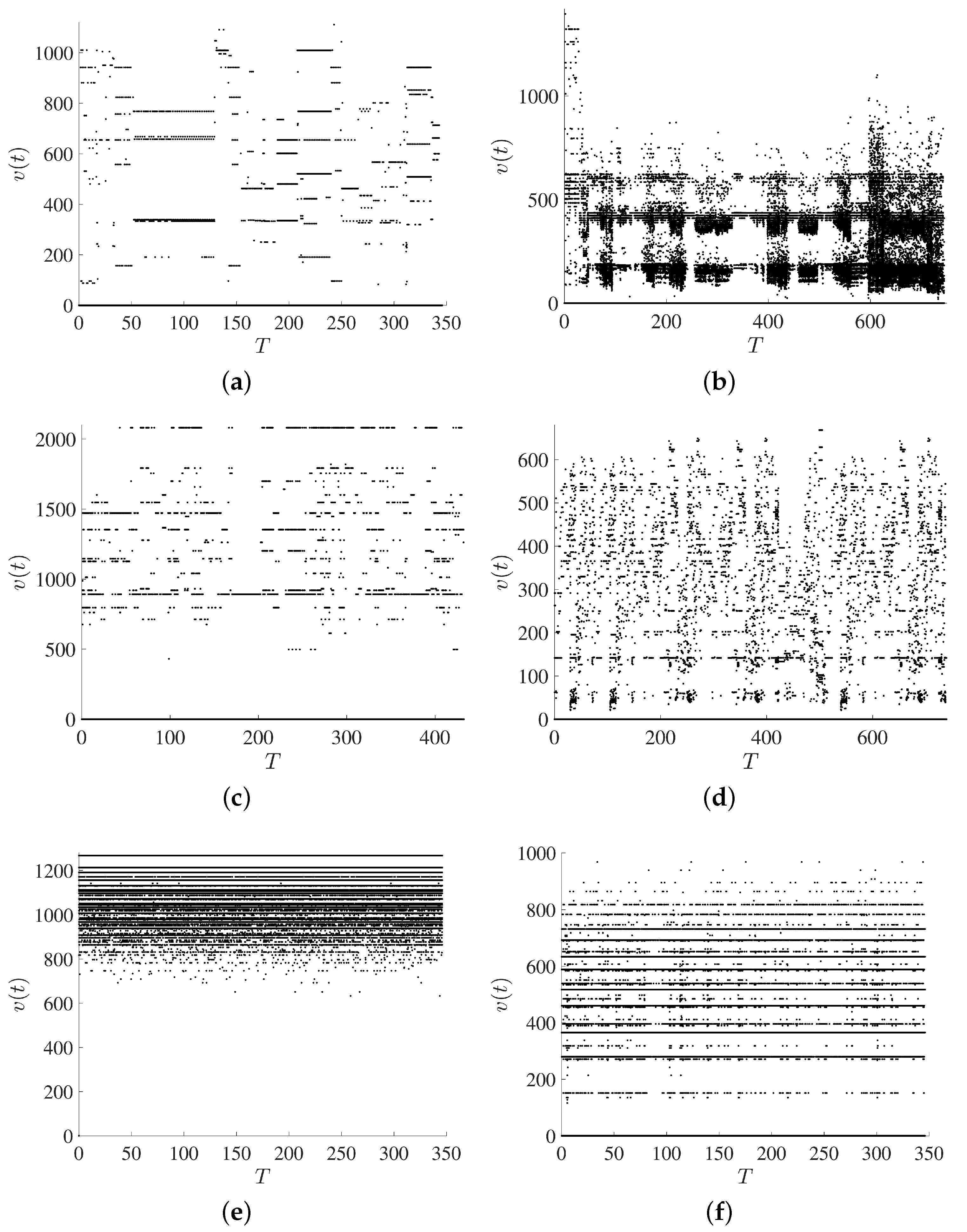
4.2. Velocity
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Du Sautoy, M. The Music of the Primes; Harper Perennial: New York, NY, USA, 2003. [Google Scholar]
- Tzanetakis, G.; Cook, P. Musical genre classification of audio signals. IEEE Trans. Speech Audio Process. 2002, 10, 293–302. [Google Scholar] [CrossRef]
- Madden, C. Fractals in Music: Introductory Mathematics for Musical Analysis; High Art Press: Salt Lake City, UT, USA, 1999. [Google Scholar]
- Manaris, B.; Romero, J.; Machado, P.; Krehbiel, D.; Hirzel, T. Zipf’s law, music classification and aesthetics. Comput. Music J. 2005, 29, 55–69. [Google Scholar] [CrossRef]
- Liu, X.F.; Tse, C.K.; Small, M. Complex network structure of musical compositions: Algorithmic generation of appealing music. Phys. A 2010, 389, 126–132. [Google Scholar] [CrossRef]
- Meyer, L.B. Meaning in Music and Information Theory. J. Aesthet. Art Crit. 1957, 15, 412–424. [Google Scholar] [CrossRef]
- Margulis, E.H.; Beatty, A.P. Musical Style, Psychoaesthetics, and Prospects for Entropy as an Analytic Tool. Comput. Music J. 2008, 32, 64–78. [Google Scholar] [CrossRef]
- Hansen, N.C. Shannon entropy predicts perceptual uncertainty in the generation of melodic pitch expectations. In Proceedings of 12th International Conference on Music Perception and Cognition (ICMPC) and the 8th Triennial Conference of the European Society for the Cognitive Sciences of Music (ESCOM), Thessaloniki, Greece, 23–28 July 2012.
- Hansen, N.C.; Pearce, M.T. Predictive uncertainty in auditory sequence processing. Front. Psychol. 2014, 5, 1052. [Google Scholar] [CrossRef] [PubMed]
- Voss, R.F.; Clarke, J. “1/f noise” in music and speech. Nature 1975, 258, 317–318. [Google Scholar] [CrossRef]
- Serrà, J.; Özaslan, T.H.; Arcos, J.L. Note Onset Deviations as Musical Piece Signatures. PLoS ONE 2013, 8, e69268. [Google Scholar]
- Su, Z.-Y.; Wu, T. Music walk, fractal geometry in music. Phys. A 2007, 380, 418–428. [Google Scholar] [CrossRef]
- Hsü, K.J.; Hsü, A. Self-similarity of the “1/f noise” called music. Proc. Natl. Acad. Sci. USA 1991, 88, 3507–3509. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Wei, J.; Zhang, H.; Xin, J.; Huang, J. A Statistical Physics View of Pitch Fluctuations in the Classical Music from Bach to Chopin: Evidence of Scaling. PLoS ONE 2013, 8, e58710. [Google Scholar] [CrossRef] [PubMed]
- Lebanon, G. Information Geometry, the Embedding Principle and Document Classification. In Proceedings of the 2nd International Symposium on Information Geometry and Its Applications, Tokyo, Japan, 12–16 December 2005.
- Adler, R.; Bazin, M.; Schiffer, M. Introduction to General Relativity; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Anadan, J.; Aharonov, Y. Geometry of Quantum Evolution. Phys. Rev. Lett. 1990, 65, 1697–1700. [Google Scholar] [CrossRef] [PubMed]
- Lanczos, C. The Variational Principles of Mechanics; University of Toronto Press: Toronto, ON, Canada, 1970. [Google Scholar]
- Lesne, A. Statistical Entropy: At the crossroads between probability, information theory, dynamical systems and statistical physics. Math. Struct. Comput. Sci. 2014, 24, e240311. [Google Scholar] [CrossRef]
- Weinhold, F. Metric Geometry of Equilibrium Thermodynamics. J. Chem. Phys. 1975, 63, 2479–2483. [Google Scholar] [CrossRef]
- Rupeiner, G. Thermodynamics: A Riemannian geometric model. Phys. Rev. A 1979, 20, 1608. [Google Scholar] [CrossRef]
- Salamon, P.; Berry, R.S. Thermodynamic Length and Dissipated Availability. Phys. Rev. Lett. 1983, 51, 1127. [Google Scholar] [CrossRef]
- Beck, C. Generalized information and entropy measures in physics. Contemp. Phys. 2009, 50, 495–510. [Google Scholar] [CrossRef]
- Frieden, B. Science from Fisher Information; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Polettini, M.; Esposito, M. Nonconvexity of the relative entropy for markov dynamics: A Fisher information approach. Phys. Rev. E 2013, 88, 012112. [Google Scholar] [CrossRef] [PubMed]
- Feng, E.H.; Crooks, G.E. Far-from-equilibrium measurements of thermodynamic length. Phys. Rev. E 2009, 79, 012104. [Google Scholar] [CrossRef] [PubMed]
- Bordel, S. Non-equilibrium statistical mechanics: Partition functions and steepest entropy increase. J. Stat. Mech. Theory Exp. 2011, 2011, P05013. [Google Scholar] [CrossRef]
- Amari, S.-I. Information Geometry on Hierachy of Probability Distributions. IEEE Trans. Inf. Theory 2001, 47, 1701–1711. [Google Scholar] [CrossRef]
- Wootters, W. Statistical distance in Hilbert space. Phys. Rev. D 1981, 23, 357–362. [Google Scholar] [CrossRef]
- Nicholson, S.B.; Kim, E. Investigation of the statistical distance to reach stationary distributions. Phys. Lett. A 2015, 379, 83–88. [Google Scholar] [CrossRef]
- Braunstein, S.L.; Caves, C.M. Statistical Distance and the Geometry of Quantum States. Phys. Rev. Lett. 1994, 22, 3439–3443. [Google Scholar] [CrossRef] [PubMed]
- Nulton, J.; Salamon, P.; Andresen, B.; Anmin, Q. Quasistatic processes as step equilibrations. J. Chem. Phys. 1985, 83, 334–338. [Google Scholar] [CrossRef]
- Heseltine, J.; Kim, E.-J. Novel mapping in non-equilibrium stochastic processes. J. Phys. A 2016, 49, 175002. [Google Scholar] [CrossRef]
- Kern Scores. Available online: http://kernscores.stanford.edu/ (accessed on 12 July 2016).
- Hänggi, P.; Jung, P. Colored Noise in Dynamical Systems. Adv. Chem. Phys. 1995, 89, 239–326. [Google Scholar]
- Gardiner, C. Stockastic Methods; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Bartosch, L. Generation of colored noise. Int. J. Mod. Phys. C 2001, 12, 851–855. [Google Scholar] [CrossRef]
- Levitin, D.J.; Chordia, P.; Menon, V. Musical rhythm spectra from Bach to Joplin obey a 1/f power law. Proc. Natl. Acad. Sci. USA 2012, 10, 3716–3720. [Google Scholar] [CrossRef] [PubMed]
- Nichols, J.; Flynn, S.W.; Green, J.R. Order and disorder in irreversible decay processes. J. Chem. Phys. 2015, 142, 064113. [Google Scholar] [CrossRef] [PubMed]
- Flynn, S.W.; Zhao, H.C.; Green, J.R. Measuring disorder in irreversible decay processes. J. Chem. Phys. 2014, 141, 104107. [Google Scholar] [CrossRef] [PubMed]





| Octave | Notes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Number | C | C# | D | D# | E | F | F# | G | G# | A | A# | B |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 1 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 2 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |
| 3 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 |
| 4 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 |
| 5 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 |
| 6 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 |
| 7 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 |
| 8 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 |
| 9 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 |
| 10 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 | – | – | – | – |
| T0 (s) | Composition | log | log | ||||
|---|---|---|---|---|---|---|---|
| c | M | R2 | c | M | R2 | ||
| 0.784 | Mozart’s violin Concerto No. 3 | 2.61 | 1.043 | 0.998 | 1.088 | 0.996 | |
| 7.39 | Vivaldi’s Summer | 3.30 | 1.054 | 0.996 | |||
| Beethoven’s 9th Symphony 2nd movement | |||||||
| Tchaikovsky’s 1812 Overture | |||||||
| Mozart piano Concerto No. 3 | |||||||
| Brahms’ string quartet Op.51 | |||||||
| Bach Brandenburg Concerto No. 3 1st movement | |||||||
| Bach Brandenburg Concerto No. 3 2nd movement | |||||||
| Liszt Ballade No. 2 | |||||||
| Chopin Ballade in F Minor, Op. 52 | |||||||
| White noise | |||||||
| correlated noise, | |||||||
| correlated noise, |
| Composer | T0 (s) | m | R2 |
|---|---|---|---|
| Beethoven’s Symphony No.9 1st Mov | 0.7164/−0.0166 | ||
| Mozart’s violin Concerto No. 3 | |||
| Tchaikovsky’s 1812 Overture | |||
| Vivaldi’s Summer | |||
| Mozart’s piano Concerto No. 3 | |||
| Brahm’s string quartet Op. 51 | |||
| Bach Brandenburg Concerto No. 3 1st Mov | |||
| Bach Brandenburg Concerto No. 3 2nd Mov | 0.516/−0.052 | ||
| Liszt Ballade No. 2 | 0.0001 | 0.9975 | |
| Beethoven’s string quartet No. 1 Op. 18 | −0.0123 | 0.9967 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nicholson, S.; Kim, E.-j. Structures in Sound: Analysis of Classical Music Using the Information Length. Entropy 2016, 18, 258. https://doi.org/10.3390/e18070258
Nicholson S, Kim E-j. Structures in Sound: Analysis of Classical Music Using the Information Length. Entropy. 2016; 18(7):258. https://doi.org/10.3390/e18070258
Chicago/Turabian StyleNicholson, Schuyler, and Eun-jin Kim. 2016. "Structures in Sound: Analysis of Classical Music Using the Information Length" Entropy 18, no. 7: 258. https://doi.org/10.3390/e18070258
APA StyleNicholson, S., & Kim, E.-j. (2016). Structures in Sound: Analysis of Classical Music Using the Information Length. Entropy, 18(7), 258. https://doi.org/10.3390/e18070258