Thermoelectrics of Interacting Nanosystems—Exploiting Superselection Instead of Time-Reversal Symmetry

Abstract

Thermoelectric transport is traditionally analyzed using relations imposed by time-reversal symmetry, ranging from Onsager’s results to fluctuation relations in counting statistics. In this paper, we show that a recently discovered duality relation for fermionic systems—deriving from the fundamental fermion-parity superselection principle of quantum many-particle systems—provides new insights into thermoelectric transport. Using a master equation, we analyze the stationary charge and heat currents through a weakly coupled, but strongly interacting single-level quantum dot subject to electrical and thermal bias. In linear transport, the fermion-parity duality shows that features of thermoelectric response coefficients are actually dominated by the average and fluctuations of the charge in a dual quantum dot system, governed by attractive instead of repulsive electron-electron interaction. In the nonlinear regime, the duality furthermore relates most transport coefficients to much better understood equilibrium quantities. Finally, we naturally identify the fermion-parity as the part of the Coulomb interaction relevant for both the linear and nonlinear Fourier heat. Altogether, our findings hence reveal that next to time-reversal, the duality imposes equally important symmetry restrictions on thermoelectric transport. As such, it is also expected to simplify computations and clarify the physical understanding for more complex systems than the simplest relevant interacting nanostructure model studied here.

1. Introduction

1.1. Motivation and General Outline

A thorough understanding of the thermoelectric operation of basic circuit elements such as quantum dots is important for future energy- and information-technologies, see, for example, the review articles [1,2] and references therein. Their nonlinear operation, due to large temperature and voltage gradients, is nontrivial and has only recently received more attention [1,2,3,4,5,6,7,8,9,10,11,12,13], the results indicating new possibilities for thermoelectric applications. To get a better grip on this nonequilibrium regime, the implications of time-reversal symmetry—often exploited in thermoelectrics—have been expressed in fluctuation-relations using the powerful tools of counting statistics [14,15,16,17,18]. This is helpful since in strongly confined devices the coupled nonlinear transport of charge and heat is particularly rich and correspondingly difficult to compute. The reason for this is the energy-dependent transmission caused by the system itself, having discrete quantum states and strong Coulomb interaction, rather than by its coupling. In particular, the effect of Coulomb interaction is multifaceted, since local interactions can both store energy and modify the transfer of energy by individual particles. For applications this can be both damaging and helpful: interaction can limit the efficiency since it provides a way to transfer heat without inducing a charge current, thereby leading to leakage; yet, it can also modify the effective level structure in an advantageous way [6,19] or be used for energy harvesting in multi-terminal devices [20,21,22] as shown experimentally [23,24,25].

One reason why the discussion of efficiencies and performance of thermoelectric devices has been mostly confined to the linear regime of operation is the powerful Onsager reciprocity [26,27,28]. The latter is implied by time-reversal symmetry and it allows to make straightforward statements about efficiencies. However, recently a new general symmetry relation has been discovered for electronic systems [29] that is independent of time-reversal symmetry. Its formulation starts from the very general observation that the dynamics of any system obeying linear superposition of its states is characterized by its time-evolution modes, the right eigenvectors of the evolution generator. The amplitude of excitation of these modes is governed by the corresponding left eigenvectors. For closed systems, these mode and amplitude vectors of the Schrödinger dynamics ${\partial }_t|\varphi \rangle =-iH|\psi \rangle$ are the energy eigenkets and bras, respectively, which are trivially related to each other by taking the Hermitian-adjoint (since $H=H^{†}$). However, for open systems no such simple general relation exists due to the more complicated nature of nonunitary time evolution. Nevertheless, some of us have shown [29] that for any fermionic open system in the wide-band limit, a quite general duality exists between the modes and amplitudes of the time-evolution kernel. This holds even when the reduced density operator of the open system obeys a kinetic equation with the time-nonlocal form ${\partial }_t\rho (t)=-i[H,\rho (t)]+{\int }_0^{t}d{t}^{\prime }\mathcal{W}(t,t^{\prime })\rho (t^{\prime })$. Importantly, the duality relies on a fundamental principle other than time-reversal, namely the superselection rule based on fermion parity [30,31,32,33]. This principle is obeyed by all fermionic systems, and therefore the duality is expected to have far-reaching physical consequences.

For thermoelectric transport, the implications of this additional general principle are to date largely unexplored. Fully exploiting the new duality relation, the present paper revisits the thermoelectric response of a weakly coupled, but strongly interacting single-level quantum dot subject to both electrical and thermal biases, both in the linear and nonlinear regime. We derive new results, significantly clarify known results, and thereby—most notably—outline a completely new approach for the analytical computation of thermoelectrics of interacting nanoscale systems. In References [29,34], it was already realized that the duality relation between decay modes and their excitation amplitudes would naturally express itself in the transient charge and heat currents as the system decays to a new stationary state after a sudden switch (quench). This paper shows that the duality is a similarly powerful tool for the experimentally more accessible stationary thermoelectric transport. Indeed, we demonstrate that both in the linear and nonlinear stationary regime—after some judicious choices—an expansion in open-system evolution eigenmodes is advantageous. The compact analytical formulas we obtain in this way offer several new interesting insights into important measurable thermoelectric transport quantities, and provide a truly nonstandard physical view point. Most importantly and as further outlined below, they expose the remarkable fact that a strongly repulsive system may prominently feature behavior reminiscent of strong attractive interaction in the thermoelectric response coefficients. (This should be clearly distinguished from the effects studied in [35] for systems which from the start have attractive interaction.) Since this was not recognized as such due to lack of a proper framework, our paper does not merely present trivial or subjective rewritings, even though we re-derive and re-express some known results. Instead, our approach is uniquely dictated by the physically-motivated evolution-mode decomposition, and the outcomes are virtually impossible to “guess” without the systematics and new intuition provided by the duality.

We finally note that the very general origin and formulation [29,36,37] of the duality allows us to extend our method beyond the weakly coupled quantum dot setup treated here. As our study illustrates, the technical simplifications can be such that one can avoid numerical calculations altogether. We therefore expect that the ideas presented here can also simplify the analysis of more complex systems studied most recently [11,38,39,40]. This includes situations with broken time-reversal symmetry [34], non-diagonal density operators due to, e.g., noncollinear magnetic fields, and also strongly coupled systems exhibiting time non-local effects.

The paper is structured as follows: after outlining the main ideas and results in general terms in Section 1.2, and introducing the microscopic model and the weak-coupling master equation in Section 2, we review the minimal details of the duality relation that we will exploit for a gated quantum dot coupled to two electronic reservoirs. The mode-decomposition of the charge and energy current formulas (22a) and (22b) are then analyzed in the linear and nonlinear transport regimes in Section 3 and Section 4, respectively. The manuscript also contains an appendix which is substantial, not because the new derivations are complicated, but because the steps are nonstandard and deserve to be outlined.

1.2. Overview of Main Ideas and Results

By discussing a simple, yet relevant model of a nanoscale system, this paper aims to illustrate how the understanding of the role of Coulomb interaction in thermoelectric transport is advanced by the fermion-parity duality. Before going into further details in Section 2.3 it is important to appreciate three of its main ideas in general terms:

(1)

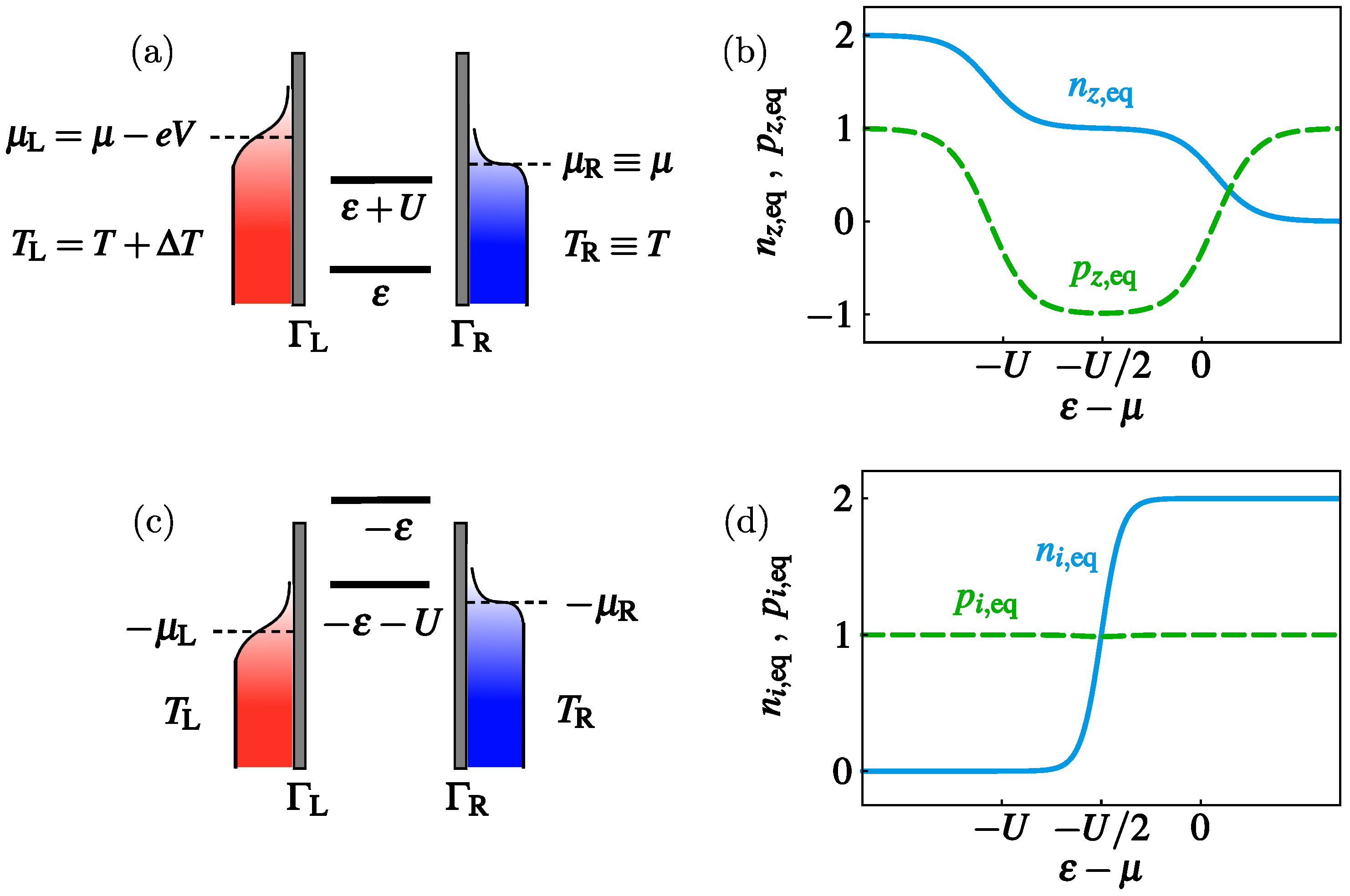
The duality relation maps the eigenmodes of the system of interest to the amplitudes for a different physical system—the dual system. We will refer to the latter as the inverted system because the duality transformation inverts the interaction (as well as other energies), going from repulsive to attractive and vice versa. For quantum dots, this can be easily visualized by inverting the energy landscape in Figure 1a to that of Figure 1c, whose details will be discussed later on. This mapping already explains the seemingly strange occurrence of features of attractive interaction in quantities computed for repulsive systems, as first noted in [29,34]. The straightforward interpretation of such puzzling properties is done resorting to the inverted stationary state, which allows to understand the nontrivial dependence on the original system’s parameters from the—often simple and well-understood [41]—physics of the attractive dual model as in Figure 1c.

(2)

Another reason why the duality clarifies interaction effects is that the “essential” correlating parts of the Coulomb interactions, say, between two orbitals i and j with occupation operators ${\widehat{n}}_i$ and ${\widehat{n}}_j$, respectively, is simply given by parity operators, $(1-2{\widehat{n}}_i)(1-2{\widehat{n}}_j)={(-1)}^{{\widehat{n}}_i+{\widehat{n}}_j}$. In fact, correlated electron model Hamiltonians are often directly formulated in terms of the operators on the left hand side. The duality reveals that the total parity operator always corresponds to a special eigenmode of open fermion-system dynamics [36,37], and is hence protected. In simple yet relevant situations, one thereby cleanly separates, throughout the entire calculation, the contributions of the Coulomb interaction into an “essential” correlating part and a nontrivial “average” contribution carried by a charge mode. Since Coulomb interaction is an important source of energy dependence and energy storage in quantum dots, thermoelectrics is thus seen to be intimately tied up with fermion parity and the corresponding duality.

(3)

Finally, in the context of thermoelectricity, it is important to emphasize that the duality—in the simple form used here—requires energy-independent coupling between system and reservoir (wide-band limit). This does not mean that it is irrelevant to thermoelectric transport, where properly engineered energy-dependence of the coupling can be of interest for the device operation, see, e.g., References [20,21,23,24,25]. Here, the nanoscale system itself provides the strong energy dependence required for thermoelectric effects, both through strong size-quantization and Coulomb interaction. Models of this kind are relevant in many thermoelectric studies [38,42,43,44,45] and the duality applies to their description, even when the energy-independent coupling is strong and the temperature is low [29], cf. [36,37]. Also, effective energy-dependent couplings as realized in multi-dot systems [43,44] can be treated in terms of the duality relation presented here. Finally, the duality considerations can be extended [46] systematically to account for the energy-dependence of the coupling.

As a guide to the present paper, we now outline how the above general points turn up in the specific insights of our study, most of which remain hidden when approaching the thermoelectric problem in the standard way:

In linear response as analyzed in Section 3, we combine the duality with Onsager’s reciprocity derived from time-reversal symmetry. The discussion of the linear response coefficients benefits from the combined insights of both relations [47,48,49,50]. Even more so, in our particular example, we can show how the duality enforces the Onsager relations in linear response, and restricts how these relations break down beyond the linear regime. To achieve this, we first formulate the linear response in a way that is compatible with the duality. Thereby, we find a simple, explicit expression for the average energy carried by electrons, the tight-coupling part of the heat current. Remarkably, it depends on the mean occupation of the dot in the inverted stationary state: this formula exposes the unexpectedly sharp crossover behavior of the thermopower between well-separated resonances as a two-particle resonance in the dual attractive model. Also, the obvious formal similarity between the linear Ohm and Fourier laws,

$$\begin{array}{c}\hfill I=GV,J=K\Delta T\end{array}$$

(1)

gets an unexpected twist: Whereas it is well-known that the stationary-state fluctuations of the dot occupation govern the electrical conductance G, the duality reveals that the linear Fourier heat coefficient $\kappa =K-\Pi SG$, for the heat current in the absence of a charge current, ${J|}_{I=0}=\kappa \Delta T$, is dominated instead by occupation fluctuations in the inverted stationary state. As such, the $ϵ$-dependence of $\kappa$ is also governed by attraction, exhibiting the same two-particle resonance as the thermopower. (The Seebeck coefficient S and the Peltier coefficient $\Pi$ are introduced in Section 3).

The generally more complicated regime of nonlinear response can also be addressed with the duality, as shown in Section 4. For the calculation of the nonlinear Seebeck and Fourier coefficient, we show that an evaluation of equilibrium dot observables—both in the original and dual, inverted system—is often sufficient to obtain the nonequilibrium heat currents. This leads to compact analytical expressions and major simplifications in their explicit calculation, while clarifying the underlying physical picture. For example, the nonlinear Fourier heat is essentially the difference between the parity when the quantum dot is in equilibrium with a single lead on the left or on the right. Although it is well-known that the Fourier heat is carried by electron-electron interaction—even for macroscopic devices [51]—the duality pinpoints precisely which part of the interaction is crucial: it is the parity operator that is entirely responsible for the transferred Fourier heat. Finally, the strong difference between Peltier and Seebeck effects in the nonlinear regime, indicating the breakdown of Onsager reciprocity, can be rationalized completely. The nonlinear Peltier coefficient can be decomposed into an equilibrium Seebeck contribution that stems from the heat transport tightly coupled to the charge transport and a parity-mode contribution. Both of these contributions are sensitive to the attractive-interaction physics of the dual system.

2. Model, Master Equation, and Duality

2.1. Model, Assumptions, and Notation

We are interested in thermoelectric transport through a single-level quantum dot between two reservoirs labeled $\alpha =\mathrm{L},\mathrm{R}$, as sketched in Figure 1a. Many of the following statements can, however, be generalized in a straightforward manner to multiple reservoirs. The full Hamiltonian

$${\widehat{H}}_{\mathrm{tot}}=\widehat{H}+{\widehat{H}}_{\mathrm{leads}}+{\widehat{H}}_{\mathrm{tun}}$$

(2)

decomposes into three parts. The dot Hamiltonian

$$\widehat{H}=\sum _{\sigma =\uparrow ,\downarrow }ϵ{\widehat{n}}_{\sigma }+U{\widehat{n}}_{\uparrow }{\widehat{n}}_{\downarrow }$$

(3)

describes the correlated dynamics of a single spin-degenerate level $ϵ$ with Coulomb charging energy U for doubly occupying the level. Here ${\widehat{n}}_{\sigma }={\widehat{d}}_{\sigma }^{†}{\widehat{d}}_{\sigma }$ are number operators for dot electrons of spin $\sigma =\uparrow ,\downarrow$ with creation (annihilation) operators ${\widehat{d}}_{\sigma }^{†}$ (${\widehat{d}}_{\sigma }$). The quantum dot is coupled to noninteracting electronic reservoirs $\alpha$ described by

$${\widehat{H}}_{\mathrm{leads}}=\sum _{\alpha }{\widehat{H}}_{\alpha }=\sum _{\alpha ,k,\sigma }{ϵ}_{\alpha k}{\widehat{c}}_{\alpha k\sigma }^{†}{\widehat{c}}_{\alpha k\sigma },{\widehat{N}}_{\alpha }:=\sum _{k,\sigma }{\widehat{c}}_{\alpha k\sigma }^{†}{\widehat{c}}_{\alpha k\sigma }$$

(4)

with operators ${\widehat{c}}_{\alpha k\sigma }$ and ${\widehat{c}}_{\alpha k\sigma }^{†}$ for electrons with spin $\sigma$ and orbital quantum number k. The reservoir energies ${ϵ}_{\alpha k}$ and tunneling amplitudes $t_{\alpha k}$ in the tunnel coupling

$${\widehat{H}}_{\mathrm{tun}}=\sum _{\alpha ,k,\sigma }{t}_{\alpha k}{\widehat{d}}_{\sigma }^{†}{\widehat{c}}_{\alpha k\sigma }+\mathrm{h.c.}$$

(5)

are assumed to be spin-independent. We moreover assume that the relevant coupling strengths ${\Gamma }_{\alpha }(E)=2\pi {\sum }_{k\sigma }\delta ({ϵ}_{\alpha k}-E){|t_{\alpha k}|}^2$ determining the typical scale of the tunneling rates are energy independent: ${\Gamma }_{\alpha }(E)\approx {\Gamma }_{\alpha }$. This wide-band limit assumption is crucial for the derivation of the fermion-parity duality in the simple form given below in Equation (13), see also our earlier remarks in Section 1.2 under point (3). Finally, the individual grand-canonical leads $\alpha$ are characterized by the electrochemical potential ${\mu }_{\alpha }$, and the inverse temperature ${\beta }_{\alpha }=1/(k_{\mathrm{B}}{T}_{\alpha })$ entering through the particle/hole Fermi distribution functions $f_{\alpha }^{\pm }(x)={[e^{\pm {\beta }_{\alpha }(x-{\mu }_{\alpha })}+1]}^{-1}$. We let $T=T_{\mathrm{R}}$ and $\mu ={\mu }_{\mathrm{R}}$ denote the global-equilibrium values of the reservoirs and $\Delta T$ and V the applied biases through $T_{\mathrm{L}}=T+\Delta T$ and ${\mu }_{\mathrm{L}}=\mu -eV$.

In the next two sections, we set up the calculation of the stationary charge and heat currents, $I^{\alpha }$ and $J^{\alpha }$, through the quantum dot which can be written in terms of particle and energy currents, $I_{\mathrm{N}}^{\alpha }$ and $I_{\mathrm{E}}^{\alpha }$:

$$\begin{array}{c}\hfill I^{\alpha }=-e{I}_{\mathrm{N}}^{\alpha }\mathrm{and}{J}^{\alpha }=I_{\mathrm{E}}^{\alpha }-{\mu }_{\alpha }{I}_{\mathrm{N}}^{\alpha }.\end{array}$$

(6)

We will outline how to compute the currents $I_{\mathrm{N}}^{\alpha }:=-\frac{\partial }{\partial t}\langle {\widehat{N}}_{\alpha }\rangle$ and $I_{\mathrm{E}}^{\alpha }:=-\frac{\partial }{\partial t}\langle {\widehat{H}}_{\alpha }\rangle$ cf. Equation (4) from lead $\alpha$ into the dot in a way that exploits the duality. From here on, we set $e=k_{\mathrm{B}}=\hslash =1$.

2.2. Master Equation and Non-Equilibrium Currents

Following previous work [29,34,52,53], we outline how to compute the particle and energy currents via the reduced density operator $\widehat{\rho }$ of the quantum dot obtained by tracing out the reservoir degrees of freedom. For weak coupling and high temperatures, ${\Gamma }_{\alpha }\ll T_{\alpha }$, the mixed state obeys a Born-Markov master equation:

$$\frac{d}{dt}|\rho )=W|\rho ).$$

(7)

In Equation (7), operators are written as supervectors, indicated by round kets: $\widehat{\rho }=|\rho )$. In the following we also need to consider the “superhermitian” conjugate of such a supervector $|x)$ which is conveniently written as bra $(x|$. This denotes a linear function acting on any $|y)$, i.e., another operator $\widehat{y}$, as follows: $(x|y):=\mathrm{Tr}[{\widehat{x}}^{†}\widehat{y}]$. In this notation, the kernel W is a superoperator whose specific matrix elements are given in Appendix B for completeness, but which are not required in the following cf. Equation (15). Such a matrix element $(f|W|i)$ physically relates to the rate for a tunnel-induced transition, $|i)\to |f)$, between two of the dot states

$$|0)=|0\rangle \langle 0|,|1)=\frac{1}{2}\left[|\uparrow \rangle \langle \uparrow |+|\downarrow \rangle \langle \downarrow |\right],|2)=|2\rangle \langle 2|.$$

(8)

The empty state $|0\rangle$ has energy $E=0$, the mixture of the spin states $|\uparrow \rangle$ and $|\downarrow \rangle$ has energy $E=ϵ$, and the doubly occupied state $|2\rangle =|\uparrow \downarrow \rangle$ has energy $E=2ϵ+U$. Since the system is fully rotationally invariant [54] and because we focus on the particle- and energy currents, we only need the kernel W in a linear subspace spanned by the three trace-normalized operators given in Equation (8), see the supplement to [29] for details. Importantly, due to the weak coupling, the kernel is the sum of kernels $W_{\alpha }$ that would be obtained if the system was coupled only to reservoir $\alpha$:

$$W=\sum _{\alpha }{W}_{\alpha }.$$

(9)

In the same approximation, the currents $I_{\mathrm{N}}^{\alpha }$ and $I_{\mathrm{E}}^{\alpha }$ can be expressed [34,52] in terms of the reservoir-resolved kernel $W_{\alpha }$, the number operator $\widehat{N}={\sum }_{\sigma }{\widehat{n}}_{\sigma }$, as well as the Hamiltonian $\widehat{H}$ of the dot, and the solution of Equation (7):

$$\begin{array}{c}\hfill I_{\mathrm{N}}^{\alpha }=-\frac{\partial }{\partial t}\langle {\widehat{N}}_{\alpha }\rangle =(N|W_{\alpha }|\rho )\end{array}$$

(10)

$$\begin{array}{c}\hfill I_{\mathrm{E}}^{\alpha }=-\frac{\partial }{\partial t}\langle {\widehat{H}}_{\alpha }\rangle =(H|W_{\alpha }|\rho ).\end{array}$$

(11)

In writing the second equality in Equations (10) and (11), particle and energy conservation have been used. The second step in the energy current (11) is only valid in the weak-coupling limit, see remarks in References [29,52,55]. Regarding the use of the reservoir index $\alpha$, we note that the particle and energy current in reservoir $\alpha$ depend on the properties of all reservoirs. This is in contrast to, e.g., the kernel $W_{\alpha }$, whose contributions are due to a single reservoir $\alpha$ only. We emphasize this difference by choosing superscripts for the former case and subscripts for the latter.

From this point onward, the standard way to obtain the currents in the stationary limit [namely, where the left hand side of Equation (7) equals zero] seems straightforward, knowing the Fermi Golden-Rule expressions for the rates $(f|W_{\alpha }|i)/(f|f)$: (i) Find the non-equilibrium state $|z)$ by solving the stationary limit of Equation (7), $W|z)={\sum }_{\alpha }{W}_{\alpha }|z)=0$ (“zero mode”), and normalize it to $(\mathbb{𝟙}|z)=Tr\left[\widehat{z}\right]=1$; (ii) Plug $|\rho )=|z)$ into the currents (10) and (11). While this procedure yields explicit expressions for the non-equilibrium currents, it often provides only limited analytical and physical insights, in particular for thermoelectric quantities. Moreover, it unnecessarily complicates the evaluation of bias-derivatives required for the linear-response coefficients, even when using Beenakker’s linearization [56,57]. However, inspection of Equations (7), (10) and (11) suggests an alternative route based on our recent results [29,34] which we outline next.

2.3. Fermion-Parity Duality and Its Use in Thermoelectrics

The calculation of the stationary state and the stationary currents

$$\begin{array}{c}\hfill I_{\mathrm{N}}^{\alpha }=(N|W_{\alpha }|z),I_{\mathrm{E}}^{\alpha }=(H|W_{\alpha }|z)\end{array}$$

(12)

are expected to be drastically simplified when expressed in a basis of time-evolution modes, a standard practice when solving linear systems of equations. Looking at Equation (12), three different eigenvector bases suggest themselves: those of the two separate kernels $W_{\alpha }$ ($\alpha =\mathrm{L},\mathrm{R}$) and of the total kernel $W=W_{\mathrm{L}}+W_{\mathrm{R}}$. A key technical point of the present paper is that even though the evaluation of the currents (12) depends on the total kernel W through its zero mode $|z)$, it often turns out that a mode decomposition of the separate kernels $W_{\alpha }$ suffices to compute $|z)$. This provides an important advantage: the kernels $W_{\alpha }$ of the separate leads are by definition always equilibrium kernels. We can thus express and understand nonequilibrium currents in terms of equilibrium quantities which have much simpler dependencies on parameters.

There are three reasons why this decomposition is possible. First, the weak-coupling approximation allows the decomposition given in Equation (9). Second, our study focuses in most parts either on the linear response regime (24), or on the nonlinear regime but with a vanishing average charge current. We will return to this point at the end of this section. The third, most crucial ingredient is the fermion-parity duality, which strongly restricts the form of the kernels W and $W_{\alpha }$ and thereby identifies the optimal variables in which to express the currents.

We first discuss the duality for a quantum dot coupled to only one lead $\alpha$, allowing us to take over the expression for $W_{\alpha }$ given in Reference [29] for this case. There, it was shown that there is a duality relation between the kernel $W_{\alpha }$ and its Hermitian conjugate at inverted energies:

$${\left[W_{\alpha }(\widehat{H},{\mu }_{\alpha })\right]}^{†}=-{\Gamma }_{\alpha }-\widehat{\mathcal{P}}{W}_{\alpha }(-\widehat{H},-{\mu }_{\alpha })\widehat{\mathcal{P}},\widehat{\mathcal{P}}|•)=|{(-\mathbb{𝟙})}^N•).$$

(13)

Here, $W_{\alpha }(-\widehat{H},-{\mu }_{\alpha })$ denotes the kernel of the dual system, in which the signs of all energies in the Hamiltonian $\widehat{H}$, as well as the electrochemical potential ${\mu }_{\alpha }$ in lead $\alpha$, have been inverted. This is sketched in Figure 1a,c. The operator ${(-\mathbb{𝟙})}^{\widehat{N}}$ is the fermion parity of the dot, giving $+1$ for even and $-1$ for an odd occupation number, and its appearance reflects the fundamental origin of the duality, Equation (13). We refer to References [29,52] for an introduction to fermion-parity superselection, the general duality relation and its special form used here, as given in Equation (13).

The duality relation imposes strong restrictions on the fermionic master Equation (7). In fact, these restrictions are so strong that they completely determine the rate matrix $W_{\alpha }$. For illustration, this construction is carried out explicitly in Appendix A and directly produces the three eigenvalues $-{\gamma }_{m\alpha }$ of $W_{\alpha }$ and the corresponding left and right eigenvectors $(m_{\alpha }^{\prime }|$ respectively $|m_{\alpha })$ labeled using $m=z,c,p$:

$$\begin{array}{c}\hfill W_{\alpha }=-\sum _{m=c,p}{\gamma }_{m\alpha }|m_{\alpha })(m_{\alpha }^{\prime }|,\end{array}$$

(14)

where the zero mode ${\widehat{z}}_{\alpha }$ does not show up because ${\gamma }_{z\alpha }=0$. Alternatively, one may directly compute these quantities by diagonalizing the matrix $W_{\alpha }$ employing the duality (13) as done in Reference [29] and obtain:

(15)

Inspecting this table, one explicitly sees that the mode vectors and amplitude covectors are cross-related through the parity operator ${(-\mathbb{𝟙})}^{\widehat{N}}$ and the energy inversion (indicated by subscript “i” on ${\widehat{z}}_{\mathrm{i}\alpha }$ and $n_{\mathrm{i}\alpha }$) that appear in the duality (13). The stationary state—given by the equilibrium grandcanonical ensemble $|z_{\alpha })={\widehat{z}}_{\alpha }=e^{-{\beta }_{\alpha }(\widehat{H}-{\mu }_{\alpha }\widehat{N})}/Tr\left[e^{-{\beta }_{\alpha }(\widehat{H}-{\mu }_{\alpha }\widehat{N})}\right]$ (A4) in the here considered weak tunnel-coupling regime – has the eigenvalue 0. Hence, duality relates $|z_{\alpha })$ to $(p_{\alpha }^{\prime }|$ with eigenvalue $-{\gamma }_{p\alpha }=-{\Gamma }_{\alpha }$, where $(p_{\alpha }^{\prime }|$ is the trace with the inverted stationary state × parity. Similarly, the trace operation $(z_{\alpha }^{\prime }|$ is cross-related to the parity operator $|p_{\alpha })$. Finally, since the Fermi function with respect to any chemical potential ${\mu }_{\alpha }$ obeys $f_{{\mu }_{\alpha }}^{+}(x)=f_{-{\mu }_{\alpha }}^{-}(-x)$, the charge eigenvalue $-{\gamma }_{c\alpha }$ is self-dual and $(c_{\alpha }^{\prime }|$ is mapped to $|c_{\alpha })$.

The crucial point made by the table in (15) is that it reveals the natural variables in which the currents (12) are expressed when inserting the mode expansion (14). These include the expectation values of the charge and parity in the stationary state,

$$\begin{array}{c}\hfill n_z=(N|z)=Tr\left[\widehat{N}\widehat{z}\right],p_z=({(-\mathbb{𝟙})}^N|z)=Tr\left[{(-\mathbb{𝟙})}^{\widehat{N}}\widehat{z}\right],\end{array}$$

(16)

entering through the factors $(m_{\alpha }^{\prime }|z)$. However, due to the factors $(N|m_{\alpha })$ and $(H|m_{\alpha })$, additional expectation values with respect to the reservoir-$\alpha$ resolved equilibrium state (A4) appear:

$$\begin{array}{c}\hfill n_{z\alpha }=(N|z_{\alpha }),p_{z\alpha }=({(-\mathbb{𝟙})}^N|z_{\alpha }),\end{array}$$

(17)

explicitly given as a functions of $ϵ,U,{\mu }_{\alpha },T_{\alpha }$ in Equations (A10) and (A40), and most importantly, expectation values

$$\begin{array}{ccc}\hfill n_{\mathrm{i}\alpha }& =(N|z_{\mathrm{i}\alpha })=n_{z\alpha }\left[ϵ,U,{\mu }_{\alpha }\to -ϵ,-U,-{\mu }_{\alpha }\right],p_{\mathrm{i}\alpha }\hfill & \hfill =({(-\mathbb{𝟙})}^N|z_{\mathrm{i}\alpha })=p_{z\alpha }\left[ϵ,U,{\mu }_{\alpha }\to -ϵ,-U,-{\mu }_{\alpha }\right],\end{array}$$

(18)

where ${\widehat{z}}_{\mathrm{i}\alpha }$ is the corresponding inverted stationary state of the dual system (A7),

$$\begin{array}{c}\hfill {\widehat{z}}_{\mathrm{i}\alpha }={\widehat{z}}_{\alpha }\left[\widehat{H},{\mu }_{\alpha }\to -\widehat{H},-{\mu }_{\alpha }\right]=e^{+{\beta }_{\alpha }(\widehat{H}-{\mu }_{\alpha }\widehat{N})}/Tr\left[e^{+{\beta }_{\alpha }(\widehat{H}-{\mu }_{\alpha }\widehat{N})}\right].\end{array}$$

(19)

In Figure 1b,d, we plot the averages (17) and (18) for $n_{z\alpha }$ and $p_{z\alpha }$ in the right lead, i.e., ${\mu }_{\alpha }=\mu$ and $T_{\alpha }=T$: They are simple, stepped functions of the physical parameters whose shapes are straightforwardly rationalized based on the physics of a repulsive and attractive quantum dot in equilibrium with a single lead $\alpha$, respectively, as explained in the caption to Figure 1. Inverting the interaction U—going from Equations (17) to (18)—qualitatively changes the parameter dependence of these quantities, as shown in the following. We point out that the standard treatment of the problem completely overlooks that expressions (18) are part of the natural variables in which to express the currents (12), and in which to understand the parameter dependence of the transport.

The importance of this insight has been demonstrated for the transient time-dependent response of a quantum dot coupled to a single reservoir in [29]. The final issue that we face in extending this to the stationary nonequilibrium thermoelectric currents (12) is that these currents depend on the stationary state $|z)$ of the system coupled to both leads. This state is the zero mode of the total kernel W, for which the duality holds independently, as shown in Reference [29]:

$${\left[W(\widehat{H},{\mu }_{\mathrm{L}},{\mu }_{\mathrm{R}})\right]}^{†}=-\Gamma -\widehat{\mathcal{P}}W(-\widehat{H},-{\mu }_{\mathrm{L}},-{\mu }_{\mathrm{R}})\widehat{\mathcal{P}},$$

(20)

introducing the lump sum of couplings $\Gamma ={\sum }_{\alpha }{\Gamma }_{\alpha }$.

Importantly, while Equation (20) itself follows from the lead-resolved duality (13) with $W={\sum }_{\alpha }{W}_{\alpha }$, its implications for the eigenvectors of $W=-{\sum }_{m=c,p}{\gamma }_m|m^{\prime })(m|$ and their eigenvalues are nevertheless non-trivial, since $W_{\mathrm{L}}$ and $W_{\mathrm{R}}$ do not commute. The nonequilibrium stationary state that we need is, in particular, not generally a sum of lead-resolved stationary states with some lead-resolved [58] weights ${\lambda }_{\alpha }$,

$$\begin{array}{c}\hfill |z)\ne \sum _{\alpha }{\lambda }_{\alpha }|z_{\alpha }).\end{array}$$

(21)

Section 3 will, however, show that such a simple decomposition does hold when taking the first temperature-bias or voltage-bias derivative Equation (24) at equilibrium. More remarkably, as exploited in Section 4, this decomposition continuous to hold even in the nonlinear regime Equation (51) whenever the system is balanced to maintain zero particle current, $I_{\alpha }=0$ (41). Both cases thus allow us to by-pass the computation of $|z)$ and fully exploit the duality (13) for $W_{\alpha }$ for each lead separately in the way outlined above. This procedure directly ties the non-equilibrium thermoelectric transport to equilibrium physics by introducing the optimal variables (17) and (18) from the start.

2.4. Charge and Energy Currents

Combining all above outlined ideas, we insert the eigenmode decomposition $W_{\alpha }=-{\sum }_{m=z,c,p}{\gamma }_{m\alpha }|m_{\alpha }^{\prime })(m_{\alpha }|$ into the current Equations (12) and use the table in (15) to obtain the central current formulas of the paper:

$$\begin{array}{}\mathrm{(22a)}& I_{\mathrm{N}}^{\alpha }=-{\gamma }_{c\alpha }(c_{\alpha }^{\prime }|z)={\gamma }_{c\alpha }\left[n_{z\alpha }-n_z\right]\hfill \mathrm{(22b)}& I_{\mathrm{E}}^{\alpha }=\left[ϵ+\frac{U}{2}\left(2-n_{\mathrm{i}\alpha }\right)\right]I_{\mathrm{N}}^{\alpha }-{\gamma }_{p\alpha }U(z_{\mathrm{i}\alpha }{(-\mathbb{𝟙})}^N|z).\hfill \end{array}$$

The particle current (22a) is simply the charge relaxation rate × the excess dot charge relative to its equilibrium value with respect to lead $\alpha$, where the current is measured. The energy current (22b) shows a more interesting nonstandard decomposition: it has a tight-coupling contribution directly proportional to the charge current, and a contribution which is independent of the charge current (22a), and hence associated to the parity mode. The prefactor of the tight-coupling term involves the energy scale

$$\begin{array}{c}\hfill E_{\alpha }=ϵ+\frac{U}{2}\left(2-n_{\mathrm{i}\alpha }\right).\end{array}$$

(22c)

Remarkably, the interaction contribution to this energy is not naturally expressed in the stationary state charge $n_{z\alpha }$, but instead in the inverted stationary charge $n_{\mathrm{i}\alpha }$ with respect to lead $\alpha$. As expected, $E_{\alpha }$ is approximately $ϵ$ in the vicinity of transitions between zero- and singly occupied state, and approximately $ϵ+U$ in the vicinity of transitions between singly and doubly occupied state. However, in the crossover regime between these two resonances it is the physics of attractive interaction in $n_{\mathrm{i}\alpha }$ that dominates its behavior, cf. Figure 1.

The overlap $(z_{\mathrm{i}\alpha }{(-\mathbb{𝟙})}^N|z)\approx (z_{\mathrm{i}\alpha }|z)$, contributing to the non-tightly coupled term of Equation (22b), approximately equals a state overlap since the parity in the inverted stationary state is almost always even due to the attractive interaction of the dual model, see Figure 1d. This relation will turn out to be useful for the understanding of the characteristic features of the nonlinear Peltier coefficient discussed in Section 4.2. For explicit numerical results and plots, it is helpful to write

$$(z_{\mathrm{i}\alpha }{(-\mathbb{𝟙})}^N|z)=\frac{1}{4}\left(p_z+p_{i\alpha }\right)+\frac{1}{2}\left(n_z-1\right)\left(n_{i\alpha }-1\right),$$

(22d)

fully expressing it in terms of the measurable quantities introduced in Equations (16) to (18). See, e.g., Reference [53] for the derivation of this relation, and Appendix A, Appendix B, Appendix C for the explicit calculation of all appearing quantities.

The current formulas (22) are valid both in the linear and in the nonlinear response regime and form the starting point of the remainder of the paper. The following sections discuss their implications for the stationary thermoelectric response of the quantum dot from the new perspective offered by the duality (13).

3. Linear Response Regime

We start with the investigation of the linear thermoelectric response of the quantum dot to voltage and temperature gradients, $|V|,|\Delta T|\ll T$. In this case, we can consider the symmetrized charge and heat currents, $I=(I^{\mathrm{L}}-I^{\mathrm{R}})/2$ and $J=(J^{\mathrm{L}}-J^{\mathrm{R}})/2$ which are standardly written in terms of the Onsager matrix,

$$\begin{array}{c}\hfill \left(\begin{array}{c}I\\ J\end{array}\right)\approx \left(\begin{array}{cc}{L}_{11}& L_{12}\\ L_{21}& L_{22}\end{array}\right)\left(\begin{array}{c}V/T\\ \Delta T/T^2\end{array}\right).\end{array}$$

(23)

Here, the diagonal elements $L_{11}=TG$ and $L_{22}=T^{2}K$ present the electric and thermal conductances, ${G=dI/dV|}_{\mathrm{eq}}$ and ${K=dJ/d\Delta T|}_{\mathrm{eq}}$ respectively, whereas the off-diagonal elements $L_{12}=T^2{\partial I/\partial \Delta T|}_{\mathrm{eq}}$ and $L_{21}{=T\partial J/\partial \Delta T|}_{\mathrm{eq}}$ characterize the thermoelectric and the electrothermal responses. Here and below, we denote the evaluation of any quantity q in the equilibrium limit by either of the expressions ${q|}_{\mathrm{eq}}=q_{\mathrm{eq}}{:=q|}_{V=\Delta T=0}$. The linearization of our general result (22) for the currents around equilibrium is conveniently found from

$$\begin{array}{c}{\left.\frac{d}{dx}|z)\right|}_{\mathrm{eq}}=\sum _{\alpha }\frac{{\Gamma }_{\alpha }}{\Gamma }{\left.\frac{d}{dx}|z_{\alpha })\right|}_{\mathrm{eq}}=-\sum _{\alpha }\frac{{\Gamma }_{\alpha }}{\Gamma }\left[\frac{d{\widehat{A}}_{\alpha }}{dx}-(\frac{d{A}_{\alpha }}{dx}|z_{\alpha })·\mathbb{𝟙}\right]·{\left.|z_{\alpha })\right|}_{\mathrm{eq}}\hfill \end{array}$$

(24)

for derivatives with respect to $x={\mu }_{\alpha },{\beta }_{\alpha }$, where we have introduced the affinities ${\widehat{A}}_{\alpha }:={\beta }_{\alpha }\left(\widehat{H}-{\mu }_{\alpha }\widehat{N}\right)$. The derivation of this result in Appendix C.1 only involves the linearization around equilibrium and nothing else, i.e., no detailed balance or other balancing relations used in previous derivations [56,57] and their extensions [11]. Formulating the linear response on the level of the stationary state has the crucial advantage that it can be combined with the duality. Thereby we can circumvent the cumbersome process of taking derivatives of expectation values and subsequently simplifying them. We instead exploit Equation (24), the mode expansion given in (15) and two simple orthogonality relations involving the equilibrium state of the original and the inverted model,

$$(z_{\mathrm{i},\mathrm{eq}}{(-\mathbb{𝟙})}^N|z_{\mathrm{eq}})=0,(z_{\mathrm{i},\mathrm{eq}}{(-\mathbb{𝟙})}^N·N|z_{\mathrm{eq}})=0.$$

(25)

The first is simply the orthogonality of left eigenvector $(p^{\prime }|$ and right stationary vector $|z)$, here applied at equilibrium, which by duality even holds beyond linear response. The second relation follows from ${\widehat{z}}_{\mathrm{eq}}=e^{-(\widehat{H}-\mu )/T}/Tr[e^{-(\widehat{H}-\mu )/T}]$ which for the inverted equilibrium state implies ${\widehat{z}}_{\mathrm{i},\mathrm{eq}}(\widehat{H},\mu )={\widehat{z}}_{\mathrm{eq}}(-\widehat{H},-\mu )\propto e^{(\widehat{H}-\mu )/T}\propto {({\widehat{z}}_{\mathrm{eq}})}^{-1}$. Therefore the second relation is found from

$$\begin{array}{c}\hfill (z_{\mathrm{i},\mathrm{eq}}{(-\mathbb{𝟙})}^N·N|z_{\mathrm{eq}})\propto Tr[\widehat{N}{(-\mathbb{𝟙})}^{\widehat{N}}]=0.\end{array}$$

(26)

Using the above equations, we finally obtain the linear response coefficients of the charge and heat currents (22) (see Appendix C for the details of this non-standard derivation),

$$\begin{array}{}\mathrm{(27a)}& \hfill L_{11}& =& \frac{{\Gamma }_{\mathrm{L}}{\Gamma }_{\mathrm{R}}}{{\Gamma }^2}{\gamma }_{c,\mathrm{eq}}\delta n_{z,\mathrm{eq}}^2\hfill \mathrm{(27b)}& \hfill L_{12}=L_{21}& =& -L_{11}\left[\left(ϵ-\mu \right)+\frac{U}{2}\left(2-n_{\mathrm{i},\mathrm{eq}}\right)\right]\hfill \mathrm{(27c)}& \hfill L_{22}& =& L_{11}{\left[\left(ϵ-\mu \right)+\frac{U}{2}\left(2-n_{\mathrm{i},\mathrm{eq}}\right)\right]}^2+\frac{{\Gamma }_{\mathrm{L}}{\Gamma }_{\mathrm{R}}}{{\Gamma }^2}{\gamma }_{p,\mathrm{eq}}{\left(\frac{U}{2}\right)}^2\delta n_{z,\mathrm{eq}}^2\delta n_{\mathrm{i},\mathrm{eq}}^2,\hfill \end{array}$$

with equilibrium decay rates ${\gamma }_{c,\mathrm{eq}}=\frac{\Gamma }{2}\left[f^{+}(ϵ)+f^{-}(ϵ+U)\right]$ and ${\gamma }_{p,\mathrm{eq}}=\Gamma ={\gamma }_p$. These results warrant a detailed discussion given in the following sections. However, what is immediately clear is that even in the linear response regime, the natural quantities in which the response coefficients are expressed are not only the coupling asymmetry ${\Gamma }_{\mathrm{L}}{\Gamma }_{\mathrm{R}}/{\Gamma }^2$, the expected energies ($ϵ$, $\mu$, U) and the occupation number $n_{z,\mathrm{eq}}$ and its fluctuations in the original dot model,

$$\begin{array}{ccc}\hfill \delta n_{z,\mathrm{eq}}^2& =& {\langle {\widehat{N}}^2\rangle }_{\mathrm{eq}}-{\langle \widehat{N}\rangle }_{\mathrm{eq}}^2=(N^2|z_{\mathrm{eq}})-(N|z_{\mathrm{eq}}{)}^2.\hfill \end{array}$$

(28)

In addition, the occupation number $n_{\mathrm{i},\mathrm{eq}}$ cf. Equation (22c) and its fluctuations

$$\begin{array}{ccc}\hfill \delta n_{\mathrm{i},\mathrm{eq}}^2& =& {\left.\left[{\langle {\widehat{N}}^2\rangle }_{z_{\mathrm{i}}}-{\langle \widehat{N}\rangle }_{z_{\mathrm{i}}}^2\right]\right|}_{\mathrm{eq}}=(N^2|z_{\mathrm{i},\mathrm{eq}})-(N|z_{\mathrm{i},\mathrm{eq}}{)}^2=\delta n_{z,\mathrm{eq}}^2\left[ϵ,U,\mu \to -ϵ,-U,-\mu \right]\hfill \end{array}$$

(29)

in the equilibrium state of the dual, attractive system ${\widehat{z}}_{\mathrm{i},\mathrm{eq}}$ appear as well. They enter via the overlap of the equilibrium state and dual equilibrium state, $(z_{\mathrm{i},\mathrm{eq}}|z_{\mathrm{eq}})=\delta n_{\mathrm{i},\mathrm{eq}}^2·\delta n_{z,\mathrm{eq}}^2$, as proven in Appendix C.4. In Figure 2, we plot the $ϵ$-dependence of both fluctuations by evaluating the explicit expression of $\delta n_{z,\mathrm{eq}}^2$ as a function of $ϵ,U,\mu ,T$, stated in Equation (A41). These fluctuations show peaks at $ϵ=\mu$ and $ϵ+U=\mu$ for the original model and at $ϵ+U/2=\mu$ for the dual attractive model. Using that the fluctuations also follow from an $ϵ$-derivative of the equilibrium occupation numbers (A42), $\delta n_{z,\mathrm{eq}}^2=-T\partial n_{z,\mathrm{eq}}/\partial ϵ$ and $\delta n_{\mathrm{i},\mathrm{eq}}^2=T\partial n_{\mathrm{i},\mathrm{eq}}/\partial ϵ$ due to Equation (29), the observed resonances in $\delta n_{z,\mathrm{eq}}^2$ and $\delta n_{\mathrm{i},\mathrm{eq}}^2$ are readily understood from $n_{z,\mathrm{eq}}$ and $n_{\mathrm{i},\mathrm{eq}}$ as shown earlier in Figure 1b,d.

3.1. Electric Response

For reference, we note that the linear electric conductance

$$\begin{array}{c}\hfill G=\frac{L_{11}}{T}=\frac{1}{T}\frac{{\Gamma }_{\mathrm{L}}{\Gamma }_{\mathrm{R}}}{{\Gamma }^2}{\gamma }_{c,\mathrm{eq}}\delta n_{z,\mathrm{eq}}^2\end{array}$$

(30)

is essentially the charge-relaxation rate ${\gamma }_{\mathrm{c},\mathrm{eq}}$ × the equilibrium charge fluctuations $\delta n_{z,\mathrm{eq}}^2$ plotted in Figure 2. It shows the well-known Coulomb peaks [56] whenever fluctuations of the charge by one electron are energetically allowed, see Figure 1b. Starting from the charge current formula (22a), we note that the conductance (30) derives from the charge-mode of the evolution, as physically expected.

3.2. Thermo-Electric Response and Seebeck Thermopower

The charge mode also solely determines the response (27b) of the charge current to a small temperature difference $\Delta T$. To tie this to an energy scale, we consider the thermopower or Seebeck coefficient $S=-\frac{1}{T}\frac{L_{12}}{L_{11}}$ corresponding to the induced thermo-voltage ${V|}_{I=0}$ across the two leads in the absence of a charge current, ${V|}_{I=0}=S\Delta T$ (Seebeck effect). The expression $E_{\mathrm{eq}}:=TS$ has the unit of an energy, related to the voltage required to counterbalance the thermally induced charge current [59,60]. Our linearized result (27b) gives for this energy

$$\begin{array}{c}\hfill E_{\mathrm{eq}}=TS=\left(ϵ-\mu \right)+\frac{U}{2}\left[2-n_{\mathrm{i},\mathrm{eq}}(ϵ-\mu ,U,T)\right]=E_{\alpha }{|}_{\mathrm{eq}}.\end{array}$$

(31)

Before discussing this result, we immediately note that $E_{\mathrm{eq}}$ equals the tight-coupling energy (22c) [for $n_{\mathrm{i}\alpha }{|}_{\mathrm{eq}}=n_{\mathrm{i},\mathrm{eq}}$ with ${\mu }_{\alpha }=\mu ,T_{\alpha }=T$] which by duality naturally appears in the decomposition of the heat current (22b). As we will detail when introducing the Peltier coefficient in Section 3.3, this fact indicates that the Onsager relation $L_{12}=L_{21}$ is obeyed. However, since we purposely refrain from using time-reversal symmetry, it is first of interest to see how, by using only linear response of the state (24) and the mode-amplitude duality (15), the charge current formula (22a)—apparently of very different form from the heat current—produces nonetheless the same energy scale. This follows by noting that for the linear response coefficient $L_{12}$, only equilibrium correlators are relevant [61], in particular ${\langle \widehat{H}\widehat{N}\rangle }_{\mathrm{eq}}$. latter [62,63] introduces the characteristic energy $E_{\mathrm{eq}}$: as a consequence of the orthogonality relations (25), the only contribution to ${\langle \widehat{H}\widehat{N}\rangle }_{\mathrm{eq}}$ comes from the part of the energy $\widehat{H}$ that does not couple to the parity ${(-\mathbb{𝟙})}^{\widehat{N}}$ see Appendix C.3. The additional appearing correlator ${\langle {\widehat{N}}^2\rangle }_{\mathrm{eq}}$ is responsible for the $\mu$-shift occurring in $E_{\mathrm{eq}}$.

The energy (31) thus naturally appears by mode decomposition of these correlators, showing that the duality is essential for the understanding of the thermopower. As we noted above Equation (22), the interaction-induced part in $E_{\mathrm{eq}}$, respectively S is governed by the behavior of the average occupation $n_{\mathrm{i},\mathrm{eq}}$ in the inverted stationary state. Importantly, this energy is not simply the noninteracting part [$n_{\mathrm{i},\mathrm{eq}}$ depends nontrivially on U, cf. Equation (A10)] or a mean-field-like energy which would involve the average $n_{z,\mathrm{eq}}/2$ rather than $(2-n_{\mathrm{i},\mathrm{eq}})/2$.

In Figure 3a, we plot the Seebeck coefficient, Equation (31), as a function of the energy level position $ϵ-\mu$. The sawtooth behavior has been known for a long time [57] and it is traditionally understood as follows: Each linear branch of the curve is explained by considering just one of the two Coulomb resonances and ignoring the other. For each branch, the magnitude of the voltage that can be sustained increases linearly [64] with $ϵ-\mu$. The shape of the whole curve is then understood as a crossover from the particle-dominated transport of one resonance to the hole-dominated transport of the next one when changing $ϵ-\mu$: by a continuity argument the curve must cross zero between the two resonances to connect the two branches. However, it remains unclear from this line of arguing whether this is a sharp jump—as here in the linear regime—or a smooth crossover—as in the nonlinear regime discussed later. Moreover, close inspection shows that this sharp jump has an anomalous thermal broadening by half the temperature, $T/2$.

Both issues are readily understood from our result (31) deriving from duality: the mean energy $E_{\mathrm{eq}}$ probed by the thermopower depends on the average charge $n_{\mathrm{i},\mathrm{eq}}$ of the quantum dot with inverted energies at equilibrium. As Figure 1c,d illustrate, the occupation in the inverted stationary state $n_{\mathrm{i},\mathrm{eq}}$ abruptly drops from 2 to 0 once $ϵ-\mu$ exceeds $-U/2$, as is well-known for impurities with attractive Coulomb interaction [41]. The duality thus explains the unexpectedly sharp jump in the thermopower in Figure 3. Moreover, since for $U\gg T$ the occupation for the strongly attractive dual model is well-approximated by

$$n_{\mathrm{i},\mathrm{eq}}\approx 2f^{-}(2ϵ+U)=2{\left.f^{-}\left(ϵ+\frac{U}{2}\right)\right|}_{T\to T/2},$$

(32)

we see that the anomalous thermal scale of half the reservoir temperature $T/2$ appears. This has an intuitive interpretation in the dual model: since the attractive interaction favors a single transition involving an electron pair, each electron feels half of the thermal noise. Note that in our calculation for the attractive dual model, two electrons enter sequentially (in time) by two separate processes with rates described by Fermi functions. Their net effect is that the transition becomes allowed at a single value of $ϵ-\mu =-U/2$. Moreover, the electron pairs here are not coherently transported, in other words the rate matrix (A22) contains no nonzero rate connecting the empty and doubly occupied state. Coherent pair tunneling appears only in processes of order ${\Gamma }^2$. In the analysis [65] of the rates for such effects a Bose function appears with $2ϵ+U$ in its argument, indicating coherent transport of fermion pairs. Interestingly, we note that this rate as function of $ϵ$ shows the same halving of the thermal noise as discussed in the present paper.

Since our result (31) expresses the thermopower compactly in the natural and well-understood variable $n_{\mathrm{i},\mathrm{eq}}$, we can easily find a simple yet accurate formula for the level positions at which the thermopower achieves a local minimum $({ϵ}_{-})$ and maximum $({ϵ}_{+})$. This requires finding $ϵ$ from the extremal condition

$$\begin{array}{c}\hfill \frac{\partial n_{\mathrm{i},\mathrm{eq}}}{\partial (ϵ/T)}=\frac{2T}{U}.\end{array}$$

(33)

The strong attractive interaction in the dual system relative to the anomalous lower temperature scale $T/2$ makes Equation (32) an excellent approximation to the left hand side of Equation (33), already for $U\gtrsim 5T$. This gives

$$\frac{{ϵ}_{\pm }-\mu }{U}\approx -\frac{1}{2}\mp \frac{T/2}{U}ln\left(\frac{U}{T/2}\right),S({ϵ}_{\pm })\approx \pm \left[\frac{U}{2T}-\frac{1}{2}\left(1+ln\left(\frac{U}{T/2}\right)\right)\right].$$

(34)

Furthermore, the sensitivity of the thermopower to a gate change in the vicinity of these extrema is relevant for applications [66,67]. We see that in the crossover regime, the negative slope is dominated by the interactions $U\gtrsim T$,

$$\begin{array}{c}\hfill {\left.\frac{dS}{dϵ}\right|}_{ϵ-\mu =-U/2}\approx -\frac{1}{T}\left(\frac{U}{2T}-1\right),\end{array}$$

(35)

in contrast to the positive slopes $1/T$ of the two branches associated with isolated resonances. Figure 3b shows that Equations (34) and (35) indeed approximate very well the features of the Seebeck coefficient for different temperatures. Measurements of the Seebeck coefficient of a quantum dot have confirmed this behavior, see for example References [9,68,69,70].

3.3. Peltier Coefficient

The Peltier coefficient ${\Pi :=\partial J/\partial V|}_{\mathrm{eq}}{/\partial I/\partial V|}_{\mathrm{eq}}$ determines the heat current generated per transferred particle by a small voltage bias $|V|\ll T$ alone ($\Delta T=0$). It thus also defines an energy scale and our heat-current formula (22b) gives

$$\begin{array}{c}\hfill \Pi =E_{\mathrm{eq}}.\end{array}$$

(36)

This provides a physically different picture of the energy scale (22c) as compared to the thermopower: it is the characteristic energy carried by electrons across a biased junction. This is reflected by how it is obtained: it is the prefactor of the first, tight-coupling part in the heat current (22b) cf. Equation (31).

Of course, Onsager reciprocity dictates $L_{12}=L_{21}$, i.e., that the values of the energy scales obtained from the electro-thermal and thermoelectric response are the same, where $L_{21}{=T\partial J/\partial V|}_{\mathrm{eq}}$ and $\Pi =-L_{21}/L_{11}$. However, since we explicitly avoid arguing from time-reversal symmetry, it is of interest to see how the reciprocity relation $L_{21}=L_{12}$ emerges when only using our duality (13). The crucial point in our approach is that the fermion-parity part of the energy current (22b), carrying part of the interaction energy, is to linear order insensitive to the bias V for any value of the remaining parameters:

$$\begin{array}{c}\hfill {\left.\frac{d}{d{\mu }_{\alpha }}(z_{\mathrm{i}\alpha }{(-\mathbb{𝟙})}^N|z)\right|}_{\mathrm{eq}}=0.\end{array}$$

(37)

This follows from the linear-response of the stationary state $\widehat{z}$ given in (24) together with the orthogonalities (25) see Appendix C.4. The result (37) thus implies that in linear response to the voltage bias, the heat current coefficient $L_{21}$ stems from the charge mode only, see also Reference [71]. Since this is equally true for the thermopower in $L_{12}$, we indeed reobtain Onsager’s reciprocity relation. We stress in particular that the tight-coupling of the heat- and charge current is not an approximation in our treatment, but follows from duality.

In Section 4, we will see that the parity contribution to heat current (22b) does play a role for finite bias, pinpointing how the interesting deviations between $\Pi$ and S emerge beyond linear response.

3.4. Thermal Response and Fourier Heat Conductance

Finally, the thermal coefficient $L_{22}=T^2{\partial J/\partial \Delta T|}_{\mathrm{eq}}$, given by Equation (27c), acquires contributions from both terms in Equation (22b). This suggests that there are two types of energy fluctuations that correspond to linear thermal transport when a thermal gradient is applied. Indeed, the fluctuation of the grand-canonical energy $\widehat{\mathcal{H}}:=\widehat{H}-\mu \widehat{N}$ determining the equilibrium state ${\widehat{z}}_{\mathrm{eq}}\propto e^{-\widehat{\mathcal{H}}/T}$ decomposes into two corresponding parts:

$$\begin{array}{c}\hfill \delta {\widehat{\mathcal{H}}}_{\mathrm{eq}}^2={\langle {\widehat{\mathcal{H}}}^2\rangle }_{\mathrm{eq}}-{\langle \widehat{\mathcal{H}}\rangle }_{\mathrm{eq}}^2=({\mathcal{H}}^2|z_{\mathrm{eq}})-{\left[(\mathcal{H}|z_{\mathrm{eq}})\right]}^2=E_{\mathrm{eq}}^2\delta n_{z,\mathrm{eq}}^2+{\left(\frac{U}{2}\right)}^2\delta n_{\mathrm{i},\mathrm{eq}}^2\delta n_{z,\mathrm{eq}}^2,\end{array}$$

(38)

see Appendix C.4. Thus, the charge (parity) contribution to the linear heat transport coefficient $L_{22}$ stated in (27c) are the charge- (parity-) related energy fluctuations × the charge (parity) rate ${\gamma }_{\mathrm{c},\mathrm{eq}}$ (${\gamma }_{\mathrm{p},\mathrm{eq}}$).

In thermoelectric applications, one often wants to know the heat transferred from the hot to the cold reservoir when no electrical power is generated. This purely thermal current ${J|}_{I=0}\approx \kappa \Delta T$ for a small thermal bias $\Delta T$ at zero charge current is characterized by the Fourier heat conductance, ${\kappa =\partial J|}_{I=0}{/\partial \Delta T|}_{\mathrm{eq}}$. It is given by $T^2\kappa =L_{22}-L_{12}{L}_{21}/L_{11}$, for which we obtain

$$\begin{array}{ccc}\hfill \kappa & =& \frac{1}{T^2}\frac{{\Gamma }_{\mathrm{L}}{\Gamma }_{\mathrm{R}}}{{\Gamma }^2}{\gamma }_{p,\mathrm{eq}}{\left(\frac{U}{2}\right)}^2\delta n_{z,\mathrm{eq}}^2\delta n_{\mathrm{i},\mathrm{eq}}^2\hfill \end{array}$$

(39)

using Equation (27). This coefficient stems entirely from the parity-mode contribution to the heat current. As in the Drude theory for metals [51], the pure thermal conductance $\kappa$ is due to the electron-electron interaction in our weakly coupled [72] setup. However, we note that the interaction also nontrivially enters into the other term of the heat current that does not contribute to $\kappa$. The heat-current decomposition dictated beforehand by duality thus naturally pinpoints which part of the interaction enters the purely thermal Fourier heat conductance—namely the fermion-parity part. We again stress that both a naive perturbative decomposition of the heat current (noninteracting part + interaction corrections) as well as a mean-field decomposition fail to achieve this.

The duality furthermore clarifies the parameter-dependence of $\kappa$. Being the product of the charge fluctuations in the stationary and in the inverted stationary state, the Fourier coefficient might be expected to reflect the fluctuations $\delta n_{z,\mathrm{eq}}^2$ of the actual system, for example in its $ϵ$-dependence. However, these fluctuations that we plotted in Figure 2 are unable to account for the single resonance that $\kappa$ shows at $ϵ-\mu =-U/2$ in Figure 4. Instead, this peak entirely comes from the fluctuations $\delta n_{\mathrm{i},\mathrm{eq}}^2$ in the dual model, where due to the attractive interaction only a transition from zero and double dot occupation occurs precisely for this level position, cf. Figure 5. Interestingly, the anomalous thermal broadening $T/2$ in the attractive model [Equation (32) ff.] is crucial to make these fluctuations dominate: it leads to a difference in the exponential thermal suppressions of the two fluctuations when $ϵ$ is varied, as shown in the inset of Figure 2. As a result, when multiplying the two curves in Figure 2, the peak (tails) of $\delta n_{\mathrm{i},\mathrm{eq}}^2$ can overcome (suppress) the tails (peaks) of $\delta n_{z,\mathrm{eq}}^2$ and thereby determine the shape of the result for $\kappa$ in Figure 4. The very good approximation to the peak height for $U\gg T$,

$$\begin{array}{c}\hfill \kappa \approx -\frac{{\Gamma }_{\mathrm{L}}{\Gamma }_{\mathrm{R}}}{\Gamma }\frac{\partial }{\partial x}{\left.\tanh \left(\frac{1}{x}\right)\right|}_{x=\frac{4T}{U}}=\frac{{\Gamma }_{\mathrm{L}}{\Gamma }_{\mathrm{R}}}{\Gamma }{\left(\frac{U}{4T}\frac{1}{\cosh \left(\frac{U}{4T}\right)}\right)}^2,\end{array}$$

(40)

will be derived later on in Equation (55), by exploiting the duality directly in the nonlinear regime and linearizing afterwards.

Thus, whereas $\delta n_z^2$ determines the electric dissipation of the electric conductance, the fluctuation of the inverted dot population, $\delta n_{\mathrm{i}}^2$ dominates the thermal dissipation described by Fourier heat. This is the unexpected twist to the formal analogy between Ohm’s law and Fourier law that we announced earlier in Equation (1). It appears only when one examines the origin of their coefficients, Equations (30) and (39), taking into account the fundamental restrictions imposed by duality.

Finally, we show how the duality simplifies the Fourier heat transfer even on a pictorial level. Figure 5a shows how this energy flow can be pictured in the original, repulsive model as a cycle of single-electron tunneling processes, the cycle being restricted to have zero net charge current, $I=0$. Two cycles contribute to the Fourier heat, in which the energy $ϵ$ ($ϵ+U$) is transferred from the cold (hot) lead to the hot (cold) one through the lower (higher) resonance, corresponding to the addition energy for the transition between zero and single occupation (between single and double occupation) of the dot. In either cycle, an amount of energy U is removed from the hot reservoir and released into the cold one. What remains unclear in this picture is how a single sharp peak at $ϵ-\mu =-U/2$ with a thermal broadening given by $T/2$ can emerge due to a delicate cancellation between particle and hole processes which are all off resonant. In Figure 5b we show how (in linear response) the same energy transfer can be understood in the inverted dual model in terms of the single resonance available in an attractive quantum dot which can be either empty or doubly occupied. This process clearly shuts off for $|ϵ+U/2-\mu |\gg T/2$, implying the fluctuations $\delta n_{\mathrm{i},\mathrm{eq}}^2$ vanish and $\kappa$ with it.

4. Nonlinear Regime

In the regime where either of the biases V and $\Delta T$ is large enough to invoke a nonlinear current response, Onsager’s relations are of no help anymore. Although nonlinear fluctuation relations may provide interesting insights [4,73], this would require additional machinery of counting statistics. The fermion-parity duality (13), instead, can be exploited in the nonlinear regime without further ado: it allows us to simplify the derivation and improve our understanding of the nonlinear Seebeck, Peltier, and Fourier coefficients obtained from the full non-equilibrium currents (22). We note that since now heat currents are not anymore conserved due to the finite Joule heating, it is only meaningful to consider lead-resolved heat currents $J^{\alpha }$ for $\alpha =\mathrm{L}$ or R.

4.1. Thermo-Electric Response and Seebeck Thermopower

We start by analyzing the nonlinear thermopower/Seebeck coefficient $S_{\mathrm{nl}}{=V|}_{I=0}/\Delta T$. The required thermo-voltage ${V|}_{I=0}$ is obtained by solving $I=0$ for V using the currents (6). The form of the charge current (22a) shows that this is equivalent to maintaining equal lead-resolved and, therefore, equilibrium occupations on the dot:

$$\begin{array}{c}\hfill n_{z\mathrm{L}}=n_{z\mathrm{R}}.\end{array}$$

(41)

This simplification is ultimately a consequence of the fact that for the spin-degenerate quantum dot model considered here, duality (13) dictates the charge mode to be an exact eigenmode both in and out of equilibrium, see (15). Since we consider ${\mu }_{\mathrm{R}}=\mu$ to be fixed, we can readily solve the balance Equation (41) for ${\mu }_{\mathrm{L}}\equiv \mu -V$ and obtain the nonlinear thermopower, using the explicit expressions for $n_{z\mathrm{L}}$ and $n_{z\mathrm{R}}$ given in Equation (A10) as outlined in Appendix D. While the result could be written in terms of Fermi functions directly, a particularly insightful form is

$$\begin{array}{cc}\hfill S_{\mathrm{nl}}=& \frac{1}{T}\left(ϵ-\mu +U\right)-\frac{T+\Delta T}{\Delta T}ln\left[\frac{1-n_{\mathrm{iR}}+\sqrt{{\left(1-n_{\mathrm{iR}}\right)}^2+exp\left(\frac{U·\Delta T}{T·(T+\Delta T)}\right)·n_{\mathrm{iR}}(2-n_{\mathrm{iR}})}}{2-n_{\mathrm{iR}}}\right],\hfill \end{array}$$

(42)

where $n_{\mathrm{iR}}$ is the $ϵ$-dependent inverted stationary charge number with respect to the reference chemical potential $\mu$ and temperature T in the right lead. The representation in terms of the dual occupation number is motivated by its connection to the linear limit, in which $n_{\mathrm{i},\mathrm{eq}}=n_{\mathrm{iR}}$ governs the interaction-related contribution to the Seebeck coefficient for a fundamental reason. This allows us, in the following, to exploit the simple single-step behavior and anomalous thermal scale $T/2$ of the dual charge (32) in order to further analyze $S_{\mathrm{nl}}$.

Let us first consider small to moderate temperature gradients $0<\Delta T\lesssim T$. Plotting $S_{\mathrm{nl}}$ as a function of $ϵ-\mu$ in Figure 6, we see in the here studied regime $U\gg T$ that the nonlinear thermopower maintains the characteristic $ϵ$-dependent shape from the linear regime, exhibiting in particular the qualitative signature of $n_{\mathrm{iR}}$. The only important impact of the increasing thermal bias $\Delta T$ is that the slope of $S_{\mathrm{nl}}$ at $ϵ+U/2=\mu$ becomes increasingly less negative, and correspondingly, local extrema are less pronounced in Figure 6b. To analytically understand this behavior, we realize that due to $\Delta T\lesssim T$ and due to the sharp step of $n_{\mathrm{iR}}(ϵ)$ around $ϵ-\mu =-U/2$, we can efficiently carry out a linear expansion of Equation (42) in $ϵ-\mu$ by first expanding $S_{\mathrm{nl}}$ in $1-n_{\mathrm{iR}}$ around $1-n_{\mathrm{iR}}=-1,0,1$ for $ϵ-\mu$ close to $0,-U/2,-U$ respectively:

$$\begin{array}{c}\hfill T{S}_{\mathrm{nl}}\approx \left\{\begin{array}{cc}{\displaystyle ϵ-\mu +\frac{U}{2}\left[\frac{T(T+\Delta T)}{U·\Delta T}\left(e^{\frac{U·\Delta T}{T(T+\Delta T)}}-1\right)(2-n_{\mathrm{iR}})\right]\approx ϵ-\mu }\hfill & ,ϵ\approx \mu \hfill \\ \hfill \\ {\displaystyle ϵ-\mu +\frac{U}{2}\left[1+\frac{T(T+\Delta T)}{U·\Delta T/2}\left(1-e^{-\frac{U·\Delta T/2}{T(T+\Delta T)}}\right)(1-n_{\mathrm{iR}})\right]\approx -\frac{T}{T_{\mathrm{eff}}}(ϵ-\mu +\frac{U}{2})}\hfill & ,ϵ+\frac{U}{2}\approx \mu \hfill \\ \hfill \\ {\displaystyle ϵ-\mu +\frac{U}{2}\left[2-\frac{T(T+\Delta T)}{U·\Delta T}\left(e^{\frac{U·\Delta T}{T(T+\Delta T)}}-1\right)n_{\mathrm{iR}}\right]\approx ϵ-\mu +U}\hfill & ,ϵ+U\approx \mu .\hfill \end{array}\right.\end{array}$$

(43)

For $ϵ-\mu$ close to $0,-U$, the flat $ϵ/U$-dependence and the anomalously small thermal broadening of $n_{\mathrm{iR}}$ by $T/2$, see Equation (32), lead to a complete suppression of the $\Delta T$-dependent non-equilibrium terms. By contrast, the sizable linear $ϵ/U$-dependence of $1-n_{\mathrm{iR}}$ with slope $-U/T$ stated in Equation (35) for $ϵ-\mu =-U/2$ does introduce a relevant $\Delta T$-dependence of the slope of $S_{\mathrm{nl}}$ linearized in $ϵ$, given by the inverse effective temperature

$$\frac{1}{T_{\mathrm{eff}}}\stackrel{U\gg T}{\approx }\frac{1}{T}·\left[\frac{T}{\Delta T}-\frac{T+\Delta T}{\Delta T}·exp\left(-\frac{U}{2T}·\frac{\Delta T}{T+\Delta T}\right)\right]\stackrel{\frac{U\Delta T}{T+\Delta T}\gg T}{\approx }\frac{1}{\Delta T}.$$

(44)

As expected, taking the limit $\Delta T\to 0$ in Equation (43) immediately gives back the linear Seebeck coefficient (31). We also note that a useful demarcation of the regime where the second line in Equation (43) is a good approximation is obtained by finding the crossing points of the linear $ϵ$-expansions in all three regimes:

$$\begin{array}{cc}\hfill |ϵ+U/2-\mu |& \lesssim \frac{\Delta T}{T+\Delta T}·\left[1+coth\left(\frac{U}{4T}·\frac{\Delta T}{T+\Delta T}\right)\right]·\frac{U}{4}\stackrel{\frac{U\Delta T}{T+\Delta T}\gg T}{\approx }\frac{\Delta T}{T+\Delta T}·\frac{U}{2}.\hfill \end{array}$$

(45)

The approximations in Equations (43) and (45) will be helpful for the understanding of the nonlinear Fourier coefficient in Section 4.3.

Let us now address larger temperature gradients $\Delta T\gg T$, approaching and exceeding the interaction strength U. An interesting feature of this regime is that the roots of $S_{\mathrm{nl}}(ϵ)$ close to the Coulomb resonances are shifted towards the root at $ϵ-\mu =-U/2$, and that all roots can even merge entirely at this single level-position for large enough $\Delta T$. This both experimentally [9] and theoretically [74] studied effect is captured by the analytic expression (42) of the thermovoltage, as clearly visible in Figure 6c. Our duality makes explicit that there is no reason that the thermopower roots at $ϵ-\mu =0,-U$ should remain fixed; only the position of resonance at $ϵ-\mu =-U/2$ is dictated by the dual model. Indeed, the linear thermopower (31) is not exactly 0 at $ϵ-\mu =0,-U$, although this effect is exponentially suppressed with large interaction $[0<(2-n_{\mathrm{i},\mathrm{eq}})/2\sim e^{-U/T}$ at $ϵ=\mu ]$.

For large temperature gradients $\Delta T/T\gg 1$, the effect can, however, clearly be seen: Figure 6d displays a sizable root shift on the scale $U/2$ as a function of $\Delta T/U$, obtained numerically from Equation (42) for different $T/U$. We also observe that all roots merge at $ϵ-\mu =-U/2$ at a relatively large temperature gradient, which we define as $\Delta T_0/U$. To get an approximate analytical description of this quantity, we start from the condition $d{S}_{\mathrm{nl}}/dϵ=0$ at $ϵ-\mu =-U/2$, which sets the point beyond which only one root can exist. Since this typically happens at large $\Delta T/T$, we can Taylor expand the derivative in $T/\Delta T$ at fixed $T/U$ to analytically solve for

$$\frac{\Delta T_0}{U}\approx \frac{1}{2}\left[\frac{T}{U}exp\left(\frac{U}{2T}\right)-\frac{T}{U}-\frac{1}{2}\right].$$

(46)

Equation (46) is in good agreement with the numerics shown in Figure 6d. Altogether, this confirms that the root shift is observable for achievable temperature gradients as long as the the interaction strength U does not exceed the base temperature T by more than an order of magnitude.

4.2. Electro-Thermal Response and Peltier Coefficient

The nonlinear Peltier coefficient ${\Pi }_{\mathrm{nl}}^{\alpha }=(J^{\alpha }/I^{\alpha }){|}_{\Delta T=0}$ determines the heat transferred per charge in response to a finite voltage bias V ($\Delta T=0$). It therefore quantifies one of the desired thermoelectric effects: the ability of the quantum dot system to electrically cool one of the contacts (via a heat current out of this contact). Due to the absence of heat current conservation under nonequilibrium conditions, the nonlinear Peltier coefficient depends on the lead $\alpha$ that it refers to, ${\Pi }_{\mathrm{nl}}^{\mathrm{L}}\ne {\Pi }_{\mathrm{nl}}^{\mathrm{R}}$, and furthermore differs substantially from the Seebeck coefficient, as we now discuss.

Since the Peltier coefficient, in contrast to the Seebeck and Fourier coefficient, is not restricted by charge-current balancing, we can not express it entirely in lead-resolved equilibrium variables. Nevertheless, we can exploit our duality to a large extent. First, we decompose the Peltier coefficient into a part that stems from the heat current contribution that is tightly coupled to the charge current, ${\Pi }_{\mathrm{nl},\mathrm{ntc}}^{\alpha }$ [first term in Equation (22b)], and the non-tightly coupled contribution, ${\Pi }_{\mathrm{nl},\mathrm{ntc}}^{\alpha }$, stemming from the fermion-parity mode [second term in Equation (22b)],

$$\begin{array}{cc}\hfill {\Pi }_{\mathrm{nl}}^{\alpha }& ={\Pi }_{\mathrm{nl},\mathrm{tc}}^{\alpha }+{\Pi }_{\mathrm{nl},\mathrm{ntc}}^{\alpha }.\hfill \end{array}$$

(47)

The first term of Equation (22b) couples the charge current to $E_{\alpha }$, the average energy (22c). This is the same energy that determines the linear thermopower (Seebeck coefficient), but with respect to ${\mu }_{\alpha }$. Therefore,

$$\begin{array}{c}\hfill {\Pi }_{\mathrm{nl},\mathrm{tc}}^{\alpha }{=TS|}_{\mu \to {\mu }_{\alpha }},\end{array}$$

(48)

and ${\Pi }_{\mathrm{nl},\mathrm{tc}}^{\mathrm{L}}$ is just the linear thermopower curve shifted by the applied bias V, in contrast to ${\Pi }_{\mathrm{nl},\mathrm{tc}}^{\mathrm{R}}$, which is not shifted. This can be seen in Figure 7a,b, where we plot the Peltier coefficient and its decomposition, the dashed curves showing the tight-coupling part. It means that, interestingly, the nonlinear Peltier coefficient, although not related to the nonlinear Seebeck coefficient, is actually related to the linear Seebeck coefficient.

The remaining non-tight-coupling contribution ${\Pi }_{\mathrm{nl},\mathrm{ntc}}^{\alpha }$ is completely due to the parity mode,

$$\begin{array}{c}\hfill {\Pi }_{\mathrm{nl},\mathrm{ntc}}^{\alpha }=-\frac{{\gamma }_{p\alpha }U}{I^{\alpha }}(z_{\mathrm{i}\alpha }{(-\mathbb{𝟙})}^N{|z)|}_{\Delta T=0}.\end{array}$$

(49)

Using Equation (22d), this can be expressed in the average occupation and parity in the stationary state $|z)$ and $\alpha$-resolved inverted stationary state $|z_{\mathrm{i}\alpha })$. In order to make further quantitative progress, the evaluation of the expectation values $n_z$ and $p_z$ with respect to the stationary state $|z)$ cannot be avoided (see Appendix B). However, we stress that Equation (49) together with Equation (22d) already present a significant simplification relative to the standard way of writing the same result.

Moreover, we can still further exploit the duality in a qualitative discussion. For example, the results in Figure 7 show that ${\Pi }_{\mathrm{nl},\mathrm{ntc}}^{\mathrm{L}}$ contributes only in a limited interval of $ϵ$ values. This can be explained using only the observation that this contribution depends on the overlap of the stationary state $\widehat{z}$ and the $\alpha$-resolved inverted equilibrium state ${\widehat{z}}_{\mathrm{i}\alpha }$, as given in Equation (49). Intuitively, this overlap is a measure of how much the two mixed states $\widehat{z}$ and ${\widehat{z}}_{\mathrm{i}\alpha }$ resemble each other, modulo parity signs. Taking ${\mu }_{\mathrm{L}}=\mu -V$, the inverted equilibrium state ${\widehat{z}}_{\mathrm{iL}}$ switches from an empty state for $ϵ-\mu \le -U/2-V$ to a doubly occupied state for $ϵ-\mu \ge -U/2-V$. In contrast, the nonequilibrium stationary state $\widehat{z}$ has a less simple bias dependence and determines the evolution of the panels of Figure 7b, where V was chosen to be negative, $|V|=-V$: (Left): For $|V|\ll U/2$ the overlap (49) is nonzero only at $ϵ+U/2=\mu$ up to thermal broadening. (Center): For $U/2<|V|<U$, there exists a region $ϵ-\mu \in [0,|V|-U/2]$, where the state $\widehat{z}$ is a mixture of an empty and singly-occupied state while the inverted state ${\widehat{z}}_{\mathrm{iL}}$ is empty, leading to a nonzero overlap (49). (Right) For $|V|>U$ there is a double step. Here, the inverted state ${\widehat{z}}_{\mathrm{iL}}$ is empty for all $ϵ-\mu \le |V|-U/2$. The double step in the overlap (49) arises due to the state $\widehat{z}$ being empty with probability $p_0\approx 1/4$ and $1/3$ for $ϵ-\mu \in [0,|V|-U]$ and $[|V|-U,|V|-U/2]$, respectively.

The duality thus allows to understand the stepwise contributions of ${\Pi }_{\mathrm{nl},\mathrm{ntc}}^{\mathrm{L}}$ and thereby the details of Figure 7b: its effect is to shift the tight-coupling part (determined by the Seebeck coefficient, i.e., the “Onsager part”) to lower values for moderate bias $|V|<U$, and to double the saw-tooth behavior for high bias $|V|>U$. Overall, a large bias gives more negative values for ${\Pi }_{\mathrm{nl}}^{\mathrm{L}}$, restricting the regime of effective cooling of the left reservoir to $ϵ-\mu >|V|$, for which heat is carried out of the left reservoir (equivalently, the right reservoir for this setting can only be cooled if $ϵ-\mu <-U$).

4.3. Thermal Response and Fourier Coefficient

Finally, we examine the nonlinear Fourier heat coefficient, ${\kappa }_{\mathrm{nl}}^{\alpha }:=J^{\alpha }{|}_{I=0}/\Delta T$, for lead $\alpha =\mathrm{L},\mathrm{R}$, the ratio of the heat current and the finite temperature bias in the absence of a charge current. Since the Fourier heat is independent of the Joule heating, we have ${\kappa }_{\mathrm{nl}}^{\mathrm{L}}\equiv -{\kappa }_{\mathrm{nl}}^{\mathrm{R}}$ by energy conservation. Our heat current formula (22b) immediately shows that the nonlinear Fourier heat current is produced solely by the parity mode contribution:

$$\begin{array}{cc}\hfill {\kappa }_{\mathrm{nl}}^{\mathrm{L}}& =-{\gamma }_{p\mathrm{L}}\frac{U}{\Delta T}(z_{i\mathrm{L}}{(-\mathbb{𝟙})}^N|z){|}_{I=0}.\hfill \end{array}$$

(50)

In contrast to the expression (49) for the non-tight-coupling contribution to the Peltier coefficient, the above Equation (50) can be fully analyzed in terms of equilibrium quantities, dictated by the duality. We therefore make use of the remarkable fact that under current balanced conditions (41), the full non-equilibrium stationary state $|z)$ simplifies to a sum of the lead-resolved equilibrium states $|z_{\alpha })$:

$${\left.|z)\right|}_{I=0}={\left.\sum _{\alpha }\frac{{\Gamma }_{\alpha }}{\Gamma }|z_{\alpha })\right|}_{I=0}.$$

(51)

This is shown in Appendix D, in fact for any number of leads $\alpha$. With this, we find

$$\begin{array}{cc}\hfill {\kappa }_{\mathrm{nl}}^{\mathrm{L}}& =\frac{1}{4}\frac{{\Gamma }_{\mathrm{L}}{\Gamma }_{\mathrm{R}}}{\Gamma }\frac{U}{\Delta T}{\left.\left(p_{z\mathrm{L}}-p_{z\mathrm{R}}\right)\right|}_{I=0}.\hfill \end{array}$$

(52)

Remarkably, it shows that the nonlinear Fourier heat coefficient can be rationalized in terms of two relatively simple equilibrium observables of the quantum dot, the lead-resolved parities $p_{z\mathrm{L}}$ and $p_{z\mathrm{R}}$. As previously pointed out, the parity $p_{z\mathrm{R}}$ with respect to the right lead, plotted in Figure 8c, simply equals the equilibrium parity $p_{z,\mathrm{eq}}$, since ${\mu }_{\mathrm{R}}=\mu$ and $T_{\mathrm{R}}=T$ are kept fixed in the right lead. This equilibrium parity simply changes sign at both resonances, $ϵ-\mu =0,-U$. In contrast, the required value $p_{z\mathrm{L}}{|}_{I=0}$ is obtained by evaluating the explicit expression (A40) of $p_{z,\mathrm{eq}}=p_{z\mathrm{R}}$ at temperature $T+\Delta T$, and at a chemical potential shifted compared to ${\mu }_{\mathrm{R}}=\mu$ by the nonlinear thermovoltage ${V|}_{I=0}=S_{\mathrm{nl}}\Delta T$, which depends nontrivially on the parameters according to Equation (42):

$$\begin{array}{cc}\hfill p_{z\mathrm{L}}& =p_{z,\mathrm{eq}}\left[\mu \to \mu -S_{\mathrm{nl}}(ϵ-\mu ,U,T)\Delta T,T\to T+\Delta T\right].\hfill \end{array}$$

(53)

In the following, more detailed analysis of Equation (52), we can exploit (53) in the regime of moderate temperature gradients $0<\Delta T<T$. Namely, an inspection of Figure 8c,d shows that the parity with respect to the left lead, Equation (53), is expected to take a constant value, equal to the value of $p_{z\mathrm{R}}=p_{z,\mathrm{eq}}$ at the electron-hole symmetric point but at a different temperature $T+\Delta T$, in a $\Delta T$-dependent range around $ϵ-\mu =-U/2$. And indeed, explicitly evaluating the thermovoltage (42) in the piecewise-linear approximation (43) and for $U\Delta T/(T(T+\Delta T))\gg 1$, we find

$$\begin{array}{c}\hfill p_{z\mathrm{L}}\approx \left\{\begin{array}{cc}{p}_{z\mathrm{R}}\hfill & ,ϵ\approx \mu \hfill \\ p_{z,\mathrm{eq}}\left(ϵ-\mu =-U/2,U,T+\Delta T\right)\hfill & ,ϵ+U/2\approx \mu \hfill \\ p_{z\mathrm{R}}\hfill & ,ϵ+U\approx \mu .\hfill \end{array}\right.\end{array}$$

(54)

With the help of Equations (52) to (54), we can now fully understand the plots of ${\kappa }_{\mathrm{nl}}^{\mathrm{L}}$ as a function of the dot level $ϵ$ as shown in Figure 8a,b for different values of the Coulomb interaction. For increasing thermal bias $\Delta T$, the linear response peak at $ϵ-\mu =-U/2$ (Figure 4) increases in both height and width, depending on the ratio $U/T$. Namely, the broadened peak around $ϵ-\mu =-U/2$ for $U/T=10$ clearly assumes a plateau shape at large values of $U/T$, such as $U/T=30$ in Figure 8b. (With decreasing temperature relative to U, it is interesting how cotunneling corrections modify the plateau.) Now, the approximate expressions for the Fourier coefficient in Equation (54) tell us that there is a difference between the parities $p_{z\mathrm{L}}$ and $p_{z\mathrm{R}}$ only between the two resonances in the regime delimited by condition (45). The width of this regime, $U\frac{\Delta T}{T+\Delta T}$, first increases linearly with $\Delta T\ll T$ and starts to become of order U once $\Delta T\gtrsim T$, as indicated by thin, dashed vertical lines in panels (a) and (b). The difference in parities assumes a constant value in the regime given by $U\Delta T/(T(T+\Delta T))\gg 1$, for which the second line in Equation (54) is valid. As visible in panel (b) of Figure 8, this results in the plateau at the maximum value

$${\kappa }_{\mathrm{nl}}^{\mathrm{L}}=-\frac{{\Gamma }_{\mathrm{L}}{\Gamma }_{\mathrm{R}}}{\Gamma }\frac{U}{4\Delta T}\left[tanh\frac{U}{4(T+\Delta T)}-tanh\frac{U}{4T}\right]\mathrm{for}|ϵ+\frac{1}{2}U-\mu |\lesssim \frac{U}{2}\frac{\Delta T}{T+\Delta T},$$

(55)

increasing with $\Delta T$ as indicated by the different dashed horizontal lines in panel (a) and (b) of Figure 8. Taking the limit $\Delta T\to 0$, we obtain the linear response formula (40) reported in Section 3.4.

5. Conclusions and Outlook

We have shown that besides time-reversal symmetry, our duality involving fermion-parity superselection is a crucial general principle for understanding both the linear and nonlinear thermoelectric transport through strongly interacting electronic nanoscale systems. If one is unaware of this, many computed results seem to reflect model-specific features whereas in reality they are fixed from the beginning by the physical restrictions imposed by duality.

Our study illustrates that thermoelectrics is not only interesting for future applications, but also provides new ways in which fundamental effects can be studied: thermal transport properties are particularly susceptible to effects tied to the new duality, since the Coulomb interaction is an additional channel for storing and transporting energy. This naturally brings the fermion-parity operator into the problem, which is an open-system evolution mode that is fundamentally “protected” by the duality.

Concretely, the duality explains why the thermoelectric response of a strongly repulsive system shows features characteristic for attractive interaction. This is particularly visible in the characteristic energy scale of stationary linear transport of heat and charge, which is governed by a resonance occurring at an anomalous energy with unexpected thermal broadening. Both were shown to derive from the occupation number of a quantum dot with inverted Coulomb interaction. In addition, the fluctuations of this dual occupation number were shown to play a similarly important role for the linear heat conductance as the usual occupation fluctuations have for the charge conductance.

The technical advantage offered by the new duality relation is most obvious in the more complicated nonlinear regime. We provided very compact analytical formulas for all transport coefficients, namely the nonlinear thermopower, Peltier coefficient and Fourier heat, allowing for intuitive predictions and analyses of their characteristic features. Strikingly, in most cases, the duality allowed us to express the nonlinear thermoelectric properties in terms of equilibrium variables.

The definite advantages for the analysis and understanding of the thermoelectric response of an interacting single-level quantum dot are expected to extend also to more complex systems with, e.g., multiple levels and contacts. Indeed, the duality applies quite generally beyond the limitations [29] of the present paper, also to low-temperature, strongly-coupled quantum dot systems, which are of current interest [75,76,77] as there are still many interesting thermoelectric properties yet to be explored.