Packer Detection for Multi-Layer Executables Using Entropy Analysis
Abstract
:1. Introduction
1.1. Background
1.2. Multi-Layer Packing
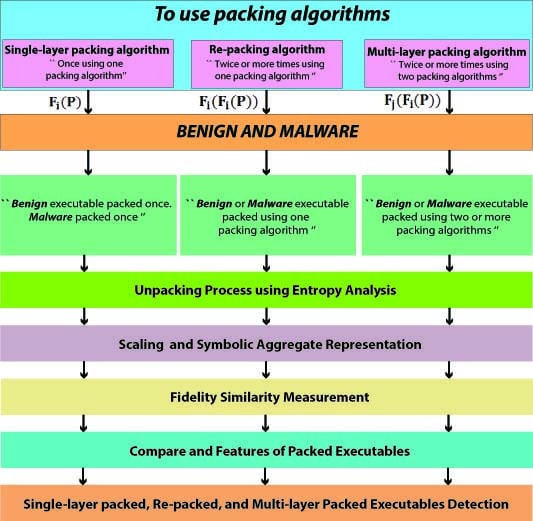
- Single-layer packing algorithm. A previous study of Bat-Erdene et al. [2] was devoted to single-layer packing algorithms.—Single-layer packed benign and malware executables; where is packer, P is benign or malware executable.
- Re-packing algorithm.—Re-packed benign and malware executables; where are same packers; P is benign or malware executable.
- Multi-layer packing algorithm.—Multi-layer packed benign and malware executables; where and are different packers; P is benign or malware executable.
1.3. Main Contributions
- We propose a method based on entropy analysis to detect executables re-packed or multi-layer packed two or more times.
- We develop a holistic method for identifying re-packer or multi-layer packer and determine their packing algorithms of given executables, irrespective of whether the re-packer or multi-layer packer of the executable are already known. This, to the best of our knowledge, is the first method to detect re-packer or multi-layer packer using machine learning. Considering experiment results, we claim that our approach is practically efficient and simpler than any other known methods.
- We introduce a data conversion method, which significantly reduces the space complexity by reducing data size by from 1/2 to 1/10000 times.
2. Related Work
3. Entropy Analysis for Detecting Single-Layer Packing, Re-Packing, or Multi-Layer Packing Algorithm
3.1. Packer Complexity Type
- Single-layer packing algorithm: These packers represent the simplest case. Single-layer packing uses only one packer to pack a given binary. This packing technique changes the size, number of sections and name of an executable (Figure 2).
- Re-packing algorithm: These packers contain re-packed unpacking layers, each one executed sequentially to unpack each of the sections. The re-packing algorithm uses the same packer two times to pack a given binary and utilizes compression techniques similar to those of a single-layer packer, but changes the size.
- Multi-layer packing algorithm: These packers contain multiple unpacking layers, each one executed sequentially to unpack the following routine. Once the original code has been reconstructed, the last transition transfers the control back to it. This packing uses a combination of potentially different packers to pack a given binary, and extensively facilitates the generation of a large number of packed binaries from the same input binary. Multi-layer packing algorithms change the size, number of sections and name of a single-layer packed executable.
3.2. Structure of Packer Detection Algorithm
3.3. Entropy Analysis and Measurement
| Algorithm 1: Unpacking packed executable. |
 |
3.4. Conversion into Symbolic Representation (SAX)
- Scale and normalize time-series;
| Algorithm 2: Conversion into SAX |
 |
4. Classifier
4.1. Fidelity Coefficient Similarity Measurement
4.2. Incremental Aggregate Analysis
5. Assessment of the Classification Method
Result of Experiments
- We depute packed benign notepad.exe from six packed benign executables.
- We extract entropy pattern of packed notepad.exe by 19 packing algorithms including the singe-layer packer, the re-packer, and the multi-layer packer.
- We scale entropy pattern of each packed notepad executable.
- We calculate the number of symbols for converting using SAX.
- New class includes MEW, Yoda’s Cryptor;
- Increasing class includes Alternate_EXE, NsPack, RLPack;
- Decreasing class consists of nPack;
- Combination class consists of VMProtect, Themida and Aspack;
- Constant class includes TELock.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Choi, H.; Zhu, B.B.; Lee, H. Detecting Malicious Web Links and Identifying Their Attack Types. In Proceedings of the 2nd USENIX Conference on Web Application Development, Portland, OR, USA, 15–16 June 2011; pp. 125–136.
- Bat-Erdene, M.; Kim, T.; Li, H.; Lee, H. Dynamic classification of packing algorithms for inspecting executables using entropy analysis. In Proceedings of the IEEE International Conference on Malicious and Unwanted Software: “The Americas” (MALWARE), Fajardo, PR, USA, 22–24 October 2013; pp. 19–26.
- Yan, W.; Zhang, Z.; Ansari, N. Revealing Packed Malware. IEEE Secur. Priv. 2008, 6, 65–69. [Google Scholar] [CrossRef]
- Wright, C.S. Packer Analysis Report Debugging and Unpacking the NsPack 3.4 and 3.7 Packer. Available online: https://www.sans.org/reading-room/whitepapers/malicious/packer-analysis-report-debugging-unpacking-nspack-34-37-packer-33428 (accessed on 14 March 2017).
- Guo, F.; Ferrie, P.; Chiueh, T.C. A study of the packer problem and its solutions. In Proceedings of the 11th International Symposium on Recent Advances in Intrusion Detection (RAID), Cambridge, MA, USA, 15–17 September 2008; pp. 98–115.
- Yara Rules Project. 2016. Available online: https://github.com/Yara-Rules/rules/ (accessed on 14 March 2017).
- GitHub. 2017. Available online: https://github.com/m-dwyer/packer-malware (accessed on 14 March 2017).
- Osaghae, E.O. Classifying Packed Programs as Malicious Software Detected. Int. J. Inf. Technol. Electr. Eng. 2016, 5, 22–25. [Google Scholar]
- Jacob, G.; Comparetti, P.M.; Neugschwandtner, M.; Kruegel, C.; Vigna, G. A static, packer-agnostic filter to detect similar malware samples. In Proceedings of the 9th International Conference on Detection of Intrusions and Malware, and Vulnerability Assessment (DIMVA), Heraklion, Greece, 26–27 July 2012; pp. 102–122.
- Brosch, T.; Morgenstern, M. Runtime Packers: The Hidden Problem; Black Hat: Washington, DC, USA, 2006. [Google Scholar]
- ASPack Software. Available online: http://www.aspack.com/aspack.html (accessed on 14 March 2017).
- Northfox’s Dungeon. MEW Software. Available online: http://northfox.uw.hu/index.php?lang=engid=dev (accessed on 14 March 2017).
- ASPack Software. Available online: http://www.aspack.com/asprotect32.html (accessed on 14 March 2017).
- NsPack 3.7. Available online: http://nspack.download-230-13103.programsbase.com/ (accessed on 14 March 2017).
- Oreans Technologies. Available online: http://www.oreans.com/themida.php (accessed on 14 March 2017).
- RLPack 1.2. Available online: http://rlpack.software.informer.com/1.2/ (accessed on 14 March 2017).
- VMPsoft. Available online: http://vmpsoft.com/products/vmprotect/ (accessed on 14 March 2017).
- Alternate_EXE Packer. Available online: http://www.alternate-tools.com/pages/c_exepacker.php?lang=ENG (accessed on 14 March 2017).
- Al-Anezi, M.M.K. Generic packing detection using several complexity analysis for accurate malware detection. Int. J. Adv. Comput. Sci. Appl. 2016. [Google Scholar] [CrossRef]
- Santos, I.; Ugarte-Pedrero, X.; Sanz, B.; Laorden, C.; Bringas, P.G. Collective classification for packed executable identification. In Proceedings of the 8th Annual Collaboration, Electronic Messaging, Anti-Abuse and Spam Conference, Perth, Australia, 1–2 September 2011; pp. 23–30.
- McAfee. The Good, the Bad, and the Unknown. Available online: http://www.techdata.com/mcafee/files/MCAFEE_wp_appcontrol-good-bad-unknown.pdf (accessed on 14 March 2017).
- Cesare, S.; Xiang, Y.; Zhou, W. Malwise—An effective and efficient classification system for packed and polymorphic malware. IEEE Trans. Comput. 2013, 62, 1193–1206. [Google Scholar] [CrossRef]
- Offensive Computing. Available online: http://www.offensivecomputing.net/ (accessed on 14 March 2017).
- VX Heavens. 2017. Available online: http://vxheaven.org/ (accessed on 14 March 2017).
- Ugarte-Pedrero, X.; Santos, I.; Sanz, B.; Laorden, C.; Bringas, P.G. Countering entropy measure attacks on packed software detection. In Proceedings of the 2012 IEEE Consumer Communications and Networking Conference (CCNC), Las Vegas, NV, USA, 14–17 Janaury 2012; pp. 164–168.
- Shafiq, M.Z.; Tabish, S.M.; Mirza, F.; Farooq, M. Pe-miner: Mining structural information to detect malicious executables in realtime. In Proceedings of the 12th International Symposium on Recent Advances in Intrusion Detection (RAID), Saint-Malo, France, 23–25 September 2009; pp. 121–141.
- Liu, L.; Ming, J.; Wang, Z.; Gao, D.; Jia, C. Denial-of-service attacks on host-based generic unpackers. In Proceedings of the International Conference on Information and Communications Security (ICICS), Beijing, China, 14–17 December 2009; pp. 241–253.
- Meijer, B.R. Rules and algorithms for the design of templates for template matching. In Proceedings of the 11th IAPR International Conference on Pattern Recognition, Conference A: Computer Vision and Applications, The Hague, The Netherlands, 30 August–3 September 1992; pp. 760–763.
- Cesare, S.; Xiang, Y. Classification of malware using structured control flow. In Proceedings of the Eighth Australasian Symposium on Parallel and Distributed Computing, Brisbane, Australia, 1 January 2010; pp. 61–70.
- Burges, C.J. A tutorial on support vector machines for pattern recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Martignoni, L.; Christodorescu, M.; Jha, S. Omniunpack: Fast, generic, and safe unpacking of malware. In Proceedings of the Computer Security Applications Conference (ACSAC), Miami Beach, FL, USA, 10–14 December 2007; pp. 431–441.
- Kang, M.G.; Poosankam, P.; Yin, H. Renovo: A hidden code extractor for packed executables. In Proceedings of the ACM Workshop on Recurring Malcode, Alexandria, VA, USA, 2 November 2007; pp. 46–53.
- Jeong, G.; Choo, E.; Lee, J.; Bat-Erdene, M.; Lee, H. Generic unpacking using entropy analysis. In Proceedings of the 2010 5th International Conference on Malicious and Unwanted Software (MALWARE), Nancy, France, 19–20 October 2010; pp. 98–105.
- Devi, D.; Nandi, S. Detection of packed malware. In Proceedings of the First International Conference on Security of Internet of Things, Kollam, India, 17–19 August 2012; pp. 22–26.
- Perdisci, R.; Lanzi, A.; Lee, W. Classification of packed executables for accurate computer virus detection. Pattern Recognit. Lett. 2008, 29, 1941–1946. [Google Scholar] [CrossRef]
- An in-Depth Look Into the Win32 Portable Executable File Format—Part 2. Available online: http://www.delphibasics.info/home/delphibasicsarticles/anin-depthlookintothewin32portableexecutablefileformat-part2 (accessed on 14 March 2017).
- Pietrek, M. Peering Inside the PE: A Tour of the Win32 Portable Executable File Format. Available online: https://msdn.microsoft.com/en-us/library/ms809762.aspx (accessed on 14 March 2017).
- Ugarte-Pedrero, X.; Balzarotti, D.; Santos, I.; Bringas, P.G. SoK: Deep packer inspection: A longitudinal study of the complexity of run-time packers. In Proceedings of the IEEE Symposium on Security and Privacy, San Jose, CA, USA, 17–21 May 2015; pp. 659–673.
- Lyda, R.; Hamrock, J. Using entropy analysis to find encrypted and packed malware. IEEE Secur. Priv. 2007, 5, 40–45. [Google Scholar] [CrossRef]
- Sun, L.; Versteeg, S.; Boztaş, S.; Yann, T. Pattern recognition techniques for the classification of malware packers. In Proceedings of the 15th Australasian conference on Information security and privacy, Sydney, Australia, 5–7 July 2010; pp. 370–390.
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Vapnik, V.; Chervonenkis, A.Y. Theory of Pattern Recognition: Statistical Problems of Learning; Nauka: Moscow, Russia, 1974. [Google Scholar]
- Lin, J.; Keogh, E.; Lonardi, S.; Chiu, B. A symbolic representation of time series, with implications for streaming algorithms. In Proceedings of the 8th ACM SIGMOD Workshop on Research Issues in Data Mining and Knowledge Discovery, San Diego, CA, USA, 13 June 2003; pp. 2–11.
- Keogh, E.; Kasetty, S. On the need for time series data mining benchmarks: A survey and empirical demonstration. Data Min. Knowl. Discov. 2003, 7, 349–371. [Google Scholar] [CrossRef]
- Keogh, E.; Chakrabarti, K.; Pazzani, M.; Mehrotra, S. Dimensionality reduction for fast similarity search in large time series databases. Knowl. Inf. Syst. 2001, 3, 263–286. [Google Scholar] [CrossRef]
- Yi, B.K.; Faloutsos, C. Fast time sequence indexing for arbitrary Lp norms. In Proceedings of the 26th International Conference on Very Large Data Bases (VLDB), Cairo, Egypt, 10–14 September 2000.
- Bat-Erdene, M.; Park, H.; Li, H.; Lee, H.; Choi, M.S. Entropy analysis to classify unknown packing algorithms for malware detection. Int. J. Inf. Secur. 2016. [Google Scholar] [CrossRef]









| a | |||||
|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 7 | |
| −0.43 | −0.67 | −0.84 | −0.97 | −1.07 | |
| 0.43 | 0 | −0.25 | −0.43 | −0.57 | |
| 0.67 | 0.25 | 0 | −0.18 | ||
| 0.84 | 0.43 | 0.18 | |||
| 0.97 | 0.57 | ||||
| 1.07 | |||||
| Variable | A Series Data |
|---|---|
| X | A time series |
| A PAA of a time series | |
| SAX of time series | |
| M | The number of PAA segments representing time series X, where M ≤ n |
| a | Alphabet size. a is integer, where a > 2 |
| Single-Layer Packer | Re-Packer | |
| Alternate_Exe | Alternate_Exe + Alternate_Exe | 0.9920 |
| nPack | nPack + nPack | 0.9908 |
| NsPack | NsPack + NsPack | 0.9982 |
| RLPack | RLPack + RLPack | 0.9914 |
| VMProtect | VMProtect + VMProtect | 0.9999 |
| Single-Layer Packer | Multi-Layer Packer | |
| Aspack | Section 1 | 0.9949 |
| NsPack | Section 0 | 0.9821 |
| NsPack | Section 1 | 0.9965 |
| VMProtect | Section 4 | 1.0000 |
| RLPack | Section 1 | 1.0000 |
| VMProtect | Section 3 | 1.0000 |
| VMProtect | Section 1 | 1.0000 |
| NsPack | Section 0 | 0.9961 |
| VMProtect | Section 1 | 1.0000 |
| RLPack | Section 0 | 0.9908 |
| 1. | 2. | 3. | 4. | 5. | 6. | 7. | 8. | 9. | 10. | 11. | 12. | 13. | 14. | 15. | 16. | 17. | 18. | 19. | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | FIRST PACKER | ||||||||||||||||||||
| PACKERS | Alternate_Exe | FSG | RLPack | NsPack | UPXN | UPX-iT | MPRESS | Morphine | nPack | Themida | VMProtect | Aspack | Molebox | Petite | ASProtect | MEW | Yoda’sCrypter | PELock | tELock | ||
| 1. | SECOND PACKER | Alternate_Exe v2.000 | Yes | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Yes | Failed | Failed |
| 2. | FSG v2.0 | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Yes | Failed | Yes | Failed | Failed | Failed | Yes | Failed | Failed | |
| 3. | RLPack v1.2 | Yes | Failed | Yes | Failed | Yes | Yes | Failed | Failed | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Failed | Yes | Yes | Yes | |
| 4. | NsPack v3.7 | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Failed | Failed | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Failed | Yes | Yes | |
| 5. | UPXN v301 | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | |
| 6. | UPX-iT v1.0 | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | |
| 7. | MPRESS v1.27 | Failed | Failed | Failed | Failed | Yes | Yes | Failed | Failed | Failed | Yes | Yes | Failed | Yes | Failed | Failed | Failed | Failed | Yes | Failed | |
| 8. | Morphine v1.6 | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | |
| 9. | nPack v1.1.300.2006 | Yes | Failed | Failed | Failed | Yes | Yes | Yes | Failed | Yes | Yes | Failed | Failed | Yes | Failed | Yes | Failed | Yes | Yes | Failed | |
| 10. | Themida v2.4 | Failed | Yes | Yes | Yes | Yes | Failed | Failed | Failed | Yes | Yes | Yes | Failed | Yes | Yes | Yes | Failed | Yes | Yes | Yes | |
| 11. | VMProtect v1.7 | Failed | Failed | Yes | Yes | Failed | Yes | Yes | Failed | Failed | Failed | Yes | Failed | Failed | Yes | Yes | Failed | Failed | Failed | Failed | |
| 12. | Aspack v2.28 | Yes | Failed | Failed | Yes | Yes | Yes | Yes | Failed | Yes | Failed | Yes | Yes | Yes | Yes | Yes | Failed | Yes | Yes | Failed | |
| 13. | Molebox v2.6.1 | Yes | Failed | Yes | Yes | Yes | Yes | Yes | Failed | Yes | Yes | Yes | Yes | Failed | Yes | Yes | Yes | Yes | Yes | Yes | |
| 14. | Petite v2.3 | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Yes | Failed | Failed | Failed | Failed | Failed | Yes | Yes | Failed | |
| 15. | ASProtect v.1.23 | Yes | Failed | Failed | Failed | Yes | Yes | Failed | Failed | Yes | Yes | Yes | Failed | Yes | Failed | Failed | Failed | Yes | Failed | Yes | |
| 16. | MEW v1.2 | Failed | Failed | Yes | Failed | Failed | Failed | Yes | Failed | Yes | Yes | Yes | Failed | Yes | Yes | Yes | Yes | Yes | Failed | ||
| 17. | Yoda’s Crypter v1.3 | Yes | Yes | Failed | Failed | Yes | Yes | Yes | Failed | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | |
| 18. | PELock v2.0 | Failed | Yes | Failed | Failed | Yes | Yes | Failed | Failed | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Failed | Yes | Failed | Yes | |
| 19. | tELock v0.98 | Failed | Failed | Failed | Failed | Yes | Yes | Failed | Failed | Yes | Yes | Yes | Failed | Yes | Yes | Failed | Yes | Yes | Yes | Failed | |
| 1. | 2. | 3. | 4. | 5. | 6. | 7. | 8. | 9. | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| N | FIRST PACKER | ||||||||||
| PACKERS | Alternate_Exe | RLPack | NsPack | nPack | Themida | VMProtect | Aspack | MEW | Yoda’sCrypter | ||
| 1. | SECOND PACKER | Alternate_Exe | Yes | Failed | Failed | Failed | Failed | Failed | Failed | Failed | Yes/not exe |
| 2. | RLPack | Yes | Yes | Failed | Yes | Yes/not exe | Yes | Yes | Failed | Yes | |
| 3. | NsPack | Yes | Yes | Yes | Failed | Yes/not exe | Yes | Yes | Yes | Failed | |
| 4. | nPack | Yes | Failed | Failed | Yes | Yes/not exe | Failed | Failed | Failed | Yes/not exe | |
| 5. | Themida | Failed | Yes | Yes | Yes/not exe | Yes | Yes/not exe | Failed | Failed | Yes/not exe | |
| 6. | VMProtect | Failed | Yes | Yes | Failed | Failed | Yes | Failed | Failed | Failed | |
| 7. | Aspack | Yes/not exe | Failed | Yes/not exe | Yes | Failed | Yes/not exe | Yes | Failed | Yes/not exe | |
| 8. | MEW | Failed | Yes | Failed | Yes | Yes | Yes | Failed | Yes | Yes/not exe | |
| 9. | Yoda’s Crypter | Yes/not exe | Failed | Failed | Yes/not exe | Yes/not exe | Yes/not exe | Yes/not exe | Yes/not exe | Yes/not exe | |
| Type of Packers | Operation | Name of Operation | Packers | |
|---|---|---|---|---|
| Section Number | Size | |||
| Single-layer packers | Equivalent | Increment | NESI | Themida |
| Decrement | NESD | - | ||
| Increment | Increment | NISI | nPack; VMProtect | |
| Decrement | NISD | - | ||
| Decrement | Increment | NDSI | Aspack; MEW; NsPack | |
| Decrement | NDSD | Alternate_Exe; RLPack | ||
| Re-packers | Equivalent | Increment | NESI | - |
| Decrement | NESD | - | ||
| Increment | Increment | NISI | Aspack + Apack; nPack + nPack | |
| RLPack + RLPack; Themida + Themida | ||||
| VMProtect + VMProtect | ||||
| Decrement | NISD | - | ||
| Decrement | Increment | NDSI | Nspack + Nspack | |
| Decrement | NDSD | Alternate_Exe + Alternate_Exe | ||
| Multi-layer packers | Equivalent | Increment | NESI | - |
| Decrement | NESD | Alternate_Exe + nPack | ||
| Increment | Increment | NISI | nPack + Aspack; NsPack + VMProtect | |
| RLPack + VMProtect | ||||
| Decrement | NISD | - | ||
| Decrement | Increment | NDSI | Alternate_Exe + NsPack; Aspack + NsPack | |
| Aspack + RLPack; Alternate_Exe + RLPack | ||||
| MEW + NsPack; nPack + MEW | ||||
| RLPack + MEW; nPack + RLPack | ||||
| RLPack + NsPack; Themida + MEW | ||||
| VMProtect + Aspack; VMProtect + MEW | ||||
| VMProtect + RLPack | ||||
| Decrement | NDSD | - | ||
| N | Packing Algorithm | ||||||
|---|---|---|---|---|---|---|---|
| Re-Packer | 1. | Alternate_EXE | 96.0 | 1.2 | 99.0 | 98.8 | 96.3 |
| 2. | ASPACK | 96.0 | 4.0 | 97.5 | 96.0 | 95.2 | |
| 3. | MEW | 100.0 | 0.0 | 100.0 | 100.0 | 100.0 | |
| 4. | NPACK | 100.0 | 0.8 | 98.4 | 99.2 | 100.0 | |
| 5. | NSPACK | 98.5 | 2.3 | 96.7 | 97.7 | 95.5 | |
| 6. | RLPACK | 95.8 | 4.2 | 97.0 | 95.8 | 90.8 | |
| 7. | THEMIDA | 96.0 | 1.9 | 99.0 | 98.1 | 92.3 | |
| 8. | VMPROTECT | 100.0 | 0.0 | 100.0 | 100.0 | 100.0 | |
| AVERAGE | 97.8 | 1.8 | 98.5 | 98.2 | 96.2 | ||
| N | PACKERS | ||||||
| Multi-Layer Packer | 1. | Alternate_EXE | 93.7 | 3.0 | 97.2 | 96.9 | 96.3 |
| 2. | ASPACK | 93.0 | 2.0 | 96.8 | 97.9 | 96.3 | |
| 3. | MEW | 94.5 | 1.3 | 98.8 | 98.6 | 98.0 | |
| 4. | NPACK | 95.0 | 5.5 | 97.3 | 94.5 | 96.8 | |
| 5. | NSPACK | 98.5 | 2.3 | 95.9 | 97.7 | 94.8 | |
| 6. | RLPACK | 93.0 | 3.5 | 95.8 | 96.4 | 95.8 | |
| 7. | THEMIDA | 96.0 | 0.5 | 98.1 | 99.5 | 96.7 | |
| 8. | VMPROTECT | 100.0 | 0.0 | 100.0 | 100.0 | 100.0 | |
| AVERAGE | 95.5 | 2.3 | 97.5 | 97.7 | 96.8 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bat-Erdene, M.; Kim, T.; Park, H.; Lee, H. Packer Detection for Multi-Layer Executables Using Entropy Analysis. Entropy 2017, 19, 125. https://doi.org/10.3390/e19030125
Bat-Erdene M, Kim T, Park H, Lee H. Packer Detection for Multi-Layer Executables Using Entropy Analysis. Entropy. 2017; 19(3):125. https://doi.org/10.3390/e19030125
Chicago/Turabian StyleBat-Erdene, Munkhbayar, Taebeom Kim, Hyundo Park, and Heejo Lee. 2017. "Packer Detection for Multi-Layer Executables Using Entropy Analysis" Entropy 19, no. 3: 125. https://doi.org/10.3390/e19030125
APA StyleBat-Erdene, M., Kim, T., Park, H., & Lee, H. (2017). Packer Detection for Multi-Layer Executables Using Entropy Analysis. Entropy, 19(3), 125. https://doi.org/10.3390/e19030125