Abstract
The classical secret-key agreement (SKA) scheme includes three phases: (a) advantage distillation (AD), (b) reconciliation, and (c) privacy amplification. Define the transmission rate as the ratio between the number of raw key bits obtained by the AD phase and the number of transmitted bits in the AD. The unidirectional SKA, whose transmission rate is , can be realized by using the original two-way wiretap channel as the AD phase. In this paper, we establish an efficient bidirectional SKA whose transmission rate is nearly 1 by modifying the two-way wiretap channel and using the modified two-way wiretap channel as the AD phase. The bidirectional SKA can be extended to multiple rounds of SKA with the same performance and transmission rate. For multiple rounds of bidirectional SKA, we have provided the bit error rate performance of the main channel and eavesdropper’s channel and the secret-key capacity. It is shown that the bit error rate (BER) of the main channel was lower than the eavesdropper’s channel and we prove that the transmission rate was nearly 1 when the number of rounds was large. Moreover, the secret-key capacity was from to as the error probability of channel was from to in binary symmetric channel (BSC). The secret-key capacity was close to as the signal-to-noise ratio increased in the additive white Gaussian noise (AWGN) channel.
1. Introduction
The one-time pad was developed by Vernam [1], by which a group of users can communicate messages among themselves securely if they share a common secret key beforehand. However, the key rate should be at least the message rate [2], and so the problem of secure communication effectively turns into the problem of secret-key agreement (SKA). In the SKA problem, legitimate users Alice and Bob aim at agreeing on a sequence of bits (key) that must be kept secret from the passive eavesdropper Eve. As shown in Figure 1, the classical SKA scheme includes three phases: (a) advantage distillation (AD), (b) reconciliation, and (c) privacy amplification [3]. AD aims to provide the legitimate agents an advantage over the eavesdropper. Information reconciliation aims at generating an identical random sequence at both Alice and Bob. Privacy amplification is the step that extracts a secret key from the identical random sequence agreed upon by the legitimate agents [4].
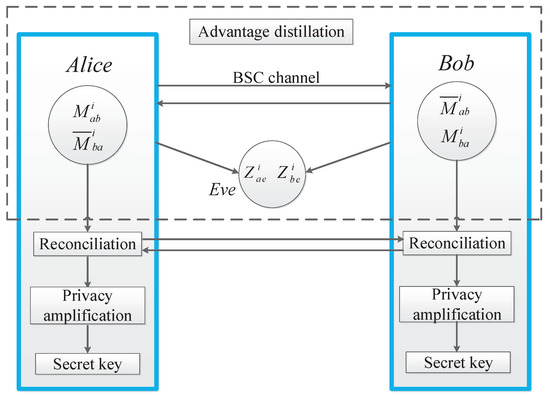
Figure 1.
Block diagram of the secret key agreement (SKA) scheme.
Bounds for the secret-key capacity have been derived for a large variety of communication channels [5,6,7,8,9]. Unfortunately, most do not provide direct insight into the design of practical secret-key capacity-achieving schemes. SKA based on noisy channels was presented in [5,10] using an additional insecure but authenticated public channel in which a third party can eavesdrop the communication but cannot forge it. This approach was recently extended in [11] to the model where the players share correlated Gaussian sources. In [12], opportunistic transmission was proposed for SKA over the quasi-static fading channel by sending signals only when the channel condition for the two legitimate players is better than the one for an adversary. The use of the reciprocity of wireless channels has been studied in [13,14,15] to study the key agreement. In [16], the SKA with public discussion was studied based on Gaussian and fading channels.
It is well known that Wyner [17] introduced the wiretap channel, in which a sequence M is transmitted from Alice to Bob over the main channel, while Eve is wiretapping over the eavesdropper’s channel. Wyner proved that Alice could send M to Bob in almost perfect secrecy if the main channel between Alice and Bob is better than Eve’s eavesdropper channel. Nevertheless, the assumption that the main channel is better (lower error rate) than the eavesdropper’s channel is generally impractical. This problem can be solved by using a two-way communication (TWC) as the main channel [18]. By using TWC, the message received by Eve over the eavesdropper’s channel is noisier than the message received by Bob. Therefore, the TWC scheme can be used as an AD scheme. Obviously, if we combine this AD scheme with any reconciliation and privacy amplification steps, the result can be used as secret keys between Alice and Bob [19]. However, the SKA of [18] is unidirectional from Alice to Bob, and therefore the transmission rate of this SKA is slow.
In this paper, emphasis is placed on the AD over the binary symmetric channel (BSC) and additive white Gaussian noise (AWGN) channel. We present a novel approach in building the two-way wiretap channel (TWWC) for bidirectional SKA. Different from all previous works, we will modify the original TWC scheme to be a bidirectional AD scheme to increase the transmission rate of the SKA and study the proposed AD over BSC and AWGN channel. We calculate the secret-key capacity of the proposed AD scheme to measure how many secret key bits can be shared between Alice and Bob. The advantages of the proposed bidirectional AD scheme are as follows.
- The proposed AD scheme provides an advantage of Alice and Bob over Eve when the channel between Alice and Bob is not less noisy than Eve’s eavesdropper channel.
- The unidirectional SKA—whose transmission rate is 0.5—can be realized by using the original TWWC as the AD scheme. However, a bidirectional SKA whose transmission rate is 1 can be realized by using the proposed AD scheme.
The remainder of this paper is organized as follows. Section 2 presents a general two-way wiretap channel; A single round of the SKA with the proposed AD scheme is introduced in Section 3; The proposed AD scheme is extended to multiple rounds and is introduced in Section 4; Section 5 proposes a bidirectional secret-key agreement over AWGN channel; Section 6 shows performances of the proposed systems; Finally, conclusions are drawn in Section 7.
2. Original Two-Way Wiretap Channel
2.1. Transmission Scheme
A TWWC between Alice and Bob was described in [18], in which the channel from Alice to Bob was considered to be error-free due to the powerful Low Density Parity Check (LDPC) codes. In this paper, we consider an original TWWC model shown in Figure 2, in which both main channel and eavesdropper channel are not error free.

Figure 2.
Advantage Distillation Scheme based on the original two-way wiretap channel.
The notations used throughout this paper are given in Table 1. In the conventional TWWC, to initiate a secure communication, Bob first transmits a random sequence Q to Alice. For , the raw keys are and , the error vectors of the main channel and the eavesdropper’s channel are , , , and . denotes the error vector of the main channel and denotes the error vector of the eavesdropper’s channel. The superscript 0 represents the process where Bob sends a random sequence Q to Alice and i represents that a raw key M is transmitted in the i-th round. The subscripts , and , denote sequences transmitted from Alice to Bob, from Bob to Alice and sequences wiretapped from Alice to Eve, and from Bob to Eve. We assume that the length of each sequence is n, so that the received sequences of Alice and Eve are
respectively, where the binary operator ⊕ denotes exclusive OR (XOR) operation [20]. Then, Alice uses the received sequence to calculate

Table 1.
Symbols.
Alice transmits to Bob through the main channel and Eve may wiretap this through the eavesdropper’s channel. Bob and Eve can receive the noisy version of , respectively, as
Since Bob knows the random sequence Q, he can XOR Q to U as
Eve only knows , which is the noisy version of Q, and she can only XOR to as
As shown in Figure 3, the raw key M is transmitted unidirectionally from Alice to Bob in the original TWWC. By comparing and , Eve has one more noisy term than Bob. Therefore, as long as the main channel is not worse than the passive eavesdropper’s channel (the weight of is not higher than that of and ), it is guaranteed that Eve is unable to arrive at the same sequence as Alice and Bob. Alice and Bob can use any reconciliation scheme and privacy amplification function to transform the raw key and into a much shorter secret key. Because of her errors, Eve is unable to predict Alice’s or Bob’s output of the privacy amplification. Finally, the secret key would be used as a one-time pad to ensure information-theoretic security between Alice and Bob. Furthermore, it is easy to see that this SKA is unidirectional from Alice to Bob. If Bob wants to send raw keys to Alice, they need another secure transmission with their roles exchanged.
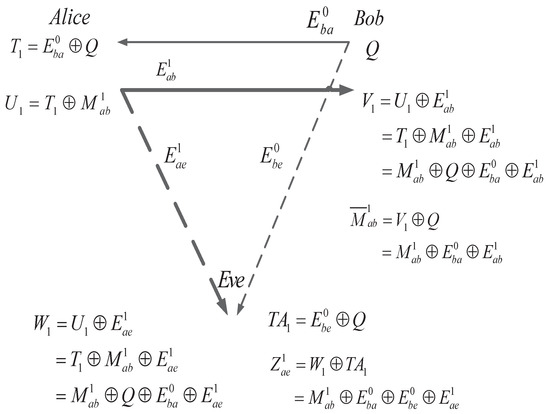
Figure 3.
Original two-way wiretap channel.
2.2. Transmission Rate
Following the literature [3], we denote as the transmission rate of the AD scheme. Let be the number of raw keys, and be the number of random sequences. Then, the transmission rate is calculated as
Following the definition, the transmission rate of the original unidirectional TWC scheme is
3. Bidirectional Secret-Key Agreement
If we use the above TWWC for AD in SKA, the raw keys are unidirectionally transmitted from Alice to Bob and the transmission rate is just . In order to increase the transmission rate of the SKA, we modify the original unidirectional TWWC to a bidirectional TWWC for the AD step of the SKA between Alice and Bob.
3.1. Proposed Advantage Distillation scheme
Assuming that there are l rounds of SKA between Alice and Bob, the first round of the proposed bidirectional AD scheme is as follows.
3.1.1. Preprocessing
Bob sends a random sequence Q, to Alice. The received sequences by Alice and Eve, respectively, are
where and , .
3.1.2. SKA from Alice to Bob
- (A1. 1)
- Alice uses the received sequence to calculatewhere . Alice sends over the main channel and Eve wiretaps through the eavesdropper’s channel.
- (A1. 2)
- Bob and Eve receive the noisy version of as and , respectively, as
- (A1. 3)
- Bob knows Q, so he can XOR Q to aswhere is the received raw key. Eve only knows the noisy version of Q, which is . Therefore, she can only XOR to aswhere in the eavesdropped raw key.
3.1.3. SKA from Bob to Alice
- (B1. 1)
- Before Bob sends the raw key to Alice, he has to makeThen, we can calculateand send to Alice through the main channel when Eve wiretaps it via the eavesdropper’s channel.
- (B1. 2)
- In this step, when Bob transmits the sequence to Alice, the noise of the two channels are and , respectively. Both Alice and Eve receive a noisy version of as and :
- (B1. 3)
- Alice has the knowledge of and Eve has the knowledge of , therefore Alice can obtain the intended raw key byand Eve can obtain the intended sequence by
Step A1 and Step B1 correspond to the first round of our proposed bidirectional AD scheme for SKA, which is shown in Figure 4. Note that Steps A1.1–A1.3 provide raw keys and ; we can do the reconciliation to correct errors between and and do the privacy amplification to get the secret keys shared between Alice and Bob. Similarly, Steps B1.1–B1.3 provide raw keys and , based on which we can also do the reconciliation and privacy amplification steps and obtain secret keys between Alice and Bob.
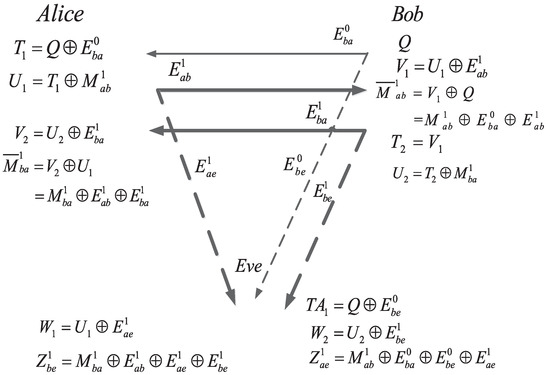
Figure 4.
First round of bidirectional secret-key agreement.
Let us define as the number of the raw keys, as the number of the random sequence Q. Then, the transmission rate of the proposed bidirectional AD over i round is
For example, for , and equals to and , respectively. However, for a large number of rounds, such as , almost equals to 1. Now, let us analyze the error probability of the main and eavesdropper’s channels in the following theorem.
Theorem 1.
Let the error probability of and be denoted as and the error probability of and be denoted as . After a round of the bidirectional TWC, the bit error probability of the main channel is , and the bit error probability of the eavesdropper’s channel is .
Proof.
Since Bob receives and the raw key is , the bit error probability of raw key is
Since Eve only has , her bit error probability is
☐
Let and , , and denote the capacity of the main channel and eavesdropper’s channel, bit error probability of main channel and eavesdropper’s channel, respectively. Assuming , the BER of the main channel and the eavesdropper’s channel are summarized in Table 2. We can also receive the secret-key capacity ,
where is the binary entropy function. Assuming , . Then, we can obtain

Table 2.
Bit error rate (BER) of main channel and the eavesdropper’s channel.
For the varying and , the corresponding , and are summarized in Table 3.

Table 3.
Channel capacity and secret-key capacity.
4. Multiple Rounds of Secret-Key Agreement
Assume that there are l rounds of SKA. Then, the ith round of bidirectional AD (shown in Figure 5) is as follows.
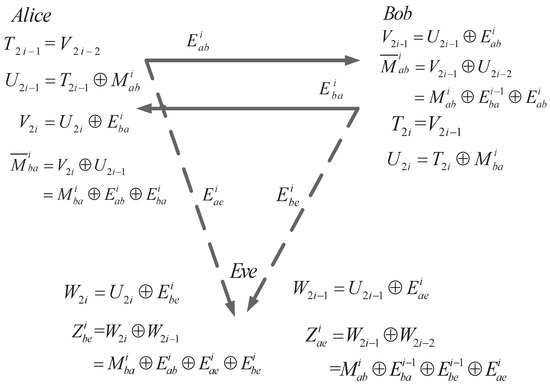
Figure 5.
The i-th round of bidirectional secret-key agreement.
4.1. SKA from Alice to Bob
- (A2. 1)
- LetThen, Alice sends the raw key to Bob by
- (A2. 2)
- Bob and Eve can receive the noisy version of as
- (A2. 3)
- Bob and Eve have the knowledge of and . Therefore, they can obtain the noisy version of by XOR and to and , respectively. The result is calculated asand
4.2. SKA from Bob to Alice
- (B2. 1)
- In the i-th round, Bob has to makeThen, he sends the raw key in the noisy form, which isover the main channel. Meanwhile, Eve may wiretap it by the eavesdropper’s channel.
- (B2. 2)
- Alice can receive , consisting of the noisy vector and , and Eve can receive , which consists of the noisy vector and ,
- (B2. 3)
- Alice and Eve have the knowledge of and , respectively. Therefore, they can obtain the noisy version of by XOR and to (36) and (37). The and can be received byand
As shown in Figure 6, the secret sequence M is transmitted bidirectionally between Alice and Bob in our proposed scheme. The BER of the main channel and eavesdropper’s channel in the i-th round is the same as that of the first round. Transmission rate after l rounds of the proposed AD is
which is close to 1 when l is large enough.

Figure 6.
Proposed bidirectional advantage distillation scheme.
5. Bidirectional Secret-Key Agreement over AWGN Channel
Now, let us demonstrate the proposed AD scheme over the AWGN channel. Assume that there are l rounds of SKA over AWGN channel as well. Then, the i-th round shown in Figure 7 is as follows.
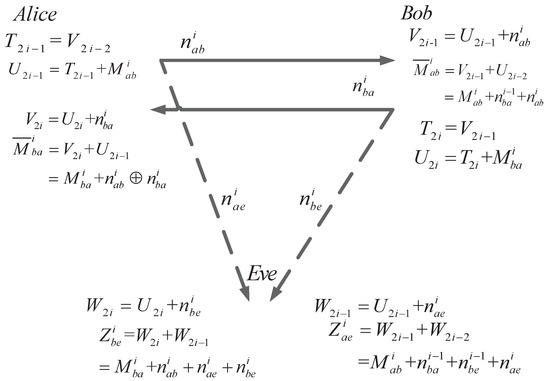
Figure 7.
The i-th round of bidirectional secret-key agreement over AWGN channel.
5.1. SKA from Alice to Bob
- (A3. 1)
- LetThen, Alice sends the raw key to Bob bywhere (, , ⋯, )
- (A3. 2)
- Bob and Eve can receive the noisy version of aswhere the variance of AWGN over the main channel and the eavesdropper’s channel are and , respectively.
- (A3. 3)
- Bob and Eve can obtain the noisy version of by minusing and to and , respectively. The result will beandwhere the variance of AWGN or is .
5.2. SKA from Bob to Alice
- (B3. 1)
- In the ith round, Bob has to makeThen, he sends the raw key in the noisy form, which isover the main channel.
- (B3. 2)
- Alice can receive , consisting of the noisy vector and , and Eve can receive , which consists of the noisy vector and ,
- (B3. 3)
- Alice and Eve can obtain the noisy version of by minusing and to (48) and (49). and can be received byand
Now, let us calculate the capacity of the main channel and the eavesdropper’s channel by and . Because the variance of the main channel and the eavesdropper’s channel are and , we can calculate
and
We can also receive the secret-key capacity over it.
6. Performance Analysis
In this section, we evaluate performance of the proposed AD scheme over BSC channel in terms of BER and and performance of the proposed AD scheme over AWGN channel . The length n of raw key is 10,000. BER simulation results are shown in Figure 8. With the increasing crossover probability p, the BER increases as well. This indicates that performance of the main channel between Alice and Bob is superior to that of the eavesdropper’s channel under the same number l of rounds and length n of the secret sequence.
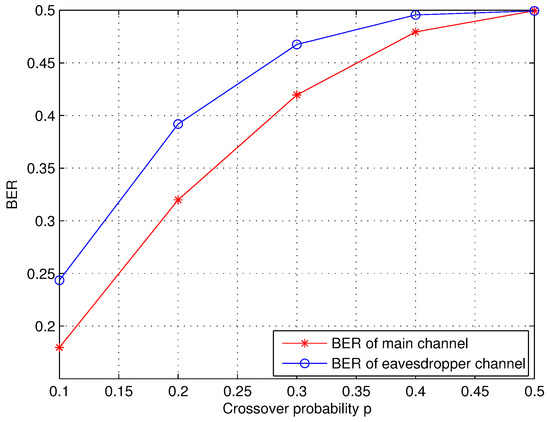
Figure 8.
The BER performance of the main channel and eavesdropper’s channel over binary symmetric channel (BSC).
We also show the capacity of main channel, eavesdropper’s channel, and the difference between them that is secret-key capacity over BSC channel in Figure 9 and over AWGN channel in Figure 10. Assuming that , the secret-key capacity increases as and increase. However, when , the secret-key capacity decreases with the increase of and . In the AWGN channel, the is close to when the signal-to-noise ratio (SNR) is from 0 to 50.
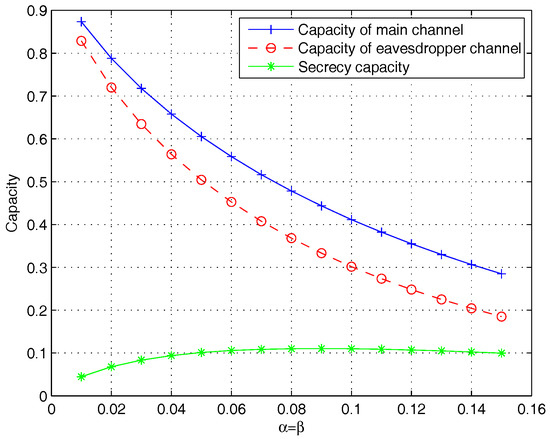
Figure 9.
The secret-key capacity and capacities of the main channel and eavesdropper’s channel over BSC channel.
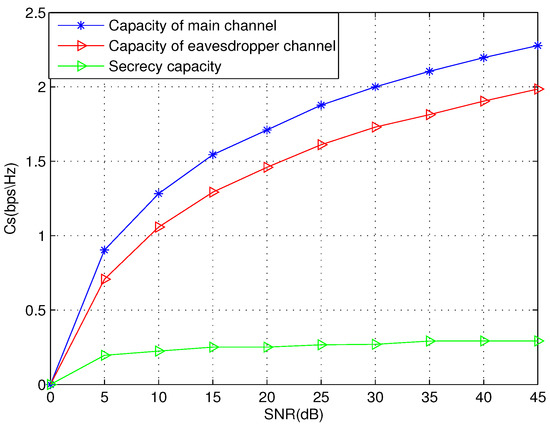
Figure 10.
The secret-key capacity and capacities over additive white Gaussian noise (AWGN) channel.
Comparing to the AD schemes using the original two-way wiretap channel, the advantage of our scheme is that we need fewer rounds of communication between Alice and Bob to obtain the same amount of keys. Furthermore, since we need fewer rounds of communication, we also need less XOR operations to obtain the same amount of keys. In each round of the unidirectional AD scheme, using the original two-way wiretap channel, Alice and Bob need 1 XOR operation, respectively, in (3) and (6). In each round of the proposed bidirectional AD scheme, Alice needs 2 operations in (12) and (21), and Bob needs 2 operations in (15) and (18). Therefore, in each round of the proposed bidirectional AD scheme, the number of XOR operations is two times higher than that in the unidirectional AD scheme. However, our bidirectional scheme also has a transmission rate of secret keys which is two times greater than that of the unidirectional AD scheme. Therefore, our scheme needs the same number of XOR operations to obtain the same amount of secret keys as the unidirectional AD scheme. We have listed the transmission rate, XOR operations of the unidirectional AD scheme and the proposed bidirectional AD in Table 4.

Table 4.
Transmission rate number of XOR operations of different schemes with l rounds, l is large enough. TWWC: two-way wiretap channel.
7. Conclusions
In this paper, we modified the original unidirectional TWWC to a bidirectional TWWC for the AD step of the SKA between Alice and Bob over BSC channel and AWGN channel. The proposed bidirectional secret-key agreement can be used to distribute keys between Alice and Bob and its transmission rate is better than the secret-key agreement of unidirectional TWWC. The BER and capacity were calculated first, and then we evaluated the performance of the proposed AD scheme in terms of BER over BSC channel and secret-key capacity over both channels. The BER of the main channel is lower than the eavesdropper’s channel, and analysis of the transmission rate is nearly 1 when the number of rounds is large. Moreover, The secret-key capacity is from to as the error probability of channel is from to in the BSC channel. In the AWGN channel, the secret-key capacity is close to as the SNR increases.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (61671143,61571315,61631004), Shanghai Rising-Star Program (15QA1400100), Key Accident Prevention Technology Project for State Administration of Work Safety (zhishu-0016-2017AQ) and Langfang Research and Development Program about Science & Technology (2016011034).
Author Contributions
Xue-Qin Jiang proposed the new AD scheme; Hui-Ming Wang analyzed the secret-key capacity; Jia hou designed all the simulations; Yi Yang performed the simulations; Yan Feng wrote the paper. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Vernam, G.S. Cipher printing telegraph systems for secret wire and radio telegraphic communications. Trans. Am. Inst. Electr. Eng. 1926, 45, 295–301. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Tomasin, S. Secret key agreement by LLR thresholding and syndrome feedback over awgn channel. IEEE Commun. Lett. 2014, 18, 26–29. [Google Scholar] [CrossRef]
- Cao, Y.; Jiang, X.Q.; Wang, H.M.; Bai, E.; Li, J. Advantage distillation over MIMO wiretap channels based on generalized extended orthogonal space-time block codes. In Proceedings of the 2016 International Conference on Computer, Information and Telecommunication Systems (CITS), Kunming, China, 6–8 July 2016; pp. 1–5. [Google Scholar]
- Maurer, U. Secret key agreement by public discussion from common information. IEEE Trans. Inf. Theory 1993, 39, 733–742. [Google Scholar] [CrossRef]
- Csiszar, I.; Narayan, P. Common randomness and secret key generation with a helper. IEEE Trans. Inf. Theory 2000, 46, 344–366. [Google Scholar] [CrossRef]
- Csiszar, I.; Narayan, P. Secrecy capacities for multiterminal channel Models. IEEE Trans. Inf. Theory 2008, 54, 2437–2452. [Google Scholar] [CrossRef]
- Watanabe, S.; Oohama, Y. Secret key agreement from vector Gaussian sources by rate limited public communication. Proc. IEEE Int. Symp. Inf. Theory 2010, 93, 2597–2601. [Google Scholar]
- Nitinawarat, S.; Narayan, P. Secret key generation for correlated Gaussian sources. IEEE Trans. Inf. Theory 2012, 58, 3373–3391. [Google Scholar] [CrossRef]
- Ahlswede, R.; Csiszar, I. Common randomness in information theory and cryptography-Part I: Secret sharing. IEEE Trans. Inf. Theory 1993, 39, 1121–1132. [Google Scholar] [CrossRef]
- Naito, M.; Watanabe, S.; Matsumoto, R.; Uyematsu, T. Secret key agreement by soft-decision of signals in Gaussian Maurer’s model. IEICE Trans. Fundam. 2009, 92, 525–534. [Google Scholar] [CrossRef]
- Bloch, M.; Barros, J.; Rodriguez, M.R.D.; McLaughlin, S.W. Wireless information-theoretic security. IEEE Trans. Inf. Theory 2008, 54, 2515–2534. [Google Scholar] [CrossRef]
- Kobara, K.; Morozov, K.; Imai, H. On the possibility of key agreement using variable directional antenna. In Proceedings of the 1st Joint Workshop on Information Security, Seoul, Korea, 20–21 September 2006; pp. 1432–1436. [Google Scholar]
- Aono, T.; Higuchi, K.; Ohira, T.; Komiyama, B.; Sasaoka, H. Wireless secret key generation exploiting reactance-domain scalar response of multipath fading channels. IEEE Trans. Antennas Propag. 2005, 53, 3776–3784. [Google Scholar] [CrossRef]
- Ye, C.; Mathur, S.; Reznik, A.; Shah, Y.; Trappe, W.; Mandayam, N.B. Information-theoretically secret key generation for fading wireless channels. IEEE Trans. Inf. Forensics Secur. 2010, 5, 240–254. [Google Scholar]
- Isaka, M.; Kawata, S. Signal sets for secret key agreement with public discussion based on Gaussian and fading channels. IEEE Trans. Inf. Forensics Secur. 2011, 6, 523–531. [Google Scholar] [CrossRef]
- Wyner, A.D. The wire-tap channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Wen, H.; Gong, G.; Ho, P.H. Build-in wiretap channel I with feedback and LDPC codes. J. Commun. Netw. 2009, 11, 538–643. [Google Scholar] [CrossRef]
- Bloch, M.; Barros, J. Physical-Layer Security: From Information Theory to Security Engineering; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Pacher, C.; Grabenweger, P.; Martinez-Mateo, J.; Martin, V. An information reconciliation protocol for secret-key agreement with small leakage. In Proceedings of the 2015 IEEE International Symposium on Information Theory (ISIT), Hong Kong, China, 14–19 June 2015; pp. 730–734. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).