Paths of Cultural Systems

Abstract

A theory of cultural structures predicts the objects observed by anthropologists. We here define those which use kinship relationships to define systems. A finite structure we call a partially defined quasigroup (or pdq, as stated by Definition 1 below) on a dictionary (called a natural language) allows prediction of certain anthropological descriptions, using homomorphisms of pdqs onto finite groups. A viable history (defined using pdqs) states how an individual in a population following such history may perform culturally allowed associations, which allows a viable history to continue to survive. The vector states on sets of viable histories identify demographic observables on descent sequences. Paths of vector states on sets of viable histories may determine which histories can exist empirically.

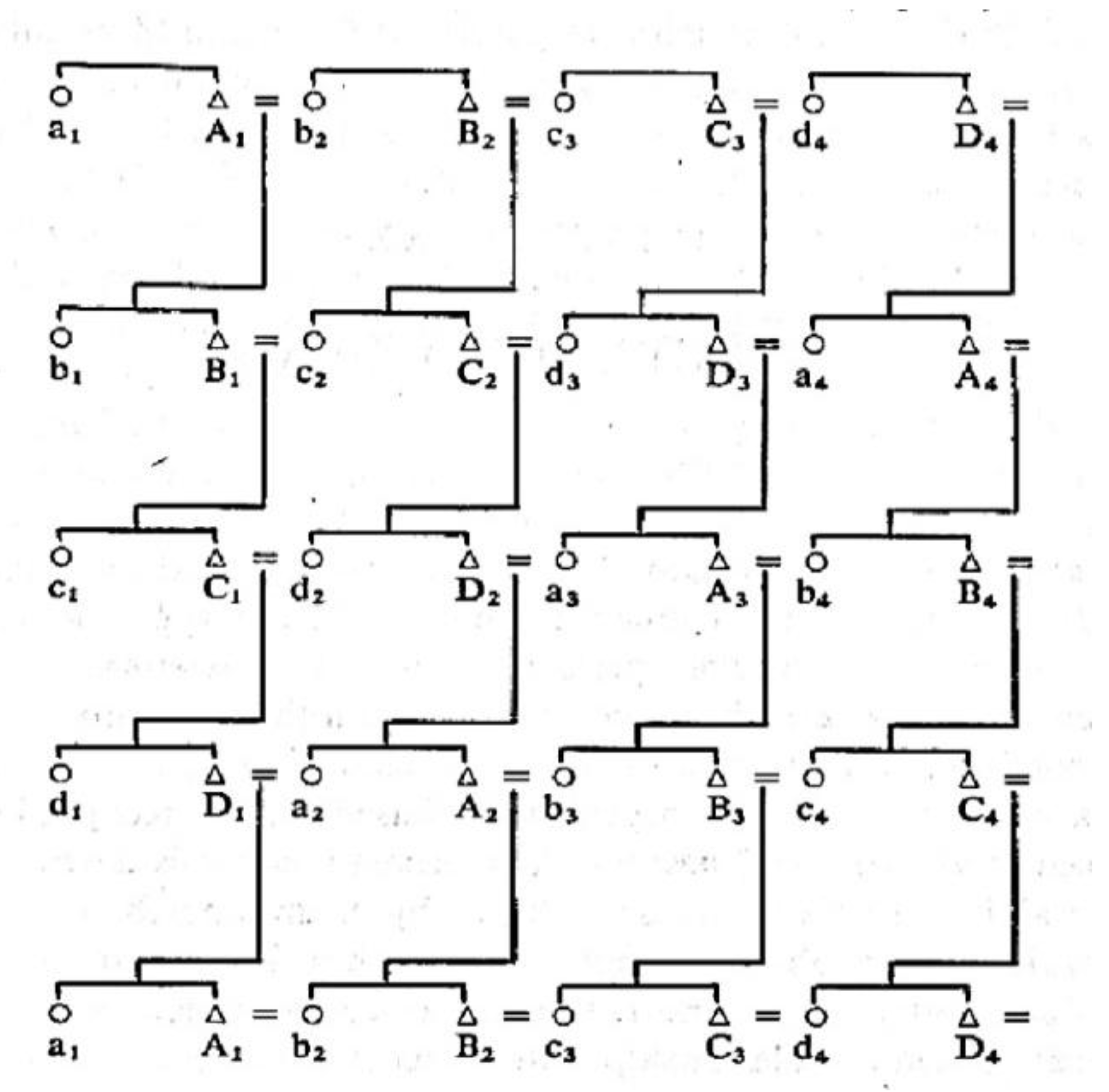
1. Ethnographic Foundation

The structures described here and their consequences imply much of what may be predicted about empirical cultures. Anthropologists very often draw illustrations of structures using methods discussed here, but based on intuition, thus have little notion of what their commonly used diagrams might predict. While [1,2] defined mathematical means to describe the current and future demographic organization of lineage organizations, with empirical examples, we here specify the demography of kinship-based systems [3,4,5,6,7,8] with some related definitions in our Appendix A; and empirical examples in [9,10,11,12,13]. We follow the inspiration of [14]. In an empirical culture many other relations may also occur; we note some of those in our Part 7, Discussion at the end.

Our notion of studying viable minimal structures—which are the smallest minimal cultural structures that can “reproduce” the ascribed social relations in one generation—follows from [15]. Our history describes how sustaining those relations allow the culture to reproduce the rules. Cultural rules describing histories may be stated in natural languages, which label the individuals in a descent sequence with a subset called a kinship terminology. Our term viable embodies what anthropologist Radcliff-Brown called “persistent cultural systems” ([10], p. 124). Radcliff-Brown and others often described histories using discrete generations, as do we. Empirical cultures are almost ubiquitously described by many anthropologists using viable histories, typically represented in an ethnography by its minimal structure. The nearly ubiquitous presence in ethnographies of viable histories implies they may be the only observed histories.

An example is Figure 1 (whose source is [9]) which is an actual viable minimal structure of a history (that is, a persistent cultural system). The triangles in the illustration are males, the circles are females, descent moves in the downward direction, the labels are names used in the kinship terminology. The sign “=” means “marriage” between the two individuals attached to it; the “=” on the far right in the illustration shows a marriage to the partner on the far left in each generation. The horizontal line which connects two individuals shows that those two are assigned descendants of the marriage above them. The fifth generation in this illustration is equal to the first (by its labels in vertical descent in the diagram), showing that minimal structure shown here reproduces the labelled culture here in four generations, but reproduces the minimal structure (the graphs without the kinship labels) in each generation. This minimal structure has 4 marriages in each generation hence has structural number s = 4. The minimal structure is not intended to illustrate the actual empirical relations of each empirical generation of individuals, instead it shows “how the rule operates”—it describes the minimal representation of the kinship and marriage rules (see Appendix A Definitions A3). The minimal structure describes the “principles” used in the rules of the culture.

Figure 1 is also obviously an example of a group. Claude Levi-Strauss [9] initially used groups to demonstrate histories in an appendix by A. Weil. Ref. [9] mainly discusses groups of orders 2, 4 and 8, though its illustration 1.17 shows a helical structure of order 4. Other studies include orders 3, 6 and others. Ref. [16] also shows a helical structure of order 7; helical minimal structures are also groups and have surjective descent sequences, so our modal demography discussed in [8] and Appendix A Definition A7 also apply to helices.

2. Basic Definitions

While lineage organizations [1,2] predicted examples of population measures including the “local” village size given the lineage structure, the kinship examples described here use values found in [8] to predict values associated to the structural number of the history, which apply no matter what the empirical size of the total population (so long as it is at or above the minimal size). Our definitions are stated in our Appendix A from previous articles (see also Appendix A) and those below.

Definition 1.

Let D be a finite non-empty set (called a dictionary) and let * be a partially defined binary operation on D, such that when x, y ∈ D:

(1) 

If there exists an a ∈ D such that a*x and a*y are defined and a*x = b and a*y = b then x = y, we call such object (D, *) a partially defined quasigroup, or pdq.

(2) 

If (D, *) is a pdq and * is fully defined on D, then (D, *) is a (complete) quasigroup.

(3) 

The pair L = (D, *) is a natural language with dictionary D whenever (D, *) is a pdq.

(4) 

If L = (D, *) is a natural language, a kinship terminology is a quasigroup subset k ⊆ L.

Definition 2.

Let X, Y and Z be non-empty finite sets and let (X, *), (Y, °) and (Z, ▪) be quasigroups with binary relations *, ° and ▪ respectively. Then:

(1) 

A function f: X → Y is a homomorphism if f for all b, c ∈ X, f(b * c) = f(b) ° f(c).

(2) 

If f: X → Z and g: Y → Z are homomorphisms then f and g are isotopic.

All empirical languages are natural languages [7]. Under Definition 2(2) if Y and Z are isotopic they are also istotopic dictionaries: two possibly different descriptions, thus typically of distinct natural languages, of the “same” objects or illustrations. Our definition of kinship terminologies based on quasigroups follows from [17], which refined the discussion of Weil in [9]. While empirical kinship systems are non-associative [18], a large class is associative and complete, form finite permutations, indeed groups [19,20,21] hence form kinship terminologies as defined here. Groups thus arise in anthropology because a set of all 1-1 mappings of a finite subset set k of a quasigroup (a kinship terminology k) onto itself forms a group (the symmetric group on k). If (X, *), (Y, °) and (Z, ▪) are complete pdqs then (isotopic) homomorphisms classify kinship terminologies by the form of the pdq onto which they are mapped. For example, the isotopic terminologies classified as Dravidian [12,22,23] and others are often discussed, in part because they have interesting group theoretical structures.

Definition 3.

Let H be a non-empty finite set of viable histories. Let G be a non-empty descent sequence using H, let G_t ∈ G be a generation of G at t, and let H_t ⊆ H be a subset of t. Then then for each α ∈ H_t, the real numbers 0 $\le$ v_α(t) $\le$ 1 such that Σ_αv_α(t) = 1 is the vector state of G_t.

Adopting a standard order for listing the histories, we write the vector state at t as v(t) := (v_α(t), …, v_χ(t)), or when |H_t| = h, as v(t) = (v₁(t), …, v_h(t)). Let H be a finite non-empty set of viable histories, let α ∈ H, let G_t ∈ G be a generation of G, and let v(t) be the vector state of G_t (see also Appendix A Definitions A2–A5). Then:

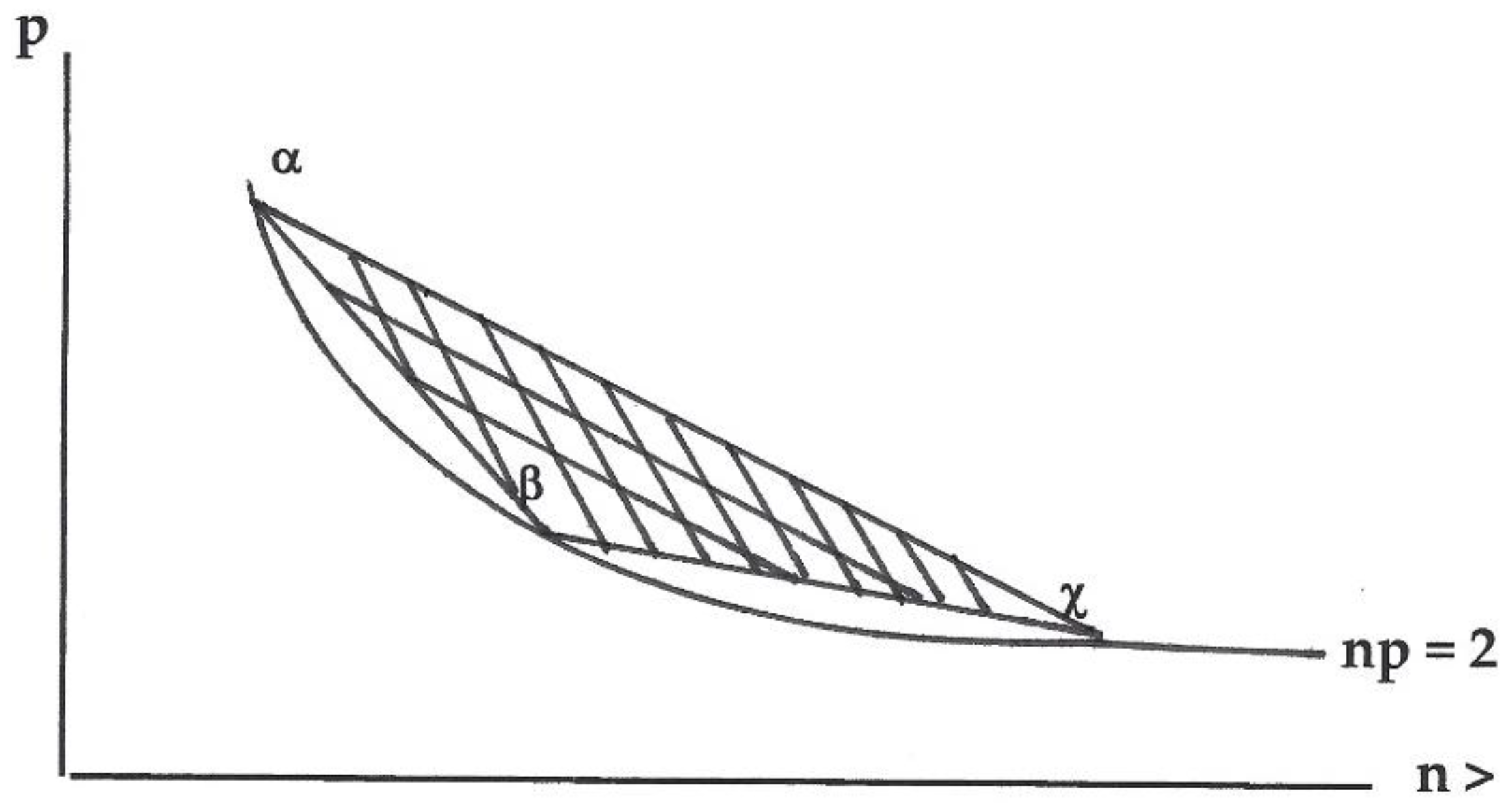
• From [2,5,6,8] and Appendix A Definition A4 each structural number s has a set of values n_s and p_s where n_sp_s = 2, where n_s is the average family size of a pure system of structural number s and p_s is the proportion of reproducing adults of a pure system of structural number s. If history α has structural number s, then each α has modal demography (n_α, p_α) = (n_s, p_s) (see Appendix A Definition A7) where p_s = 2/n_s; for s ≥ 3 and s_α ≠ s_χ then (n_α, p_α) ≠ (n_χ, p_χ).
• Determination of the (n_s, p_s) values are based on the Stirling Number of the Second Kind (SNSK) see [8,24]. We assume here the (n_s, p_s) pairs determined by [8].
• Since H is finite, each non-empty set of viable histories H thus has a largest structural number s_max with modal demography (n_max, p_max), and a smallest structural number s_min with modal demography (n_min, p_min). Note that if n_max increases then p_max decreases (and as n_min decreases then p_min increases, since given s, n_sp_s = 2, with 0 < p ≤ 1. Structural numbers s = 2 or 3 have identical modal demography (n_s, p_s) = (2, 1); all others structural numbers have distinct modal demographies see [5,8].
• The modal demography of history α with structural number s_α is (n_α, p_α) = (n_s, p_s) is a set of values that represent the history α maintaining its modal demography with neither increase nor decrease in total empirical population size; it is prediction of n_α and p_α based on the determination that the structural number is s, and maintains the structural number s.
• n(t) = Σ_αv_α(t)n_α, α ∈ H, is the predicted average family size of G_t at t, given the vector state at t see [8]. Note that this is the average family size of the population at time t, given the vector state of each α ∈ H_t. This while the “size” of the minimal structure might be small, the size predicted by n(t) is the predicted actual size of the total population at t, not of the minimal structure; the minimal structure illustration “size” is dependent on the rules, not on the empirical size of the population.
• p(t) = Σ_αv_α(t)p_α, α ∈ H, is the predicted proportion of reproducing adults of G_t at t ascribed as married and reproducing, given the vector state of s_α at t [8].
• Thus, all of the “demographics” of cultural theory discussed here are predictions on the result of maintaining or changing the vector states of t, given the SNSK determined values for each modal demography (n_α, p_α) at time t. Thus, [8] defines

  e^r(t) = 1/2n(t)p(t)

  (1)

  where r(t) ∈ R predicts an average rate of change of total population size between two generations of G, based on the vector state of structural numbers of the histories H_t ⊆ H. [8] showed that r(t) predicts changes in the probabilities v(t) imply cultural change is adiabatic.
• Let H be a finite non-empty set of viable histories, and α, χ ∈ H. Using v_α(t) = 1 − v_χ(t), n_α = 2/p_α and n_χ = 2/p_χ, then Equation (1) becomes

  e^r(t) = 1 + (n_αχ – 2)v_α(t) + (2 – n_αχ)v_α(t)²

  (2)

  where:

  n_αχ := (n_α² + n_χ²)/(n_αn_χ)

  (3)

  is a constant determined by the values of n_α and n_χ; note n_αχ = n_χα.

3. Paths of Descent Sequences

Definition 4.

Let H be a finite set of non-empty viable histories. Let α, χ, etc ∈ H_t ⊆ H and let the structural number of α ≠ χ, etc. If for any such set, |H_t| > 1, v_t(α) = 1 or 0, then H is not full; otherwise H is full.

Definition 5.

If H is a finite non-empty set of viable histories, then F ⊆ H is a face of H see [2,4,8]. Let I = [1, 0]. A path from point a to point b in a set X is a function f: I → X with f(0) = a and f(1) = b, in which case a is called the initial point of the path and b is called the terminal point of the path. Given a path, in case a = b then such path is a closed path. If [x, y] ∈ I and f(x) = a and f(y) = b then f[x, y] is called an interval and a sub-path of I. A reverse path from point a to point b in X is a function f: I → X with f(1) = a and f(0) = b. Given a path (or reverse path) from t₀ to t₁, if t₁ ≥ t_k ≥ t₀ we say that t_k is in the path.

Lemma 1.

Let H_t be a finite non-empty set of full viable histories and α, χ ∈ H_t. Then:

1. 

r(t) ≥ 0, and r(t) = 0 if all structural numbers have the same modal demography or if all have structural numbers 2 or 3.

2. 

If α and χ are distinct structural numbers and at least one has structural number >3, then r(t) > 0 and r(t) has a maximum at v(t) = (0.5, 0.5).

3. 

Given any finite non-empty set H of two or more viable histories, there is a unique maximum r(t), given by (ii).

Proof 1.

Assume first the modal demographies of histories α and χ are equal (which occurs if s_α = s_χ or if s_α, s_χ < 4). Then n_α = n_χ. Then n_αχ = 2, so the sum in Equation (2) is e^r(t) = 1, or r(t) = 0. Assume now s_α ≠ s_χ and at least one structural number is >3, so the modal demographies of α and χ are distinct, and we do not have v_α(t) = 0 or 1. Then in Equation (2) (n_αχ − 2) = −(2 − n_αχ), but v_α(t) > 0, so then v_α(t) > v_α(t)². Thus, (n_αχ − 2)v_α(t) > (2 − n_αχ)v_α(t)², so Equation (2) states r(t) > 0. ☐

Proof 2.

To show r(t) has a maximum when v(t) = (0.5, 0.5), we use the first two terms of a Taylor expansion from (1) to find e^r(t) = 1 + r(t). Differentiating twice gives a² exp[r(t)]/δy² = 2 − 2n_αχ where y = v(t). When s_α ≠ s_χ and at least one of s_α, s_χ is > 3, n_αχ > 2, then exp[r(t)] is concave down; so, r(t) is also concave down. ☐

Proof 3.

There is a finite number of two-history pairs in H. Since n_s increases as s increases, then Lemma 1 part 1 shows that the largest value of r(t) will be set by that two-history subset α, χ of H having the largest difference between their structural numbers, hence the largest n_αχ in Equation (3). Combining the n_s of the largest s with any other combination of n_s values will result in a smaller n_αχ hence smaller e^r(t), from Equation (3). ☐

Observation 1.

Assume a finite non-empty set of viable histories H acting on a finite non-empty descent sequence G. Let α, β, χ ∈ H_t ⊆ H act on generation Gt ∈ G. See Figure 2:

The curved bottom-line in Figure 2 is the locus wherever np = 2, so includes the modal demography of each history in H; that is, the modal demography for each of α, β and χ each appear on the line np = 2, since n_sp_s = 2. If for any α, v_α(t) = 1, then n(t) = n_α, p(t) = p_α, so e^r(t) = ½n(t)p(t) = ½n_αp_α = ½2 = 1 so r(t) = 0; this occurs if all histories in H_t have the same structural number (or all have structural numbers 2 and 3). When that does not occur we have a set of two or more histories in H_t each with 0 < v_α(t) < 1 and thus r(t) > 0; see also Lemma 1. When H is full, assume α, β and χ have distinct structural numbers, at least two of α, β, χ have structural numbers >3, and α is has the lowest structural number of those three histories. Then the modal demography of α, β, χ have (n_α, b_α) ≠ (n_β, b_β) ≠ (n_χ, b_χ), and the computation of r(t) appears in the values in the triangle area of Figure 2. However, if H_t is not full then events in the triangle area might not occur. Even if paths allow α with β, α with χ and β with χ (thus the boundaries of the triangle area), values of r(t) within the triangle only occur if all three histories are allowed by H, which may be prohibited by not-full H. We call such area an un-accessed region. Thus, we study change using both full and non-full sets of histories.

4. Pictures of States on Descent Sequences

Definition 6.

Let H be a finite non-empty set of histories and let (n_α, p_α) be the modal demography for history α ∈ H. Let G be a finite non-empty descent sequence using H, and let G_t ∈ G be the generation at time t. Let H_t be a face of H specified at t. Let S_t := { s_α|α ∈ H_i} be the set of structural numbers S_t ⊆ S of histories H_t available at t. Let A_t := {(n_α, p_α)|s_α ∈ S_i, α ∈ H_i, (n_α, p_α) = (n_s, p_s)} be the set of modal demographies A_t of the histories in H_t; and let v(t) be the vector state of G_t. List the histories in H in a defined order from α to χ. Then for all α ∈ H_t and all (n_α, p_α) ∈ A_t, let:

1. 

(n_t|:= (n_α, …, n_χ) be a row vector;

2. 

|p_t) := (p_α,…, …, p_χ) be a column vector;

3. 

for all α, χ∈ H, arranging the sum of the inner product (n_t|p_t) as a square matrix then for all α, χ∈ H, H(t): = [n_αp_χ] is a demographic picture (analogous to a Heisenberg picture in physics) at t;

4. 

the square matrix we get by arranging the products of v(t)v(t)^T as V(t) := [v_αχ(t)] is a probability picture (analogous to a Schroedinger picture in physics) of the vector state of a descent sequence at t;

5. 

for ε ≥ 0 let V(Δ(t)) := V(t + ε) − V(t) = [v_αχ(t + ε) − v_αχ(t)] := [Δ_αχ(t)]. (Notice that −1 ≤ Δ_αχ(t) ≤ 1).

We note [25] for our analogy of terminology.

Then for all α, χ ∈ H we can rewrite Equation (1) as:

e^r(t) = ½ (n|V(t)|p)

(4)

using a probability picture which focuses on the vector states; and

e^r(t) = ½v(t)H(t)v(t)^T

(5)

using a demographic picture which focuses on demographic properties of the histories.

5. Comments on Demographic Pictures

Given a finite non-empty set of full viable histories H, observing a face H_t ⊆ H at t produces a list of the available H_t ⊆ H and thus creates a list of possible modal demographies (n_α, p_α) ∈ A_t for all α ∈ H_t. Let |H_t| = h. List the h histories in a fixed order from α to χ, with row vector (n_t| = (n_α, …, n_χ) and column vector |p_t) = (p_α, …, p_χ)^T. So for histories α, …, χ ∈ H_t, we can write the demographic picture for |H_t| = h at t as (n_t|p_t) = H(t) where:

$$H\left(t\right)=\left(\begin{array}{ccc}{n}_1{p}_1& \dots & n_1{p}_h\\ ⋮& \ddots & ⋮\\ n_h{p}_1& \cdots & n_h{p}_h\end{array}\right)=\left(\begin{array}{ccc}2& \dots & n_1{p}_h\\ ⋮& \ddots & ⋮\\ n_h{p}_1& \cdots & 2\end{array}\right)$$

(6)

Each diagonal entry = 2 because a diagonal entry n_αp_α is determined by the modal demography (n_s, p_s) for each history, and n_sp_s = 2. Thus, using ½H(t) we can restate Equation (5):

$$\begin{array}{ll}{e}^{r\left(t\right)}& =½v\left(t\right)H\left(t\right)v{\left(t\right)}^T=½v\left(t\right)\left(\begin{array}{ccc}2& \dots & n_1{p}_h\\ ⋮& \ddots & ⋮\\ n_h{p}_1& \cdots & 2\end{array}\right)v{\left(t\right)}^T\\ & =v\left(t\right)\left(\begin{array}{ccc}1& \dots & ½n_1{p}_h\\ ⋮& \ddots & ⋮\\ ½n_h{p}_1& \cdots & 1\end{array}\right)v{\left(t\right)}^T\end{array}$$

(7)

Because the two-history case has some useful properties, we present much of our discussion on the two history version, which becomes:

$$\begin{gathered} e^{r(t)}=v\left(t\right)\left(\begin{array}{ccc}1& & ½n_1{p}_2\\ & & \\ ½n_2{p}_1& & 1\end{array}\right)v{\left(t\right)}^T,\mathrm{where} \\ ½H\left(t\right)=\left(\begin{array}{ccc}1& & ½n_1{p}_2\\ & & \\ ½n_2{p}_1& & 1\end{array}\right). \end{gathered}$$

(8)

Lemma 2.

Let H be a finite non-empty set of full viable histories. Let G be a non-trivial descent sequence using H, let H_t ⊆ H be the face of H observed at t, and let G(t) ∈ G be the generation at t with vector state v(t). Then r(t) = 0 only if ½H(t) = [1] at all entries.

Proof of Lemma 2.

Assume the premises. Equations (4)–(7) simply rearrange terms in ½Σ_iΣ_jv_i(t)v_j(t)n_ip_j. From the definition of modal demography, p_i = 2/n_i and p_j = 2/n_j. The values on the diagonal of ½H(t) are for each history α, ½n_αp_α = 1. We thus examine the off-diagonal products n_αp_χ and n_χp_α. Then n_ip_j = 2n_i/n_j and n_jp_i = 2n_j/n_i. Thus, 2n_i/n_j = 2n_j/n_i occurs only if n_i = n_j, in which case n_ip_j = n_jp_i = 2. This occurs only if all histories i and j have the same structural number or both have s = 2 or 3, and thus ½H(t) = [1] in all entries. Otherwise stated, in this case the value from Equation (3) is n_αχ = 2. ☐

Implications of Lemma 2: knowing the modal demography of histories in H we can compute a proposed population growth rate r(t).

• The result n_α = n_χ occurs if structural numbers s_α, s_χ are <4 or whenever s_α = s_χ; so r(t) = 0. Otherwise, then Lemma 2 implies Lemma 1, which says that e^r(t) ≠ 1, and thus r(t) > 0. This occurs since n_αp_χ does not equal n_χp_α; thus from Lemma 1 and [8] the off-diagonal elements of ½H(t) implies adiabatic change in r(t).
• In discussions in physics, when n_αp_χ ≠ n_χp_α some claim that the resulting r(t) is “not commutative”. In physics, the “non-commutative” result actually means switching which experiment is taken, then comparing their results; in physics when changing the order of the products it also means changing the experiment; but this comparison of the two results also creates an equation that looks like our Equations (1), (2), (7) or (8). However, in physics reversing the experiment causes different measurements, which causes the physical uncertainty between the two results. In contrast, the seemingly “non-commuting” values in culture theory exist because the equation for computing r(t) requires computing both “directions” of the modal demography of histories in H (similar to comparing both directions of the physics model), and if any two (or more) of those have histories of distinct structural numbers (at least one >3), so that one or more n_αχ > 2 (see Equation (3)), then n_χp_α ≠ n_αp_χ. Culture theory thus predicts adiabatic demographic change, not uncertainty, from a mechanism similar to that which causes uncertainty in physics.

6. Comments on Probability Pictures

Lemma 3.

A probability picture V(t) is symmetric, Σ_iΣ_jv_i(t)v_j(t) = 1 and Σ_iΣ_j(Δ_ij(t)) = 0.

Proof of Lemma 3.

In Equation (4) V(t) is symmetric since each pair v_i(t)v_j(t) = v_j(t)v_i(t). Since Σ_αv_α(t) = 1 then v(t)v(t)^T = Σ_iΣ_jv_i(t)v_j(t) = 1. At t + ε ≥ t (ε < t − (t − 1)) then Σ_αv_α(t + ε) = 1: so Σ_iΣ_jv_i(t + ε)v_j(t + ε) = 1; so Σ_iΣ_j(v_ij(t + ε) − v_ij(t)) = Σ_iΣ_j(Δ_ij(t)) = 1 − 1 = 0. ☐

Since we discuss paths of histories, a frequency-domain representation of vector states is useful.

Definition 7.

Let r₁, r₂, r₃ be real numbers such that r₁² + r₂² + r₃² = 1. Let R be a set of 2 by 2 matrices with complex entries that forms a ring with respect to matrix addition and multiplication. Let R ⊆ R be a set of hermitian idempotent matrices of R; and let R ∈ R be such that R = ½[r_ij] where r₁₁ = 1 + r₃, r₂₂ = 1 − r₃, r₂₁ = r₁ + ir₂, r₁₂ = r₁ − ir₂. That is:

$$R=½\left[r_{ij}\right]=½\left(\begin{array}{cc}1+r_3 & r_1-i{r}_2\\ r_1+i{r}_2& 1-r_3\end{array}\right)$$

Following ([26], p. 30) we define matrices

$$1=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right),{\Sigma }_1=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right),{\Sigma }_2=\left(\begin{array}{cc}0& -i\\ +i& 0\end{array}\right),{\Sigma }_3=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)$$

and let z₀, z₁, z₂, z₃, be complex numbers such that R = z₀1 + z₁Σ₁ + z₂Σ₂ + z₃Σ₃ where:

z₀ = ½(r₁₁ + r₂₂), z₁ = ½(r₂₁ + r₁₂), z₂ = i½(r₂₁ − r₁₂), z₃ = ½(r₁₁ − r₂₂).

The four matrices 1, Σ₁, Σ₂, and Σ₃ are the standard Pauli spin matrices, where for R then z₀ = 1, z₁ = r₁, z₂ = r₂ and z₃ = r₃. Note that −1 ≤ r₁, r₂, r₃ ≤ 1. From ([27], p. 104) R is a set of non-trivial 2 by 2 version of R; a ring of such forms an orthomodular poset and indeed an atomic orthomodular lattice with the covering property, that is in 1-1 correspondence with the set of closed subspaces of a two-dimensional complex Hilbert space.

Definition 8.

Let H be a finite non-empty set of viable histories, let G be a non-trivial viable descent sequence using histories H_t ∈ H, let G_t ∈ G be a generation of G using a face H_t ∈ H at t, and let v(t) be the vector state of G_t.

• Let ₂H_t = {α, χ} ⊆ H_t be a two-history subset of H_t. Let R(t) = ½[r_ij(t)] be a projection, let r₁(t), r₂(t), and r₃(t) be real numbers such that r₁(t)² ₊ r₂(t)² + r₃(t)² = 1, such that 0 ≤ r₁(t) < 1, 0 ≤ r₂(t) < 1, and such that v_α(t) = ½r₁(t) = ½(1 + r₃(t)). Then R(t) is the status of G_t.
• A unit circle C is meant a set of points (x, y) in the plane R² which satisfy the equation x² + y² = 1.

Theorem 1.

Assume the premises of Definition 8. Let H be a finite non-empty set of viable histories having structural numbers s < 152 (see [8] for use of this limit). Let G be a descent sequence using H. Let R(t) be the status of H_t, and let v(t) be the vector state of H_t. Let ₂H_t = {α, χ} ⊆ H_t be a non-empty subset of H_t. Let t₂ > t₁ > t₀ define a path of v_α(t) from t = t₀ to t = t₂ such that v_α(t₀) = 1 changes monotonically to v_α(t₁) = 0 and then monotonically back to v_α(t₂) = 1. That is, let r₃ move from r₃(t₀) = 1 to r₃(t₁) = − 1 and then back to r₃(t₂) = 1. Let O(t) = (n(t), p(t), r(t)). Then:

(1) 

trR(t) = 1;

(2) 

v_χ(t) = ½(1 − r₃(t));

(3) 

the vector state v(t) of ₂H_t is given by the main diagonal of R(t);

(4) 

r(t) is a maximum when r₃ = 0.

Theorem 2.

Let r₁(t) = 0. Then: (i) R(t) has ΣΣ_ijr_ij(t) = 1; and (ii) the sum Σ∫r(t)dv(t) = 0 when summed over all paths (all variants of paths) of for pairs ₂H_t.

Theorem 3.

Let r₂(t) = 0. Then Σ∫r(t)dv(t) = 0 when summed over all paths (all variants of paths) of all pairs ₂H_t.

Proof of Theorem 1.

Assume the premises of Theorem 1. In a two history system, ₂H_t = {α, χ} ⊆ H_t is the vector state v(t) = (v_α(t), v_χ(t)) where v_χ(t) = 1 − v_α(t). R(t) is a status and since in a status v_α(t) = ½r₁₁ = ½(1 + r₃), and since v_α(t) + v_χ(t) = 1 in a two-history state, then v_χ(t) = ½r₂₂ = ½(1 − r₃). In addition, also then v_α(t) + v_χ(t) = ½(1 + r₃) + ½(1 − r₃) = 1 = trR(t), which establishes Theorems 1, 2, and 3. Establishing 4: We find r(t) is a maximum when r₃ = 0, given Theorem 1(1) and 1(3), and Lemma 1(2), so when r₃ = 0 then v(t) = (0.5, 0.5).

Let r₁(t) = 0 so

$$R(t)=½[r_{ii}]=½\left(\begin{array}{cc}1+r_3& -i{r}_2\\ i{r}_2& 1-r_3\end{array}\right)$$

and thus ½Σ_iΣ_jr_ij(t) = ½2 = 1 which establishes 1(1).

Let H_t = {α, χ}. At time t, H_t picks a set of modal demographies A_t = {(n_α, p_α), (n_χ, p_χ)} and v(t) acts as a linear operator on A_t; so we get

v(t)A_t = Σ_αv(t)(n_α, p_α) = (n(t), p(t)) for all α ∈ H_t.

From Lemma 2, O(t) = (n(t), p(t), e(t)) are the predicted results at t; when s_α ≠ s_χ then (n_α, p_α) ≠ (n_χ, p_χ). R(t) is an idempotent Hermitian matrix per Definition 7, and under the premises has r₁ = 0. Then r₂² + r₃² = 1. We have a two history system with vector state v(t) = (v_α(t), v_χ(t)) where v_χ(t) = 1 − v_α(t), and where v_α(t) = ½r₁₁ = ½(1 + r₃(t)). We let t₂ > t₁ > t₀ define a path from t = t₀ to t = t₂ such that v_α(t₀) = 1 changes monotonically to v_α(t₁) = 0 and then monotonically again to v_α(t₂) = 1, which occurs as r₃(t) moves monotonically from r₃(t) = 1 to r₃(t) = −1 and then back to r₃(t) = 1. At each t, given r₃(t), we compute r₂(t)² = 1 − r₃(t)². Then r₂(t)² + r₃(t)² = 1 traces a unit circle C. Theorems 2 and 3 then follow from Green’s theorem. □

Observation 2.

Let G be a population, G_t ∈ G with the sub-populations G_t using the set of histories using face H_t ∈ H, and let v(t) be the vector state of G_t. Assume history α ∈ H_t, α ∈ H_t+1, and v_α(t) = v_α(t + 1) = 1. Then from t to t + 1, v(t) forms a loop. That is, the minimal descent sequence of any viable pure system α also forms a loop, indicated also since the minimal structure of α is a group. So any pure system is a loop. Diagrams like Figure 1 could occur when v(t) is not simply a pure system. Describing probability pictures by complex Hilbert spaces (Definition 7) can assist predicting demographic pictures, using pure systems as the basis of computing n(t), p(t) hence r(t).

7. Discussion

Following the examples of [1,2] we here study systems in which the cultural organization is based on kinship descriptions using natural languages. In both cases, our theory makes predictions on population measures on the observed outcome of the kinship systems at stated times. Our Observation 1 and Lemma 1 predict what is found empirically: either single history systems and specific (n_s, p_s) pairs by the structural number of the identified history; or systems undergoing change in their culture. In that case the (n_s, p_s) pairs are changing and we can predict that rate of change yielding both the n(t) and p(t) for the given t, and the value of the adiabatic growth rate r(t) at t. An example of this prediction of rate of change in western Europe for about 1000 years from about AD 1000 to 1950 is given in [1]. The time period of that study was about 1000 years of human history in a defined area.

Thus, study of the homotopy groups resulting from Definitions 5, 7 and 8 may thus tell us a lot about the possible paths of the empirical demography of cultures. Definitions 7 and 8 assume no physical model, but we can use their math to study the changes in vector states on histories on the predicted n(t), p(t) and r(t) of the society per generation. The methods of [28,29] and many other current works such as [30] in social sciences use complex Hilbert spaces to describe models of how “cognition” works, using much shorter time periods, and to otherwise interpret how societies of individuals can describe and change the world around them. Hilbert space probability models per [31], which is a foundation paper for [13], are quite close to the Pauli model used here to describe changes in cultural systems; they differ from ours in their application. In particular, [31], Postulate 4 does not apply here since the applications are distinct. However, the probabilities of [30,31] are averages of probabilities on a population, not predictions of individual probabilities. There may be thus be many ways to discuss evolution of cultural systems using complex Hilbert spaces that have simply not yet been tried.

In this paper, in [17], and in both [30,31] the mathematical foundation starts with representation of the basic objects as languages; ours are natural languages. Kinship systems are derived from non-associative algebras [20,32] which in natural languages may allow groups to occur. Cultural systems with different dictionaries but similar groups are studied as isotopic kinship terminologies for example [8,11], which is a separate topic mathematically and empirically from study of languages [9,10,11,12,13]. Ref. [33] says “… kinship organizations are based on terminologies, which have their own distinctive logical structure centered on a “self” or I position. Language does not have a structure of this kind …”. So while kinship terminologies occur as part of natural languages, kinship analysis is not the same as the study of the language.

Our study also helps identify what cannot be predicted by this method. For example, sociologists and anthropologists use relationship studies to describe how individuals are “related”; the minimal structure defined here based on assignments made based on the “principles” used to arrange or avoid marriages, given the natural language and the history; they do not define which specific individuals are in fact assigned to each relation. In contrast, in genetic inbreeding experiments Sewall Wright [34] at diagrams 7.1(a), 7.12, 7.16 and others used the minimal structure of kinship relations for illustrating inbreeding arrangements; but in those situations, the individuals are not “assigned”—they are the actual kin of the identified sources.

The ability to derive population measures from the language-based statement of rules is something new to science, and should be explored. Many other things also affect population change, and are not explored here.