On the Calculation of Sample Entropy Using Continuous and Discrete Human Gait Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Biological Data
2.2. Generated Data
2.3. Data Processing
2.4. Statistical Analysis
3. Results
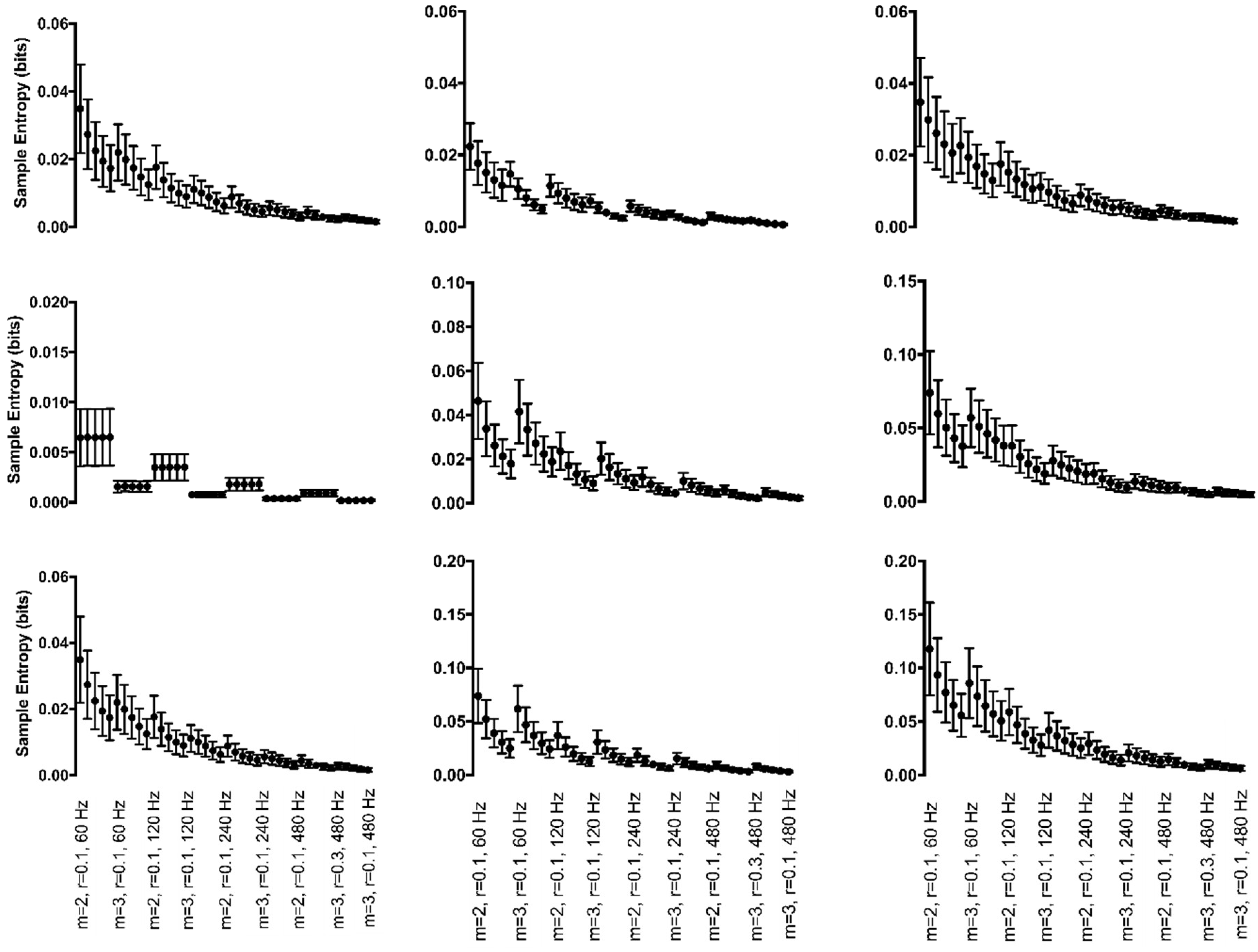
3.1. Joint Angle Data
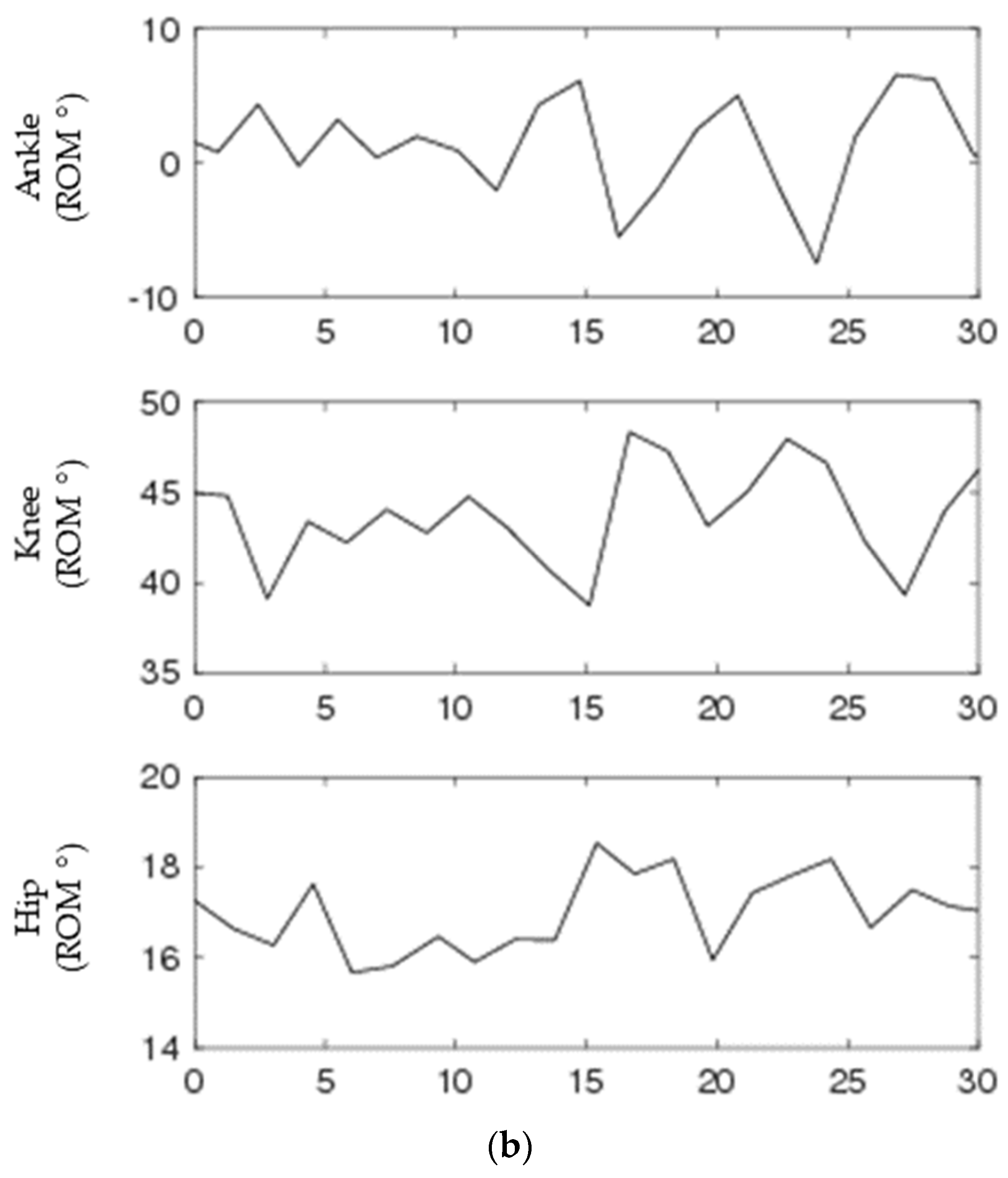
3.2. Biological Range of Motion Data
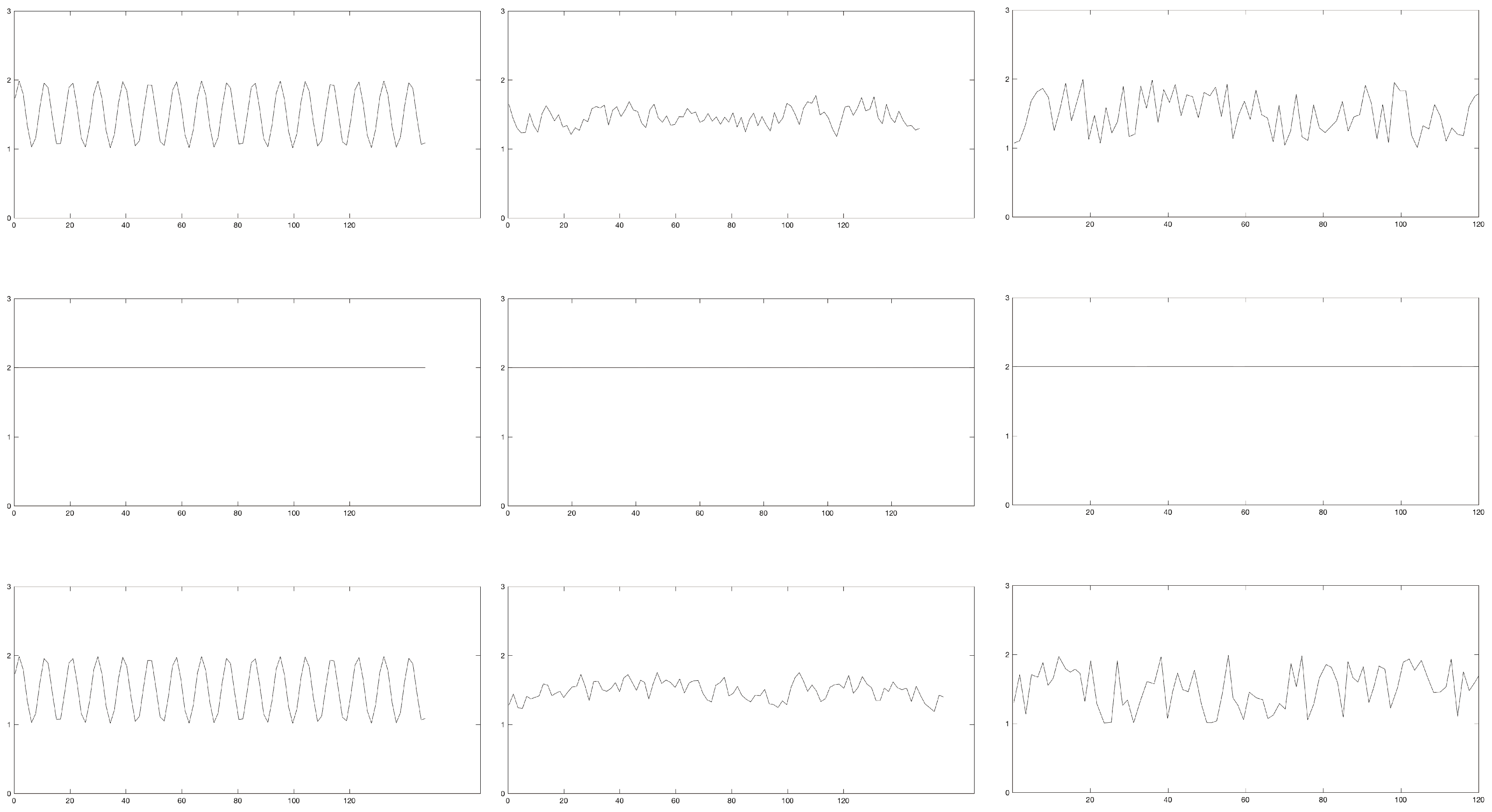
3.3. Continuous, Generated Data
3.3.1. Periodic Manipulations
3.3.2. Chaotic Manipulations
3.3.3. Random Manipulations
3.4. Discrete, Generated Data
3.4.1. Periodic Manipulations
3.4.2. Chaotic Manipulations
3.4.3. Random Manipulations
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Nat. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S.M.; Gladstone, I.M.; Ehrenkranz, R.A. A regularity statistic for medical data analysis. J. Clin. Monit. 1991, 7, 335–345. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S.M.; Viscarello, R.R. Approximate entropy: A regularity measure for fetal heart rate analysis. Obstet. Gynecol. 1992, 79, 249–255. [Google Scholar] [PubMed]
- Fleisher, L.A.; Pincus, S.M.; Rosenbaum, S.H. Approximate entropy of heart rate as a correlate of postoperative ventricular dysfunction. Anesthesiology 1993, 78, 683–692. [Google Scholar] [CrossRef] [PubMed]
- Sleigh, J.W.; Donovan, J. Comparison of bispectral index, 95% spectral edge frequency and approximate entropy of the EEG, with changes in heart rate variability during induction of general anaesthesia. Br. J. Anaesth. 1999, 82, 666–671. [Google Scholar] [CrossRef] [PubMed]
- Ryan, S.M.; Goldberger, A.L.; Pincus, S.M.; Mietus, J.; Lipsitz, L.A. Gender and age-related differences in heart rate dynamics: Are women more complex than men? J. Am. Coll. Cardiol. 1994, 24, 1700–1707. [Google Scholar] [CrossRef]
- Liu, C.C.; Shao, P.; Li, L.; Sun, X.; Wang, X.P.; Liu, F. Comparison of different threshold values r for approximate entropy: application to investigate the heart rate variability between heart failure and healthy control groups. Physiol. Meas. 2011, 32, 167–180. [Google Scholar] [CrossRef] [PubMed]
- Yeragani, V.K.; Sobolewski, E.; Jampala, V.C.; Kay, J.; Yeragani, S.; Igel, G. Fractal dimension and approximate entropy of heart period and heart rate: awake versus sleep differences and methodological issues. Clin. Sci. 1998, 95, 295–301. [Google Scholar] [CrossRef] [PubMed]
- Valenza, G.; Allegrini, P.; Lanatà, A.; Scilingo, E.P. Dominant Lyapunov exponent and approximate entropy in heart rate variability during emotional visual elicitation. Front. Neuroeng. 2012, 5, 3. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hartman, M.L.; Pincus, S.M.; Johnson, M.L.; Matthews, D.H.; Faunt, L.M.; Vance, M.L.; Thorner, M.O.; Veldhuis, J.D. Enhanced basal and disorderly growth hormone secretion distinguish acromegalic from normal pulsatile growth hormone release. J. Clin. Investig. 1994, 94, 1277–1288. [Google Scholar] [CrossRef] [PubMed]
- Caldirola, D.; Bellodi, L.; Caumo, A.; Migliarese, G.; Perna, G. Approximate Entropy of Respiratory Patterns in Panic Disorder. Am. J. Psychiatry 2004, 161, 79–87. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karmakar, C.K.; Khandoker, A.H.; Begg, R.K.; Palaniswami, M.; Taylor, S. Understanding ageing effects by approximate entropy analysis of gait variability. In Proceedings of the 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007. [Google Scholar]
- Khandoker, A.H.; Palaniswami, M.; Begg, R.K. A comparative study on approximate entropy measure and poincaré plot indexes of minimum foot clearance variability in the elderly during walking. J. Neuroeng. Rehabil 2008, 5, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Yentes, J.M.; Hunt, N.; Schmid, K.K.; Kaipust, J.P.; McGrath, D.; Stergiou, N. The appropriate use of approximate entropy and sample entropy with short data sets. Ann. Biomed. Eng. 2013, 41, 349–365. [Google Scholar] [CrossRef] [PubMed]
- Yentes, J.M.; Denton, W.; McCamley, J.; Raffalt, P.C.; Schmid, K.K. Effect of parameter selection on entropy calculation for long walking trials. Gait Posture 2018, 60, 128–134. [Google Scholar] [CrossRef] [PubMed]
- Moraiti, C.O.; Stergiou, N.; Ristanis, S.; Vasiliadis, H.S.; Patras, K.; Lee, C. The Effect of Anterior Cruciate Ligament Reconstruction on Stride-to-Stride Variability. Arthrosc. J. Arthrosc. Relat. Surg. 2009, 25, 742–749. [Google Scholar] [CrossRef] [PubMed]
- Georgoulis, A.D.; Moraiti, C.; Ristanis, S.; Stergiou, N. A novel approach to measure variability in the anterior cruciate ligament deficient knee during walking: The use of the approximate entropy in orthopaedics. J. Clin. Monit. Comput. 2006, 20, 11–18. [Google Scholar] [CrossRef] [PubMed]
- Stergiou, N. Nonlinear Analysis for Human Movement Variability; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Stergiou, N.; Harbourne, R.; Cavanaugh, J. Optimal movement variability: a new theoretical perspective for neurologic physical therapy. J. Neurol. Phys. Ther. 2006, 30, 120–129. [Google Scholar] [CrossRef] [PubMed]
- Leverick, G.; Szturm, T.; Wu, C.Q. Using entropy measures to characterize human locomotion. J. Biomech. Eng. 2014, 136, 121002. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol Heart Circ. Physiol. 2000, 278, H2039–2049. [Google Scholar] [CrossRef] [PubMed]
- Rhea, C.K.; Wutzke, C.J.; Lewek, M.D. Gait dynamics following variable and constant speed gait training in individuals with chronic stroke. Gait Posture 2012, 36, 332–334. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stergiou, N. Amputation effects on the underlying complexity within transtibial amputee ankle motion. Chaos 2014, 24, 013140. [Google Scholar] [CrossRef]
- Terada, M.; Bowker, S.; Thomas, A.C.; Pietrosimone, B.; Hiller, C.E.; Rice, M.S. Alterations in stride-to-stride variability during walking in individuals with chronic ankle instability. Hum. Mov. Sci. 2015, 40, 154–162. [Google Scholar] [CrossRef] [PubMed]
- Lamoth, C.J.C.; Ainsworth, E.; Polomski, W.; Houdijk, H. Variability and stability analysis of walking of transfemoral amputees. Med. Eng. Phys. 2010, 32, 1009–1014. [Google Scholar] [CrossRef] [PubMed]
- Rispens, S.M.; Van Dieën, J.H.; Van Schooten, K.S.; Cofré Lizama, L.E.; Daffertshofer, A.; Beek, P.J. Fall-related gait characteristics on the treadmill and in daily life. J. Neuroeng. Rehabil. 2016, 13, 12. [Google Scholar] [CrossRef] [PubMed]
- Raffalt, P.C.; McCamley, J.; Denton, W.; Yentes, J.M. Sampling frequency influences sample entropy of kinematics during walking. Med. Biol. Eng. Comput. 2018. submitted. [Google Scholar]
- Powell, D.W.; Szekely, B.; Blackmore, S.E.; Nelson, A.; Schallert, A.; Lester, D.B. Effects of Sampling Rate and Movement Frequency on Entropic Measures of Effects of Sampling Rate and Movement Frequency on Entropic Measures of Regularity. J. Nat. Sci. 2018, 4, e504. [Google Scholar]
- Xinnian, C.; Solomon, I.C.; Chon, K.H. Comparison of the Use of Approximate Entropy and Sample Entropy: Applications to Neural Respiratory Signal. In Proceedings of the Engineering in Medicine and Biology 27th Annual Conference, Shanghai, China, 17–18 January 2006. [Google Scholar]
- Govindan, R.B.; Wilson, J.D.; Eswaran, H.; Lowery, C.L.; Preißl, H. Revisiting sample entropy analysis. Phys. A Stat. Mech. Appl. 2007, 376, 158–164. [Google Scholar] [CrossRef]
- Powell, D.W.; Szekely, B.; Blackmore, S.E.; Nelson, A.; Schallert, A.; Lester, D.B. Effects of Sampling Rate and Movement Frequency on Entropic Measures of Regularity. J. Nat. Sci. 2018, 4, e504. [Google Scholar]
- Thuraisingham, R.A.; Gottwald, G.A. On multiscale entropy analysis for physiological data. Phys. A Stat. Mech. Appl. 2006, 366, 323–332. [Google Scholar] [CrossRef]
- Vaillancourt, D.E.; Sosnoff, J.J.; Newell, K.M. Age related changes in complexity depend on task dynamics. J. Appl. Physiol. 2004, 97, 454–455. [Google Scholar] [CrossRef] [PubMed]
- Van Emmerik, R.E.A.; Ducharme, S.W.; Amado, A.C.; Hamill, J. Comparing dynamical systems concepts and techniques for biomechanical analysis. J. Sport Heal. Sci. 2016, 5, 3–13. [Google Scholar] [CrossRef]
- Hausdorff, J.M.; Ashkenazy, Y.; Peng, C.K.; Ivanov, P.C.; Stanley, H.E.; Goldberger, A.L. When human walking becomes random walking: Fractal analysis and modeling of gait rhythm fluctuations. Phys. A Stat. Mech. Appl. 2001, 302, 138–147. [Google Scholar] [CrossRef]
- Cappozzo, A.; Della Croce, U.; Leardini, A.; Chiari, L. Human movement analysis using stereophotogrammetry: Part 1: theoretical background. Gait Posture 2005, 21, 186–196. [Google Scholar] [CrossRef] [PubMed]
- Joint Angle Visual3D Wiki Documentation n.d. Available online: https://www.c-motion.com/v3dwiki/index.php?title=Joint_Angle#Visual3D_Default_Joint_Angle_Conventions (accessed on 20 August 2018).
- Reinschmidt, C.; Van Den Bogert, A.J.; Lundberg, A.; Nigg, B.M.; Murphy, N.; Stacoff, A. Tibiofemoral and tibiocalcaneal motion during walking: External vs. Skeletal markers. Gait Posture 1997, 6, 98–109. [Google Scholar] [CrossRef]
- Ahmadi, S.; Sepehri, N.; Wu, C.; Szturm, T. Sample Entropy of Human Gait Center of Pressure Displacement: A Systematic Methodological Analysis. Entropy 2018, 20, 579. [Google Scholar] [CrossRef]
- Buzzi, U.H.; Stergiou, N.; Kurz, M.J.; Hageman, P.A.; Heidel, J. Nonlinear dynamics indicates aging affects variability during gait. Clin. Biomech. 2003, 18, 435–443. [Google Scholar] [CrossRef] [Green Version]
- Hausdorff, J.M.; Cudkowicz, M.E.; Firtion, R.; Wei, J.Y.; Goldberger, A.L. Gait variability and basal ganglia disorders: Stride-to-stride variations of gait cycle timing in Parkinson’s disease and Huntington’s disease. Mov Disord. 1998, 13, 428–437. [Google Scholar] [CrossRef] [PubMed]
- Ramdani, S.; Bouchara, F.; Lagarde, J. Influence of noise on the sample entropy algorithm. Chaos 2009, 19. [Google Scholar] [CrossRef] [PubMed]







| 60 Hz | 120 Hz | 240 Hz | 480 Hz | |
|---|---|---|---|---|
| Biological Data | ||||
| Ankle Angle | 8 (5–10) | 16 (10–20) | 31(20–39) | 62 (40–78) |
| Knee Angle | 10 (8–12) | 18 (15–23) | 36 (30–46) | 72 (59–92) |
| Hip Angle | 13 (11–17) | 26 (22–33) | 51(44–65) | 102 (87–130) |
| Generated Data | ||||
| Periodic Manipulations | 13 (6–17) | 26 (12–34) | 52 (24–68) | 104 (48–136) |
| Chaotic Manipulations | 13 (6–17) | 26 (12–34) | 52 (24–68) | 104 (48–136) |
| Random Manipulations | 13 (6–17) | 26 (12–34) | 52 (24–68) | 104 (48–136) |
| Joint Angle | Range of Motion | ||||
|---|---|---|---|---|---|
| Model | F-Value | p-Value | F-Value | p-Value | |
| Ankle | Hz | 294.7 | < 0.0001 | 0.68 | 0.58 |
| m | 255.5 | < 0.0001 | 0.57 | 0.49 | |
| r | 105.9 | < 0.0001 | 136.9 | < 0.0001 | |
| Hz*m | 249.6 | < 0.0001 | 1.1 | 0.37 | |
| Hz*r | 114.3 | < 0.0001 | 1.1 | 0.39 | |
| m*r | 7.2 | < 0.0001 | 0.46 | 0.77 | |
| Hz*m*r | 6.9 | < 0.0001 | 1.0 | 0.43 | |
| Knee | Hz | 481.8 | < 0.0001 | 8.3 | 0.02 |
| m | 84.0 | < 0.0001 | 0.01 | 0.92 | |
| r | 35.1 | < 0.0001 | 42.5 | < 0.0001 | |
| Hz*m | 86.7 | < 0.0001 | 1.1 | 0.40 | |
| Hz*r | 38.4 | < 0.0001 | 2.3 | 0.04 | |
| m*r | 7.9 | < 0.0001 | 1.4 | 0.33 | |
| Hz*m*r | 8.9 | < 0.0001 | 0.40 | 0.95 | |
| Hip | Hz | 204.9 | < 0.0001 | 0.10 | 0.96 |
| m | 188.9 | < 0.0001 | 0.41 | 0.57 | |
| r | 40.0 | < 0.0001 | 37.9 | < 0.0001 | |
| Hz*m | 193.0 | < 0.0001 | 1.5 | 0.28 | |
| Hz*r | 31.0 | < 0.0001 | 1.9 | 0.07 | |
| m*r | 1.6 | 0.20 | 0.22 | 0.92 | |
| Hz*m*r | 1.7 | 0.09 | 4.7 | < 0.0001 | |
| Periodic Manipulation | Chaotic Manipulation | Random Manipulation | |||||
|---|---|---|---|---|---|---|---|
| Model | F-Value | p-Value | F-Value | p-Value | F-Value | p-Value | |
| Cycle amplitude | Hz | 40.5 | < 0.0001 | 273.0 | < 0.0001 | 220.3 | < 0.0001 |
| m | 16921.0 | < 0.0001 | 308.9 | < 0.0001 | 207.7 | < 0.0001 | |
| r | 140.9 | < 0.0001 | 249.1 | < 0.0001 | 224.5 | < 0.0001 | |
| Hz*m | 40.2 | < 0.0001 | 296.6 | < 0.0001 | 217.9 | < 0.0001 | |
| Hz*r | 16.0 | < 0.0001 | 252.9 | < 0.0001 | 226.2 | < 0.0001 | |
| m*r | 140.7 | < 0.0001 | 287.7 | < 0.0001 | 206.7 | < 0.0001 | |
| Hz*m*r | 15.8 | < 0.0001 | 272.6 | < 0.0001 | 218.4 | < 0.0001 | |
| Cycle period | Hz | 225.7 | < 0.0001 | 211.1 | < 0.0001 | 219.7 | < 0.0001 |
| m | 201.6 | < 0.0001 | 19.2 | 0.001 | 157.1 | < 0.0001 | |
| r | 1.4 | 0.27 | 204.1 | < 0.0001 | 217.1 | < 0.0001 | |
| Hz*m | 219.2 | < 0.0001 | 30.6 | < 0.0001 | 158.7 | < 0.0001 | |
| Hz*r | 0.88 | 0.57 | 204.0 | < 0.0001 | 217.0 | < 0.0001 | |
| m*r | 1.1 | 0.38 | 226.4 | < 0.0001 | 217.1 | < 0.0001 | |
| Hz*m*r | 0.90 | 0.55 | 227.1 | < 0.0001 | 215.8 | < 0.0001 | |
| Cycle period and amplitude | Hz | 225.4 | < 0.0001 | 266.2 | < 0.0001 | 225.7 | < 0.0001 |
| m | 219.8 | < 0.0001 | 124.9 | < 0.0001 | 185.9 | < 0.0001 | |
| r | 224.9 | < 0.0001 | 273.7 | < 0.0001 | 245.5 | < 0.0001 | |
| Hz*m | 221.2 | < 0.0001 | 123.9 | < 0.0001 | 186.6 | < 0.0001 | |
| Hz*r | 223.1 | < 0.0001 | 273.2 | < 0.0001 | 245.8 | < 0.0001 | |
| m*r | 195.9 | < 0.0001 | 67.3 | < 0.0001 | 143.5 | < 0.0001 | |
| Hz*m*r | 196.9 | < 0.0001 | 51.0 | < 0.0001 | 143.7 | < 0.0001 | |
| Periodic | Chaotic | Random | |||||
|---|---|---|---|---|---|---|---|
| Model | F-Value | p-Value | F-Value | p-Value | F-Value | p-Value | |
| Cycle amplitude | Hz | 45.1 | < 0.0001 | 0.16 | 0.92 | 0.58 | 0.64 |
| m | 5472795 | < 0.0001 | 0.47 | 0.51 | 0.71 | 0.45 | |
| r | 246.1 | < 0.0001 | 236.3 | < 0.0001 | 50.9 | < 0.0001 | |
| Hz*m | 25.8 | < 0.0001 | 0.69 | 0.57 | 0.31 | 0.82 | |
| Hz*r | 25.6 | < 0.0001 | 0.17 | 1.0 | 0.41 | 0.96 | |
| m*r | 883.2 | < 0.0001 | 2.5 | 0.06 | 1.6 | 0.21 | |
| Hz*m*r | 13.5 | < 0.0001 | 0.57 | 0.86 | 1.0 | 0.43 | |
| Cycle period | Hz | 0.38 | 0.77 | 0.83 | 0.53 | 0.56 | 0.65 |
| m | 29.1 | < 0.0001 | 0.09 | 0.79 | 17.5 | 0.009 | |
| r | 1.8 | 0.15 | 54.3 | < 0.0001 | 81.2 | < 0.0001 | |
| Hz*m | 1.9 | 0.16 | 1.1 | 0.41 | 3.7 | 0.04 | |
| Hz*r | 0.87 | 0.58 | 0.86 | 0.59 | 1.3 | 0.22 | |
| m*r | 1.4 | 0.24 | 0.10 | 0.98 | 5.4 | 0.004 | |
| Hz*m*r | 0.78 | 0.67 | 1.1 | 0.39 | 2.2 | 0.02 | |
| Cycle period and amplitude | Hz | 45.1 | < 0.0001 | 1.5 | 0.23 | 0.70 | 0.56 |
| m | 5472795 | < 0.0001 | 0.44 | 0.53 | 0.02 | 0.90 | |
| r | 246.1 | < 0.0001 | 88.8 | < 0.0001 | 40.1 | < 0.0001 | |
| Hz*m | 25.8 | < 0.0001 | 0.55 | 0.65 | 0.52 | 0.67 | |
| Hz*r | 25.6 | < 0.0001 | 1.1 | 0.40 | 0.94 | 0.51 | |
| m*r | 883.2 | < 0.0001 | 0.54 | 0.71 | 2.7 | 0.06 | |
| Hz*m*r | 13.5 | < 0.0001 | 1.5 | 0.13 | 0.88 | 0.57 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
McCamley, J.D.; Denton, W.; Arnold, A.; Raffalt, P.C.; Yentes, J.M. On the Calculation of Sample Entropy Using Continuous and Discrete Human Gait Data. Entropy 2018, 20, 764. https://doi.org/10.3390/e20100764
McCamley JD, Denton W, Arnold A, Raffalt PC, Yentes JM. On the Calculation of Sample Entropy Using Continuous and Discrete Human Gait Data. Entropy. 2018; 20(10):764. https://doi.org/10.3390/e20100764
Chicago/Turabian StyleMcCamley, John D., William Denton, Andrew Arnold, Peter C. Raffalt, and Jennifer M. Yentes. 2018. "On the Calculation of Sample Entropy Using Continuous and Discrete Human Gait Data" Entropy 20, no. 10: 764. https://doi.org/10.3390/e20100764
APA StyleMcCamley, J. D., Denton, W., Arnold, A., Raffalt, P. C., & Yentes, J. M. (2018). On the Calculation of Sample Entropy Using Continuous and Discrete Human Gait Data. Entropy, 20(10), 764. https://doi.org/10.3390/e20100764





