Brute Force Composition Scanning with a CALPHAD Database to Find Low Temperature Body Centered Cubic High Entropy Alloys
Abstract
:1. Introduction
2. Computational Details
3. Results and Discussion
3.1. Selection of Alloys, Extending the HEA Temperature Range
3.2. Convergence Testing for Scanning Part of the Composition Space
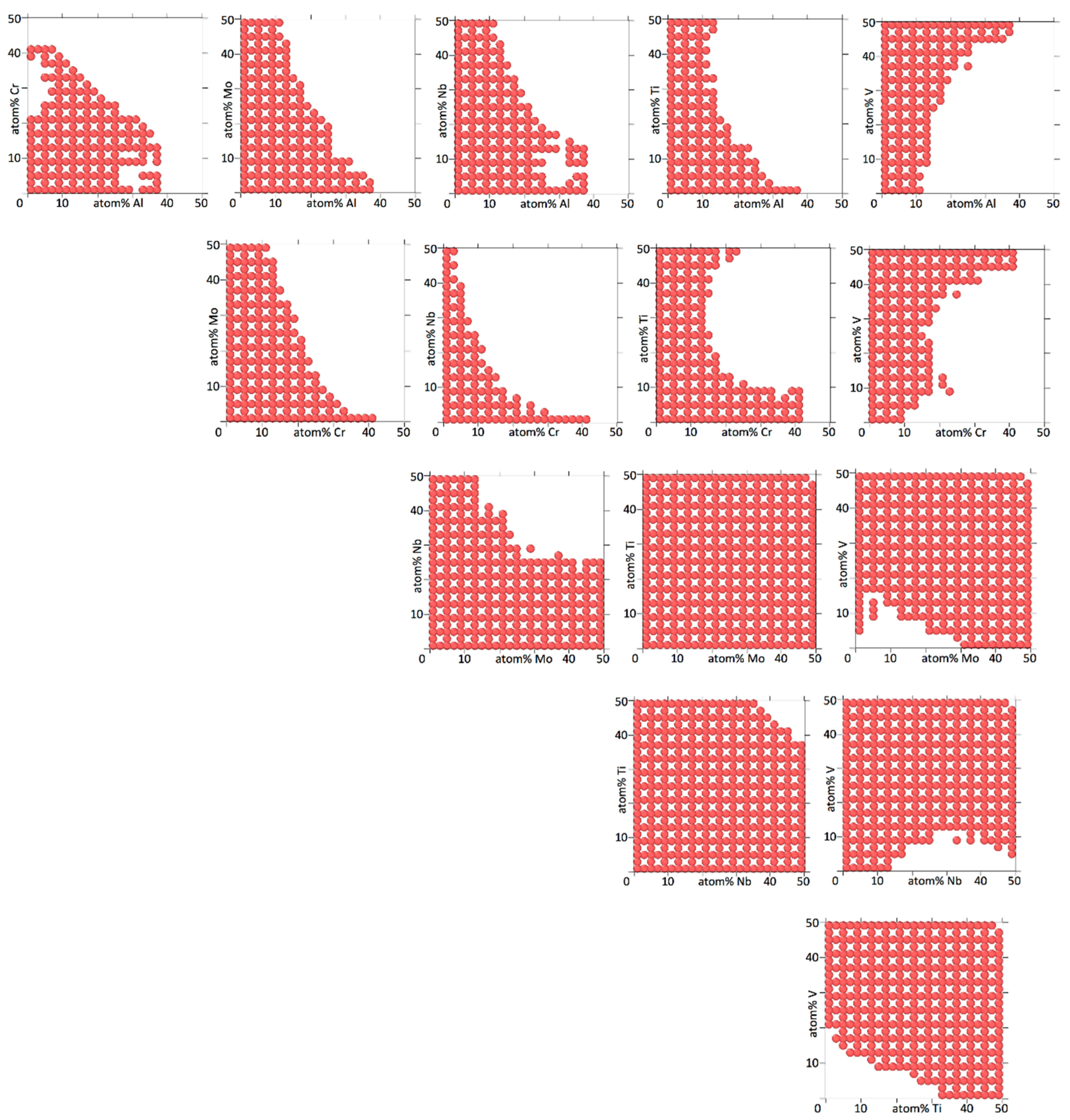
3.3. The Different Roles of Alloying Elements
3.4. Temperature Dependence of HEA Stability
3.5. HEA Island Centers
3.6. HEA Compositions with Minimum Concentration Constraints
3.7. Melting Temperature Ranges
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Maa, D.; Grabowski, B.; Körmann, F.; Neugebauer, J.; Raabe, D. Ab initio thermodynamics of the CoCrFeMnNi high entropy alloy: Importance of entropy contributions beyond the configurational one. Acta Mater. 2015, 100, 90–97. [Google Scholar] [CrossRef]
- Raabe, D.; Tasan, C.C.; Springer, H.; Bausch, M. From High-Entropy Alloys to High-Entropy Steels. Steel Res. Int. 2015, 86, 1127–1138. [Google Scholar] [CrossRef] [Green Version]
- Kivy, M.B.; Kriewall, C.S.; Zaeem, M.A. Formation of chromium-iron carbide by carbon diffusion in AlXCoCrFeNiCu high-entropy alloys. Mater. Res. Lett. 2018, 6, 321–326. [Google Scholar] [CrossRef]
- Li, Z.; Raabe, D. Strong and Ductile Non-equiatomic High-Entropy Alloys: Design, Processing, Microstructure, and Mechanical Properties. JOM 2017, 69, 2099–2106. [Google Scholar] [CrossRef] [Green Version]
- Gorsse, S.; Miracle, D.B.; Senkov, O.N. Mapping the world of complex concentrated alloys. Acta Mater. 2017, 135, 177–187. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Körmann, F.; Grabowski, B.; Neugebauer, J.; Raabe, D. Ab initio assisted design of quinary dual-phase high-entropy alloys with transformation-induced plasticity. Acta Mater. 2017, 136, 262–270. [Google Scholar] [CrossRef]
- Deng, Y.; Tasan, C.C.; Pradeep, K.G.; Springer, H.; Kostka, A.; Raabe, D. Design of a twinning-induced plasticity high entropy alloy. Acta Mater. 2015, 94, 124–133. [Google Scholar] [CrossRef]
- Uzera, B.; Picak, S.; Liu, J.; Jozaghi, T.; Canadinc, D.; Karaman, I.; Chumlyakov, Y.I.; Kireeva, I. On the mechanical response and microstructure evolution of NiCoCr single crystalline medium entropy alloys. Mater. Res. Lett. 2018, 6, 442–449. [Google Scholar] [CrossRef]
- Nene, S.S.; Frank, M.; Liu, K.; Mishra, R.S.; McWilliams, B.A.; Cho, K.C. Extremely high strength and work hardening ability in a metastable high entropy alloy. Sci. Rep. 2018, 8, 9920. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Wu, Y.; He, J.; Wang, H.; Liu, X.; An, K.; Wu, W.; Lu, Z. Phase-Transformation Ductilization of Brittle High-Entropy Alloys via Metastability Engineering. Adv. Mater. 2017, 29, 1701678. [Google Scholar] [CrossRef] [PubMed]
- Lilensten, L.; Couzinié, J.; Bourgon, J.; Perrière, L.; Dirras, G.; Prima, F.; Guillot, I. Design and tensile properties of a bcc Ti-rich high-entropy alloy with transformation-induced plasticity. Mater. Res. Lett. 2017, 5, 110–116. [Google Scholar] [CrossRef]
- Luo, H.; Li, Z.; Raabe, D. Hydrogen enhances strength and ductility of an equiatomic high-entropy alloy. Sci. Rep. 2017, 7, 9892. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, M.C.; Alman, D.E. Searching for Next Single-Phase High-Entropy Alloy Compositions. Entropy 2013, 15, 4504–4519. [Google Scholar] [CrossRef] [Green Version]
- Guruvidyathri, K.; Kumar, K.C.H.; Yeh, J.W.; Murty, B.S. Topologically Close-packed Phase Formation in High Entropy Alloys: A Review of Calphad and Experimental Results. JOM 2017, 69, 2113–2124. [Google Scholar] [CrossRef]
- Saal, J.E.; Berglund, I.S.; Sebastian, J.T.; Liaw, P.K.; Olson, G.B. Equilibrium high entropy alloy phase stability from experiments and thermodynamic modeling. Scripta Mater. 2018, 146, 5–8. [Google Scholar] [CrossRef]
- Otto, F.; Dlouhý, A.; Pradeep, K.G.; Kuběnová, M.; Raabe, D.; Eggeler, G.; George, E.P. Decomposition of the single-phase high-entropy alloy CrMnFeCoNi after prolonged anneals at intermediate temperatures. Acta Mater. 2016, 112, 40–52. [Google Scholar] [CrossRef] [Green Version]
- Mao, H.; Chen, H.; Chen, Q. TCHEA1: A Thermodynamic Database Not Limited for “High Entropy” Alloys. J. Phase Equilib. Diffus. 2017, 38, 353–368. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Mao, H.; Chen, Q. Database development and Calphad calculations for high entropy alloys: Challenges, strategies, and tips. Mater. Chem. Phys. 2018, 210, 279–290. [Google Scholar] [CrossRef]
- Senkov, O.N.; Miller, J.D.; Miracle, D.B.; Woodward, C. Accelerated exploration of multi-principal element alloys for structural applications. CALPHAD 2015, 50, 32–48. [Google Scholar] [CrossRef]
- Senkov, O.N.; Miller, J.D.; Miracle, D.B.; Woodward, C. Accelerated exploration of multi-principal element alloys with solid solution phases. Nat. Commun. 2015, 6, 6529. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Menou, E.; Toda-Caraballo, I.; Pineau, C.; Bertrand, E.; Ramstein, G.; Tancret, F. Evolutionary design of strong and stable high entropy alloys using multi-objective optimisation based on physical models, statistics and thermodynamics. Mater. Des. 2018, 143, 185–195. [Google Scholar] [CrossRef]
- Abu-Odeh, A.; Galvan, E.; Kirk, T.; Mao, H.; Chen, Q.; Mason, P.; Malak, R.; Arróyave, R. Efficient exploration of the High Entropy Alloy composition-phase space. Acta Mater. 2018, 152, 41–57. [Google Scholar] [CrossRef]
- Gheribi, A.E.; Pelton, A.D.; Bélisle, E.; le Digabel, S.; Harvey, J.-P. On the prediction of low-cost high entropy alloys using new thermodynamic multi-objective criteria. Acta Mater. 2018, 161, 73–82. [Google Scholar] [CrossRef]
- Tang, Z.; Gao, M.C.; Diao, H.; Yang, T.; Liu, J.; Zuo, T.; Zhang, Y.; Lu, Z.; Cheng, Y.; Zhang, Y.; et al. Aluminum Alloying Effects on Lattice Types, Microstructures, and Mechanical Behavior of High-Entropy Alloys Systems. JOM 2013, 65, 1848–1858. [Google Scholar] [CrossRef]












| Concentration Spacing (%) | Compositions | |
|---|---|---|
| Five elements | Six elements | |
| 6 | 13,530 | 74,412 |
| 4 | 60,905 | 473,382 |
| 2 | 862,750 | 2,114,580 * |
| Distance and Boundary Criteria | ||||
|---|---|---|---|---|
| Euclidean Distance | Manhattan distance | |||
| Boundary_on | Boundary_off | Boundary_on | Boundary_off | |
| % Al Cr Mn Nb Ti V | ||||
| island centre(s) | 1 1 1 25 31 41 | 1 1 1 23 25 49 | 1 3 1 21 37 37 * 1 1 13 5 39 41 * | 1 3 1 21 25 49 * |
| 1st nearest non-HEA | 0 0 0 22 28 50 10.1% from center | 11 1 1 17 25 45 12.3% from center | 1 11 1 21 29 37 7 1 5 5 41 41 16% from center | 1 11 1 25 13 49 24% from center |
| 2nd nearest non-HEA | 0 0 0 21 29 50 10.2% from center | 9 1 1 17 29 43 12.3% from center | 1 11 1 21 33 33 7 1 9 1 41 41 16% from center | 1 11 1 25 17 45 24% from center |
| 3rd nearest non-HEA | 0 0 0 23 27 50 10.2% from center | 1 9 1 27 17 45 12.6% from center | 1 11 1 21 37 29 7 1 13 1 41 37 16% from center | 1 11 1 25 21 41 24% from center |
| 4th nearest non-HEA | 0 0 1 21 28 50 10.4% from center | 1 9 1 27 21 41 12.6% from center | 9 3 1 13 37 37 9 1 11 1 37 41 16% from center | 1 1 11 25 21 41 24% from center |
| 5th nearest non-HEA | 0 0 1 22 27 50 10.4% from center | 9 1 1 15 29 45 12.6% from center | 9 3 1 17 33 37 9 1 11 5 33 41 16% from center | 1 9 1 27 13 49 24% from center |
| Island Center(s) and Distance to Nearest Non-HEA Composition | ||||
|---|---|---|---|---|
| Euclidean Distance | Manhattan Distance | |||
| Boundary_on | Boundary_off | Boundary_on | Boundary_off | |
| Alloy | % Elements | |||
| AlCrMnNbTiV | 1 1 1 25 31 41 10.1% | 1 1 1 23 25 49 12.3% | 1 3 1 21 37 37 * 1 1 13 5 39 41 * 16% | 1 3 1 21 25 49 * 24% |
| AlCrMoNbTiV | 1 1 37 1 21 39 * 10.2% | 1 1 37 1 13 47 * 11.3% | 1 1 39 1 21 37 * 20% | 1 1 35 1 13 49 * 24% |
| AlCrFeTiV | 11 43 1 1 44 * 2.4% | 11 43 1 1 44 * 2.4% | 11 43 1 1 44 * 4% | 11 43 1 1 44 * 4% |
| AlCrMnMoTi | 22 33 1 1 43 * 3.7% | 22 33 1 1 43 * 3.7% | 22 33 1 1 43 * 6% | 22 33 1 1 43 * 6% |
| Island Center(s) and Distance to Nearest Non-HEA Composition | ||||
|---|---|---|---|---|
| Euclidean Distance | Manhattan Distance | |||
| Boundary_on | Boundary_off | Boundary_on | Boundary_off | |
| Alloy, Constraint | % Al Cr Mn Nb Ti V | |||
| AlCrMnNbTiV Al ≥ 15% | 25 7 25 1 1 41 * 21 7 21 1 9 41 * 7.5% | 25 1 23 1 1 49 9.8% | 25 7 21 1 5 41 * 12% | 21 5 21 1 5 47 * 16% |
| AlCrMnNbTiV Cr ≥ 15% | 17 15 17 1 9 41 5.7% | 11 17 13 1 9 49 * 6.3% | 5 17 5 11 17 45 * 17 17 13 1 9 43 * 8% | 11 17 13 1 9 49 * 12% |
| AlCrMnNbTiV Al + Cr ≥ 15% | 25 7 25 1 1 41 * 21 7 21 1 9 41 * 7.5% | 25 1 23 1 1 49 9.8% | 25 7 21 1 5 41 * 7 9 5 17 21 41 * 12% | 21 5 21 1 5 47 * 7 9 5 13 17 49 16% |
| AlCrMoNbTiV Al ≥ 15% | 17 1 9 21 9 43 * 17 5 21 1 11 45 * 4.9% | 15 1 5 21 9 49 * 6.3% | 17 1 9 21 9 43 * 17 5 21 1 11 45 * 8% | 15 1 5 21 9 49 * 12% |
| AlCrMoNbTiV Cr ≥ 15% | 9 15 21 1 13 41 * 4.9% | 15 17 1 5 13 49 13 17 11 1 9 49 * 4.9% | 9 15 21 1 13 41 * 8% | 15 17 1 5 13 49 13 17 11 1 9 49 * 8% |
| AlCrMoNbTiV Al + Cr ≥ 15% | 9 7 29 1 13 41 * 6.3% | 11 5 25 1 9 49 * 7.5% | 9 7 29 1 13 41 * 12% | 11 5 25 1 9 49 * 16% |
| AlCrFeTiV Al ≥ 15% | 23 36 1 1 39 * 1.4% | 23 36 1 1 39 * 1.4% | 23 36 1 1 39 * 2% | 23 36 1 1 39 * 2% |
| AlCrFeTiV Cr ≥ 15% | 11 43 1 1 44 * 2.4% | 11 43 1 1 44 * 2.4% | 11 43 1 1 44 * 4% | 11 43 1 1 44 * 4% |
| AlCrFeTiV Al + Cr ≥ 15% | 11 43 1 1 44 * 2.4% | 11 43 1 1 44 * 2.4% | 11 43 1 1 44 * 4% | 11 43 1 1 44 * 4% |
| AlCrMnMoTi Al ≥ 15% | 22 33 1 1 43 * 3.7% | 22 33 1 1 43 * 3.7% | 22 33 1 1 43 * 6% | 22 33 1 1 43 * 6% |
| AlCrMnMoTi Cr ≥ 15% | 22 33 1 1 43 * 3.7% | 22 33 1 1 43 * 3.7% | 22 33 1 1 43 * 6% | 22 33 1 1 43 * 6% |
| AlCrMnMoTi Al + Cr ≥ 15% | 22 33 1 1 43 * 3.7% | 22 33 1 1 43 * 3.7% | 22 33 1 1 43 * 6% | 22 33 1 1 43 * 6% |
| Distance and Boundary Criteria | ||||
|---|---|---|---|---|
| Euclidean Distance | Manhattan Distance | |||
| Boundary_on | Boundary_off | Boundary_on | Boundary_off | |
| Alloy, Constraint | % Al Cr Mn Nb Ti V | |||
| AlCrMnNbTiV 4 elem. ≥ 10% | 17 13 17 1 9 43 * 6.3% | 11 1 9 17 13 49 17 11 17 1 9 45 * 5 11 1 13 21 49 * 5 1 11 13 25 45 * 7.5% | 17 13 17 1 9 43 * 12% | 17 11 17 1 9 45 * 16% |
| AlCrMnNbTiV 5 elem. ≥ 10% | 17 13 17 1 11 41 6.3% | 13 13 13 1 11 49 7.5% | 17 13 17 1 11 41 12% | 11 13 13 1 13 49 * 13 1 11 13 13 49 * 12% |
| AlCrMnNbTiV 6 elem. ≥ 10% | - | - | - | - |
| AlCrMoNbTiV 4 elem. ≥ 10% | 11 5 29 1 13 41 * 6.3% | 11 1 1 25 13 49 * 11 5 25 1 13 45 * 6.3% | 11 1 29 5 13 41 * 12% | 11 1 1 25 13 49 * 11 1 25 1 13 49 * 12% |
| AlCrMoNbTiV 5 elem. ≥ 10% | 13 11 17 1 13 45 5.5% | 13 11 17 1 13 45 5.7% | 11 1 17 13 13 45 * 13 13 19 1 13 41 * 13 1 13 17 11 45 * 8% | 11 1 13 13 13 49 * 13 13 17 1 13 43 * 13 11 29 1 17 29 8% |
| AlCrMoNbTiV 6 elem. ≥ 10% | - | - | - | - |
| AlCrFeTiV 4 elem. ≥ 10% | - | - | - | - |
| AlCrFeTiV 5 elem. ≥ 10% | - | - | - | - |
| AlCrMnMoTi 4 elem. ≥ 10% | 16 17 1 17 49 * 1.4% | 16 17 1 17 49 * 1.4% | 16 17 1 17 49 * 2% | 16 17 1 17 49 * 2% |
| AlCrMnMoTi 5 elem. ≥ 10% | - | - | - | - |
| Alloy | Average, All Compos. | Average Over HEA Compos. at 800 K | Average Over Non- HEA Compos. at 800 K | Max. of All Compos. | Max. of HEA Compos. |
|---|---|---|---|---|---|
| AlCrMnNbTiV | 2.42 | 1.27 | 2.46 | 15 | 4 |
| AlCrMoNbTiV | 3.20 | 3.28 | 3.19 | 15 | 6 |
| AlCrFeTiV | 2.42 | 0.43 | 2.42 | 9 | 2 |
| AlCrMnMoTi | 4.21 | 1.68 | 4.21 | 15 | 4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klaver, T.P.C.; Simonovic, D.; Sluiter, M.H.F. Brute Force Composition Scanning with a CALPHAD Database to Find Low Temperature Body Centered Cubic High Entropy Alloys. Entropy 2018, 20, 911. https://doi.org/10.3390/e20120911
Klaver TPC, Simonovic D, Sluiter MHF. Brute Force Composition Scanning with a CALPHAD Database to Find Low Temperature Body Centered Cubic High Entropy Alloys. Entropy. 2018; 20(12):911. https://doi.org/10.3390/e20120911
Chicago/Turabian StyleKlaver, T. P. C., D. Simonovic, and M. H. F. Sluiter. 2018. "Brute Force Composition Scanning with a CALPHAD Database to Find Low Temperature Body Centered Cubic High Entropy Alloys" Entropy 20, no. 12: 911. https://doi.org/10.3390/e20120911
APA StyleKlaver, T. P. C., Simonovic, D., & Sluiter, M. H. F. (2018). Brute Force Composition Scanning with a CALPHAD Database to Find Low Temperature Body Centered Cubic High Entropy Alloys. Entropy, 20(12), 911. https://doi.org/10.3390/e20120911





