Entropy Analysis of 3D Non-Newtonian MHD Nanofluid Flow with Nonlinear Thermal Radiation Past over Exponential Stretched Surface
Abstract
1. Introduction
2. Mathematical Modeling
Skin Friction Coefficient and Local Nusselt and Sherwood Numbers
3. Convergence Analysis
3.1. Homotopic Solutions
3.2. Deformation Problems at Zeroth Order
3.3. The m-th Order Problem
4. Entropy Analysis
5. Results and Discussion
6. Concluding Remarks
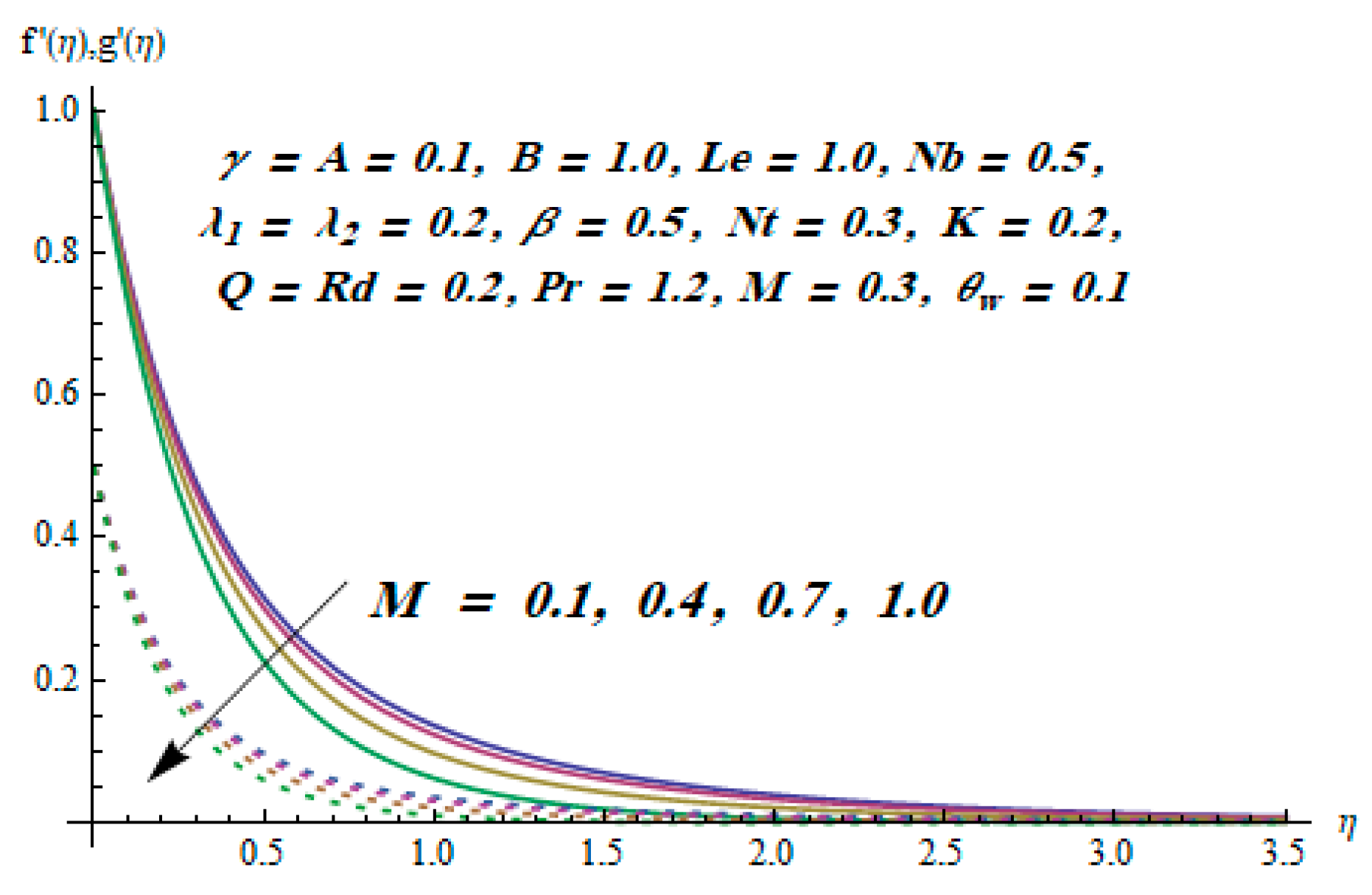
- The velocity components were declining functions of the viscoelastic parameter.
- The temperature field improved with an increase in radiation parameter.
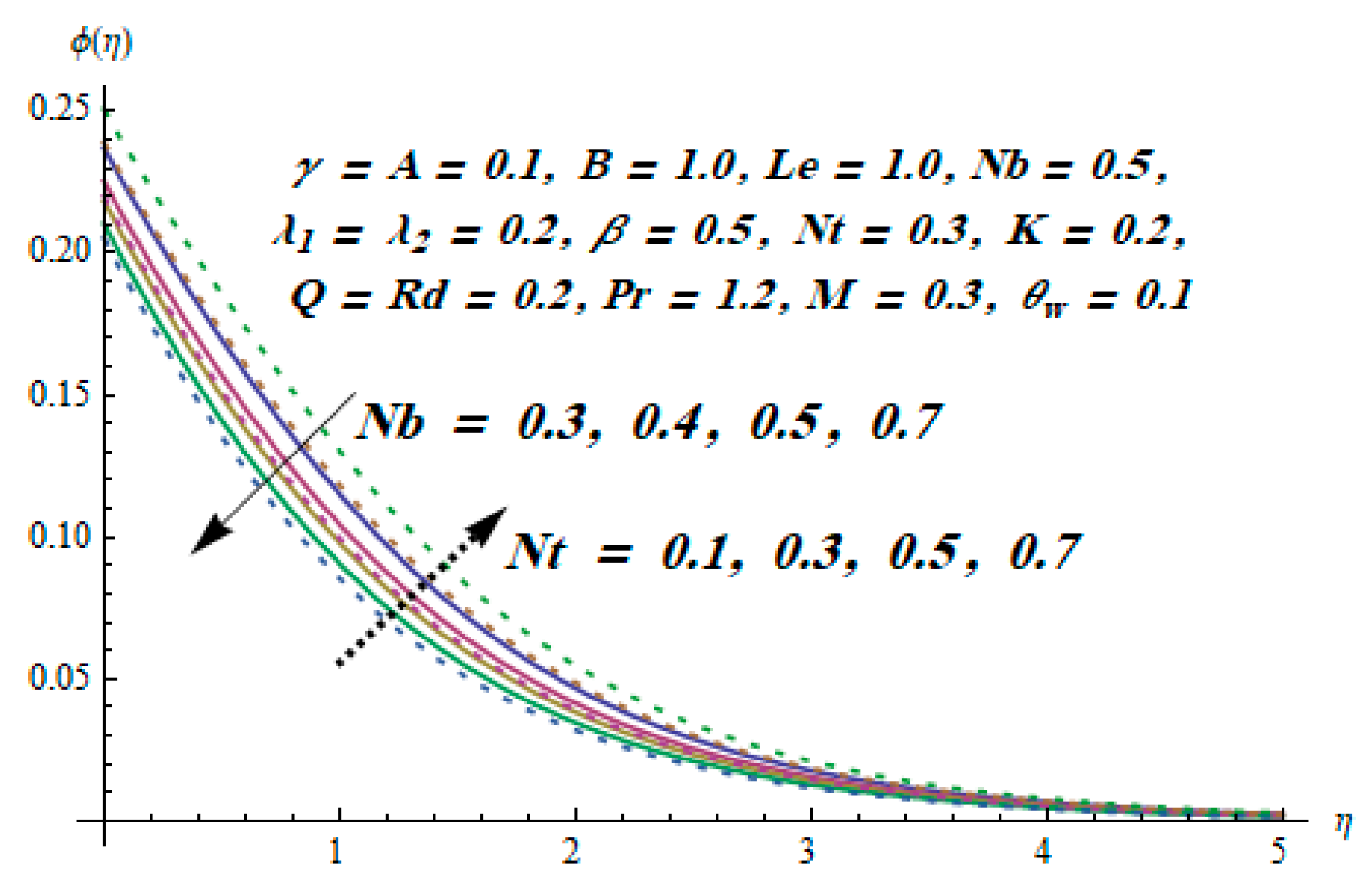
- Thermophoresis and Brownian motion parameters had an opposite effect on concentration distribution.
- With growing values of the magnetic parameter, both velocity components declined.
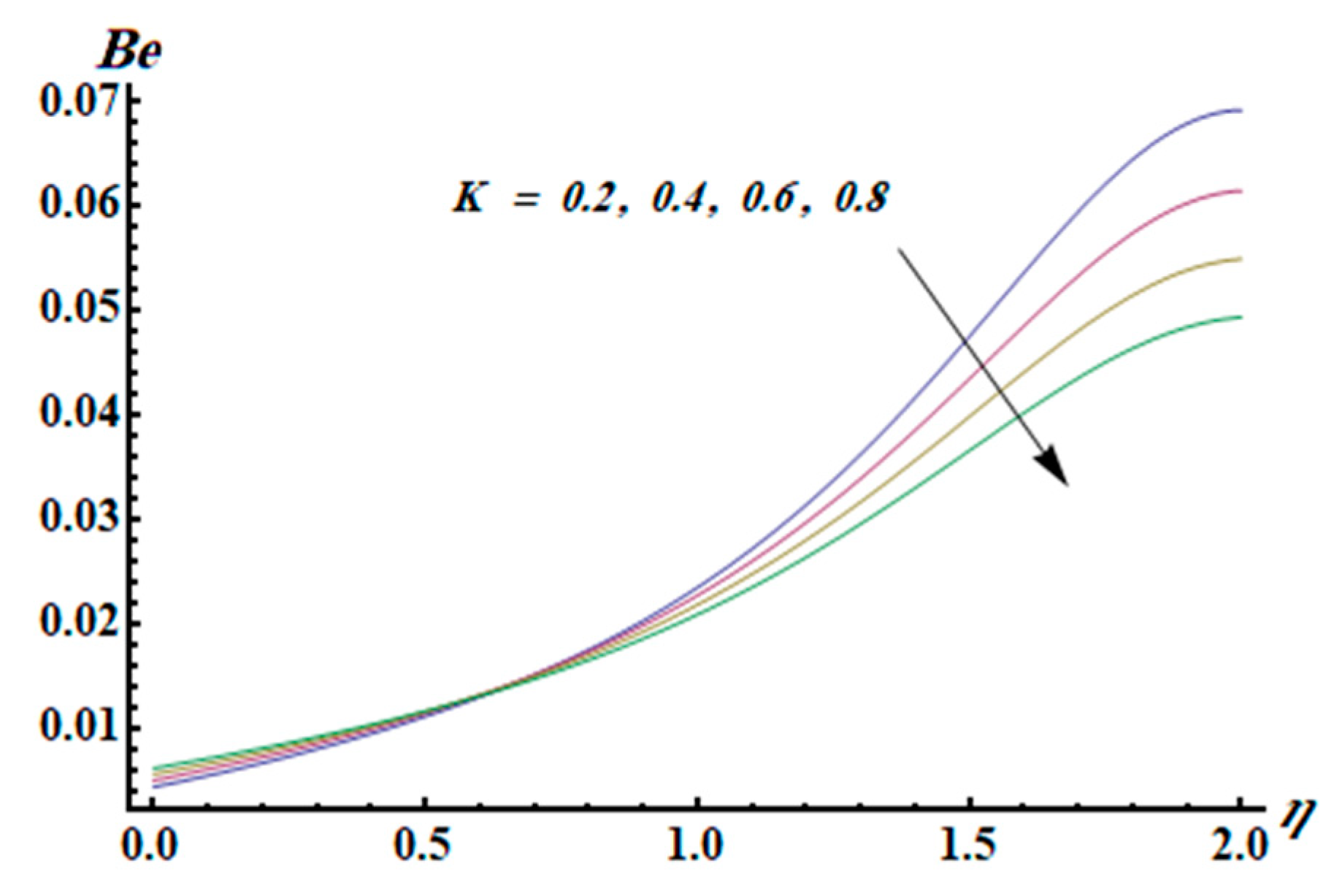
- The Bejan number is an increasing function of the thermal radiation parameter.
- Entropy generation decreased for escalating values of the temperature difference parameter.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| a, b, c, d, e | Dimensional constants |
| η | Similarity variable |
| A | Temperature exponent |
| B | Concentration exponent |
| Be | Bejan number |
| β0 | Magnetic field strength |
| C | Concentration of fluid |
| Cf | Skin friction |
| cp | Specific heat |
| Cw | Concentration on wall |
| C∞ | Ambient concentration |
| C0 | Reference concentration |
| Br | Brinkman number |
| DB | Brownian diffusion coefficient |
| DT | Thermophoretic diffusion coefficient |
| f, g | Dimensionless velocities |
| Effective heat capacity of nanoparticles | |
| k | Thermal conductivity |
| K | Viscoelastic parameter |
| ko | Elastic parameter |
| K* | Mean absorption coefficient |
| α | Effective heat capacity of fluid |
| Le | Lewis number |
| Nb | Brownian motion parameter |
| Nt | Thermophoresis parameter |
| Nux | Nusselt number |
| M | Magnetic parameter |
| Pr | Prandtl number |
| Q | Heat absorption |
| Rd | Thermal radiation parameter |
| Re | Reynolds number |
| SG | Volumetric entropy generation |
| Nux | Local Nusselt number |
| NS | Entropy generation rate |
| Cfx, Cfy | Skin friction coefficients |
| Shx | Sherwood number |
| T | Temperature of fluid |
| Tw | Wall temperature |
| Constants | |
| T∞ | Ambient temperature |
| Ue | Stretching velocity |
| Uw | Linear stretching velocity |
| (u, v, w) | Velocity components |
| (x, y, z) | Coordinate axes |
| M | Hartmann number |
| Kinematic viscosity | |
| λ1 | Relaxation time |
| Λ2 | Ratio of relaxation to retardation time |
| ρ | Density of fluid |
| σ | Electrical conductivity |
| σ* | Stefan–Boltzmann constant |
| μ | Dynamic viscosity |
| τ | Ratio of nanoparticle |
| τw | Skin friction coefficient |
| Ω | Dimensionless temperature difference |
| ε | Dimensionless nanoparticle volume difference |
| Σ | Nanoparticle mass transfer parameter |
| θ | Dimensionless temperature |
| ϕ | Dimensionless concentration |
| α1 | Normal stress moduli |
| Kc | Chemical reaction coefficient |
| Reference length |
References
- Saidur, R.; Leong, K.Y.; Mohammad, H. A review on applications and challenges of nanofluids. Renew. Sustain. Energy Rev. 2011, 15, 1646–1668. [Google Scholar] [CrossRef]
- Xiao, B.; Zhang, X.; Wang, W.; Long, G.; Chen, H.; Kang, H.; Ren, W. A fractal model for water flow through unsaturated porous rocks. Fractals 2018, 26, 1840015. [Google Scholar] [CrossRef]
- Long, G.; Xu, G. The effects of perforation erosion on practical hydraulic-fracturing applications. SPE J. 2017, 22, 645–659. [Google Scholar] [CrossRef]
- Wong, K.V.; De Leon, O. Applications of nanofluids: Current and future. Adv. Mech. Eng. 2010, 2, 519659. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Estman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. ASME-Publications-Fed 1995, 231, 99–106. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Makinde, O.D.; Aziz, A. Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int. J. Therm. Sci. 2011, 50, 1326–1332. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shafee, A.; Ramzan, M.; Li, Z. Investigation of Lorentz forces and radiation impacts on nanofluid treatment in a porous semi annulus via Darcy law. J. Mol. Liquids 2018, 272, 8–14. [Google Scholar] [CrossRef]
- Li, Z.; Sheikholeslami, M.; Shafee, A.; Ramzan, M.; Kandasamy, R.; Al-Mdallal, Q.M. Influence of adding nanoparticles on solidification in a heat storage system considering radiation effect. J. Mol. Liquids 2018, 273, 589–605. [Google Scholar] [CrossRef]
- Muhammad, T.; Lu, D.-C.; Mahanthesh, B.; Eid, M.R.; Ramzan, M.; Dar, A. Significance of Darcy-Forchheimer porous medium in nanofluid through carbon nanotubes. Commun. Theor. Phys. 2018, 70, 361. [Google Scholar] [CrossRef]
- Lu, D.; Ramzan, M.; Ahmad, S.; Chung, J.D.; Farooq, U. A numerical treatment of MHD radiative flow of Micropolar nanofluid with homogeneous-heterogeneous reactions past a nonlinear stretched surface. Sci. Rep. 2018, 8, 12431. [Google Scholar] [CrossRef]
- Ramzan, M.; Ullah, N.; Chung, J.D.; Lu, D.; Farooq, U. Buoyancy effects on the radiative magneto Micropolar nanofluid flow with double stratification, activation energy and binary chemical reaction. Sci. Rep. 2017, 7, 12901. [Google Scholar] [CrossRef]
- Lu, D.C.; Farooq, U.; Hayat, T.; Rashidi, M.M.; Ramzan, M. Computational analysis of three-layer fluid model including a nanomaterial layer. Int. J. Heat Mass Transf. 2018, 122, 222–228. [Google Scholar] [CrossRef]
- Li, Z.; Ramzan, M.; Shafee, A.; Saleem, S.; Al-Mdallal, Q.M.; Chamkha, A.J. Numerical approach for nanofluid transportation due to electric force in a porous enclosure. Microsyst. Technol. 2018, 1–14. [Google Scholar] [CrossRef]
- Liang, M.; Liu, Y.; Xiao, B.; Yang, S.; Wang, Z.; Han, H. An analytical model for the transverse permeability of gas diffusion layer with electrical double layer effects in proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2018, 43, 17880–17888. [Google Scholar] [CrossRef]
- Zhang, D.; Shen, Y.; Zhou, Z.; Qu, J.; Zhou, L.; Wang, J.; Zhang, F. Convection Heat Transfer Performance of Fractal Tube Bank under cross flow. Fractals 2018. [Google Scholar] [CrossRef]
- Xiao, B.; Chen, H.; Xiao, S.; Cai, J. Research on relative permeability of nanofibers with capillary pressure effect by means of fractal-monte carlo technique. J. Nanosci. Nanotechnol. 2017, 17, 6811–6817. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Numerical investigation for CuO-H2O nanofluid flow in a porous channel with magnetic field using mesoscopic method. J. Mol. Liquids 2018, 249, 739–746. [Google Scholar] [CrossRef]
- Lu, D.; Ramzan, M.; ul Huda, N.; Chung, J.D.; Farooq, U. Nonlinear radiation effect on MHD Carreau nanofluid flow over a radially stretching surface with zero mass flux at the surface. Sci. Rep. 2018, 8, 3709. [Google Scholar] [CrossRef]
- Dogonchi, A.S.; Ganji, D.D. Impact of Cattaneo–Christov heat flux on MHD nanofluid flow and heat transfer between parallel plates considering thermal radiation effect. J. Taiwan Inst. Chem. Eng. 2017, 80, 52–63. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Lattice Boltzmann method simulation for MHD non-Darcy nanofluid free convection. Phys. B Condens. Matter 2017, 516, 55–71. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M.; Chung, J.D.; Mann, A.B. On MHD radiative Jeffery nanofluid flow with convective heat and mass boundary conditions. Neural Comput. Appl. 2017, 30, 2739–2748. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M.; Chung, J.D.; Lu, D.C.; Farooq, U. Impact of generalized Fourier’s and Fick’s laws on MHD 3D second grade nanofluid flow with variable thermal conductivity and convective heat and mass conditions. Phys. Fluids 2017, 29, 093102. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M.; Chung, J.D. MHD stagnation point Cattaneo–Christov heat flux in Williamson fluid flow with homogeneous–heterogeneous reactions and convective boundary condition—A numerical approach. J. Mol. Liquids 2017, 225, 856–862. [Google Scholar] [CrossRef]
- Ramzan, M.; Chung, J.D.; Ullah, N. Partial slip effect in the flow of MHD micropolar nanofluid flow due to a rotating disk—A numerical approach. Res. Phys. 2017, 7, 3557–3566. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M.; Chung, J.D. Effects of thermal and solutal stratification on Jeffrey magneto-nanofluid along an inclined stretching cylinder with thermal radiation and heat generation/absorption. Int. J. Mech. Sci. 2017, 131, 317–324. [Google Scholar] [CrossRef]
- Bejan, A. A study of entropy generation in fundamental convective heat transfer. J. Heat Transf. 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Reveillere, A.; Baytas, A.C. Minimum entropy generation for laminar boundary layer flow over a permeable plate. Int. J. Exergy 2010, 7, 164–177. [Google Scholar] [CrossRef]
- López, A.; Ibáñez, G.; Pantoja, J.; Moreira, J.; Lastres, O. Entropy generation analysis of MHD nanofluid flow in a porous vertical microchannel with nonlinear thermal radiation, slip flow and convective-radiative boundary conditions. Int. J. Heat Mass Transf. 2017, 107, 982–994. [Google Scholar] [CrossRef]
- Sheikholeslami, M. New computational approach for exergy and entropy analysis of nanofluid under the impact of Lorentz force through a porous media. Comput. Methods Appl. Mech. Eng. 2018, 344, 319–333. [Google Scholar] [CrossRef]
- Bondareva, N.S.; Sheremet, M.A.; Oztop, H.F.; Abu-Hamdeh, N. Entropy generation due to natural convection of a nanofluid in a partially open triangular cavity. Adv. Powder Technol. 2017, 28, 244–255. [Google Scholar] [CrossRef]
- Sheremet, M.; Pop, I.; Öztop, H.F.; Abu-Hamdeh, N. Natural convection of nanofluid inside a wavy cavity with a non-uniform heating: Entropy generation analysis. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 958–980. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Grosan, T.; Pop, I. Natural convection and entropy generation in a square cavity with variable temperature side walls filled with a nanofluid: Buongiorno’s mathematical model. Entropy 2017, 19, 337. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Sheikholeslami, M.; Zeeshan, A. Entropy analysis on electro-kinetically modulated peristaltic propulsion of magnetized nanofluid flow through a microchannel. Entropy 2017, 19, 481. [Google Scholar] [CrossRef]
- Farooq, U.; Afridi, M.; Qasim, M.; Lu, D. Transpiration and Viscous Dissipation Effects on Entropy Generation in Hybrid Nanofluid Flow over a Nonlinear Radially Stretching Disk. Entropy 2018, 20, 668. [Google Scholar] [CrossRef]
- Hayat, T.; Aziz, A.; Muhammad, T.; Alsaedi, A. Model and comparative study for flow of viscoelastic nanofluids with Cattaneo-Christov double diffusion. PLoS ONE 2017, 12, e0168824. [Google Scholar] [CrossRef]
- Hayat, T.; Ashraf, B.; Shehzad, S.A.; Alsaedi, A.; Bayomi, N. Three-dimensional mixed convection flow of viscoelastic nanofluid over an exponentially stretching surface. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 333–357. [Google Scholar] [CrossRef]
- Farooq, M.; Khan, M.I.; Waqas, M.; Hayat, T.; Alsaedi, A.; Khan, M.I. MHD stagnation point flow of viscoelastic nanofluid with non-linear radiation effects. J. Mol. Liquids 2016, 221, 1097–1103. [Google Scholar] [CrossRef]
- Ramzan, M.; Yousaf, F. Boundary layer flow of three-dimensional viscoelastic nanofluid past a bi-directional stretching sheet with Newtonian heating. AIP Adv. 2015, 5, 057132. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M. Three-dimensional flow of an elastico-viscous nanofluid with chemical reaction and magnetic field effects. J. Mol. Liquids 2016, 215, 212–220. [Google Scholar] [CrossRef]
- Ramzan, M.; Inam, S.; Shehzad, S.A. Three dimensional boundary layer flow of a viscoelastic nanofluid with Soret and Dufour effects. Alex. Eng. J. 2016, 55, 311–319. [Google Scholar] [CrossRef]
- Alsaedi, A.; Hayat, T.; Muhammad, T.; Shehzad, S.A. MHD three-dimensional flow of viscoelastic fluid over an exponentially stretching surface with variable thermal conductivity. Comput. Math. Math. Phy. 2016, 56, 1665–1678. [Google Scholar] [CrossRef]
- Mustafa, M.; Ahmad, R.; Hayat, T.; Alsaedi, A. Rotating flow of viscoelastic fluid with nonlinear thermal radiation: A numerical study. Neural Comput. Appl. 2018, 29, 493–499. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, S.; Shehzad, S.A.; Alsaedi, A. Cattaneo-Christov double-diffusion theory for three-dimensional flow of viscoelastic nanofluid with the effect of heat generation/absorption. Res. Phys. 2018, 8, 489–495. [Google Scholar] [CrossRef]
- Hayat, T.; Shah, F.; Hussain, Z.; Alsaedi, A. Outcomes of double stratification in Darcy–Forchheimer MHD flow of viscoelastic nanofluid. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 145. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; Shafeeurrahman, M. Entropy Generation Due to MHD Mixed Convection of Nanofluid Between Two Concentric Cylinders with Radiation and Joule Heating Effects. J. Nanofluids 2017, 6, 1227–1237. [Google Scholar] [CrossRef]
- Noghrehabadi, A.; Saffarian, M.R.; Pourrajab, R.; Ghalambaz, M. Entropy analysis for nanofluid flow over a stretching sheet in the presence of heat generation/absorption and partial slip. J. Mech. Sci. Technol. 2013, 27, 927–937. [Google Scholar] [CrossRef]
- Abelman, S.; Zaib, A. Entropy generation of nanofluid flow over a convectively heated stretching sheet with stagnation point flow having nimonic 80a nanoparticles: Buongiorno model. In Proceedings of the 13th International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics, Portoroz, Slovenia, 17–19 July 2017. [Google Scholar]
- Shit, G.C.; Haldar, R.; Mandal, S. Entropy generation on MHD flow and convective heat transfer in a porous medium of exponentially stretching surface saturated by nanofluids. Adv. Powder Technol. 2017, 28, 1519–1530. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Determination of the correct range of physical parameters in the approximate analytical solutions of nonlinear equations using the Adomian decomposition method. Mediterr. J. Math. 2016, 13, 4019–4037. [Google Scholar] [CrossRef]
- Liu, I.-C.; Wang, H.-H.; Peng, Y.-F. Flow and heat transfer for three-dimensional flow over an exponentially stretching surface. Chem. Eng. Commun. 2013, 200, 253–268. [Google Scholar] [CrossRef]
















| Order of Approximation | ||||
|---|---|---|---|---|
| 1 | 1.19588 | 0.12037 | 0.16113 | 0.16180 |
| 3 | 1.37115 | 0.13887 | 0.15382 | 0.15745 |
| 7 | 1.42903 | 0.14518 | 0.14911 | 0.15586 |
| 10 | 1.45762 | 0.14852 | 0.14206 | 0.15476 |
| 13 | 1.46000 | 0.14883 | 0.13937 | 0.15471 |
| 14 | 1.46000 | 0.14883 | 0.13798 | 0.15460 |
| 15 | 1.46000 | 0.14883 | 0.13796 | 0.15460 |
| 18 | 1.46000 | 0.14883 | 0.13796 | 0.15460 |
| λ | Nb | Nt | Le | Pr | M | K | Rd | A | Q | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | - | - | - | - | - | - | - | - | - | 0.13878 | 0.12199 |
| 0.2 | - | - | - | - | - | - | - | - | - | 0.1388 | 0.12157 |
| 0.5 | - | - | - | - | - | - | - | - | - | 0.1421 | 0.12032 |
| - | 0.5 | - | - | - | - | - | - | - | - | 0.13878 | 0.12199 |
| - | 1.0 | - | - | - | - | - | - | - | - | 0.13772 | 0.11917 |
| - | 1.5 | - | - | - | - | - | - | - | - | 0.13770 | 0.11823 |
| - | - | 0.0 | - | - | - | - | - | - | - | 0.13878 | 0.11635 |
| - | - | 0.2 | - | - | - | - | - | - | - | 0.13878 | 0.12199 |
| - | - | 0.5 | - | - | - | - | - | - | - | 0.13878 | 0.12576 |
| - | - | - | 1.0 | - | - | - | - | - | - | 0.14447 | 0.12981 |
| - | - | - | 1.5 | - | - | - | - | - | - | 0.13878 | 0.12199 |
| - | - | - | 2.0 | - | - | - | - | - | - | 0.12572 | 0.11010 |
| - | - | - | - | 1.0 | - | - | - | - | - | 0.13878 | 0.12199 |
| - | - | - | - | 1.2 | - | - | - | - | - | 0.13775 | 0.08889 |
| - | - | - | - | 1.5 | - | - | - | - | - | 0.13774 | 0.06499 |
| - | - | - | - | - | 0.0 | - | - | - | - | 0.13878 | 0.12199 |
| - | - | - | - | - | 0.2 | - | - | - | - | 0.13878 | 0.12199 |
| - | - | - | - | - | 0.3 | - | - | - | - | 0.13878 | 0.12199 |
| - | - | - | - | - | - | 0.0 | - | - | - | 0.13878 | 0.12199 |
| - | - | - | - | - | - | 0.02 | - | - | - | 0.13878 | 0.12199 |
| - | - | - | - | - | - | 0.04 | - | - | - | 0.13878 | 0.12199 |
| - | - | - | - | - | - | - | 0.2 | - | - | 0.13878 | 0.12199 |
| - | - | - | - | - | - | - | 0.4 | - | - | 0.14392 | 0.12146 |
| - | - | - | - | - | - | - | 0.5 | - | - | 0.14480 | 0.12123 |
| - | - | - | - | - | - | - | - | 0.1 | - | 0.13878 | 0.12199 |
| - | - | - | - | - | - | - | - | 0.5 | - | 0.13878 | 0.12199 |
| - | - | - | - | - | - | - | - | 0.7 | - | 0.13878 | 0.12199 |
| - | - | - | - | - | - | - | - | - | 0.2 | 0.13878 | 0.12199 |
| - | - | - | - | - | - | - | - | - | 0.4 | 0.14962 | 0.12199 |
| - | - | - | - | - | - | - | - | - | 0.5 | 0.15679 | 0.12199 |
| λ | M | K | ||
|---|---|---|---|---|
| 0.1 | - | - | 1.6768 | 0.2237 |
| 0.2 | - | - | 1.7698 | 0.4089 |
| 0.5 | - | - | 2.0571 | 1.0804 |
| - | 0.3 | - | 1.6768 | 0.2237 |
| - | 0.5 | - | 1.7422 | 0.2325 |
| - | 1.0 | - | 2.0212 | 0.2697 |
| - | - | 0.02 | 1.6768 | 0.2237 |
| - | - | 0.03 | 1.9607 | 0.2675 |
| - | - | 0.04 | 1.8168 | 0.3138 |
| β | Pr | A | Liu et al. [52] | Present Study |
|---|---|---|---|---|
| 0.0 | 0.7 | 0.0 | −0.42583804 | −0.4258120 |
| 2.0 | −1.02143617 | −1.0214514 | ||
| 5.0 | −1.64165922 | −1.6416620 | ||
| 0.25 | 0.7 | 0.0 | −0.47609996 | −0.4761032 |
| 2.0 | −1.14199997 | −1.1420014 | ||
| 5.0 | −1.83543073 | −1.8354210 | ||
| 0.50 | 0.7 | 0.0 | −0.52154103 | −0.5215267 |
| 2.0 | −1.25099820 | −1.2509991 | ||
| 5.0 | −2.01061361 | −2.0106021 | ||
| 0.75 | 0.7 | 0.0 | −0.56332861 | −0.5633148 |
| 2.0 | −1.35123246 | −1.3512221 | ||
| 5.0 | −2.17171091 | −2.1717006 | ||
| 1.0 | 0.7 | 0.0 | −0.60222359 | −0.6022167 |
| 2.0 | −1.44452826 | −1.4445214 | ||
| 5.0 | −2.32165661 | −2.3216340 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suleman, M.; Ramzan, M.; Zulfiqar, M.; Bilal, M.; Shafee, A.; Chung, J.D.; Lu, D.; Farooq, U. Entropy Analysis of 3D Non-Newtonian MHD Nanofluid Flow with Nonlinear Thermal Radiation Past over Exponential Stretched Surface. Entropy 2018, 20, 930. https://doi.org/10.3390/e20120930
Suleman M, Ramzan M, Zulfiqar M, Bilal M, Shafee A, Chung JD, Lu D, Farooq U. Entropy Analysis of 3D Non-Newtonian MHD Nanofluid Flow with Nonlinear Thermal Radiation Past over Exponential Stretched Surface. Entropy. 2018; 20(12):930. https://doi.org/10.3390/e20120930
Chicago/Turabian StyleSuleman, Muhammad, Muhammad Ramzan, Madiha Zulfiqar, Muhammad Bilal, Ahmad Shafee, Jae Dong Chung, Dianchen Lu, and Umer Farooq. 2018. "Entropy Analysis of 3D Non-Newtonian MHD Nanofluid Flow with Nonlinear Thermal Radiation Past over Exponential Stretched Surface" Entropy 20, no. 12: 930. https://doi.org/10.3390/e20120930
APA StyleSuleman, M., Ramzan, M., Zulfiqar, M., Bilal, M., Shafee, A., Chung, J. D., Lu, D., & Farooq, U. (2018). Entropy Analysis of 3D Non-Newtonian MHD Nanofluid Flow with Nonlinear Thermal Radiation Past over Exponential Stretched Surface. Entropy, 20(12), 930. https://doi.org/10.3390/e20120930






