2. Informational Indexes of Strings
Given a string over an alphabet A of m symbols, then we denote by the set of all substrings of and by the set of k-mers of , that is, the strings of of length k. The function gives the number of occurrences of substring in . Two important classes of k-mers are repeats and hapaxes. The k-mer is a repeat of if , whereas is a hapax of if (the word hapax comes from the Greek root meaning once). In other words, hapaxes are unrepeatable substrings of .
If is a repeat of , then every substring of is a repeat of as well. Analogously, if is a hapax of , then every string including as a substring is a hapax of as well.
In terms of repeats and hapaxes, we can define the following indexes that we call informational indexes because they are associated with a string viewed as the information source in the sense of Shannon’s information theory. These indexes are very useful in understanding the internal structure of strings.
The index:
(maximum repeat length) is the length of the longest repeats occurring in
, while:
(minimum hapax length) is the length of the shortest hapaxes occurring in
. Moreover,
(maximum complete length) is the maximum length
k such that all possible
k-mers occur in
. A straightforward, but inefficient computation of such indexes can be performed in accordance with their mathematical formulation, but more sophisticated manners were implemented in [
28] by exploiting suitable indexing data structures.
Indexes
and
, called logarithmic length and double logarithmic length, are defined by the following equations, where
denotes the length of string
(
m is the number of different symbols occurring in
):
When is given by the context, we simply write: , instead of , respectively. The following propositions follow immediately from the definitions above.
Proposition 1. For , all k-mer of α are hapaxes.
Proposition 2. For , all k-mer of α are repeats.
Proposition 3. For any string α, .
Proposition 4. For any string α of length n: , and if , then all the elements of are hapaxes of α.
Proposition 5. In any string, the following inequality holds: The notation refers to the ceiling function, namely the smallest integer following the value .
By using
, we can define probability distributions over
, by setting
. The empirical
k-entropy of the string
is given by Shannon’s entropy with respect to the distribution
p of
k-mers occurring in
(we use the logarithm in base
m for uniformity with the following discussion):
It is well known [
11] that entropy reaches its maximum for uniform probability distributions. Therefore, when all the
k-mers of a string
of length
n occur with the uniform probability
, this means that the following proposition holds.
Proposition 6. If all k-mers of α are hapaxes, then reaches its maximum value in the set of probability distributions over .
3. A “Positive” Notion of a Random String
It is not easy to tell when a string is a random string, but it is easy to decide when a given string is not a true random string. A “negative” approach to string randomness could be based on a number of conditions , each of which implies non-randomness. In this way, when a string does not satisfy any such conditions, we have a good guarantee of its randomness. In a sense, mathematical characterizations of randomness are “negative” definitions based on infinite sets of conditions. Therefore, even if these sets are recursively enumerable, randomness cannot be effectively stated.
Now, we formulate a principle that is a sort of Borel normality principle for finite strings. It expresses a general aspect of any reasonable definition of randomness. In informal terms, this principle says that any substring has the same probability of occurring in a random string, and for the substring under a given length, the knowledge of any prefix of a random string does not give any information about their occurrence in the remaining part of the string. In this sense, a random string is a global structure where no partial knowledge is informative about the whole structure.
Principle 1 (Random Log Normality Principle (RLNP)).
In any finite random string α, of length n over m symbols, for any value of , all possible k-mers have the same a priori probability of occurring at each position i, for . Moreover, let us define the a posteriori probability that a k-mer occurs at position i as the conditional probability of occurring when the prefix of is given. Then, for any , at each position i of α, for , the a posteriori probability of any k-mer occurrence has to remain the same as its a priori probability. □
The reader may wonder about the choice of the bound that appears in the RLNP principle stated above. It is motivated by Proposition 7, which is proven by using the first part of the RLNP principle.
In the following, a string is considered to be random if it satisfies the RLNP principle. Let us denote by
the set of random strings of length
n over
m symbols and by
the union of
for
:
For individual strings, in general, RLNP can hold only admitting some degree of deviance from the theoretical pure case. This means that the randomness of an individual string cannot be assessed as a 0/1 property, but rather, in terms of some measure expressing the closeness to the ideal cases (for example, the percentage of positions where RLNP fails).
According to this perspective, RLNP may not exactly hold in the whole set . Nevertheless, the subset of on which RLNP fails has to approximate to the empty set, or better, to a set of zero measure, as n increases. In other words, random strings are “ideal” strings by means of which the degree of similarity to them can be considered as a “degree of membership” of individual strings to RND. This lack of precision is the price to pay for having a “positive” characterization of string randomness.
The following proposition states an inferior length bound for the hapaxes of a random string.
Proposition 7. For any , if:then all k-mers of α are hapaxes of α. Proof. Let us consider a length
k such that:
According to RLNP, the probability that a
k-mer occurs in
is given by the following ratio (the number of available positions of
k-mers is
:
but, if all
k-mers are hapaxes in
, then their probability of occurring in
is also given by:
Then, if we equate the right members of the two equations above (
1) and (
2), we obtain an equation that has to be satisfied by any length
k, ensuring that all
k-mers occurring in
are hapaxes in
:
which implies:
In order to evaluate the values of
k, we solve the equation above by replacing
k in the left member of Equation (
4) by the whole left member of Equation (
4):
Now, Equation (
5) implies that:
However, the difference between the two bounds of
k is given by:
where the right member approximates to zero as
n increases. In conclusion:
This means that for:
all
k-mers of
are hapaxes, that is,
is a lower bound for all unrepeatable substrings of
. □
The following proposition follows as a direct consequence of the previous proposition and Proposition 1.
In conclusion, we have shown that in random strings, is strictly related to the index.
According to the proposition above, the index has a clear entropic interpretation: it is the value of k such that the empirical entropy of a random string reaches its maximum value.
We have seen that in random strings, all substrings longer than are unrepeatable, but what about the minimum length of unrepeatable substrings? The following proposition answers this question, by stating an upper bound for the length of repeats in random strings.
Proof. Let us consider . If some of such k-mers is a hapax, the proposition is proven. Otherwise, if no k-mer is a hapax of , then all k-mers of are repeats. However, this fact is against the Random Log Normality Principle (RLNP). Namely, in all the positions i of such that in , a k-mer occurs once (these positions necessarily exist), the a posteriori probability that has of occurring in a position of after is , surely greater than (where ). Hence, in positions after i, the a posteriori probability would be different from the a priori probability. In conclusion, if , some hapaxes of length have to occur in ; thus, necessarily, . □
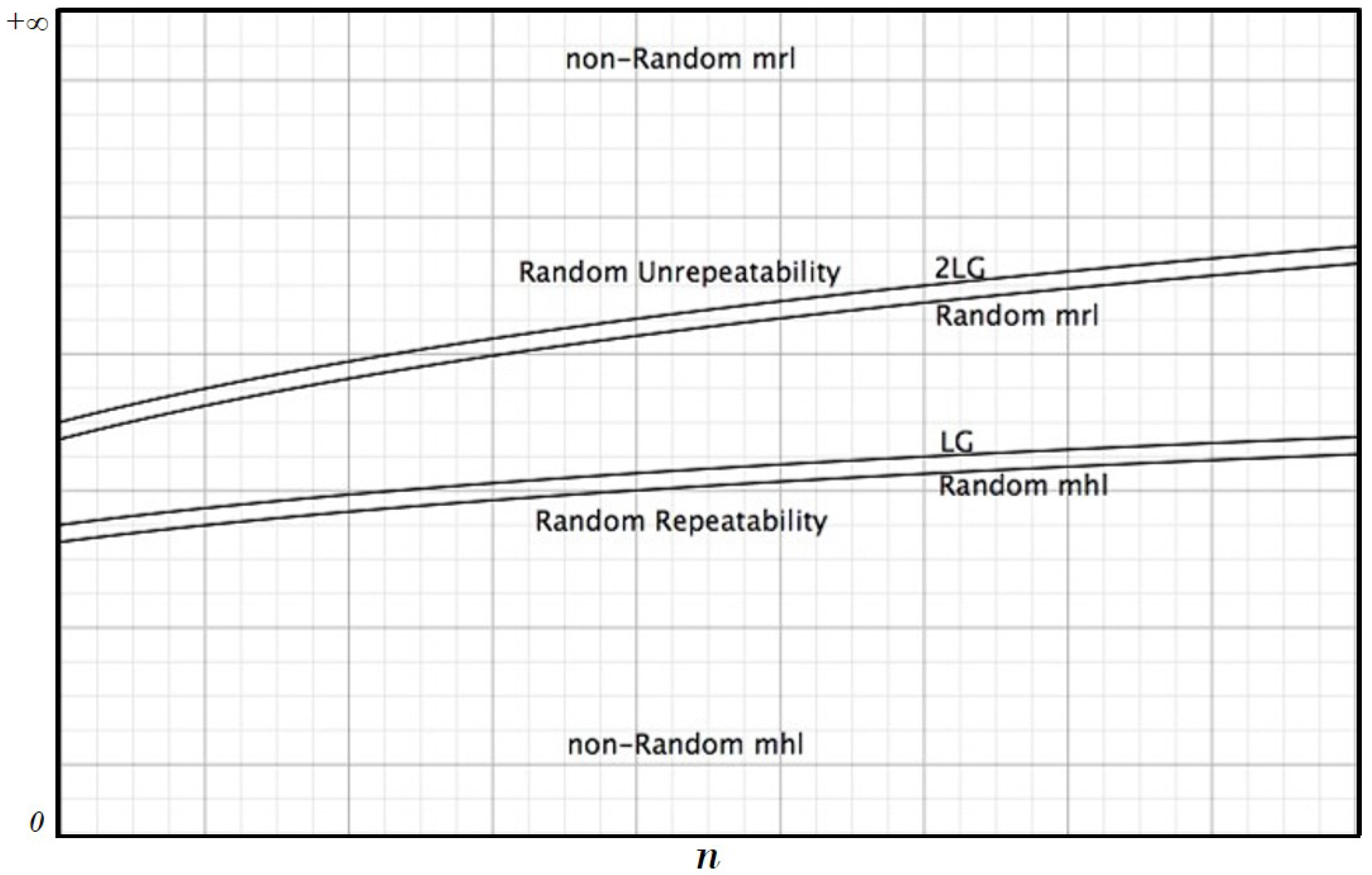
Our analysis shows that in random strings, there are two bounds given by
and
(
Figure 1). Under the first one, we have only repeatable sub-strings, while over the second one, we have only unrepeatable sub-strings. The agreement with these conditions and the degrees of deviance from them give an indication about the randomness degree of a given string.
It is easy to provide examples of strings where these conditions are not satisfied, but what is interesting to remark is that the conditions hold with a very strict approximation for strings that pass the usual randomness statistical tests; moreover, for “long strings”, such as genomes, the bounds hold, but in a very sloppy way because usually is considerably greater than and is considerably smaller that .
In our findings reported in
Section 5, the best randomness was found for strings of
decimal digits, for quantum measurements, and for strings obtained by pseudo-casual generators [
29]. In the next sections, we discuss our experimental data about our randomness parameters.
4. Log Bounds Randomness Test
The Log Bounds Test (LBT), based on the analysis developed in the previous sections, essentially checks, for a given string, the logarithmic bounds for its prefixes and in the average (with the standard deviation). We apply LBT to a wide class of strings, in order to verify if it correctly guesses the randomness of strings traditionally judged random and, at the same time, if it does not give such evidence in the cases where it is not appropriate. The results confirm a discrimination capability with a complete accordance with our expectations.
For our analyses, we have taken into account different types of strings that are commonly considered as random strings, available in public archives accessed on June 2018.
Quantum physics-generated data based on the non-determinism of photon arrival times provide up to 150 Mbits/s in the form of a series of bytes, available at
http://qrng.physik.hu-berlin.de/.
Another category of random data is given by mathematical functions that provide chaotic dynamics, such as the logistic map with the parameter in .
Linear congruential generators of the form
generate pseudo-random numbers [
17,
18] that we converted into strings of suitable alphabets of different sizes by applying discretization mechanisms.
Another category is given by random series related to roulette spins, cards, dice, and Bernoulli urns. In particular, we took into account three million consecutive roulette spins produced by the Spielbank Wiesbaden casino, at the website
https://www.roulette30.com/2014/11/free-spins-download.html. As was already recognized by several authors, the randomness of roulette data is not true randomness, and this was also confirmed by our findings.
For comparisons, we used non-random data given by the complete works of Shakespeare available at
http://norvig.com/ngrams/shakespeare.txt. These texts were transformed in order to extract from them only letters by discarding other symbols.
We used another comparison text given by the complete genome of the
Sorangium cellulosum bacterium, downloaded from the RefSeq/NCBI database at
https://www.ncbi.nlm.nih.gov/nuccore/NC_010162.1 (with a length of around 13 million nucleotides).
5. Analysis of the Experimental Results
When the informational indexes
and
result in coinciding with
and
, respectively, we consider this coincidence as a positive symptom of randomness, and we will mark this fact by writing ✓ on the right of the compared values (or ✗ in the opposite case). The more these coincidences are found for prefixes of a string, the more the string passes our test (a more precise evaluation could consider not only the number of coincidence, but also how much the values differ, when they do not coincide). As the tables in the next section show, our findings agree, in a very significant way, with the usual randomness/non-randomness expectations. The tables are given for different categories of strings. Informational indexes were computed by a specific platform for long string analysis [
28]. In
Table 1, from 100,000 up to 30 million decimal expansions of
are considered. The agreement with our theory is almost complete, whence a very high level of randomness is confirmed, with only a very slight deviance.
Other tables are relative to decimal expansions of other real numbers:
Table 2 for Euler’s constant,
Table 3 for
, and
Table 4 for Champernowne’s constant, a real transcendent number obtained by a non-periodic infinite sequence of decimal digits (the concatenated decimal representations of all natural numbers in their increasing order). It is interesting to observe that Euler’s constant and
have behaviors similar to
, whereas Champernowne’s constant has values indicating an inferior level of randomness.
Table 5 concerns strings coming from the pseudo-casual Java generator (a linear congruential generator). The randomness of these data, with respect to our indexes, is very good.
Table 6 is relative to strings generated via the logistic map. In these cases, randomness is not so clearly apparent, due to a sort of tendency to have patterns of a periodic nature, which agree with the already recognized behaviors due to the limits of computer number representations [
30].
Table 7 provides our indexes for quantum data [
29], by showing a perfect agreement with a random profile.
Table 8 is relative to three millions of roulette spins, with an almost complete failure of the 2LG-check (even if with a quite limited gap).
Finally,
Table 9 and
Table 10 are relative to a DNA bacterial genome and to texts of natural language (Shakespeare’s works), respectively. In these cases, as expected, our indexes of randomness reveal low levels of randomness.
6. Conclusions
In this paper, we presented an approach to randomness that extends previous results on informational genomics (information theory applied to the analyses of genomes [
27]), where the analysis of random genomes was used for defining genome evolutionary complexity [
26], and a method for choosing the appropriate k-mer length for discovering sequence similarity in the context of homology relationship between genomes [
25]. A general analysis of randomness has emerged that suggests a line of investigation where a theoretical approach is coupled with a practical and experimental viewpoint, as required by the application of randomness to particular situations of interest. Randomness has an intrinsic paradoxical, and at the same time vague, nature. In fact, mathematically-rigorous definitions of randomness are intrinsically uncomputable, and algorithmically-testable properties are not exhaustive.
We introduced the random log normality principle, which resembles Borel’s normality [
17], but it is formulated, for finite strings, in terms of a priori and a posteriori probabilities. This principle allows us to define two logarithmic bounds that state precise links between the length of strings and the lengths to which specific phenomena of substring repetitiveness must or cannot hold.
A possible continuation of our investigation could be addressed to extend similar principles and tests for finite structures, such as trees or graphs. In fact, in many applications, it would be very useful to have reliable and simple tests for finite mathematical structures commonly used in data representations.