Effect of Atomic Size Difference on the Microstructure and Mechanical Properties of High-Entropy Alloys
Abstract
:1. Introduction
2. Materials and Experimental Methods
3. Results
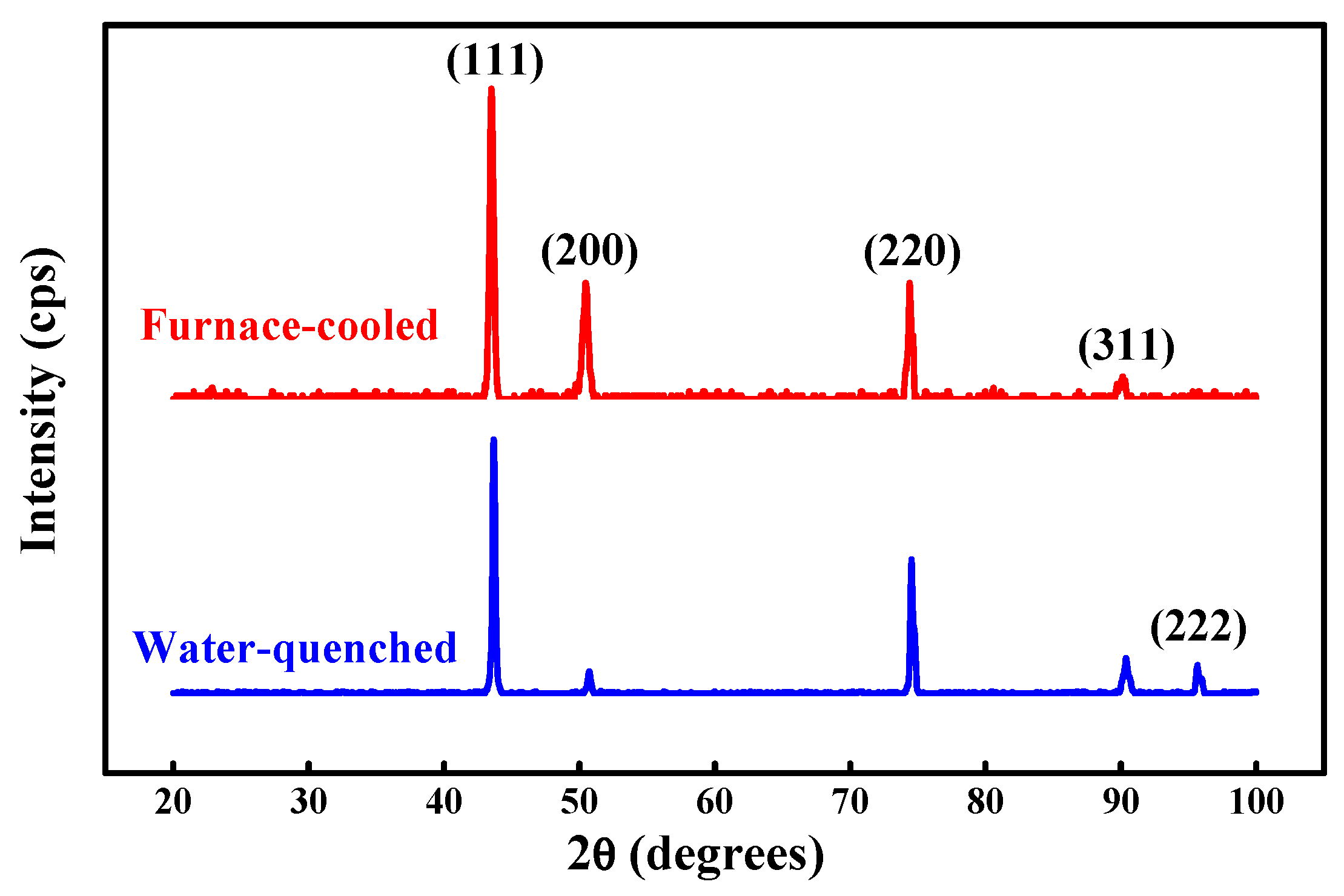
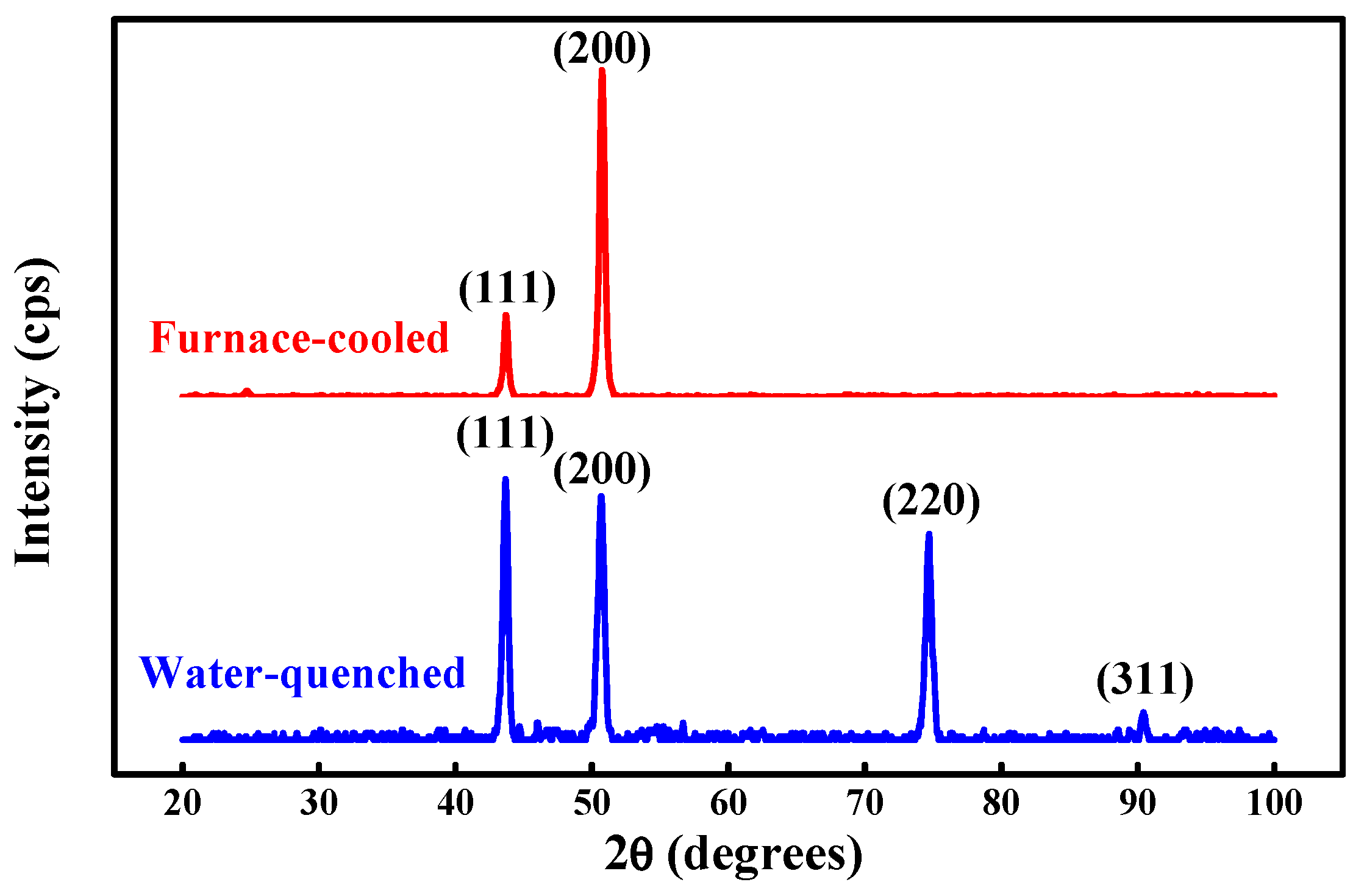
3.1. Microstructure and Crystalline Structure
3.2. Grain Growth Activation Energy of Al0.2CoCrFeMnNi and Al0.3CoCrCu0.3FeNi Alloys
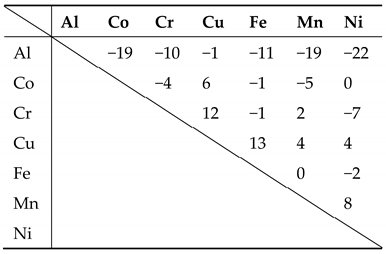
3.3. Relationship between Atomic Size Difference and Grain Growth Activation Energy
4. Discussion
4.1. Effect of Atomic Size Difference on Microstructures
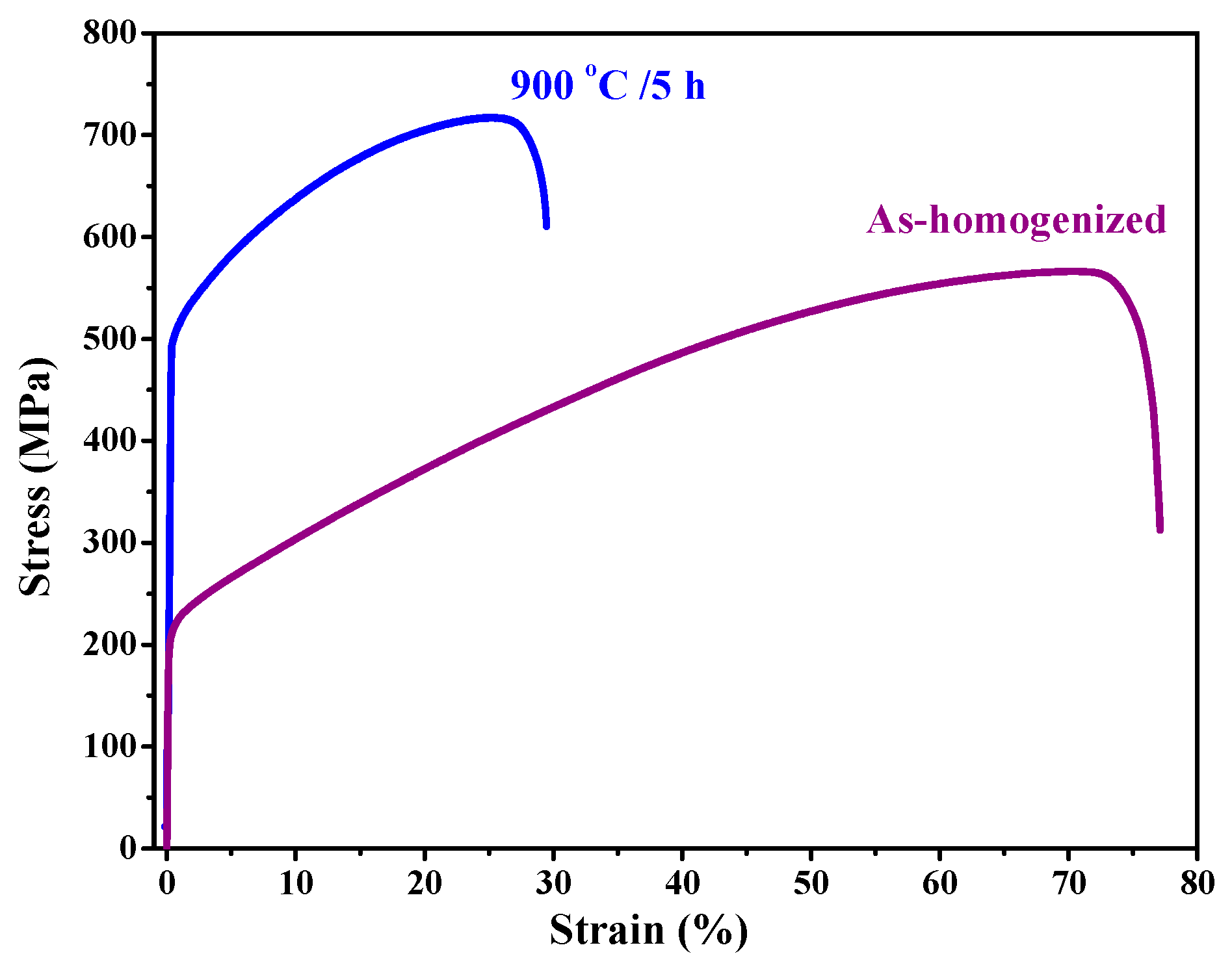
4.2. Effect of Atomic Size Difference on Mechanical Properties
4.3. Comparison of Tensile Properties with Different HEAs
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yeh, J.W.; Chen, S.K.; Lin, S.J.; Gan, J.Y.; Chin, T.S.; Shun, T.T.; Tsau, C.H.; Chang, S.Y. Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Cantor, B.; Chang, I.T.H.; Knight, P.; Vincent, A.J.B. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2004, 375, 213–218. [Google Scholar] [CrossRef]
- Yeh, J.-W. Recent progress in high-entropy alloys. Ann. Chim. Sci. Matér. 2006, 31, 633–648. [Google Scholar] [CrossRef]
- Yeh, J.W.; Chen, S.K.; Gan, J.Y.; Lin, S.J.; Chin, T.S.; Shun, T.T.; Tsau, C.H.; Chang, S.Y. Formation of simple crystal structures in Cu-Co-Ni-Cr-Al-Fe-Ti-V alloys with multiprincipal metallic elements. Metall. Mater. Trans. A-Phys. Metall. Mater. Sci. 2004, 35A, 2533–2536. [Google Scholar] [CrossRef]
- Tsai, K.Y.; Tsai, M.H.; Yeh, J.W. Sluggish diffusion in Co-Cr-Fe-Mn-Ni high-entropy alloys. Acta Mater. 2013, 61, 4887–4897. [Google Scholar] [CrossRef]
- Otto, F.; Hanold, N.L.; George, E.P. Microstructural evolution after thermomechanical processing in an equiatomic, single-phase cocrfemnni high-entropy alloy with special focus on twin boundaries. Intermetallics 2014, 54, 39–48. [Google Scholar] [CrossRef]
- Otto, F.; Dlouhý, A.; Somsen, C.; Bei, H.; Eggeler, G.; George, E.P. The influences of temperature and microstructure on the tensile properties of a cocrfemnni high-entropy alloy. Acta Mater. 2013, 61, 5743–5755. [Google Scholar] [CrossRef]
- Gludovatz, B.; Hohenwarter, A.; Catoor, D.; Chang, E.H.; George, E.P.; Ritchie, R.O. A fracture-resistant high-entropy alloy for cryogenic applications. Science 2014, 345, 1153–1158. [Google Scholar] [CrossRef] [Green Version]
- He, J.Y.; Liu, W.H.; Wang, H.; Wu, Y.; Liu, X.J.; Nieh, T.G.; Lu, Z.P. Effects of al addition on structural evolution and tensile properties of the feconicrmn high-entropy alloy system. Acta Mater. 2014, 62, 105–113. [Google Scholar] [CrossRef]
- Wu, Z.; Bei, H.; Pharr, G.M.; George, E.P. Temperature dependence of the mechanical properties of equiatomic solid solution alloys with face-centered cubic crystal structures. Acta Mater. 2014, 81, 428–441. [Google Scholar] [CrossRef]
- Zaddach, A.J.; Scattergood, R.O.; Koch, C.C. Tensile properties of low-stacking fault energy high-entropy alloys. Mater. Sci. Eng. A 2015, 636, 373–378. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Y.J.; Lin, J.P.; Chen, G.L.; Liaw, P.K. Solid-solution phase formation rules for multi-component alloys. Adv. Eng. Mater. 2008, 10, 534–538. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y. Prediction of high-entropy stabilized solid-solution in multi-component alloys. Mater. Chem. Phys. 2012, 132, 233–238. [Google Scholar] [CrossRef]
- Guo, S.; Liu, C.T. Phase stability in high entropy alloys: Formation of solid-solution phase or amorphous phase. Prog. Nat. Sci. 2011, 21, 433–446. [Google Scholar] [CrossRef]
- Lee, C.; Song, G.; Gao, M.C.; Feng, R.; Chen, P.; Brechtl, J.; Chen, Y.; An, K.; Guo, W.; Poplawsky, J.D. Lattice distortion in a strong and ductile refractory high-entropy alloy. Acta Mater. 2018, 160, 158–172. [Google Scholar] [CrossRef]
- Lubarda, V. On the effective lattice parameter of binary alloys. Mech. Mater. 2003, 35, 53–68. [Google Scholar] [CrossRef]
- Owen, L.R.; Jones, N.G. Lattice distortions in high-entropy alloys. J. Mater. Res. 2018, 33, 2954–2969. [Google Scholar] [CrossRef]
- Tang, Z.; Gao, M.C.; Diao, H.; Yang, T.; Liu, J.; Zuo, T.; Zhang, Y.; Lu, Z.; Cheng, Y.; Zhang, Y.; et al. Aluminum alloying effects on lattice types, microstructures, and mechanical behavior of high-entropy alloys systems. Jom 2013, 65, 1848–1858. [Google Scholar] [CrossRef]
- Tung, C.-C.; Yeh, J.-W.; Shun, T.-T.; Chen, S.-K.; Huang, Y.-S.; Chen, H.-C. On the elemental effect of alcocrcufeni high-entropy alloy system. Mater. Lett. 2007, 61, 1–5. [Google Scholar] [CrossRef]
- Tsai, C.-W.; Chen, Y.-L.; Tsai, M.-H.; Yeh, J.-W.; Shun, T.-T.; Chen, S.-K. Deformation and annealing behaviors of high-entropy alloy Al0.5CoCrCuFeNi. J. Alloys Compd. 2009, 486, 427–435. [Google Scholar] [CrossRef]
- Tsai, C.-W.; Tsai, M.-H.; Yeh, J.-W.; Yang, C.-C. Effect of temperature on mechanical properties of al0.5cocrcufeni wrought alloy. J. Alloys Compd. 2010, 490, 160–165. [Google Scholar] [CrossRef]
- Sheng, H.F.; Gong, M.; Peng, L.M. Microstructural characterization and mechanical properties of an al0.5cocrfecuni high-entropy alloy in as-cast and heat-treated/quenched conditions. Mater. Sci. Eng. A 2013, 567, 14–20. [Google Scholar] [CrossRef]
- Tong, C.J.; Chen, M.R.; Chen, S.K.; Yeh, J.W.; Shun, T.T.; Lin, S.J.; Chang, S.Y. Mechanical performance of the alxcocrcufeni high-entropy alloy system with multiprincipal elements. Metall. Mater. Trans. A-Phys. Metall. Mater. Sci. 2005, 36A, 1263–1271. [Google Scholar] [CrossRef]
- Hume-Rothery, W. Atomic Theory for Students of Metallurgy; Institute of Metals: London, UK, 1952. [Google Scholar]
- Guo, S.; Ng, C.; Lu, J.; Liu, C. Effect of valence electron concentration on stability of fcc or bcc phase in high entropy alloys. J. Appl. Phys. 2011, 109, 103505. [Google Scholar] [CrossRef] [Green Version]
- Tian, F.; Varga, L.K.; Chen, N.; Shen, J.; Vitos, L. Empirical design of single phase high-entropy alloys with high hardness. Intermetallics 2015, 58, 1–6. [Google Scholar] [CrossRef]
- Haas, S.; Mosbacher, M.; Senkov, O.; Feuerbacher, M.; Freudenberger, J.; Gezgin, S.; Völkl, R.; Glatzel, U. Entropy determination of single-phase high entropy alloys with different crystal structures over a wide temperature range. Entropy 2018, 20, 654. [Google Scholar] [CrossRef]
- Huang, P.K.; Yeh, J.W. Inhibition of grain coarsening up to 1000 degrees C in (AlCrNbSiTiV)N superhard coatings. Scr. Mater. 2010, 62, 105–108. [Google Scholar] [CrossRef]
- Zhu, C.; Lu, Z.; Nieh, T. Incipient plasticity and dislocation nucleation of fecocrnimn high-entropy alloy. Acta Mater. 2013, 61, 2993–3001. [Google Scholar] [CrossRef]
- Basu, I.; Ocelík, V.; De Hosson, J.T.M. Size effects on plasticity in high-entropy alloys. J. Mater. Res. 2018, 33, 3055–3076. [Google Scholar] [CrossRef]
- Song, H.; Tian, F.; Hu, Q.-M.; Vitos, L.; Wang, Y.; Shen, J.; Chen, N. Local lattice distortion in high-entropy alloys. Phys. Rev. Mater. 2017, 1, 023404. [Google Scholar] [CrossRef]





| Grain Size (μm) | Annealing Temperature (°C) | |||
|---|---|---|---|---|
| 1000 | 1050 | 1100 | ||
| Annealing time (min) | 10 30 60 120 | 27.0 40.1 48.1 63.2 | 42.6 65.7 80.3 98.4 | 80.2 118.1 152.8 201.2 |
| Grain Size (μm) | Annealing Temperature (°C) | |||
|---|---|---|---|---|
| 900 | 950 | 1000 | ||
| Annealing time (min) | 120 300 600 1200 | 3.35 5.13 8.21 10.50 | 12.9 16.9 21.7 30.3 | 50.8 70.6 103.3 141.0 |
| Atomic Size Difference (%) | Grain Growth Activation Energy (kJ/mol) | ΔHmix (kJ/mol) | |
|---|---|---|---|
| Al0.3CoCrCu0.3FeNi | 3.65 | 761.3 | −4.38 |
| Al0.2CoCrFeMnNi | 2.77 | 434.4 | −6.24 |
| CoCrFeMnNi | 1.18 | 325.0 | −4.16 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.-S.; Tsai, P.-H.; Kuo, C.-M.; Tsai, C.-W. Effect of Atomic Size Difference on the Microstructure and Mechanical Properties of High-Entropy Alloys. Entropy 2018, 20, 967. https://doi.org/10.3390/e20120967
Wu C-S, Tsai P-H, Kuo C-M, Tsai C-W. Effect of Atomic Size Difference on the Microstructure and Mechanical Properties of High-Entropy Alloys. Entropy. 2018; 20(12):967. https://doi.org/10.3390/e20120967
Chicago/Turabian StyleWu, Chan-Sheng, Ping-Hsiu Tsai, Chia-Ming Kuo, and Che-Wei Tsai. 2018. "Effect of Atomic Size Difference on the Microstructure and Mechanical Properties of High-Entropy Alloys" Entropy 20, no. 12: 967. https://doi.org/10.3390/e20120967
APA StyleWu, C.-S., Tsai, P.-H., Kuo, C.-M., & Tsai, C.-W. (2018). Effect of Atomic Size Difference on the Microstructure and Mechanical Properties of High-Entropy Alloys. Entropy, 20(12), 967. https://doi.org/10.3390/e20120967






