A Joint Fault Diagnosis Scheme Based on Tensor Nuclear Norm Canonical Polyadic Decomposition and Multi-Scale Permutation Entropy for Gears
Abstract
:1. Introduction
1.1. Notation
1.2. Organization
2. Tensor Nuclear Norm Canonical Polyadic Decomposition (TNNCPD)
2.1. Tensor Canonical Polyadic Decomposition
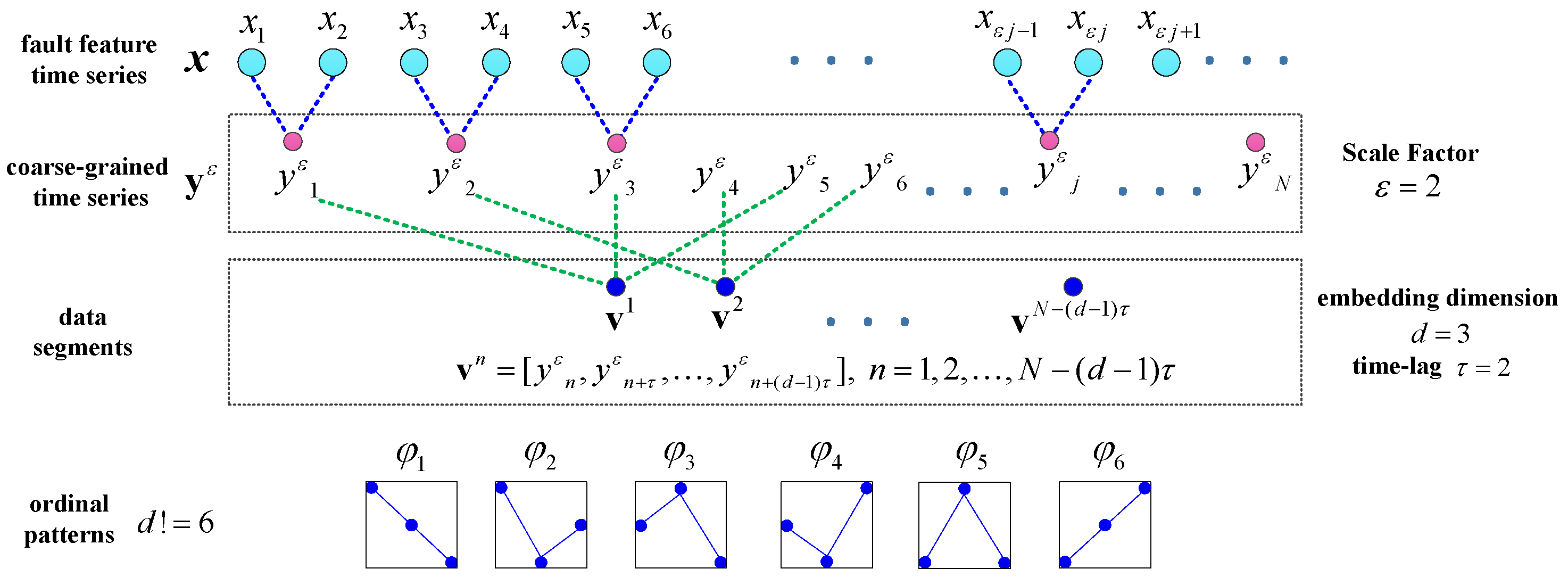
2.1.1. The Tensorization of One-Dimensional Vibration Signal Data
2.1.2. Tensor Canonical Polyadic Decomposition Based on the Least-Squares Algorithm (CPD-ALS)
2.2. Tensor Nuclear Norm Canonical Polyadic Decomposition (TNNCPD)
2.2.1. Matrix Nuclear Norm
2.2.2. Tensor Canonical Polyadic Decomposition Method Based on Nuclear Norm and Convex Optimization
2.2.3. The Working Algorithm
| Algorithm 1: TNNCPD |
| Input: Output: 1: Initialize: R order vectors in front of the of ; The largest number of iterations: ; convergence threshold: ; 2: while no convergence do 3: for to 3 do 4: 5: end for to 3 do 6: 7: end for 8: end |
2.2.4. Simulation Analysis
3. A Joint Fault Diagnosis Scheme Based on TNNCPD and MSPE
- (1)
- Vibration signals reflecting the different working conditions of gears are acquired through the vibration acceleration sensor.
- (2)
- The vibration signals are decomposed by the TNNCPD method to obtain the useful feature component.
- (3)
- The MSPE of the feature component is calculated as a fault feature vector. The calculation process of MSPE is as follows:
- (4)
- Enter the fault feature vector as the input of the BP neural network chosen fault classifier in order to achieve fault classification. The flowchart of the proposed method is depicted in Figure 9.
4. Experimental Signal Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yang, D.; Liu, Y.; Li, S.; Li, X.; Ma, L. Gear fault diagnosis based on support vector machine optimized by artificial bee colony algorithm. Mech. Mach. Theory 2015, 90, 219–229. [Google Scholar] [CrossRef]
- Forrester, B.D. Advanced Vibration Analysis Techniques for Fault Detection and Diagnosis in Geared Transmission Systems. PhD Thesis, Swinburne University of Technology, Hawthorn, Australia, 1996. [Google Scholar]
- Tan, C.K.; Irving, P.; Mba, D. A comparative experimental study on the diagnostic and prognostic capabilities of acoustics emission, vibration and spectrometric oil analysis for spur gears. Mech. Syst. Signal Process. 2007, 21, 208–233. [Google Scholar] [CrossRef] [Green Version]
- Heydarzadeh, M.; Nourani, M.; Hansen, J.; Kia, S.H. Non-invasive gearbox fault diagnosis using scattering transform of acoustic emission. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 371–375. [Google Scholar]
- Dalpiaz, G.; Rivola, A.; Rubini, R. Effectiveness and sensitivity of vibration processing techniques for local fault detection in gears. Mech. Syst. Signal Process. 2000, 14, 387–412. [Google Scholar] [CrossRef]
- Feng, Z.; Liang, M.; Zhang, Y.; Hou, S. Fault diagnosis for wind turbine planetary gearboxes via demodulation analysis based on ensemble empirical mode decomposition and energy separation. Renew. Energy 2012, 47, 112–126. [Google Scholar] [CrossRef]
- Wu, X.L.; Peter, W.T.; Gui, C.Z.; Tielin, S. Classification of gear faults using cumulants and the radial basis function network. Mech. Syst. Signal Process. 2004, 18, 381–389. [Google Scholar]
- Yi, C.; Lv, Y.; Xiao, H.; Huang, T.; You, G. Multisensor signal denoising based on matching synchrosqueezing wavelet transform for mechanical fault condition assessment. Meas. Sci. Technol. 2018. [Google Scholar] [CrossRef]
- Cheng, J.S.; Yu, Y.; Yu, D. The envelope order spectrum based on generalized demodulation time—Frequency analysis and its application to gear fault diagnosis. Mech. Syst. Signal Process. 2010, 24, 508–521. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, K.; Yang, Y. An order tracking technique for the gear fault diagnosis using local mean decomposition method. Mech. Mach. Theory 2012, 55, 67–76. [Google Scholar] [CrossRef]
- Saravanan, N.; Ramachandran, K.I. Incipient gear box fault diagnosis using discrete wavelet transform (DWT) for feature extraction and classification using artificial neural network (ANN). Expert Syst. Appl. 2010, 37, 4168–4181. [Google Scholar] [CrossRef]
- Kennel, M.B.; Brown, R.; Abarbanel, H.D.I. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403. [Google Scholar] [CrossRef] [PubMed]
- Su, Z.; Zhang, Y.; Jia, M.; Xu, F.; Hu, J. Gear fault identification and classification of singular value decomposition based on Hilbert-Huang transform. J. Mech. Sci. Technol. 2011, 25, 267–272. [Google Scholar] [CrossRef]
- Kouchaki, S.; Sanei, S.; Arbon, E.L.; Dijk, D.J. Tensor based singular spectrum analysis for automatic scoring of sleep EEG. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 23, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Yi, C.; Lv, Y.; Ge, M.; Xiao, H.; Yu, X. Tensor Singular Spectrum Decomposition Algorithm Based on Permutation Entropy for Rolling Bearing Fault Diagnosis. Entropy 2017, 19, 139. [Google Scholar] [CrossRef]
- Cichocki, A.; Mandic, D.; de Lathauwer, L.; de Lathauwer, L.; Zhou, G.; Zhao, Q.; Caiafa, C.; Phan, H.A. Tensor decompositions for signal processing applications: From two-way to multiway component analysis. IEEE Signal Process. Mag. 2015, 32, 145–163. [Google Scholar] [CrossRef]
- Domanov, I.; de Lathauwer, L. Canonical polyadic decomposition of third-order tensors: Reduction to generalized eigenvalue decomposition. SIAM J. Matrix Anal. Appl. 2014, 35, 636–660. [Google Scholar] [CrossRef]
- Sidiropoulos, N.D.; de Lathauwer, L.; Fu, X.; Huang, K.; Papalexakis, E.E.; Faloutsos, C. Tensor decomposition for signal processing and machine learning. IEEE Trans. Signal Process. 2017, 65, 3551–3582. [Google Scholar] [CrossRef]
- Phan, A.H.; Cichocki, A. Tensor decompositions for feature extraction and classification of high dimensional datasets. Nonlinear Theory Its Appl. IEICE 2010, 1, 37–68. [Google Scholar] [CrossRef]
- Recht, B.; Fazel, M.; Parrilo, P.A. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. SIAM Rev. 2010, 52, 471–501. [Google Scholar] [CrossRef]
- Candès, E.J.; Recht, B. Exact matrix completion via convex optimization. Found. Comput. Math. 2009, 9, 717. [Google Scholar] [CrossRef]
- Yi, C.; Lv, Y.; Xiao, H.; Ke, K.; Yu, X. A novel baseline correction method using convex optimization framework in laser-induced breakdown spectroscopy quantitative analysis. Spectrochim. Acta Part B At. Spectrosc. 2017, 138, 72–80. [Google Scholar] [CrossRef]
- De, S.C.; Olukotun, K.; Ré, C. Global convergence of stochastic gradient descent for some non-convex matrix problems. arXiv, 2014; arXiv:1411.1134. [Google Scholar]
- Gu, S.; Zhang, L.; Zuo, W.; Feng, X. Weighted nuclear norm minimization with application to image denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2862–2869. [Google Scholar]
- Debals, O.; van Barel, M.; de Lathauwer, L. Löwner-Based Blind Signal Separation of Rational Functions with Applications. IEEE Trans. Signal Process. 2016, 64, 1909–1918. [Google Scholar] [CrossRef]
- Donoho, D.; Gavish, M. Minimax risk of matrix denoising by singular value thresholding. Ann. Stat. 2014, 42, 2413–2440. [Google Scholar] [CrossRef]
- Zhang, L.; Xiong, G.; Liu, H.; Zou, H.; Guo, W. Bearing fault diagnosis using multi-scale entropy and adaptive neuro-fuzzy inference. Expert Syst. Appl. 2010, 37, 6077–6085. [Google Scholar] [CrossRef]
- Morabito, F.C.; Labate, D.; la Foresta, F.; Bramanti, A.; Morabito, G.; Palamara, I. Multivariate multi-scale permutation entropy for complexity analysis of Alzheimer’s disease EEG. Entropy 2012, 14, 1186–1202. [Google Scholar] [CrossRef]
- Zhao, L.Y.; Wang, L.; Yan, R.Q. Rolling bearing fault diagnosis based on wavelet packet decomposition and multi-scale permutation entropy. Entropy 2015, 17, 6447–6461. [Google Scholar] [CrossRef]
- Wang, S.; Liu, H.; Xu, X. Fan fault diagnosis based on symmetrized dot pattern and improved BP neural network. In Proceedings of the 2016 3rd International Conference on Materials Engineering, Manufacturing Technology and Control, Taiyuan, China, 27–28 February 2016. [Google Scholar]
- Erichson, N.B.; Voronin, S.; Brunton, S.L.; Kutz, J.N. Randomized matrix decompositions using R. arXiv, 2016; arXiv:1608.02148. [Google Scholar]
- Ma, S.; Goldfarb, D.; Chen, L. Fixed point and Bregman iterative methods for matrix rank minimization. Math. Program. 2011, 128, 321–353. [Google Scholar] [CrossRef]
- Ji, S.; Ye, J. An accelerated gradient method for trace norm minimization. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; pp. 457–464. [Google Scholar]
- McFadden, P.D. Examination of a technique for the early detection of failure in gears by signal processing of the time domain average of the meshing vibration. Mech. Syst. Signal Process. 1987, 1, 173–183. [Google Scholar] [CrossRef]
- Tanner, J.; Wei, K. Normalized iterative hard thresholding for matrix completion. SIAM J. Sci. Comput. 2013, 35, S104–S125. [Google Scholar] [CrossRef]























| SSA | WT | CPD-ALS | The Proposed Method | |
|---|---|---|---|---|
| correlation coefficient | 0.8142 | 0.8352 | 0.7051 | 0.9351 |
| Operating State | Set | MSPE | Combining WT with MSPE | Proposed Scheme |
|---|---|---|---|---|
| no load | train | 80% | 90% | 100% |
| test | 66.07% | 76.79% | 100% | |
| a load of 10 N/m | train | 75% | 90% | 100% |
| test | 53.57% | 80.36% | 100% | |
| a load of 20 N/m | train | 40% | 70% | 100% |
| test | 23.21% | 64.28% | 98.21% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, M.; Lv, Y.; Yi, C.; Zhang, Y.; Chen, X. A Joint Fault Diagnosis Scheme Based on Tensor Nuclear Norm Canonical Polyadic Decomposition and Multi-Scale Permutation Entropy for Gears. Entropy 2018, 20, 161. https://doi.org/10.3390/e20030161
Ge M, Lv Y, Yi C, Zhang Y, Chen X. A Joint Fault Diagnosis Scheme Based on Tensor Nuclear Norm Canonical Polyadic Decomposition and Multi-Scale Permutation Entropy for Gears. Entropy. 2018; 20(3):161. https://doi.org/10.3390/e20030161
Chicago/Turabian StyleGe, Mao, Yong Lv, Cancan Yi, Yi Zhang, and Xiangjun Chen. 2018. "A Joint Fault Diagnosis Scheme Based on Tensor Nuclear Norm Canonical Polyadic Decomposition and Multi-Scale Permutation Entropy for Gears" Entropy 20, no. 3: 161. https://doi.org/10.3390/e20030161
APA StyleGe, M., Lv, Y., Yi, C., Zhang, Y., & Chen, X. (2018). A Joint Fault Diagnosis Scheme Based on Tensor Nuclear Norm Canonical Polyadic Decomposition and Multi-Scale Permutation Entropy for Gears. Entropy, 20(3), 161. https://doi.org/10.3390/e20030161






