Abstract
In this paper, we give upper bounds for the rate-distortion function (RDF) of any Gaussian vector, and we propose coding strategies to achieve such bounds. We use these strategies to reduce the computational complexity of coding Gaussian asymptotically wide sense stationary (AWSS) autoregressive (AR) sources. Furthermore, we also give sufficient conditions for AR processes to be AWSS.
1. Introduction
In 1956, Kolmogorov [1] gave a formula for the rate-distortion function (RDF) of Gaussian vectors and the RDF of Gaussian wide sense stationary (WSS) sources. Later, in 1970 Gray [2] obtained a formula for the RDF of Gaussian autoregressive (AR) sources.
In 1973, Pearl [3] gave an upper bound for the RDF of finite-length data blocks of Gaussian WSS sources, but he did not propose a coding strategy to achieve his bound for a given block length. In [4], we presented two tighter upper bounds for the RDF of finite-length data blocks of Gaussian WSS sources, and we proposed low-complexity coding strategies, based on the discrete Fourier transform (DFT), to achieve such bounds. Moreover, we proved that those two upper bounds tend to the RDF of the WSS source (computed by Kolmogorov in [1]) when the size of the data block grows.
In the present paper, we generalize the upper bounds and the two low-complexity coding strategies presented in [4] to any Gaussian vector. Therefore, in contrast to [4], here no assumption about the structure of the correlation matrix of the Gaussian vector has been made (observe that since the sources in [4] were WSS the correlation matrix of the Gaussian vectors there considered was Toeplitz). To obtain such generalization we start our analysis by first proving several new results on the DFT of random vectors. Although in [4] (Theorem 1) another new result on the DFT was presented, it cannot be used here, because such result and its proof rely on the power spectral density (PSD) of a WSS process and its properties.
The two low-complexity strategies here presented are applied in coding finite-length data blocks of Gaussian AR sources. Specifically, we prove that the rates (upper bounds) corresponding to these two strategies tend to the RDF of the AR source (computed by Gray in [2]) when the size of the data block grows and the AR source is asymptotically WSS (AWSS).
The definition of AWSS process was introduced by Gray in [5] (Chapter 6) and it is based on his concept of asymptotically equivalent sequences of matrices [6]. Sufficient conditions for AR processes to be AWSS can be found in [5] (Theorem 6.2) and [7] (Theorem 7). In this paper we present other sufficient conditions which make easier to check in practice whether an AR process is AWSS.
The paper is organized as follows. In Section 2 we obtain several new results on the DFT of random vectors which are used in Section 3. In Section 3 we give upper bounds for the RDF of Gaussian vectors, and we propose coding strategies to achieve such bounds. In Section 4 we apply the strategies proposed in Section 3 to reduce the computational complexity of coding Gaussian AWSS AR sources. In Section 5 we give sufficient conditions for AR processes to be AWSS. We finish the paper with a numerical example and conclusions.
2. Several New Results on the DFT of Random Vectors
We begin by introducing some notation. denotes the set of (finite) complex numbers, is the imaginary unit, and denote real and imaginary parts, respectively. * stands for conjugate transpose, ⊤ denotes transpose, and , , are the eigenvalues of an Hermitian matrix A arranged in decreasing order. E stands for expectation, and is the Fourier unitary matrix, i.e.,
If then denotes the real (column) vector
If for all then is the n-dimensional vector given by
In this section, we give several new results on the DFT of random vectors in two theorems and one lemma.
Theorem 1.
Let be the DFT of an n-dimensional random vector , that is, .
- If thenand
- If the random vector is real and thenand
Proof.
(1) We first prove that if is an unitary matrix then
We have
for all , and hence,
Let be a diagonalization of where the eigenvector matrix is unitary. As
Analogously, it can be proved that
To finish the proof we only need to show that
If are n real numbers then
and thus,
Lemma 1.
Let be the DFT of an n-dimensional random vector . If then
- .
- .
- .
- .
- .
Proof.
(1) It is a direct consequence of Equation (7).
(2) We have
(3) Observe that
and hence,
(4) and (5) From Equation (10) we obtain
Furthermore,
Theorem 2.
Let be the DFT of a real n-dimensional random vector . If then
Proof.
Fix and consider a real unit eigenvector corresponding to . We have
From [4] (Equation (10)) we obtain
with
and consequently,
with being a diagonalization of where the eigenvector matrix is unitary. Therefore,
To finish the proof we only need to show that
3. RDF Upper Bounds for Real Gaussian Vectors
We first review the formula for the RDF of a real Gaussian vector given by Kolmogorov in [1].
Theorem 3.
If is a real zero-mean Gaussian n-dimensional vector with positive definite correlation matrix, its RDF is given by
where denotes trace and θ is a real number satisfying
We recall that can be thought of as the minimum rate (measured in nats) at which one must encode (compress) in order to be able to recover it with a mean square error (MSE) per dimension not larger than D, that is:
where denotes the estimation of and is the spectral norm.
The following result provides an optimal coding strategy for in order to achieve whenever . Observe that if then
Corollary 1.
Suppose that is as in Theorem 3. Let be a diagonalization of where the eigenvector matrix is real and orthogonal. If then
with .
Proof.
We encode separately with for all . Let , where
As is unitary (in fact, it is a real orthogonal matrix) and the spectral norm is unitarily invariant, we have
and thus,
Hence, applying Equation (13) yields
☐
Corollary 1 shows that an optimal coding strategy for is to encode separately.
We now give two coding strategies for based on the DFT whose computational complexity is lower than the computational complexity of the optimal coding strategy provided in Corollary 1.
Theorem 4.
Let be as in Theorem 3. Suppose that is the DFT of and . Then
where is the Frobenius norm,
and
Proof.
Equations (15) and (16) were presented in [4] (Equations (16) and (20)) for the case where the correlation matrix is Toeplitz. They were proved by using a result on the DFT of random vectors with Toeplitz correlation matrix, namely, ref. [4] (Theorem 1). The proof of Theorem 4 is similar to the proof of [4] (Equations (16) and (20)) but using Theorem 1 instead of [4] (Theorem 1). Observe that in Theorems 1 and 4 no assumption about the structure of has been made. ☐
Theorem 4 shows that a coding strategy for is to encode separately, where denotes the smallest integer higher than or equal to . Theorem 4 also shows that another coding strategy for is to encode separately the real part and the imaginary part of instead of encoding when . The computational complexity of these two coding strategies based on the DFT is lower than the computational complexity of the optimal coding strategy provided in Corollary 1. Specifically, the complexity of computing the DFT () is whenever the fast Fourier transform (FFT) algorithm is used, while the complexity of computing is . Moreover, when the coding strategies based on the DFT are used, we do not need to compute a real orthogonal eigenvector matrix of . It should also be mentioned that for these coding strategies based on the DFT the knowledge of is not even required, in fact, for them we only need to know with .
The rates corresponding to the two coding strategies given in Theorem 4, and , can be written in terms of and by using Lemma 1 and the following lemma.
Lemma 2.
Let and D be as in Theorem 4. Then
- for all .
- for all .
- for all .
- for all .
Proof.
Assertion (1) now follows directly from Equation (13).
(2) Applying Theorem 2 we have
Consequently, from Equation (13) we obtain
Assertions (3) and (4) Applying Equations (3) and (4) yields
and
Assertions (3) and (4) now follow directly from Equation (13). ☐
We end this section with a result that is a direct consequence of Lemma 2. This result shows when the rates corresponding to the two coding strategies given in Theorem 4, and , are equal.
Lemma 3.
Let , , and D be as in Theorem 4. Then the two following assertions are equivalent:
- .
- for all .
Proof.
Fix . From Lemma 2 we have
☐
4. Low-Complexity Coding Strategies for Gaussian AWSS AR Sources
We begin by introducing some notation. The symbols , , and denote the set of positive integers, integers, and (finite) real numbers, respectively. If is continuous and -periodic, we denote by the Toeplitz matrix given by
where is the sequence of Fourier coefficients of f, i.e.,
If and are matrices for all , we write if the sequences and are asymptotically equivalent, that is, and are bounded and (see [5] (Section 2.3) and [6]).
We now review the definitions of AWSS processes and AR processes.
Definition 1.
A random process is said to be AWSS if it has constant mean (i.e., for all and there exists a continuous -periodic function such that . The function f is called (asymptotic) PSD of .
Definition 2.
A real zero-mean random process is said to be AR if
or equivalently,
where , for all , and is a real zero-mean random process satisfying that for all with and being the Kronecker delta (i.e., if , and it is zero otherwise).
The AR process in Equation (17) is of finite order if there exists such that for all . In this case, is called an AR process.
The following theorem shows that if is a large enough data block of a Gaussian AWSS AR source, the rate does not increase whenever we encode it using the two coding strategies based on the DFT presented in Section 3, instead of encoding using an eigenvector matrix of its correlation matrix.
Theorem 5.
Let be as in Definition 2. Suppose that , with for all , is the sequence of Fourier coefficients of a function which is continuous and -periodic. Then
Proof. (1) Equation (17) can be rewritten as
Consequently,
As , is invertible, and therefore,
for all , where is a singular value decomposition of . Thus, applying [8] (Theorem 4.3) yields
(2a) From Equation (13) we have
Assertion (2a) now follows from Theorem 4 and Assertion (1).
(2b) From Assertion (2a) we only need to show that
As the Frobenius norm is unitarily invariant we obtain
where f is (asymptotic) PSD of and . Assertion (2b) now follows from and [9] (Lemma 4.2). ☐
If , there always exists such function a and it is given by for all (see, e.g., [8] (Appendix B)). In particular, if is an AR process, for all .
5. Sufficient Conditions for AR Processes to be AWSS
In the following two results we give sufficient conditions for AR processes to be AWSS.
Theorem 6.
Let be as in Definition 2. Suppose that , with for all , is the sequence of Fourier coefficients of a function which is continuous and -periodic. Then the following assertions are equivalent:
- is AWSS.
- is bounded.
- is stable (that is, is bounded).
- for all and is AWSS with (asymptotic) PSD .
Proof.
(1)⇒(2) This is a direct consequence of the definition of AWSS process, i.e., of Definition 1.
(2)⇔(3) From Equation (20) we have
for all .
(3)⇒(4) It is well known that if is continuous and -periodic, and is stable then for all . Hence, for all .
Applying [8] (Lemma 4.2.1) yields . Consequently, from [7] (Theorem 3) we obtain
Observe that the sequence
is bounded. As the function is real, applying [8] (Theorem 4.4) we have that is Hermitian and for all , and therefore,
Thus, from [5] (Theorem 1.4) we obtain
Hence, applying [10] (Theorem 4.2) and [5] (Theorem 1.2) yields
Consequently, from [8] (Lemma 3.1.3) and [8] (Lemma 4.2.3) we have
(4)⇒(1) It is obvious.
Corollary 2.
Let be as in Definition 2 with . If for all then is AWSS.
Proof.
It is well known that if a sequence of complex numbers satisfies that and that for all then is stable with for all . Therefore, is stable with for all . Thus,
is bounded with for all . As is stable, from Theorem 6 we conclude that is AWSS. ☐
6. Numerical Example and Conclusions
6.1. Example
Let be as in Definition 2 with for all . Observe that . If from Corollary 2 we obtain that the process is AWSS. Figure 1 shows , , and by assuming that is Gaussian, , , , and . Figure 1 also shows the highest upper bound of presented in Theorem 5, namely, . Observe that the figure bears evidence of the equalities and inequalities given in Equations (18) and (19).
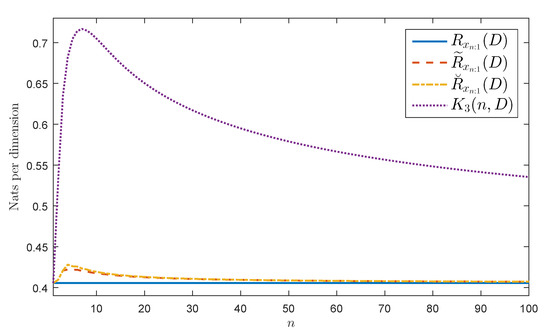
Figure 1.
Considered rates for a Gaussian AWSS AR(1) source.
6.2. Conclusions
The computational complexity of coding finite-length data blocks of Gaussian sources can be reduced by using any of the two low-complexity coding strategies here presented instead of the optimal coding strategy. Moreover, the rate does not increase if we use those strategies instead of the optimal one whenever the Gaussian source is AWSS and AR, and the considered data block is large enough.
Author Contributions
Authors are listed in order of their degree of involvement in the work, with the most active contributors listed first. All authors have read and approved the final manuscript.
Funding
This work was supported in part by the Spanish Ministry of Economy and Competitiveness through the CARMEN project (TEC2016-75067-C4-3-R).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kolmogorov, A.N. On the Shannon theory of information transmission in the case of continuous signals. IRE Trans. Inf. Theory 1956, 2, 102–108. [Google Scholar] [CrossRef]
- Gray, R.M. Information rates of autoregressive processes. IEEE Trans. Inf. Theory 1970, 16, 412–421. [Google Scholar] [CrossRef]
- Pearl, J. On coding and filtering stationary signals by discrete Fourier transforms. IEEE Trans. Inf. Theory 1973, 19, 229–232. [Google Scholar] [CrossRef]
- Gutiérrez-Gutiérrez, J.; Zárraga-Rodríguez, M.; Insausti, X. Upper bounds for the rate distortion function of finite-length data blocks of Gaussian WSS sources. Entropy 2017, 19, 554. [Google Scholar] [CrossRef]
- Gray, R.M. Toeplitz and circulant matrices: A review. Found. Trends Commun. Inf. Theory 2006, 2, 155–239. [Google Scholar] [CrossRef]
- Gray, R.M. On the asymptotic eigenvalue distribution of Toeplitz matrices. IEEE Trans. Inf. Theory 1972, 18, 725–730. [Google Scholar] [CrossRef]
- Gutiérrez-Gutiérrez, J.; Crespo, P.M. Asymptotically equivalent sequences of matrices and multivariate ARMA processes. IEEE Trans. Inf. Theory 2011, 57, 5444–5454. [Google Scholar] [CrossRef]
- Gutiérrez-Gutiérrez, J.; Crespo, P.M. Block Toeplitz matrices: Asymptotic results and applications. Found. Trends Commun. Inf. Theory 2011, 8, 179–257. [Google Scholar] [CrossRef]
- Gutiérrez-Gutiérrez, J.; Zárraga-Rodríguez, M.; Insausti, X.; Hogstad, B.O. On the complexity reduction of coding WSS vector processes by using a sequence of block circulant matrices. Entropy 2017, 19, 95. [Google Scholar] [CrossRef]
- Gutiérrez-Gutiérrez, J.; Crespo, P.M. Asymptotically equivalent sequences of matrices and Hermitian block Toeplitz matrices with continuous symbols: Applications to MIMO systems. IEEE Trans. Inf. Theory 2008, 54, 5671–5680. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).