Strong Secrecy on a Class of Degraded Broadcast Channels Using Polar Codes
Abstract
:1. Introduction
1.1. Relation to Prior Work
- To provide strong secrecy. Despite both weak and strong secrecy conditions resulting in the same secrecy-capacity region, the weak secrecy requirement in practical applications can result in important system vulnerabilities [19] (Section 3.3).
- To provide polar coding schemes that are implementable in practice. Notice in [13] (Figure 1) that the coding scheme presented in [10] relies on a construction for which no efficient code is presently known. Moreover, the polar coding scheme in [12] relies on the existence, through averaging, of certain deterministic mappings for the encoding/decoding process.
1.2. Overview of Novel Contributions
- Scenario. This paper focuses on two different models of the DBC with an arbitrary number of legitimate receivers and an arbitrary number of eavesdroppers for which polar codes have not yet been proposed. These two models arise very commonly in wireless communications.
- Existence of the polar coding schemes. We prove the existence for sufficiently large n of two secrecy-capacity achieving polar coding schemes under the strong secrecy condition.
- Practical implementation. We provide polar codes that are implementable in real communication systems, and we discuss further how to construct them in practice. As far as we know, although the construction of polar codes has been covered in a large number of references (for instance, see [21,22,23]), they only focus on polar code constructions under reliability constraints.
- Performance evaluation. Simulations results are provided in order to evaluate the reliability and secrecy performance of the polar coding schemes. The performance is evaluated according to different design parameters of the practical code construction. As far as we know, this paper is the first to evaluate the secrecy performance in terms of the strong secrecy, which is done by upper-bounding the information leakage at the eavesdroppers.
1.3. Notation
1.4. Organization
2. System Model and Secrecy-Capacity Region
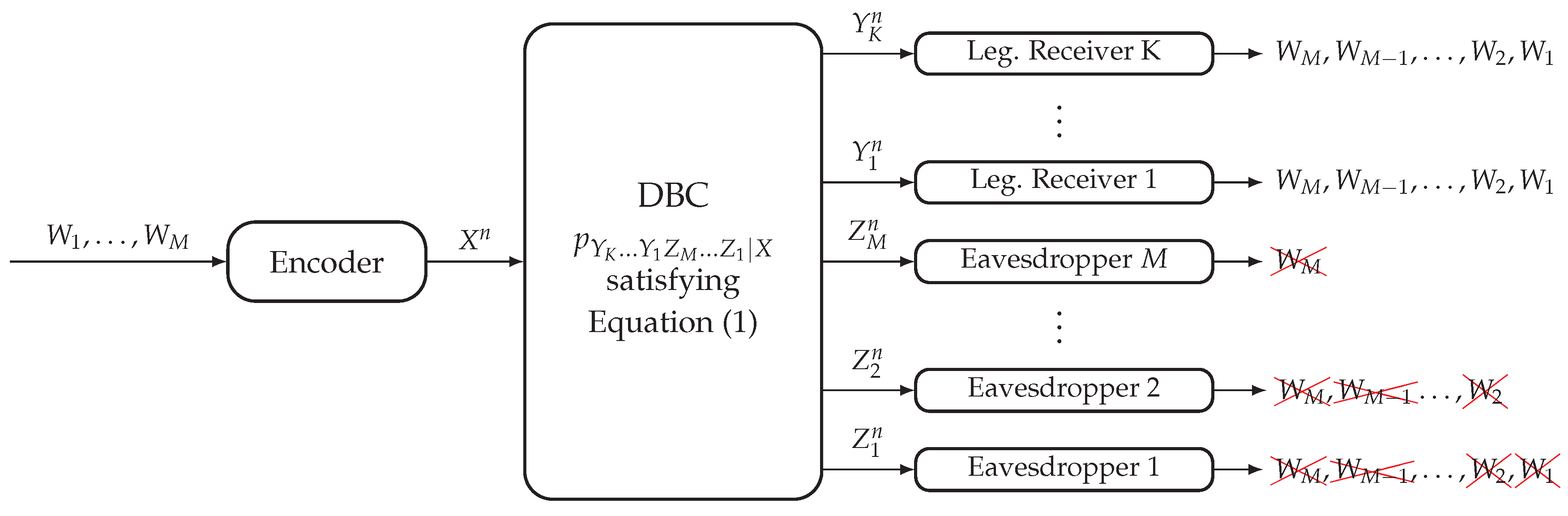
2.1. Degraded Broadcast Channel with Non-Layered Decoding and Layered Secrecy
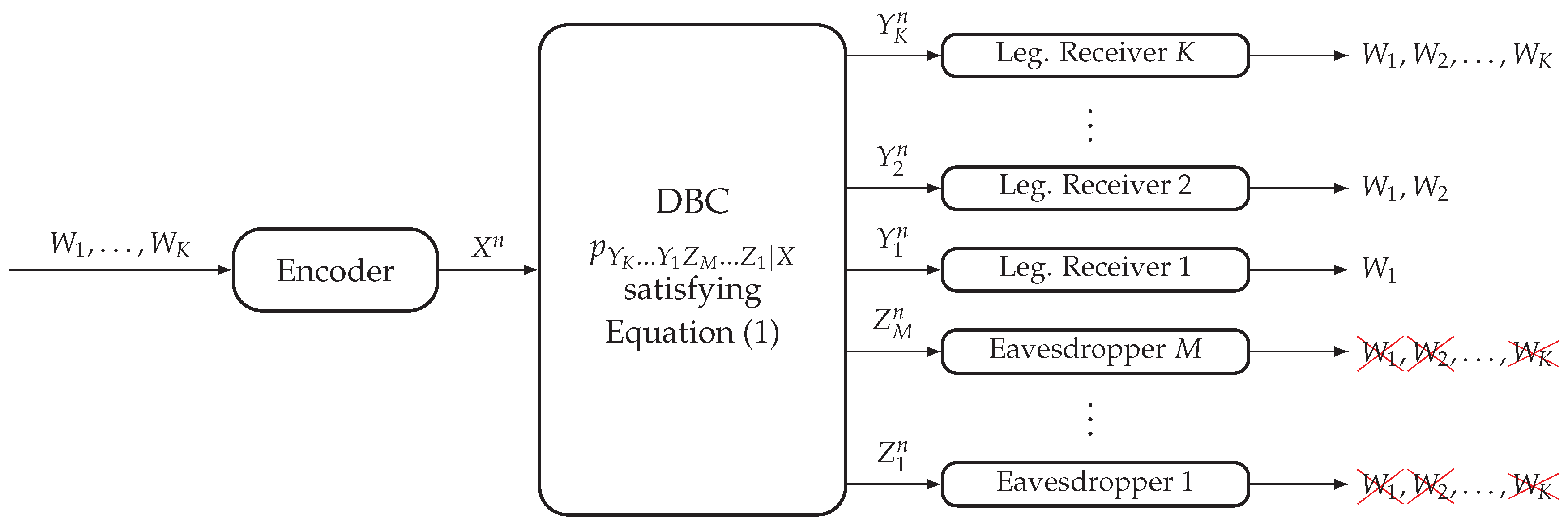
2.2. Degraded Broadcast Channel with Layered Decoding and Non-Layered Secrecy
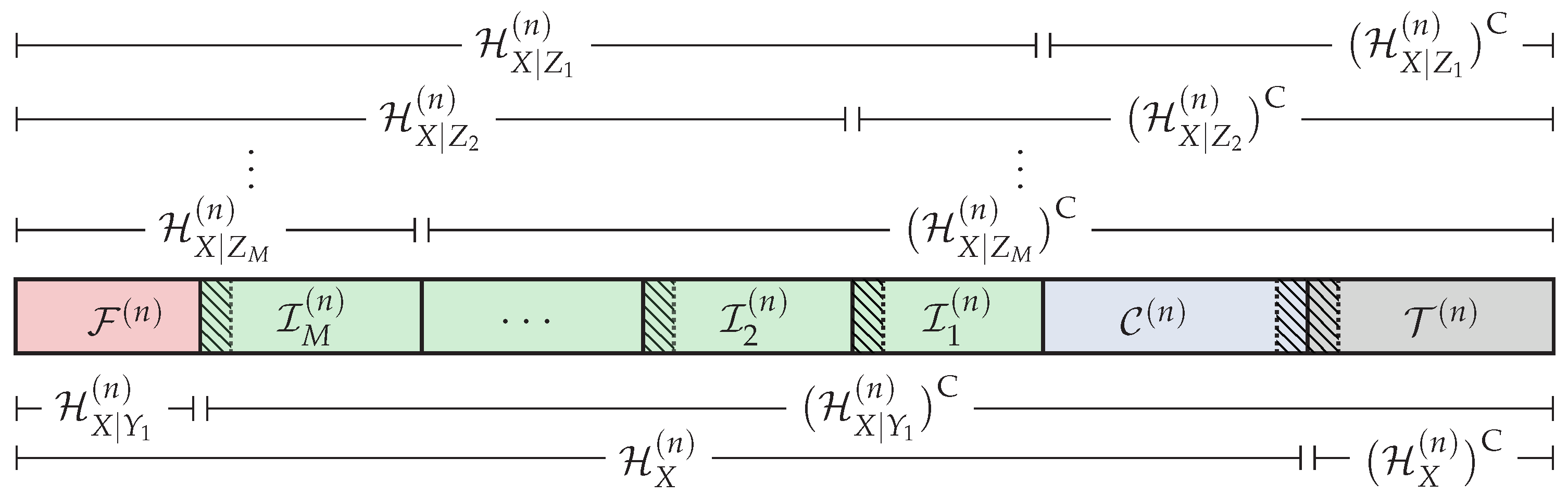
3. Review of Polar Codes
4. Polar Coding Scheme For the DBC-NLD-LS
4.1. Polar Code Construction
4.2. Polar Encoding
4.3. Polar Decoding
4.4. Information Leakage
4.5. Performance of the Polar Coding Scheme
4.5.1. Transmission Rates
4.5.2. Distribution of the DMS after the Polar Encoding
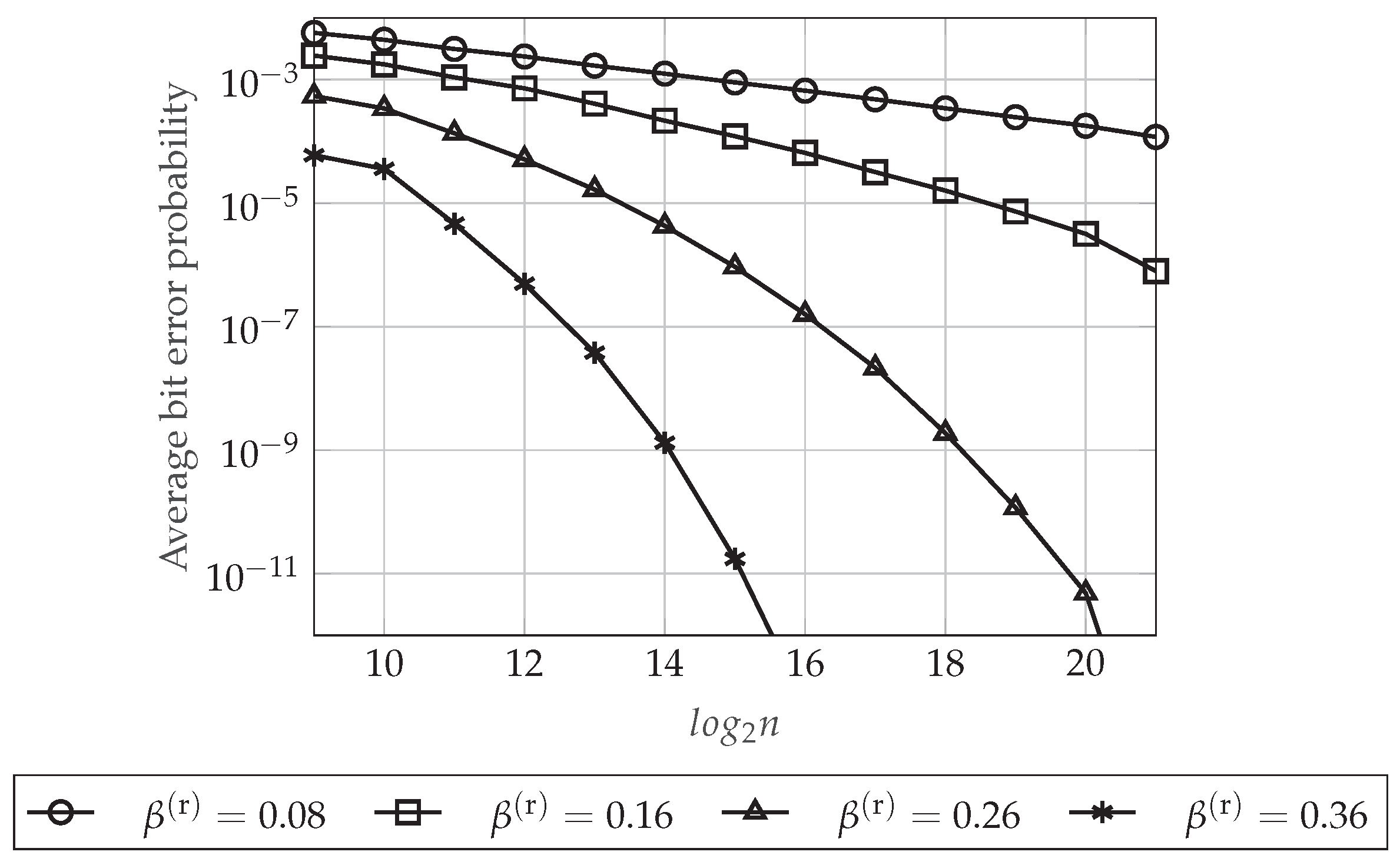
4.5.3. Reliability Performance
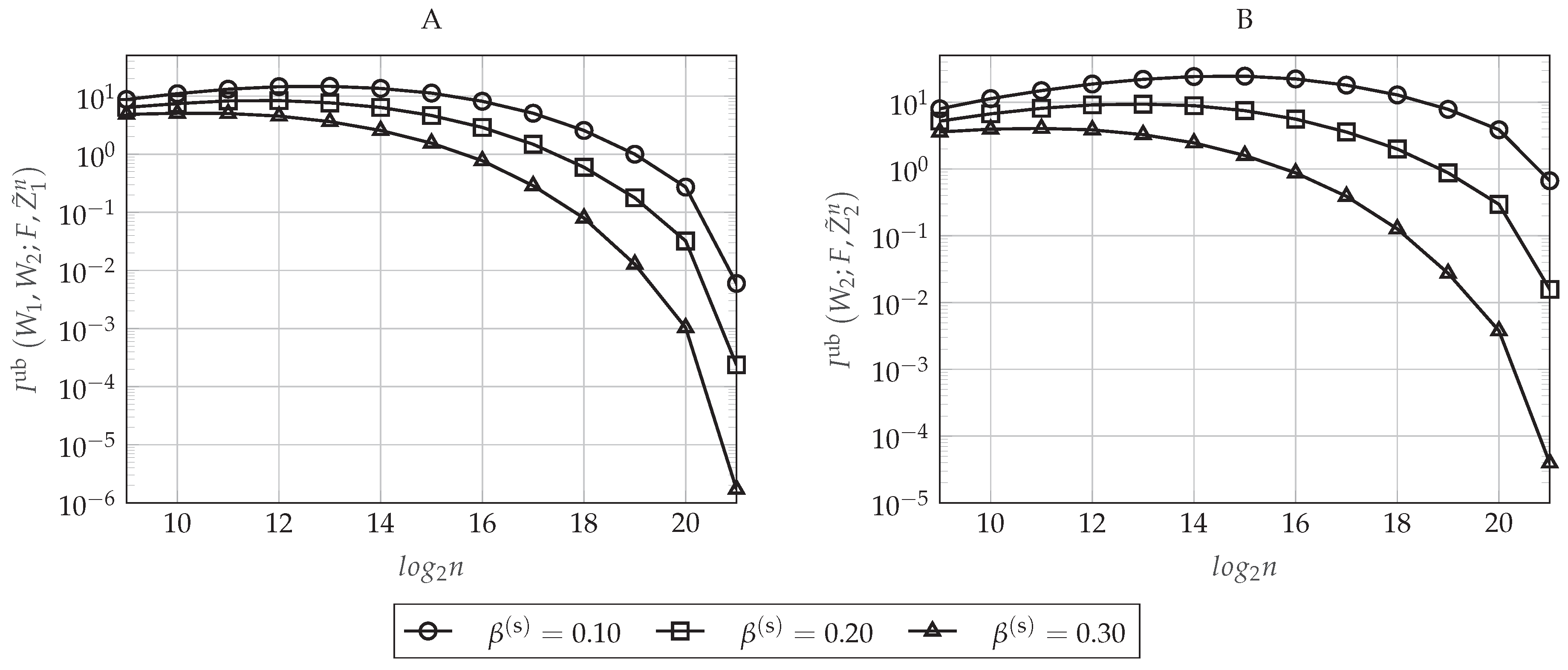
4.5.4. Secrecy Performance
4.5.5. Reuse of the Source of Common Randomness
5. Polar Coding Scheme for the DBC-LD-NLS
5.1. Polar Code Construction
5.2. Polar Encoding
5.3. Polar Decoding
5.4. Information Leakage
5.5. Performance of the Polar Coding Scheme
5.5.1. Transmission Rates
5.5.2. Distribution of the DMS after the Polar Encoding
5.5.3. Reliability Performance
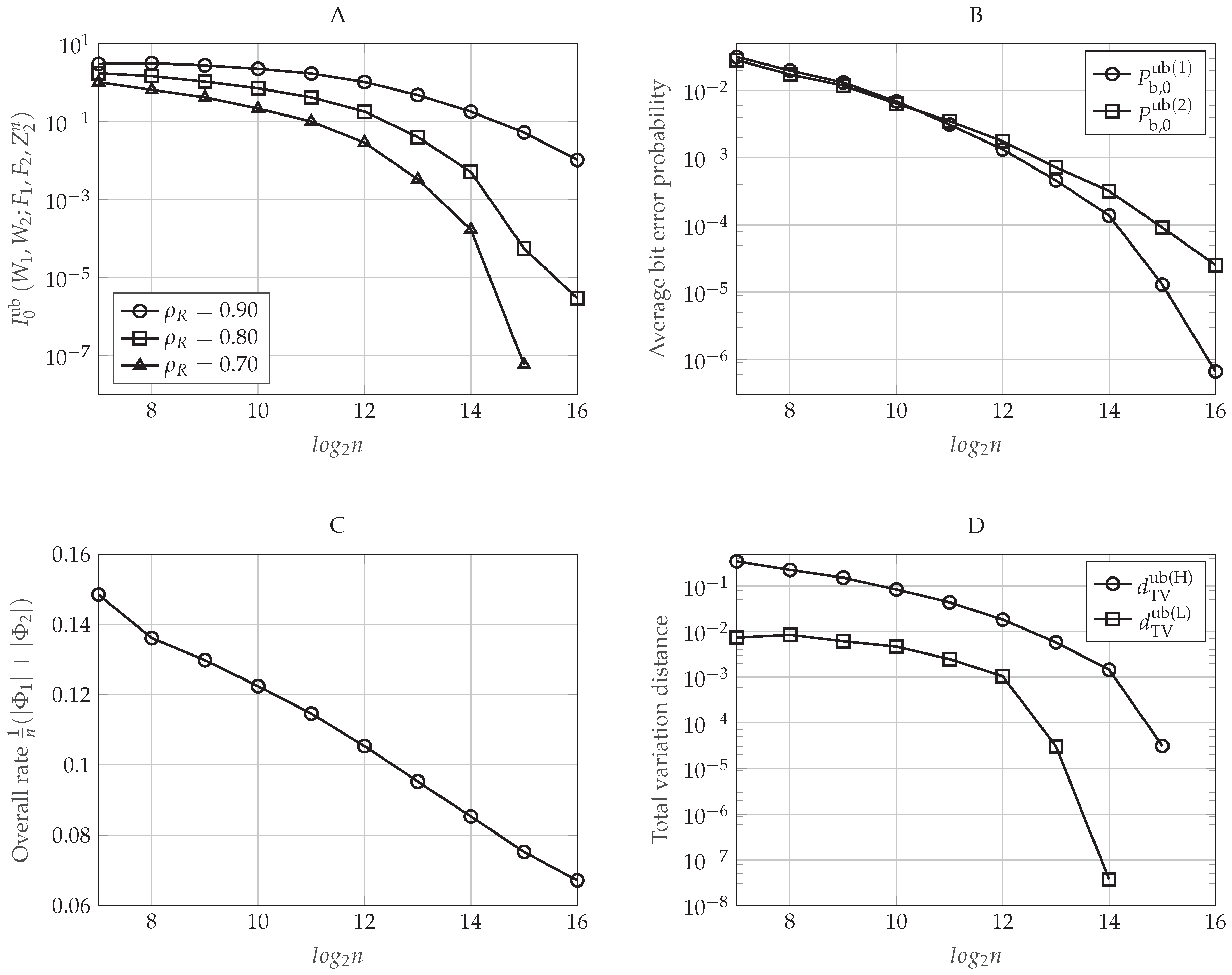
5.5.4. Secrecy Performance
6. Polar Construction and Performance Evaluation
6.1. DBC-NLD-LS
6.1.1. Practical Polar Code Construction
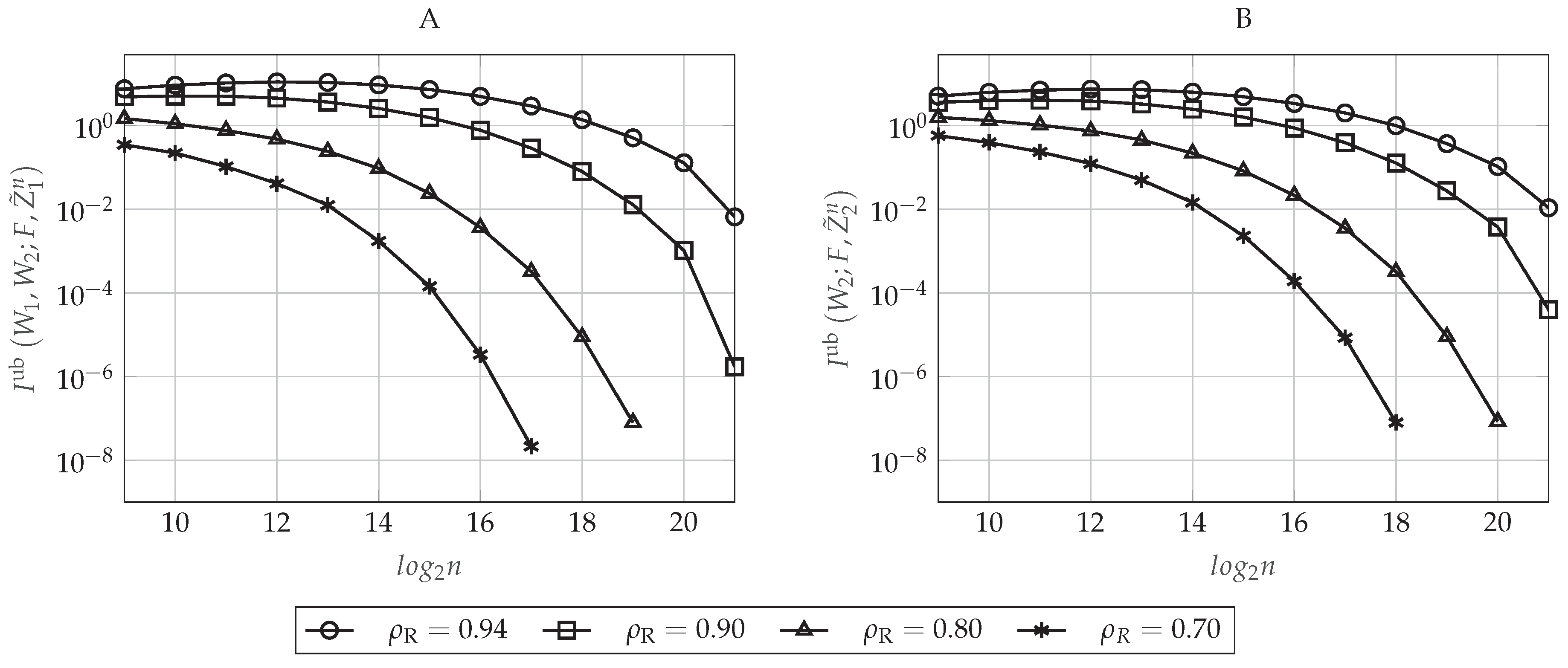
6.1.2. Performance Evaluation
6.2. DBC-LD-NLS
6.2.1. Practical Polar Code Construction
6.2.2. Performance Evaluation
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DBC | Degraded Broadcast Channel |
| DBC-NLD-LS | Degraded Broadcast Channel with Non-Layered Decoding and Layered Secrecy |
| DBC-LD-NLS | Degraded Broadcast Channel with Layered Decoding and Non-Layered Secrecy |
| SC | Successive Cancellation |
| DMS | Discrete Memoryless Source |
| BEC | Binary Erasure Channel |
| BSC | Binary Symmetric Channel |
| BE-BC | Binary Erasure Broadcast Channel |
| BS-BC | Binary Symmetric Broadcast Channel |
Appendix A. Proof of Lemmas 2 and 3
References and Notes
- Wyner, A. The wire-tap channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Csiszár, I.; Körner, J. Broadcast channels with confidential messages. IEEE Trans. Inf. Theory 1978, 24, 339–348. [Google Scholar] [CrossRef]
- Maurer, U.; Wolf, S. Information-theoretic key agreement: From weak to strong secrecy for free. In Advances in Cryptology—EUROCRYPT 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 351–368. [Google Scholar]
- Zou, S.; Liang, Y.; Lai, L.; Poor, H.; Shamai, S. Broadcast networks with layered decoding and layered secrecy: Theory and applications. Proc. IEEE 2015, 103, 1841–1856. [Google Scholar] [CrossRef]
- Liang, Y.; Lai, L.; Poor, H.V.; Shamai, S. A broadcast approach for fading wiretap channels. IEEE Trans. Inf. Theory 2014, 60, 842–858. [Google Scholar] [CrossRef]
- Ekrem, E.; Ulukus, S. Secrecy capacity of a class of broadcast channels with an eavesdropper. EURASIP J. Wirel. Commun. Netw. 2009, 2009. [Google Scholar] [CrossRef]
- Arikan, E. Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels. IEEE Trans. Inf. Theory 2009, 55, 3051–3073. [Google Scholar] [CrossRef] [Green Version]
- Mahdavifar, H.; Vardy, A. Achieving the secrecy capacity of wiretap channels using polar codes. IEEE Trans. Inf. Theory 2011, 57, 6428–6443. [Google Scholar] [CrossRef]
- Şaşoğlu, E.; Vardy, A. A new polar coding scheme for strong security on wiretap channels. In Proceedings of the IEEE International Symposium on Information Theory Proceedings (ISIT), Istanbul, Turkey, 7–12 July 2013; pp. 1117–1121. [Google Scholar] [CrossRef]
- Renes, J.M.; Renner, R.; Sutter, D. Efficient one-way secret key agreement and private channel coding via polarization. In Advances in Cryptology-ASIACRYPT; Springer: Berlin/Heidelberg, Germany, 2013; pp. 194–213. [Google Scholar]
- Wei, Y.; Ulukus, S. Polar coding for the general wiretap channel with extensions to multiuser scenarios. IEEE J. Sel. Areas Commun. 2016, 34, 278–291. [Google Scholar] [CrossRef]
- Cihad Gulcu, T.; Barg, A. Achieving secrecy capacity of the wiretap channel and broadcast channel with a confidential component. arXiv, 2014; arXiv:1410.3422. [Google Scholar]
- Chou, R.A.; Bloch, M.R. Polar coding for the broadcast channel with confidential messages: A random binning analogy. IEEE Trans. Inf. Theory 2016, 62, 2410–2429. [Google Scholar] [CrossRef]
- Goela, N.; Abbe, E.; Gastpar, M. Polar codes for broadcast channels. IEEE Trans. Inf. Theory 2015, 61, 758–782. [Google Scholar] [CrossRef]
- Chou, R.A.; Bloch, M.R.; Abbe, E. Polar coding for secret-key generation. IEEE Trans. Inf. Theory 2015, 61, 6213–6237. [Google Scholar] [CrossRef]
- Wang, L.; Sasoglu, E. Polar coding for interference networks. In Proceedings of the 2014 IEEE International Symposium on Information Theory, Honolulu, HI, USA, 29 June–4 July 2014; pp. 311–315. [Google Scholar] [CrossRef]
- Chou, R.A.; Yener, A. Polar coding for the multiple access wiretap channel via rate-splitting and cooperative jamming. In Proceedings of the 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 10–15 July 2016; pp. 983–987. [Google Scholar] [CrossRef]
- Hirche, C.; Morgan, C.; Wilde, M.M. Polar codes in network quantum information theory. IEEE Trans. Inf. Theory 2016, 62, 915–924. [Google Scholar] [CrossRef]
- Bloch, M.; Barros, J. Physical-Layer Security: From Information Theory to Security Engineering; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Chou, R.A.; Bloch, M.R. Using deterministic decisions for low-entropy bits in the encoding and decoding of polar codes. In Proceedings of the 2015 53rd Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 29 September–2 October 2015; pp. 1380–1385. [Google Scholar] [CrossRef]
- Tal, I.; Vardy, A. How to construct polar codes. IEEE Trans. Inf. Theory 2013, 59, 6562–6582. [Google Scholar] [CrossRef]
- Vangala, H.; Viterbo, E.; Hong, Y. A comparative study of polar code constructions for the AWGN channel. arXiv, 2015; arXiv:1501.02473. [Google Scholar]
- Honda, J.; Yamamoto, H. Polar coding without alphabet extension for asymmetric models. IEEE Trans. Inf. Theory 2013, 59, 7829–7838. [Google Scholar] [CrossRef]
- Throughout this paper, we assume binary polarization. An extension to q-ary alphabets is possible [25,26].
- Karzand, M.; Telatar, E. Polar codes for q-ary source coding. In Proceedings of the 2010 IEEE International Symposium on Information Theory, Austin, TX, USA, 12–18 June 2010; pp. 909–912. [Google Scholar] [CrossRef]
- Şasoğlu, E.; Telatar, E.; Arikan, E. Polarization for arbitrary discrete memoryless channels. In Proceedings of the IEEE Information Theory Workshop, Sicily, Italy, 11–16 October 2009; pp. 144–148. [Google Scholar]
- Arikan, E. Source polarization. In Proceedings of the 2010 IEEE International Symposium on Information Theory, Austin, TX, USA, 12–18 June 2010; pp. 899–903. [Google Scholar]
- Korada, S.B.; Urbanke, R.L. Polar codes are optimal for lossy source coding. IEEE Trans. Inf. Theory 2010, 56, 1751–1768. [Google Scholar] [CrossRef]
- Levin, D.A.; Peres, Y.; Wilmer, E.L. Markov Chains and Mixing Times; American Mathematical Society: Providence, RI, USA, 2009. [Google Scholar]
- Csiszar, I.; Körner, J. Information Theory: Coding Theorems for Discrete Memoryless Systems; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Pearl, J. Causality; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Most of the code in MATLAB is adapted from https://ecse.monash.edu/staff/eviterbo/polarcodes.html.
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Del Olmo Alos, J.; Rodríguez Fonollosa, J. Strong Secrecy on a Class of Degraded Broadcast Channels Using Polar Codes. Entropy 2018, 20, 467. https://doi.org/10.3390/e20060467
Del Olmo Alos J, Rodríguez Fonollosa J. Strong Secrecy on a Class of Degraded Broadcast Channels Using Polar Codes. Entropy. 2018; 20(6):467. https://doi.org/10.3390/e20060467
Chicago/Turabian StyleDel Olmo Alos, Jaume, and Javier Rodríguez Fonollosa. 2018. "Strong Secrecy on a Class of Degraded Broadcast Channels Using Polar Codes" Entropy 20, no. 6: 467. https://doi.org/10.3390/e20060467
APA StyleDel Olmo Alos, J., & Rodríguez Fonollosa, J. (2018). Strong Secrecy on a Class of Degraded Broadcast Channels Using Polar Codes. Entropy, 20(6), 467. https://doi.org/10.3390/e20060467





