Machine Learning Predictors of Extreme Events Occurring in Complex Dynamical Systems
Abstract
:1. Introduction
2. A Critical Overview of Binary Classification Methods
- True Positive (TP): an event predicted to be extreme that is actually extreme ;
- True Negative (TN): an event predicted to be quiescent that is actually quiescent ;
- False Positive (FP): an event predicted to be extreme that is actually quiescent ;
- False Negative (FN): an event predicted to be quiescent that is actually extreme .
2.1. Total and Balanced Error Rate
- First, total error rate is unsuited for unbalanced data. Extreme events are usually associated with extremely unbalanced datasets. This manifests in two ways. First, even a naive predictor may achieve very high accuracy, simply because always predicting “not extreme” is usually correct. Second, resampling the data (for instance, to balance the number of extreme and not-extreme training points) may widely change the total error rate, which in turn may change the optimal predictor.
- Second, this error metric is unsuited for strength-of-confidence measurement. It has no ability to distinguish between confidently classified points and and un-confidently classified points. This is particularly important if we expect our predictor to make many mistakes.
2.2. Score
2.3. Area under the Precision–Recall Curve
2.4. Volume under the Precision–Recall–Rate Surface
3. Separation of Extreme and Quiescent Events
- 1.
- , for all
- 2.
- and and
- 3.
- and
4. A Predictor Selection Criterion Adjusted for Extreme Events
4.1. Coinflip Indicator—Predictor
4.2. Bimodal Indicator—Predictor
4.3. Gaussian Indicator—Predictor
5. Applications
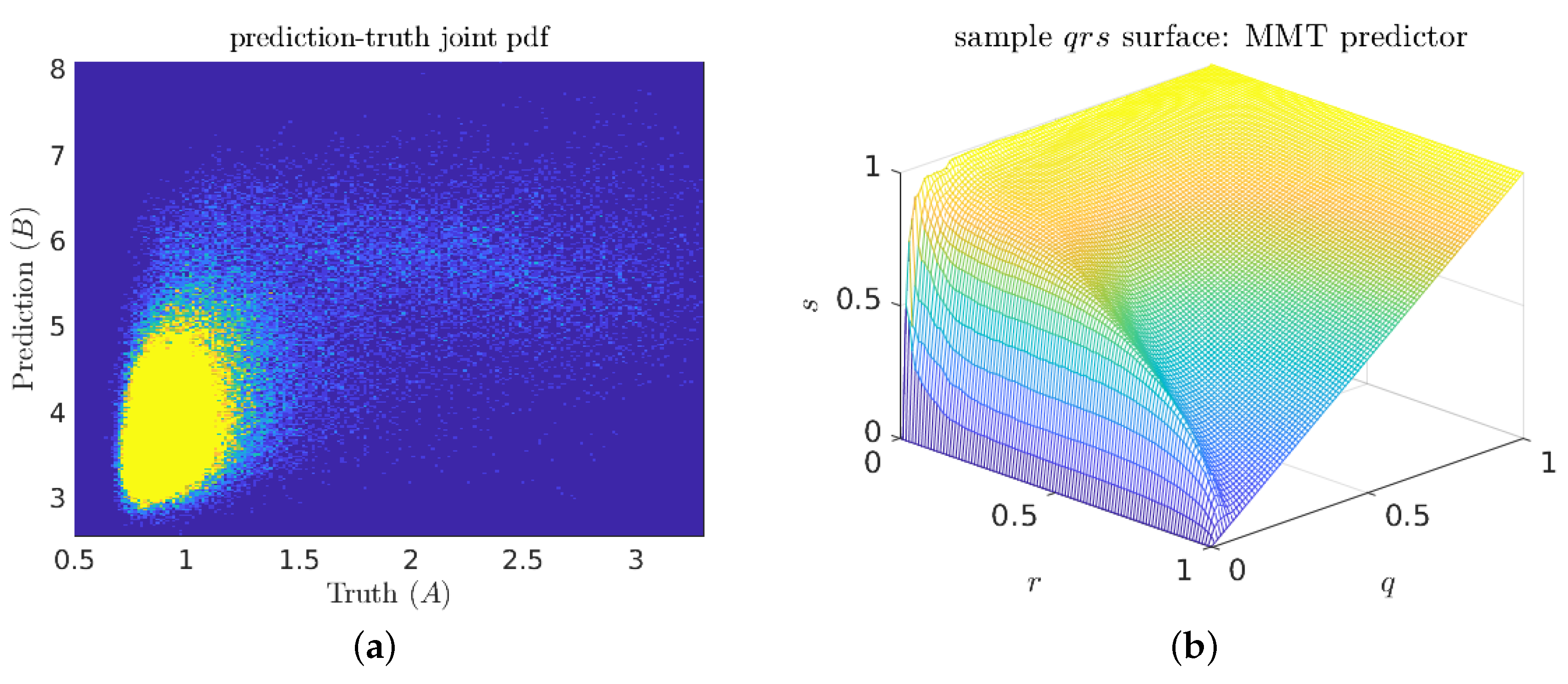
5.1. The Majda–McLaughlin–Tabak (MMT) Model
Numerical Results
5.2. The Kolmogorov Flow Model
Numerical Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chaloner, K.; Verdinelli, I. Bayesian Experimental Design: A Review. Stat. Sci. 1995, 10, 273–304. [Google Scholar] [CrossRef]
- Higham, D.J. An Algorithmic Introduction to Numerical Simulation of Stochastic Differential Equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
- Dysthe, K.; Krogstad, H.E.; Müller, P.; Muller, P. Oceanic Rogue Waves. Annu. Rev. Fluid Mech. 2008, 40, 287. [Google Scholar] [CrossRef]
- Kharif, C.; Pelinovsky, E.; Slunyaev, A. Rogue Waves in the Ocean, Observation, Theories and Modeling. In Advances in Geophysical and Environmental Mechanics and Mathematics Series; Springer: Berlin, Germany, 2009; Volume 14. [Google Scholar]
- Li, F. Modelling the Stock Market Using a Multi-Scale Approach. Master’s Thesis, University of Leicester, Leicester, UK, 2017. [Google Scholar]
- Kashiwagi, A.; Urabe, I.; Kaneko, K.; Yomo, T. Adaptive Response of a Gene Network to Environmental Changes by Fitness-Induced Attractor Selection. PLoS ONE 2006, 1, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Zio, E.; Pedroni, N. Estimation of the functional failure probability of a thermal-hydraulic passive system by Subset Simulation. Nucl. Eng. Des. 2009, 239, 580–599. [Google Scholar] [CrossRef]
- Beibei, X.; Feifei, W.; Diyi, C.; Zhang, H. Hamiltonian modeling of multi-hydro-turbine governing systems with sharing common penstock and dynamic analyses under shock load. Energy Convers. Manag. 2016, 108, 478–487. [Google Scholar]
- Varadhan, S.R.S. Large Deviations and Applications; SIAM: Philadelphia, PA, USA, 1984. [Google Scholar]
- E, W.; Vanden-Eijnden, E. Transition-path theory and path-finding algorithms for the study of rare events. Annu. Rev. Phys. Chem. 2010, 61, 391–420. [Google Scholar] [CrossRef]
- Qi, D.; Majda, A.J. Predicting Fat-Tailed Intermittent Probability Distributions in Passive Scalar Turbulence with Imperfect Models through Empirical Information Theory. Commun. Math. Sci. 2016, 14, 1687–1722. [Google Scholar] [CrossRef]
- Mohamad, M.A.; Sapsis, T.P. Probabilistic Description of Extreme Events in Intermittently Unstable Dynamical Systems Excited by Correlated Stochastic Processes. SIAM/ASA J. Uncertain. Quantif. 2015, 3, 709–736. [Google Scholar] [CrossRef] [Green Version]
- Majda, A.J.; Moore, M.N.J.; Qi, D. Statistical dynamical model to predict extreme events and anomalous features in shallow water waves with abrupt depth change. Proc. Natl. Acad. Sci. USA 2018, 116, 3982–3987. [Google Scholar] [CrossRef]
- Farazmand, M.; Sapsis, T.P. A variational approach to probing extreme events in turbulent dynamical systems. Sci. Adv. 2017, 3, e1701533. [Google Scholar] [CrossRef] [PubMed]
- Wan, Z.Y.; Vlachas, P.R.; Koumoutsakos, P.; Sapsis, T.P. Data-assisted reduced-order modeling of extreme events in complex dynamical systems. PLoS ONE 2018. [Google Scholar] [CrossRef] [PubMed]
- Mohamad, M.A.; Sapsis, T.P. Sequential sampling strategy for extreme event statistics in nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2018, 115, 11138–11143. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Viv Bewick, L.C.; Ball, J. Statistics review 13: Receiver operating characteristic curves. Crit. Care 2004, 8, 508–512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, H.; Garcia, E. Learning from imbalanced data. IEEE Trans. Knowl. Data Eng. 2009, 29, 1263–1284. [Google Scholar]
- Takaya Saito, M.R. The Precision-Recall Plot Is More Informative than the ROC Plot When Evaluating Binary Classifiers on Imbalanced Datasets. PLoS ONE 2015, 10, 1–21. [Google Scholar]
- Cousins, W.; Sapsis, T.P. Reduced-order precursors of rare events in unidirectional nonlinear water waves. J. Fluid Mech. 2016, 790. [Google Scholar] [CrossRef]
- Farazmand, M.; Sapsis, T.P. Reduced-order prediction of rogue waves in two-dimensional deep-water waves. J. Comput. Phys. 2017, 340, 418–434. [Google Scholar] [CrossRef] [Green Version]
- Dematteis, G.; Grafke, T.; Vanden-Eijnden, E. Rogue Waves and Large Deviations in Deep Sea. Proc. Natl. Acad. Sci. USA 2018, 115, 855–860. [Google Scholar] [CrossRef]
- Majda, A.J.; McLaughlin, D.W.; Tabak, E.G. A one-dimensional model for dispersive wave turbulence. J. Nonlinear Sci. 1997, 7, 9–44. [Google Scholar] [CrossRef]
- Platt, N.; Sirovich, L.; Fitzmaurice, N. An investigation of chaotic Kolmogorov flows. Phys. Fluids A 1991, 3, 681–696. [Google Scholar] [CrossRef] [Green Version]
- Cousins, W.; Sapsis, T.P. Quantification and prediction of extreme events in a one-dimensional nonlinear dispersive wave model. Physica D 2014, 280, 48–58. [Google Scholar] [CrossRef]
- Mohamad, M.; Sapsis, T. Probabilistic response and rare events in Mathieu’s equation under correlated parametric excitation. Ocean Eng. 2016, 120. [Google Scholar] [CrossRef]
- Mohamad, M.A.; Cousins, W.; Sapsis, T.P. A probabilistic decomposition-synthesis method for the quantification of rare events due to internal instabilities. J. Comput. Phys. 2016, 322, 288–308. [Google Scholar] [CrossRef] [Green Version]
- David, C.; Andrew, J.; McLaughlin, W.; Esteban, G.T. Dispersive wave turbulence in one dimension. Physica D 2001, 152–153, 551–572. [Google Scholar]
- Benno Rumpf, L.B. Weak turbulence and collapses in the Majda–McLaughlin–Tabak equation: Fluxes in wavenumber and in amplitude space. Physica D 2005, 188–203. [Google Scholar] [CrossRef]
- Gabor, D. Theory of Communication. J. Inst. Electr. Eng. 1946, 93, 429–457. [Google Scholar] [CrossRef]
- Wang, S.; Metcalfe, G.; Stewart, R.L.; Wu, J.; Ohmura, N.; Feng, X.; Yang, C. Solid–liquid separation by particle-flow-instability. Energy Environ. Sci. 2014, 7, 3982–3988. [Google Scholar] [CrossRef]
- Vu, K.K.; D’Ambrosio, C.; Hamadi, Y.; Liberti, L. Surrogate-based methods for black-box optimization. Int. Trans. Oper. Res. 2016, 24. [Google Scholar] [CrossRef]

















© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guth, S.; Sapsis, T.P. Machine Learning Predictors of Extreme Events Occurring in Complex Dynamical Systems. Entropy 2019, 21, 925. https://doi.org/10.3390/e21100925
Guth S, Sapsis TP. Machine Learning Predictors of Extreme Events Occurring in Complex Dynamical Systems. Entropy. 2019; 21(10):925. https://doi.org/10.3390/e21100925
Chicago/Turabian StyleGuth, Stephen, and Themistoklis P. Sapsis. 2019. "Machine Learning Predictors of Extreme Events Occurring in Complex Dynamical Systems" Entropy 21, no. 10: 925. https://doi.org/10.3390/e21100925
APA StyleGuth, S., & Sapsis, T. P. (2019). Machine Learning Predictors of Extreme Events Occurring in Complex Dynamical Systems. Entropy, 21(10), 925. https://doi.org/10.3390/e21100925




