A Class of Association Measures for Categorical Variables Based on Weighted Minkowski Distance
Abstract
:1. Introduction
2. Methods
2.1. A Class of Association Measures for Categorical Variables
2.2. Sample Estimate and Independence Test
2.3. Scaled Forms of Unweighted Measures
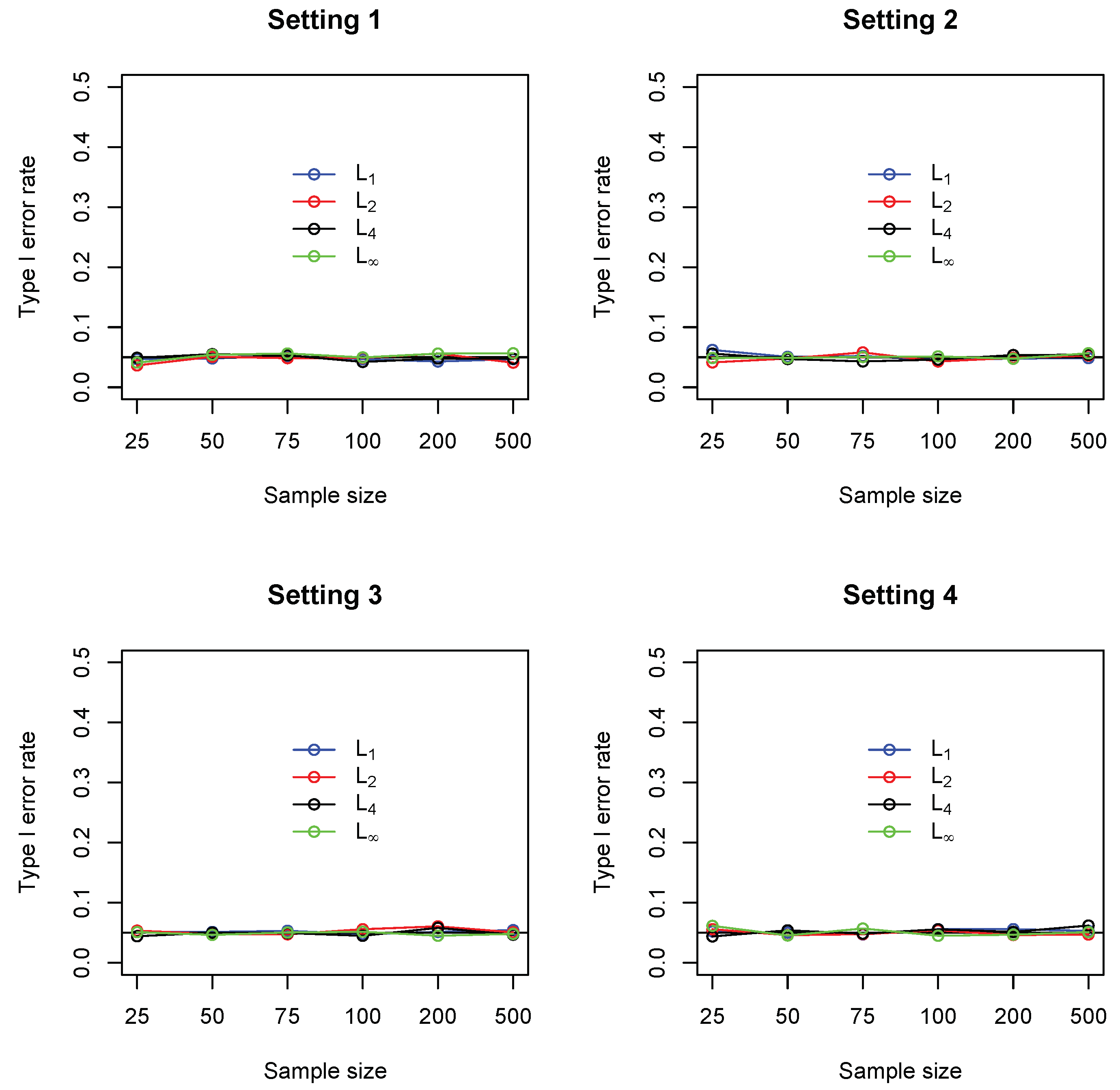
3. Numerical Study
- Setting 1: for 10 randomly selected cells and for the remaining 90 cells
- Setting 2: for 10 randomly selected cells and for the remaining 90 cells
- Setting 3: for one randomly selected cell and for the remaining 99 cells
- Setting 4: for one randomly selected cell and for the remaining 99 cells
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MIC | maximum information coefficient |
| HSIC | Hilbert-Schmidt independence criterion |
| MV | mean variance index |
| c.d.f. | cumulative distribution function |
| p.m.f. | probability mass function |
Appendix A. Technical Details
Appendix A.1. Equivalency between Two Definitions of Distance Covariance
- Definition by Szekely et al. (2007):
- Definition by Sejdinovic et al. (2013):
Appendix A.2. Derivation of Equation (3)
Appendix A.3. Derivation of the Modified Mean Variance Index
Appendix A.4. Proof of Theorem 1
References
- Zhang, Q. Independence test for large sparse contingency tables based on distance correlation. Stat. Probab. Lett. 2019, 148, 17–22. [Google Scholar] [CrossRef]
- Szekely, G.; Rizzo, M.; Bakirov, N. Measuring and testing dependence by correlation of distances. Ann. Stat. 2007, 35, 2769–2794. [Google Scholar] [CrossRef]
- Goodman, L.; Kruskal, W. Measures of association for cross classifications, part I. J. Am. Stat. Assoc. 1954, 49, 732–764. [Google Scholar]
- Cui, H.; Li, R.; Zhong, W. Model-Free Feature Screening for Ultrahigh Dimensional Discriminant Analysis. J. Am. Stat. Assoc. 2015, 110, 630–641. [Google Scholar] [CrossRef] [PubMed]
- Theil, H. On the estimation of relationships involving qualitative variables. Am. J. Sociol. 1970, 76, 103–154. [Google Scholar] [CrossRef]
- McCane, B.; Albert, M. Distance functions for categorical and mixed variables. Pattern Recognit. Lett. 2008, 29, 986–993. [Google Scholar] [CrossRef] [Green Version]
- Reshef, D.; Reshef, Y.; Finucane, H.; Grossman, S.; McVean, P.; Turnbaugh, E.; Lander, M.; Mitzenmacher, M.; Sabeti, P. Detecting novel associations in large data sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef]
- Moews, B.; Herrmann, M.; Ibikunle, G. Lagged correlation-based deep learning for directional trend change prediction in financial time series. arXiv 2018, arXiv:1811.11287. [Google Scholar] [CrossRef]
- Knuth, D. The Art of Computer Programming, 3rd ed.; Addison-Wesley: Boston, MA, USA, 1997. [Google Scholar]
- Cramér, H. Mathematical Methods of Statistics; Princeton Press: Princeton, NJ, USA, 1946. [Google Scholar]
- Tschuprow, A. Principles of the Mathematical Theory of Correlation. Bull. Am. Math. Soc. 1939, 46, 389. [Google Scholar]
- Sejdinovic, D.; Sriperumbudur, B.; Gretton, A.; Fukumizu, K. Equivalence of distance-based and RKHS-based statistics in hypothesis testing. Ann. Stat. 2013, 41, 2263–2291. [Google Scholar] [CrossRef]
- Sriperumbudur, B.; Fukumizu, K.; Gretton, A.; Scholkopf, B.; Lanckriet, G. On the empirical estimation of integral probability metric. Electron. J. Stat. 2012, 6, 1550–1599. [Google Scholar] [CrossRef]
- Zhang, Q.; Tinker, J. Testing conditional independence and homogeneity in large sparse three-way tables using conditional distance covariance. Stat 2019, 8, 1–9. [Google Scholar] [CrossRef]
- Biau, G.; Gyorfi, L. On the asymptotic properties of a nonparametric l1-test statistic of homogeneity. IEEE Trans. Inf. Theory 2005, 51, 3965–3973. [Google Scholar] [CrossRef]


| Y = 1 | Y = 2 | Y = 3 | |
|---|---|---|---|
| X = 1 | 1/2 | 0 | 0 |
| X = 2 | 0 | 1/8 | 1/8 |
| X = 3 | 0 | 1/8 | 1/8 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q. A Class of Association Measures for Categorical Variables Based on Weighted Minkowski Distance. Entropy 2019, 21, 990. https://doi.org/10.3390/e21100990
Zhang Q. A Class of Association Measures for Categorical Variables Based on Weighted Minkowski Distance. Entropy. 2019; 21(10):990. https://doi.org/10.3390/e21100990
Chicago/Turabian StyleZhang, Qingyang. 2019. "A Class of Association Measures for Categorical Variables Based on Weighted Minkowski Distance" Entropy 21, no. 10: 990. https://doi.org/10.3390/e21100990




