No-Signaling-in-Time (NSIT) Condition for Energy
Abstract
:1. Introduction
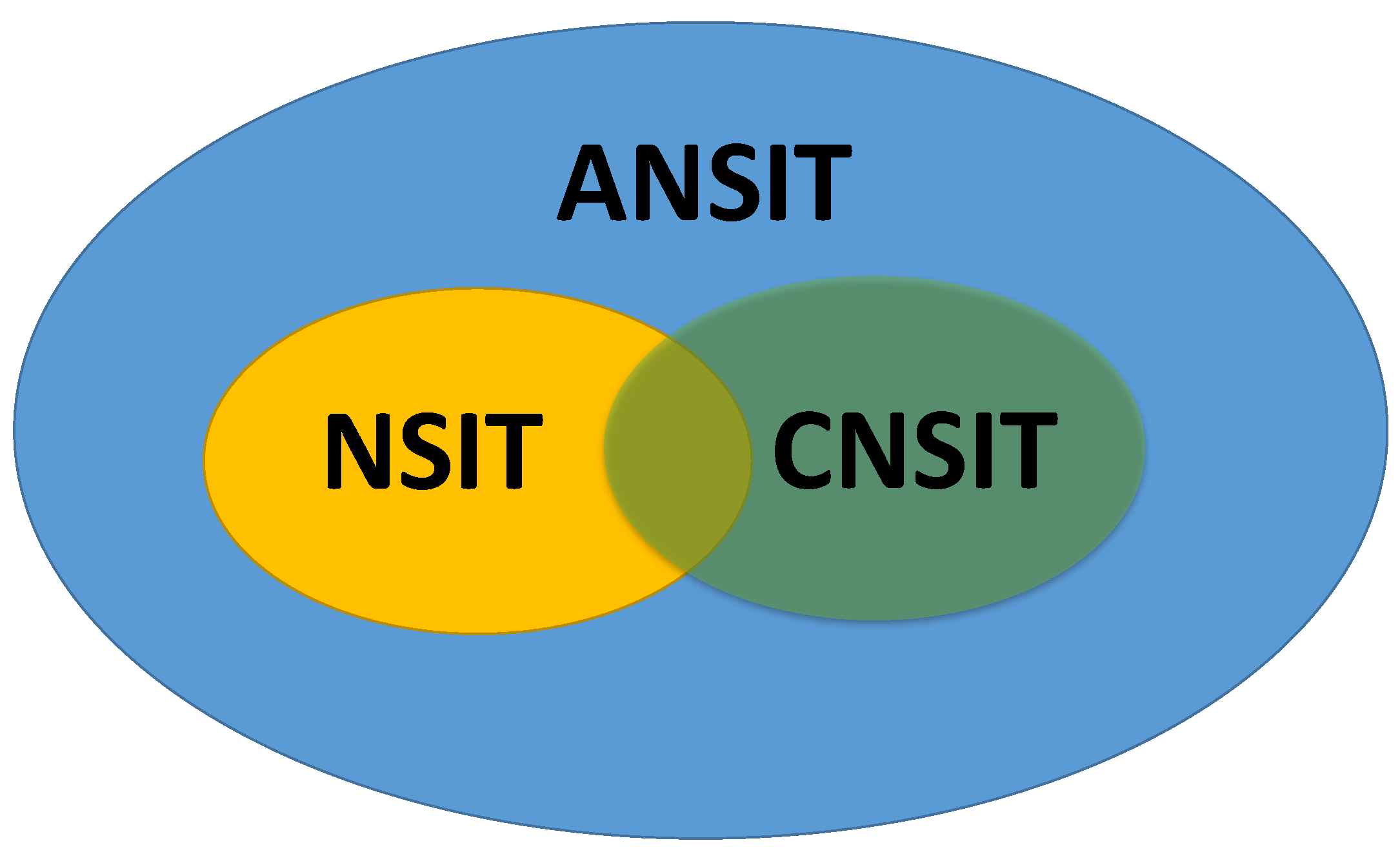
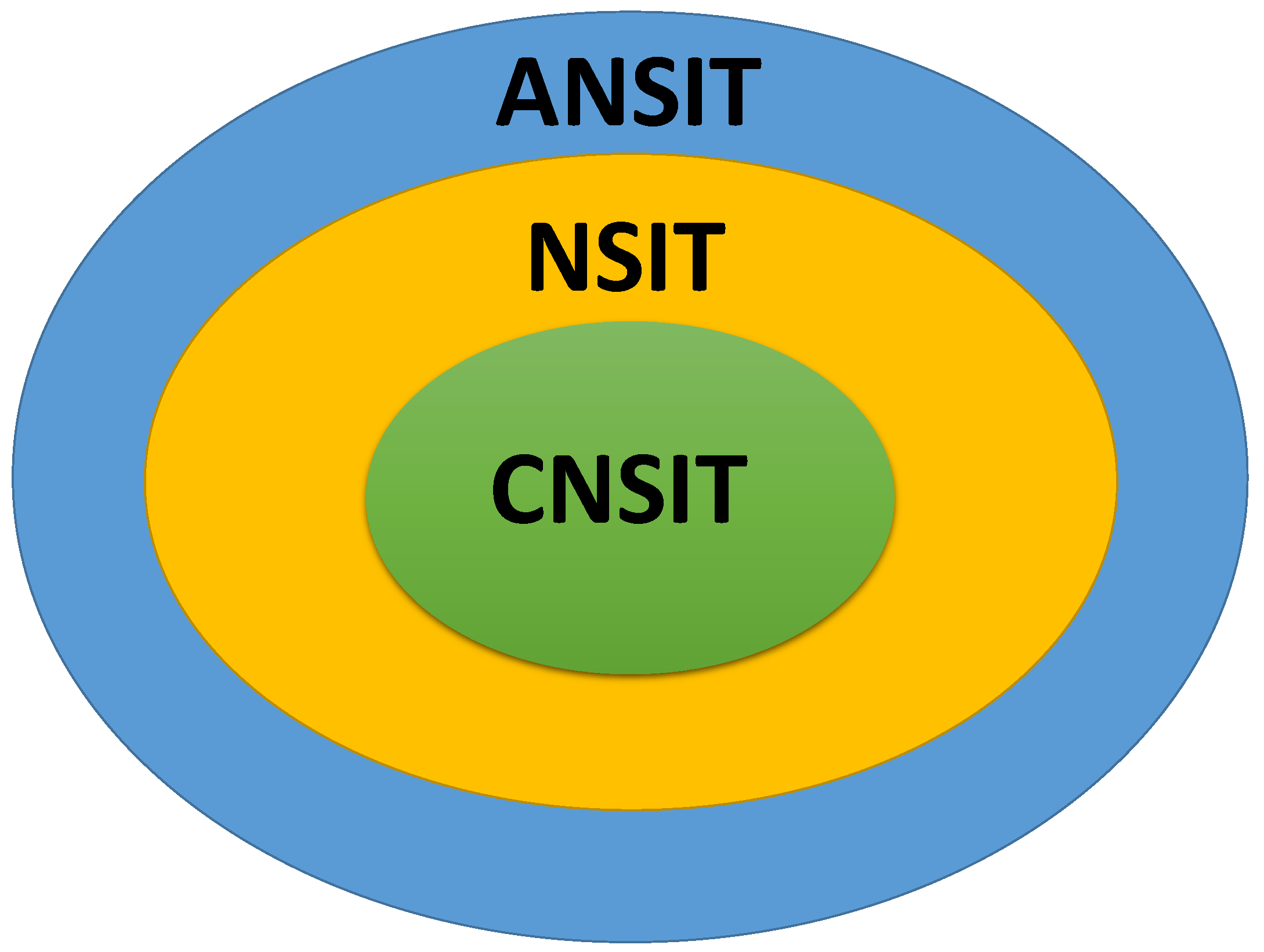
2. NSIT Conditions, CNSIT Conditions and ANSIT Conditions
2.1. Conditional Energy Change
2.2. NSIT Conditions
2.3. CNSIT Conditions
2.4. ANSIT Conditions
3. A Pure Qubit
NSIT Conditions, CNSIT Conditions and ANSIT Conditions for Initial Mixed and Pure States
4. A Driven Qubit
5. A Qubit Interacting with Environment
5.1. A Dissipative Qubit
5.2. A Dephasing Qubit
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| NSIT | no-signaling-in-time |
| CNSIT | no-signaling-in-time conditions for conditional energy |
| ANSIT | no-signaling-in-time conditions for average energy |
| MRps | Macrorealism per se |
| NIM | Non-invasive measurability |
| NS | no-signaling |
| MR | macrorealism |
| CGD | coherence-generating-and-detecting |
Appendix A. ANSIT Conditions
Appendix B. NSIT Conditions for Mixed State under Coherent Dynamics
Appendix C. CNSIT Conditions for Mixed State under Coherent Dynamics
Appendix D. ANSIT Conditions for Mixed State under Coherent Dynamics
References
- Bell, J.S. On the einstein podolsky rosen paradox. Physics 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Leggett, A.; Garg, A. Quantum mechanics versus macroscopic realism: Is the flux there when nobody looks? Phys. Rev. Lett. 1985, 54, 857. [Google Scholar] [CrossRef] [PubMed]
- Leggett, A.J. Testing the limits of quantum mechanics: Motivation, state of play, prospects. J. Phys. Condens. Matter 2002, 14, R415. [Google Scholar] [CrossRef]
- Leggett, A.J. Realism and the physical world. Rep. Prog. Phys. 2008, 71, 022001. [Google Scholar] [CrossRef]
- Palacios-Laloy, A.; Mallet, F.; Nguyen, F.; Bertet, P.; Vion, D.; Esteve, D.; Korotkov, A.N. Experimental violation of a Bell’s inequality in time with weak measurement. Nat. Phys. 2010, 6, 442–447. [Google Scholar] [CrossRef]
- Dressel, J.; Broadbent, C.J.; Howell, J.C.; Jordan, A.N. Experimental Violation of Two-Party Leggett–Garg Inequalities with Semiweak Measurements. Phys. Rev. Lett. 2011, 106, 040402. [Google Scholar] [CrossRef] [PubMed]
- Goggin, M.E.; Almeida, M.P.; Barbieri, M.; Lanyon, B.P.; O’Brien, J.L.; White, A.G.; Pryde, G.J. Violation of the Leggett–Garg inequality with weak measurements of photons. Proc. Natl. Acad. Sci. USA 2011, 108, 1256–1261. [Google Scholar] [CrossRef]
- Knee, G.C.; Simmons, S.; Gauger, E.M.; Morton, J.J.L.; Riemann, H.; Abrosimov, N.V.; Becker, P.; Pohl, H.J.; Itoh, K.M.; Thewalt, M.L.W.; et al. Violation of a Leggett–Garg inequality with ideal non-invasive measurements. Nat. Commun. 2012, 3, 606. [Google Scholar] [CrossRef]
- Zhou, Z.Q.; Huelga, S.F.; Li, C.F.; Guo, G.C. Experimental Detection of Quantum Coherent Evolution through the Violation of Leggett–Garg-Type Inequalities. Phys. Rev. Lett. 2015, 115, 113002. [Google Scholar] [CrossRef]
- Robens, C.; Alt, W.; Meschede, D.; Emary, C.; Alberti, A. Ideal negative measurements in quantum walks disprove theories based on classical trajectories. Phys. Rev. X 2015, 5, 011003. [Google Scholar] [CrossRef]
- Paz, J.P.; Mahler, G. Proposed test for temporal Bell inequalities. Phys. Rev. Lett. 1993, 71, 3235. [Google Scholar] [CrossRef] [PubMed]
- Kofler, J.; Brukner, Č. Condition for macroscopic realism beyond the Leggett–Garg inequalities. Phys. Rev. A 2013, 87, 052115. [Google Scholar] [CrossRef]
- Clemente, L.; Kofler, J. Necessary and sufficient conditions for macroscopic realism from quantum mechanics. Phys. Rev. A 2015, 91, 062103. [Google Scholar] [CrossRef]
- Clemente, L.; Kofler, J. No fine theorem for macrorealism: Limitations of the Leggett–Garg inequality. Phys. Rev. Lett. 2016, 116, 150401. [Google Scholar] [CrossRef] [PubMed]
- Li, C.M.; Lambert, N.; Chen, Y.N.; Chen, G.Y.; Nori, F. Witnessing quantum coherence: from solid-state to biological systems. Sci. Rep. 2012, 2, 885. [Google Scholar] [CrossRef] [PubMed]
- Kumari, S.; Pan, A.K. Probing various formulations of macrorealism for unsharp quantum measurements. Phys. Rev. A 2017, 96, 042107. [Google Scholar] [CrossRef] [Green Version]
- Chanda, T.; Das, T.; Mal, S.; Sen, A.; Sen, U. Canonical Leggett–Garg inequality: Nonclassicality of temporal quantum correlations under energy constraint. Phys. Rev. A 2018, 98, 022138. [Google Scholar] [CrossRef]
- Seifert, U. Entropy Production Along a Stochastic Trajectory and an Integral Fluctuation Theorem. Phys. Rev. Lett. 2005, 95, 040602. [Google Scholar] [CrossRef]
- Sekimoto, K. Stochastic Energetics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Jarzynski, C. Equalities and inequalities: Irreversibility and the second law of thermodynamics at the nanoscale. Annu. Rev. Condens. Matter Phys. 2011, 2, 329. [Google Scholar] [CrossRef]
- Mohammady, M.H.; Romito, A. Conditional work statistics of quantum measurements. Quantum 2019, 3, 175. [Google Scholar] [CrossRef]
- Horowitz, J.M. Quantum-trajectory approach to the stochastic thermodynamics of a forced harmonic oscillator. Phys. Rev. E 2012, 85, 031110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hekking, F.W.J.; Pekola, J.P. Quantum jump approach for work and dissipation in a two-level system. Phys. Rev. Lett. 2013, 111, 093602. [Google Scholar] [CrossRef] [PubMed]
- Alonso, J.J.; Lutz, E.; Romito, A. Thermodynamics of weakly measured quantum systems. Phys. Rev. Lett. 2016, 116, 080403. [Google Scholar] [CrossRef] [PubMed]
- Elouard, C.; Herrera-Martí, D.A.; Clusel, M.; Auffèves, A. The role of quantum measurement in stochastic thermodynamics. Quantum Inf. 2017, 3, 9. [Google Scholar] [CrossRef]
- Naghiloo, M.; Tan, D.; Harrington, P.M.; Alonso, J.J.; Lutz, E.; Romito, A.; Murch, K.W. Thermodynamics along individual trajectories of a quantum bit. arXiv 2017, arXiv:1703.05885. [Google Scholar]
- Naghiloo, M.; Alonso, J.J.; Romito, A.; Lutz, E.; Murch, K.W. Information gain and loss for a quantum maxwell’s demon. Phys. Rev. Lett. 2018, 121, 030604. [Google Scholar] [CrossRef]
- Elouard, C.; Mohammady, M.H. Work, heat and entropy production along quantum trajectories. Thermodynamics in the Quantum Regime; Springer International Publishing: Cham, Switzerland, 2018; Volume 195, pp. 363–393. [Google Scholar]
- Maroney, O.J.E.; Timpson, C.G. Quantum-vs. macro-realism: What does the Leggett–Garg inequality actually test? arXiv 2014, arXiv:1412.6139. [Google Scholar]
- Smirne, A.; Egloff, D.; Díaz, M.G.; Plenio, M.B.; Huelga, S.F. Coherence and non-classicality of quantum Markov processes. Quantum Sci. Technol. 2019, 4, 01LT01. [Google Scholar] [CrossRef]
- Louisell, W.H. Radiation and Noise in Quantum Electronics; McGraw-Hill: San Francisco, NC, USA, 1964. [Google Scholar]
- Vedral, V. Modern Foundations of Quantum Optics; Imperial College Press: London, UK, 2005. [Google Scholar]

| coherent dynamics | mixed state | pure state |
| NSIT conditions | 1. 2. 3. and | |
| CNSIT conditions | 1. | |
| 1. | 2. and | |
| 2. | 3. and | |
| 4. and | ||
| 5. and | ||
| ANSIT conditions | 1. | |
| 1. | 2. | |
| 2. | 3. ; | |
| 3. ; | 4. , and ; | |
| 4. | 5., and ; | |
| 6. , and ; | ||
| 7. , and ; | ||
| dynamics under dissipation | ||
| NSIT conditions | 1. 2. and 3. and | |
| CNSIT conditions | ||
| ANSIT conditions | 1. 2. | |
| dynamics under dephasing | ||
| NSIT conditions | 1. 2. and 3. and | |
| CNSIT conditions | 1. | |
| 1. | 2. and | |
| 2. | 3. and | |
| 4. and | ||
| 5. and | ||
| ANSIT conditions | 1. | |
| 2. ; | ||
| 3. , and ; | ||
| 1. | 4. , and ; | |
| 2. ; | 5. , and ; | |
| 3. | 6. , and ; | |
| 7. , and ; | ||
| 8. , and ; | ||
| 9. , and ; | ||
| 10. , and ; | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zou, J.; Shao, B. No-Signaling-in-Time (NSIT) Condition for Energy. Entropy 2019, 21, 1067. https://doi.org/10.3390/e21111067
Zhang Y, Zou J, Shao B. No-Signaling-in-Time (NSIT) Condition for Energy. Entropy. 2019; 21(11):1067. https://doi.org/10.3390/e21111067
Chicago/Turabian StyleZhang, Yuxia, Jian Zou, and Bin Shao. 2019. "No-Signaling-in-Time (NSIT) Condition for Energy" Entropy 21, no. 11: 1067. https://doi.org/10.3390/e21111067
APA StyleZhang, Y., Zou, J., & Shao, B. (2019). No-Signaling-in-Time (NSIT) Condition for Energy. Entropy, 21(11), 1067. https://doi.org/10.3390/e21111067





