Dynamical Behavior of β-Lactamases and Penicillin- Binding Proteins in Different Functional States and Its Potential Role in Evolution
Abstract
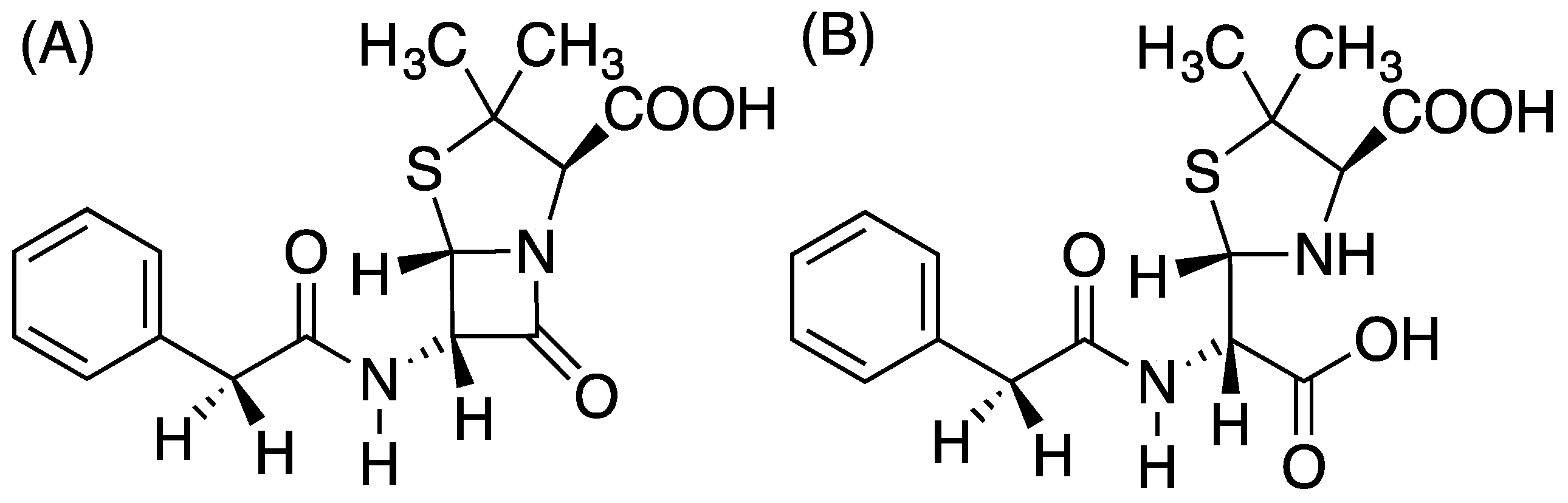
:1. Introduction
2. Materials and Methods
2.1. Molecular Dynamic Simulations
2.2. Root-Mean-Square Fluct+uation (RMSF)
2.3. Principal Component Analysis (PCA)
2.4. Configurational Entropy
2.5. Time-Structure-Based Independent Component Analysis (t-ICA)
2.6. Markov State Models (MSMs)
2.7. Hidden Markov Model (HMM)
2.8. Transition-Path Theory
3. Results
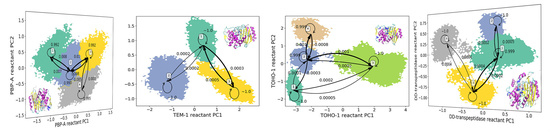
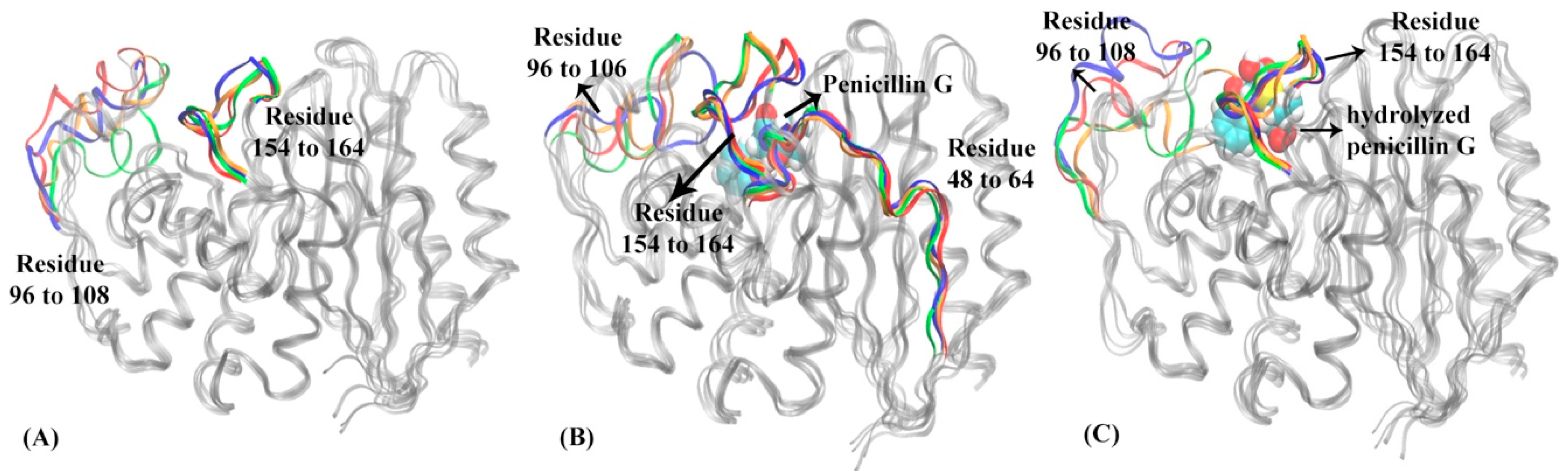
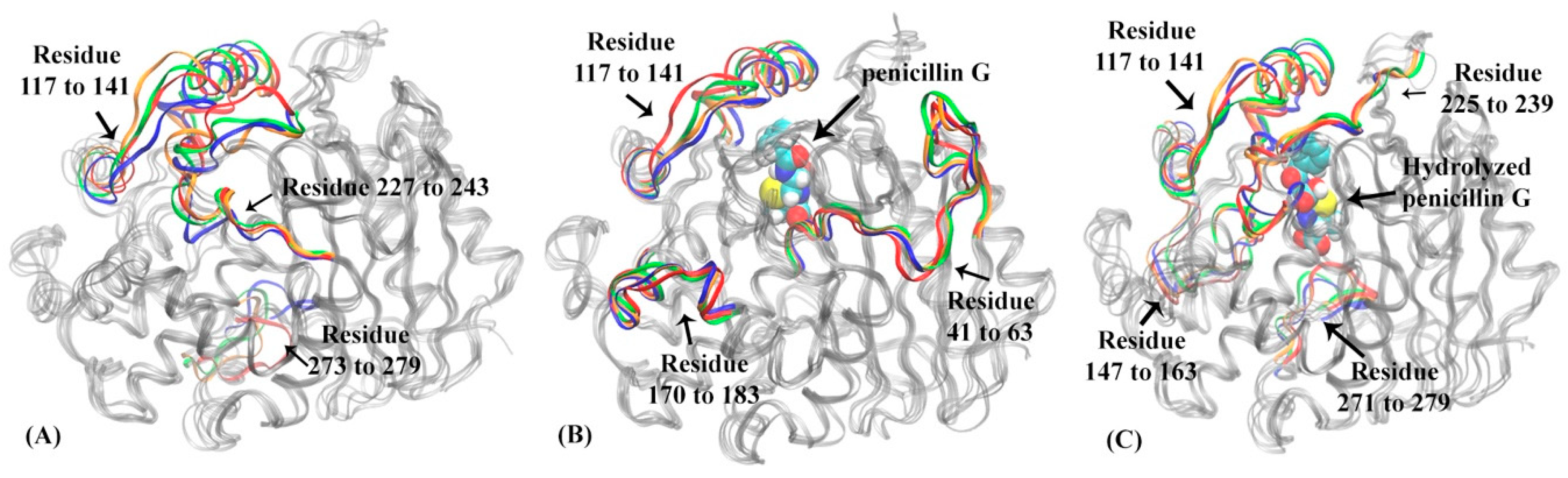
3.1. Hidden Markov State Models Analysis of Overall Structures
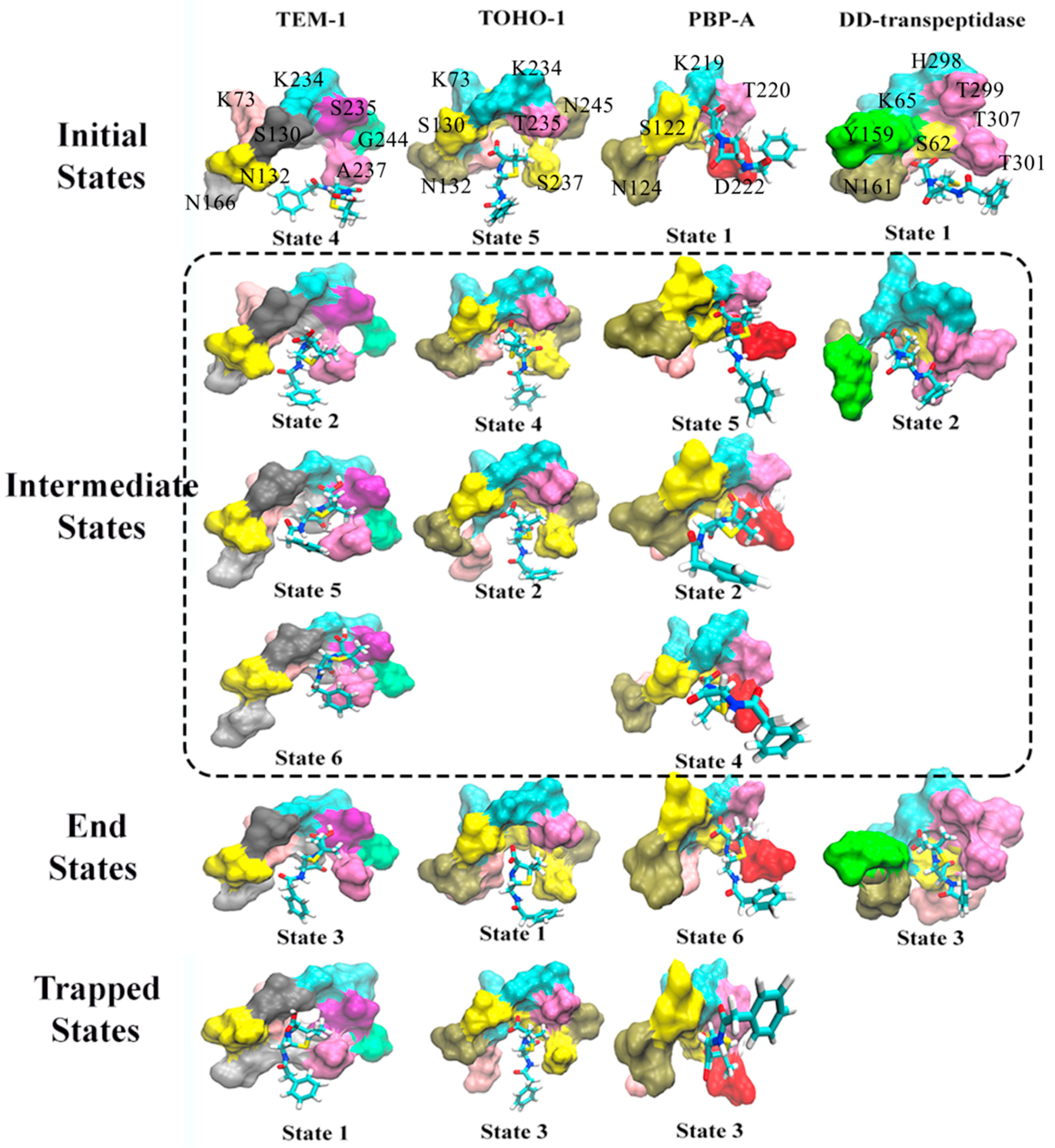
3.2. Analysis of Active Site Structures Using Markov State Models
3.3. Atomic Distance
3.4. Configurational Entropy
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hall, B.G.; Barlow, M. Evolution of the serine β-lactamases: Past, present and future. Drug Resist. Updates 2004, 7, 111–123. [Google Scholar] [CrossRef] [PubMed]
- Coates, A.; Hu, Y.; Bax, R.; Page, C. The future challenges facing the development of new antimicrobial drugs. Nat. Rev. Drug Discov. 2002, 1, 895–910. [Google Scholar] [CrossRef] [PubMed]
- Medeiros, A.A. Evolution and Dissemination of β-Lactamases Accelerated by Generations of β-Lactam Antibiotics. Clin. Infect. Dis. 1997, 24, S19–S45. [Google Scholar] [CrossRef] [PubMed]
- Strynadka, N.C.J.; Adachi, H.; Jensen, S.E.; Johns, K.; Sielecki, A.; Betzel, C.; Sutoh, K.; James, M.N.G. Molecular structure of the acyl-enzyme intermediate in β-lactam hydrolysis at 1.7 Å resolution. Nature 1992, 359, 700–705. [Google Scholar] [CrossRef]
- Shimamura, T.; Ibuka, A.; Fushinobu, S.; Wakagi, T.; Ishiguro, M.; Ishii, Y.; Matsuzawa, H. Acyl-intermediate Structures of the Extended-spectrum Class A β-Lactamase, Toho-1, in Complex with Cefotaxime, Cephalothin, and Benzylpenicillin. J. Biol. Chem. 2002, 277, 46601–46608. [Google Scholar] [CrossRef]
- Tomanicek, S.J.; Blakeley, M.P.; Cooper, J.; Chen, Y.; Afonine, P.V.; Coates, L. Neutron Diffraction Studies of a Class A β-Lactamase Toho-1 E166A/R274N/R276N Triple Mutant. J. Mol. Biol. 2010, 396, 1070–1080. [Google Scholar] [CrossRef]
- Tomanicek, S.J.; Standaert, R.F.; Weiss, K.L.; Ostermann, A.; Schrader, T.E.; Ng, J.D.; Coates, L. Neutron and X-ray Crystal Structures of a Perdeuterated Enzyme Inhibitor Complex Reveal the Catalytic Proton Network of the Toho-1 β-Lactamase for the Acylation Reaction. J. Biol. Chem. 2013, 288, 4715–4722. [Google Scholar] [CrossRef]
- Vandavasi, V.G.; Weiss, K.L.; Cooper, J.B.; Erskine, P.T.; Tomanicek, S.J.; Ostermann, A.; Schrader, T.E.; Ginell, S.L.; Coates, L. Exploring the Mechanism of β-Lactam Ring Protonation in the Class A β-lactamase Acylation Mechanism Using Neutron and X-ray Crystallography. J. Med. Chem. 2016, 59, 474–479. [Google Scholar] [CrossRef]
- Ibuka, A.; Taguchi, A.; Ishiguro, M.; Fushinobu, S.; Ishii, Y.; Kamitori, S.; Okuyama, K.; Yamaguchi, K.; Konno, M.; Matsuzawa, H. Crystal structure of the E166A mutant of extended-spectrum β-lactamase toho-1 at 1.8 Å resolution11Edited by R. Huber. J. Mol. Biol. 1999, 285, 2079–2087. [Google Scholar] [CrossRef]
- Ibuka, A.S.; Ishii, Y.; Galleni, M.; Ishiguro, M.; Yamaguchi, K.; Frère, J.-M.; Matsuzawa, H.; Sakai, H. Crystal Structure of Extended-Spectrum β-Lactamase Toho-1: Insights into the Molecular Mechanism for Catalytic Reaction and Substrate Specificity Expansion. Biochemistry 2003, 42, 10634–10643. [Google Scholar] [CrossRef]
- Shimizu-Ibuka, A.; Matsuzawa, H.; Sakai, H. An Engineered Disulfide Bond between Residues 69 and 238 in Extended-Spectrum β-Lactamase Toho-1 Reduces Its Activity toward Third-Generation Cephalosporins. Biochemistry 2004, 43, 15737–15745. [Google Scholar] [CrossRef] [PubMed]
- Kelly, J.A.; Dideberg, O.; Charlier, P.; Wery, J.P.; Libert, M.; Moews, P.C.; Knox, J.R.; Duez, C.; Fraipont, C.; Joris, B.; et al. On the origin of bacterial resistance to penicillin: Comparison of a beta-lactamase and a penicillin target. Science 1986, 231, 1429. [Google Scholar] [CrossRef] [PubMed]
- Urbach, C.; Evrard, C.; Pudzaitis, V.; Fastrez, J.; Soumillion, P.; Declercq, J.-P. Structure of PBP-A from Thermosynechococcus elongatus, a Penicillin-Binding Protein Closely Related to Class A β-Lactamases. J. Mol. Biol. 2009, 386, 109–120. [Google Scholar] [CrossRef]
- Pratt, R.F. β-Lactamases: Why and How. J. Med. Chem. 2016, 59, 8207–8220. [Google Scholar] [CrossRef] [PubMed]
- Silvaggi, N.R.; Josephine, H.R.; Kuzin, A.P.; Nagarajan, R.; Pratt, R.F.; Kelly, J.A. Crystal Structures of Complexes between the R61 DD-peptidase and Peptidoglycan-mimetic β-Lactams: A Non-covalent Complex with a “Perfect Penicillin” This article is dedicated to the memory of Professor Jean-Marie Ghuysen of the Université de Liège, Belgium, in recognition of his decades of contributions towards our understanding of and ability to combat bacterial infections. J. Mol. Biol. 2005, 345, 521–533. [Google Scholar] [CrossRef] [PubMed]
- Wilkin, J.M.; Dubus, A.; Joris, B.; Frère, J.M. The mechanism of action of DD-peptidases: The role of Threonine-299 and -301 in the Streptomyces R61 DD-peptidase. Biochem. J 1994, 301, 477. [Google Scholar] [CrossRef] [PubMed]
- Tipper, D.J.; Strominger, J.L. Mechanism of action of penicillins: A proposal based on their structural similarity to acyl-D-alanyl-D-alanine. Proc. Natl. Acad. Sci. USA 1965, 54, 1133. [Google Scholar] [CrossRef]
- Cheng, F.; Liu, C.; Jiang, J.; Lu, W.; Li, W.; Liu, G.; Zhou, W.; Huang, J.; Tang, Y. Prediction of Drug-Target Interactions and Drug Repositioning via Network-Based Inference. PLoS Comp. Biol. 2012, 8, e1002503. [Google Scholar] [CrossRef]
- Öztürk, H.; Ozkirimli, E.; Özgür, A. Classification of Beta-Lactamases and Penicillin Binding Proteins Using Ligand-Centric Network Models. PLoS ONE 2015, 10, e0117874. [Google Scholar] [CrossRef]
- Urbach, C.; Fastrez, J.; Soumillion, P. A New Family of Cyanobacterial Penicillin-binding Proteins: A MISSING LINK IN THE EVOLUTION OF CLASS A β-LACTAMASES. J. Biol. Chem. 2008, 283, 32516–32526. [Google Scholar] [CrossRef]
- Hargis, J.C.; White, J.K.; Chen, Y.; Woodcock, H.L. Can Molecular Dynamics and QM/MM Solve the Penicillin Binding Protein Protonation Puzzle? J. Chem. Inf. Model. 2014, 54, 1412–1424. [Google Scholar] [CrossRef] [PubMed]
- Gherman, B.F.; Goldberg, S.D.; Cornish, V.W.; Friesner, R.A. Mixed Quantum Mechanical/Molecular Mechanical (QM/MM) Study of the Deacylation Reaction in a Penicillin Binding Protein (PBP) versus in a Class C β-Lactamase. J. Am. Chem. Soc. 2004, 126, 7652–7664. [Google Scholar] [CrossRef] [PubMed]
- Pratt, R.F. Functional evolution of the serine β-lactamase active site. J. Chem. Soc. Perk. Trans. 2 2002, 851–861. [Google Scholar] [CrossRef]
- Noé, F.; Schütte, C.; Vanden-Eijnden, E.; Reich, L.; Weikl, T.R. Constructing the equilibrium ensemble of folding pathways from short off-equilibrium simulations. Proc. Natl. Acad. Sci. USA 2009, 106, 19011. [Google Scholar] [CrossRef] [PubMed]
- Noé, F.; Wu, H.; Prinz, J.-H.; Plattner, N. Projected and hidden Markov models for calculating kinetics and metastable states of complex molecules. J. Chem. Phys. 2013, 139, 184114. [Google Scholar] [CrossRef]
- Wang, F.; Shen, L.; Zhou, H.; Wang, S.; Wang, X.; Tao, P. Machine Learning Classification Model for Functional Binding Modes of TEM-1 β-Lactamase. Front. Mol. Biosci. 2019, 6, 47. [Google Scholar] [CrossRef]
- Best, R.B.; Zhu, X.; Shim, J.; Lopes, P.E.; Mittal, J.; Feig, M.; MacKerell, A.D., Jr. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone ϕ, ψ and side-chain χ1 and χ2 dihedral angles. J. Chem. Theory Comput. 2012, 8, 3257–3273. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef]
- Yu, W.; He, X.; Vanommeslaeghe, K.; MacKerell, A.D., Jr. Extension of the CHARMM general force field to sulfonyl-containing compounds and its utility in biomolecular simulations. J. Comput. Chem. 2012, 33, 2451–2468. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Neria, E.; Fischer, S.; Karplus, M. Simulation of activation free energies in molecular systems. J. Chem. Phys. 1996, 105, 1902–1921. [Google Scholar] [CrossRef]
- Ryckaert, J.-P.; Ciccotti, G.; Berendsen, H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef] [Green Version]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N log (N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef] [Green Version]
- Friedrichs, M.S.; Eastman, P.; Vaidyanathan, V.; Houston, M.; Legrand, S.; Beberg, A.L.; Ensign, D.L.; Bruns, C.M.; Pande, V.S. Accelerating molecular dynamic simulation on graphics processing units. J. Comput. Chem. 2009, 30, 864–872. [Google Scholar] [CrossRef] [PubMed]
- Eastman, P.; Pande, V. OpenMM: A hardware-independent framework for molecular simulations. Comput. Sci. Eng. 2010, 12, 34–39. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eastman, P.; Swails, J.; Chodera, J.D.; McGibbon, R.T.; Zhao, Y.; Beauchamp, K.A.; Wang, L.-P.; Simmonett, A.C.; Harrigan, M.P.; Stern, C.D. OpenMM 7: Rapid development of high performance algorithms for molecular dynamics. PLoS Comp. Biol. 2017, 13, e1005659. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Zhou, H.; Olademehin, O.P.; Kim, S.J.; Tao, P. Insights into Key Interactions between Vancomycin and Bacterial Cell Wall Structures. ACS Omega 2018, 3, 37–45. [Google Scholar] [CrossRef]
- Jolliffe, I. Principal component analysis. In International Encyclopedia of Statistical Science; Springer: New York, NY, USA, 2011; pp. 1094–1096. [Google Scholar]
- Levy, R.M.; Srinivasan, A.R.; Olson, W.K.; McCammon, J.A. Quasi-harmonic method for studying very low frequency modes in proteins. Biopolymers 1984, 23, 1099–1112. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, F.; Tao, P. t-Distributed Stochastic Neighbor Embedding Method with the Least Information Loss for Macromolecular Simulations. J. Chem. Theory Comput. 2018, 14, 5499–5510. [Google Scholar] [CrossRef]
- Schwantes, C.R.; Pande, V.S. Improvements in Markov State Model Construction Reveal Many Non-Native Interactions in the Folding of NTL9. J. Chem. Theory Comput. 2013, 9, 2000–2009. [Google Scholar] [CrossRef] [Green Version]
- Pérez-Hernández, G.; Paul, F.; Giorgino, T.; De Fabritiis, G.; Noé, F. Identification of slow molecular order parameters for Markov model construction. J. Chem. Phys. 2013, 139, 015102. [Google Scholar] [CrossRef] [PubMed]
- Naritomi, Y.; Fuchigami, S. Slow dynamics in protein fluctuations revealed by time-structure based independent component analysis: The case of domain motions. J. Chem. Phys. 2011, 134, 065101. [Google Scholar] [CrossRef] [PubMed]
- Pinamonti, G.; Zhao, J.; Condon, D.E.; Paul, F.; Noè, F.; Turner, D.H.; Bussi, G. Predicting the Kinetics of RNA Oligonucleotides Using Markov State Models. J. Chem. Theory Comput. 2017, 13, 926–934. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Plattner, N.; Noé, F. Protein conformational plasticity and complex ligand-binding kinetics explored by atomistic simulations and Markov models. Nat. Commun. 2015, 6, 7653. [Google Scholar] [CrossRef] [Green Version]
- Chodera, J.D.; Elms, P.; Noé, F.; Keller, B.; Kaiser, C.M.; Ewall-Wice, A.; Marqusee, S.; Bustamante, C.; Hinrichs, N.S. Bayesian hidden Markov model analysis of single-molecule force spectroscopy: Characterizing kinetics under measurement uncertainty. arXiv 2011, arXiv:1108.1430. [Google Scholar]
- Trendelkamp-Schroer, B.; Wu, H.; Paul, F.; Noé, F. Estimation and uncertainty of reversible Markov models. J. Chem. Phys. 2015, 143, 174101. [Google Scholar] [CrossRef]
- Vanden-Eijnden, E. Transition Path Theory. In An Introduction to Markov State Models and Their Application to Long Timescale Molecular Simulation; Bowman, G.R., Pande, V.S., Noé, F., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 91–100. [Google Scholar] [CrossRef]
- David, C.C.; Jacobs, D.J. Principal Component Analysis: A Method for Determining the Essential Dynamics of Proteins. In Protein Dynamics: Methods and Protocols; Livesay, D.R., Ed.; Humana Press: Totowa, NJ, USA, 2014; pp. 193–226. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Yu, Z.-G.; Anh, V. Cluster protein structures using recurrence quantification analysis on coordinates of alpha-carbon atoms of proteins. Phys. Lett. A 2007, 368, 314–319. [Google Scholar] [CrossRef] [Green Version]
- Webber, C.L., Jr.; Giuliani, A.; Zbilut, J.P.; Colosimo, A. Elucidating protein secondary structures using alpha-carbon recurrence quantifications. Proteins Struct. Funct. Bioinform. 2001, 44, 292–303. [Google Scholar] [CrossRef]
- Scherer, M.K.; Trendelkamp-Schroer, B.; Paul, F.; Pérez-Hernández, G.; Hoffmann, M.; Plattner, N.; Wehmeyer, C.; Prinz, J.-H.; Noé, F. PyEMMA 2: A Software Package for Estimation, Validation, and Analysis of Markov Models. J. Chem. Theory Comput. 2015, 11, 5525–5542. [Google Scholar] [CrossRef]
- Rabiner, L.R. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar] [CrossRef]
- Baum, L.E.; Petrie, T.; Soules, G.; Weiss, N. A Maximization Technique Occurring in the Statistical Analysis of Probabilistic Functions of Markov Chains. Ann. Math. Stat. 1970, 41, 164–171. [Google Scholar] [CrossRef]
- Russell, R.B.; Barton, G.J. Multiple protein sequence alignment from tertiary structure comparison: Assignment of global and residue confidence levels. Proteins Struct. Funct. Bioinform. 1992, 14, 309–323. [Google Scholar] [CrossRef] [PubMed]
- Donoghue, P.; Luthey-Schulten, Z. On the Evolution of Structure in Aminoacyl-tRNA Synthetases. Microbiol. Mol. Biol. Rev. 2003, 67, 550. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hermann, J.C.; Hensen, C.; Ridder, L.; Mulholland, A.J.; Höltje, H.-D. Mechanisms of Antibiotic Resistance: QM/MM Modeling of the Acylation Reaction of a Class A β-Lactamase with Benzylpenicillin. J. Am. Chem. Soc. 2005, 127, 4454–4465. [Google Scholar] [CrossRef]
- Castillo, R.; Silla, E.; Tuñón, I. Role of Protein Flexibility in Enzymatic Catalysis: Quantum Mechanical−Molecular Mechanical Study of the Deacylation Reaction in Class A β-Lactamases. J. Am. Chem. Soc. 2002, 124, 1809–1816. [Google Scholar] [CrossRef] [PubMed]
- Swarén, P.; Maveyraud, L.; Raquet, X.; Cabantous, S.; Duez, C.; Pédelacq, J.-D.; Mariotte-Boyer, S.; Mourey, L.; Labia, R.; Nicolas-Chanoine, M.-H. X-ray analysis of the NMC-A β-lactamase at 1.64-Å resolution, a class A carbapenemase with broad substrate specificity. J. Biol. Chem. 1998, 273, 26714–26721. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Díaz, N.; Suárez, D.; Sordo, T.L.; Merz, K.M. Acylation of class A β-lactamases by penicillins: A theoretical examination of the role of serine 130 and the β-lactam carboxylate group. J Phys. Chem. B 2001, 105, 11302–11313. [Google Scholar] [CrossRef]
- Noé, F.; Horenko, I.; Schütte, C.; Smith, J.C. Hierarchical analysis of conformational dynamics in biomolecules: Transition networks of metastable states. J. Chem. Phys. 2007, 126, 155102. [Google Scholar] [CrossRef]
- Bös, F.; Pleiss, J. Multiple Molecular Dynamics Simulations of TEM β-Lactamase: Dynamics and Water Binding of the Ω-Loop. Biophys. J. 2009, 97, 2550–2558. [Google Scholar] [CrossRef] [Green Version]
- Fisette, O.; Morin, S.; Savard, P.-Y.; Lagüe, P.; Gagné, S.M. TEM-1 Backbone Dynamics—Insights from Combined Molecular Dynamics and Nuclear Magnetic Resonance. Biophys. J. 2010, 98, 637–645. [Google Scholar] [CrossRef] [Green Version]
- Horn, J.R.; Shoichet, B.K. Allosteric Inhibition through Core Disruption. J. Mol. Biol. 2004, 336, 1283–1291. [Google Scholar] [CrossRef] [PubMed]
- Matagne, A.; Lamotte-Brasseur, J.; FrÈRe, J.-M. Catalytic properties of class A β-lactamases: Efficiency and diversity. Biochem. J. 1998, 330, 581. [Google Scholar] [CrossRef] [PubMed]
- Imtiaz, U.; Billings, E.; Knox, J.R.; Manavathu, E.K.; Lerner, S.A.; Mobashery, S. Inactivation of class A. beta.-lactamases by clavulanic acid: The role of arginine-244 in a proposed nonconcerted sequence of events. J. Am. Chem. Soc. 1993, 115, 4435–4442. [Google Scholar] [CrossRef]
- Shimizu-Ibuka, A.; Oishi, M.; Yamada, S.; Ishii, Y.; Mura, K.; Sakai, H.; Matsuzawa, H. Roles of Residues Cys69, Asn104, Phe160, Gly232, Ser237, and Asp240 in Extended-Spectrum β-Lactamase Toho-1. Antimicrob. Agents Chemother. 2011, 55, 284. [Google Scholar] [CrossRef] [Green Version]
- Langan, P.S.; Vandavasi, V.G.; Cooper, S.J.; Weiss, K.L.; Ginell, S.L.; Parks, J.M.; Coates, L. Substrate Binding Induces Conformational Changes in a Class A β-lactamase That Prime It for Catalysis. ACS Catalysis 2018, 8, 2428–2437. [Google Scholar] [CrossRef]
- Doucet, N.; Savard, P.-Y.; Pelletier, J.N.; Gagné, S.M. NMR Investigation of Tyr105 Mutants in TEM-1 β-Lactamase: DYNAMICS ARE CORRELATED WITH FUNCTION. J. Biol. Chem. 2007, 282, 21448–21459. [Google Scholar] [CrossRef] [Green Version]
- McDonough, M.A.; Anderson, J.W.; Silvaggi, N.R.; Pratt, R.F.; Knox, J.R.; Kelly, J.A. Structures of Two Kinetic Intermediates Reveal Species Specificity of Penicillin-binding Proteins. J. Mol. Biol. 2002, 322, 111–122. [Google Scholar] [CrossRef]
- Silvaggi, N.R.; Anderson, J.W.; Brinsmade, S.R.; Pratt, R.F.; Kelly, J.A. The Crystal Structure of Phosphonate-Inhibited d-Ala-d-Ala Peptidase Reveals an Analogue of a Tetrahedral Transition State. Biochemistry 2003, 42, 1199–1208. [Google Scholar] [CrossRef]

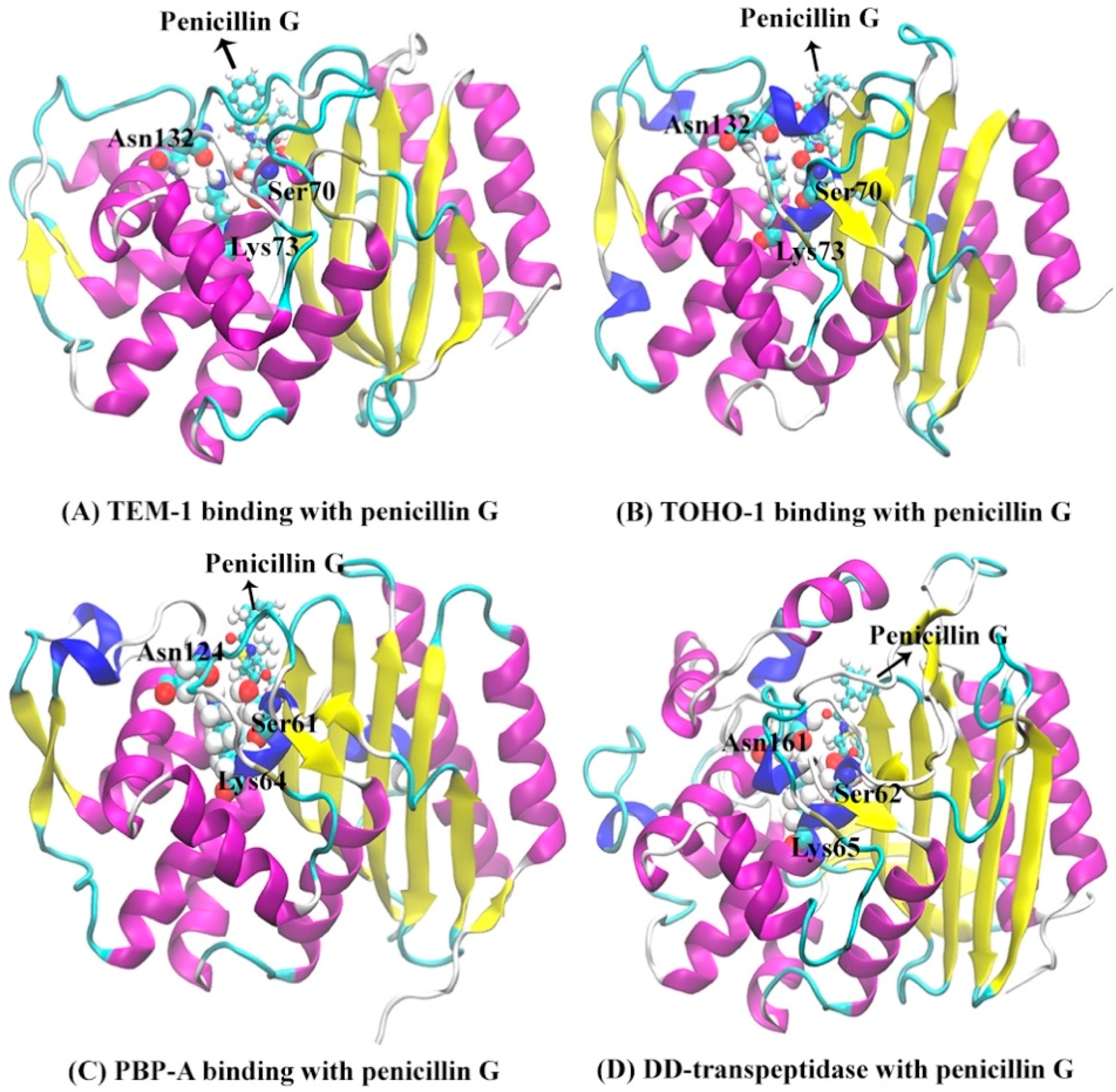









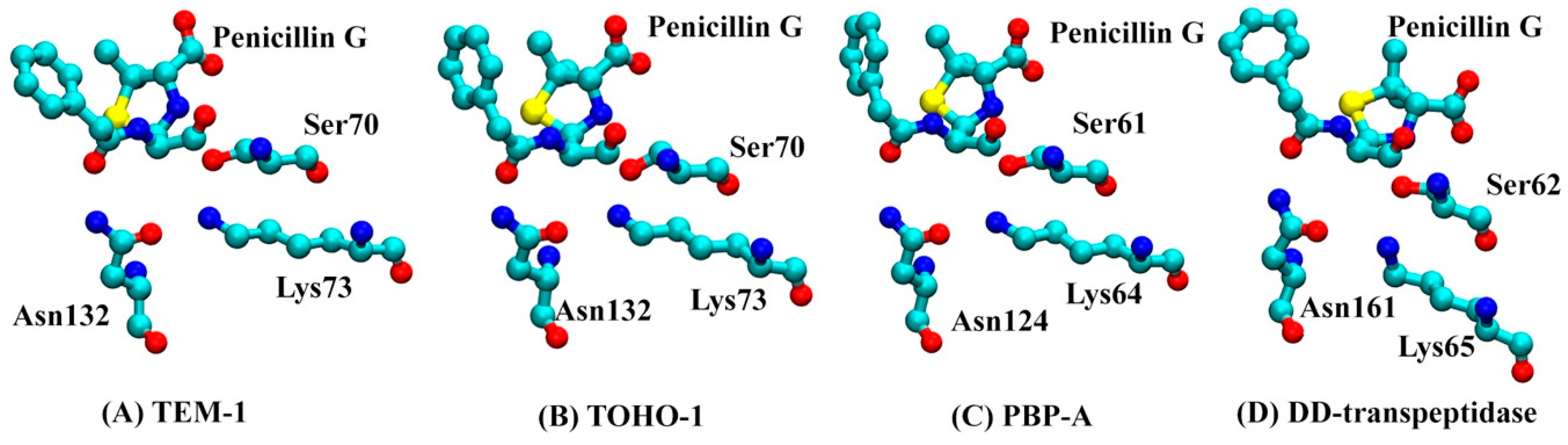

| TEM-1 | TOHO-1 | PBP-A | DD-Transpeptidase |
|---|---|---|---|
| S70 | S70 | S61 | S62 |
| K73 | K73 | K64 | K65 |
| S130 | S130 | S122 | Y159 |
| N132 | N132 | N124 | N161 |
| N166 | A166 | L158 | A237 |
| K234 | K234 | K219 | H298 |
| S235 | T235 | T220 | T299 |
| A237 | S237 | D222 | T301 |
| G244 | N245 | G228 | T307 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Zhou, H.; Wang, X.; Tao, P. Dynamical Behavior of β-Lactamases and Penicillin- Binding Proteins in Different Functional States and Its Potential Role in Evolution. Entropy 2019, 21, 1130. https://doi.org/10.3390/e21111130
Wang F, Zhou H, Wang X, Tao P. Dynamical Behavior of β-Lactamases and Penicillin- Binding Proteins in Different Functional States and Its Potential Role in Evolution. Entropy. 2019; 21(11):1130. https://doi.org/10.3390/e21111130
Chicago/Turabian StyleWang, Feng, Hongyu Zhou, Xinlei Wang, and Peng Tao. 2019. "Dynamical Behavior of β-Lactamases and Penicillin- Binding Proteins in Different Functional States and Its Potential Role in Evolution" Entropy 21, no. 11: 1130. https://doi.org/10.3390/e21111130
APA StyleWang, F., Zhou, H., Wang, X., & Tao, P. (2019). Dynamical Behavior of β-Lactamases and Penicillin- Binding Proteins in Different Functional States and Its Potential Role in Evolution. Entropy, 21(11), 1130. https://doi.org/10.3390/e21111130