Natural Convection and Irreversibility Evaluation in a Cubic Cavity with Partial Opening in Both Top and Bottom Sides
Abstract
:1. Introduction
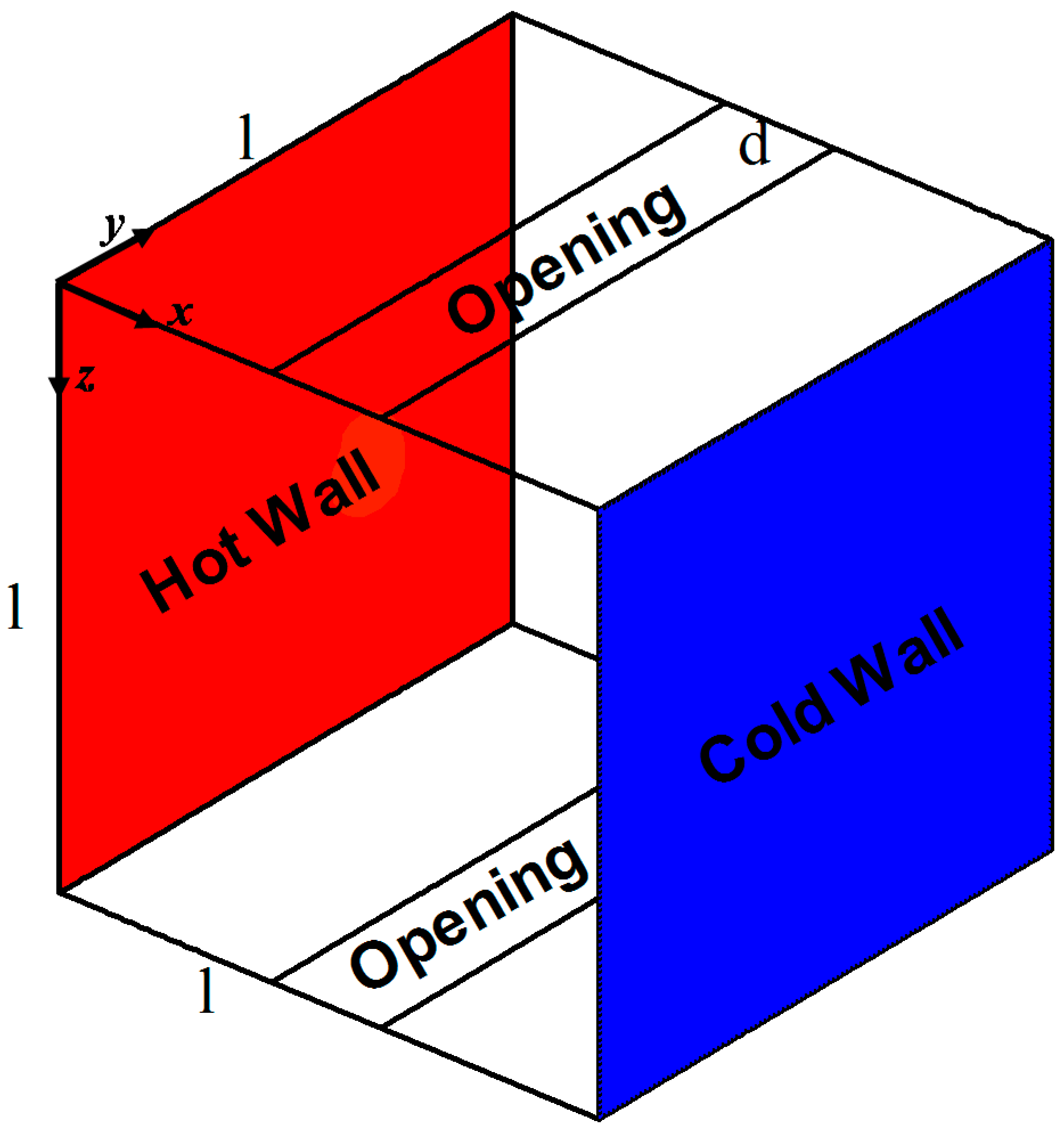
2. Physical Model
3. Mathematical Formulation
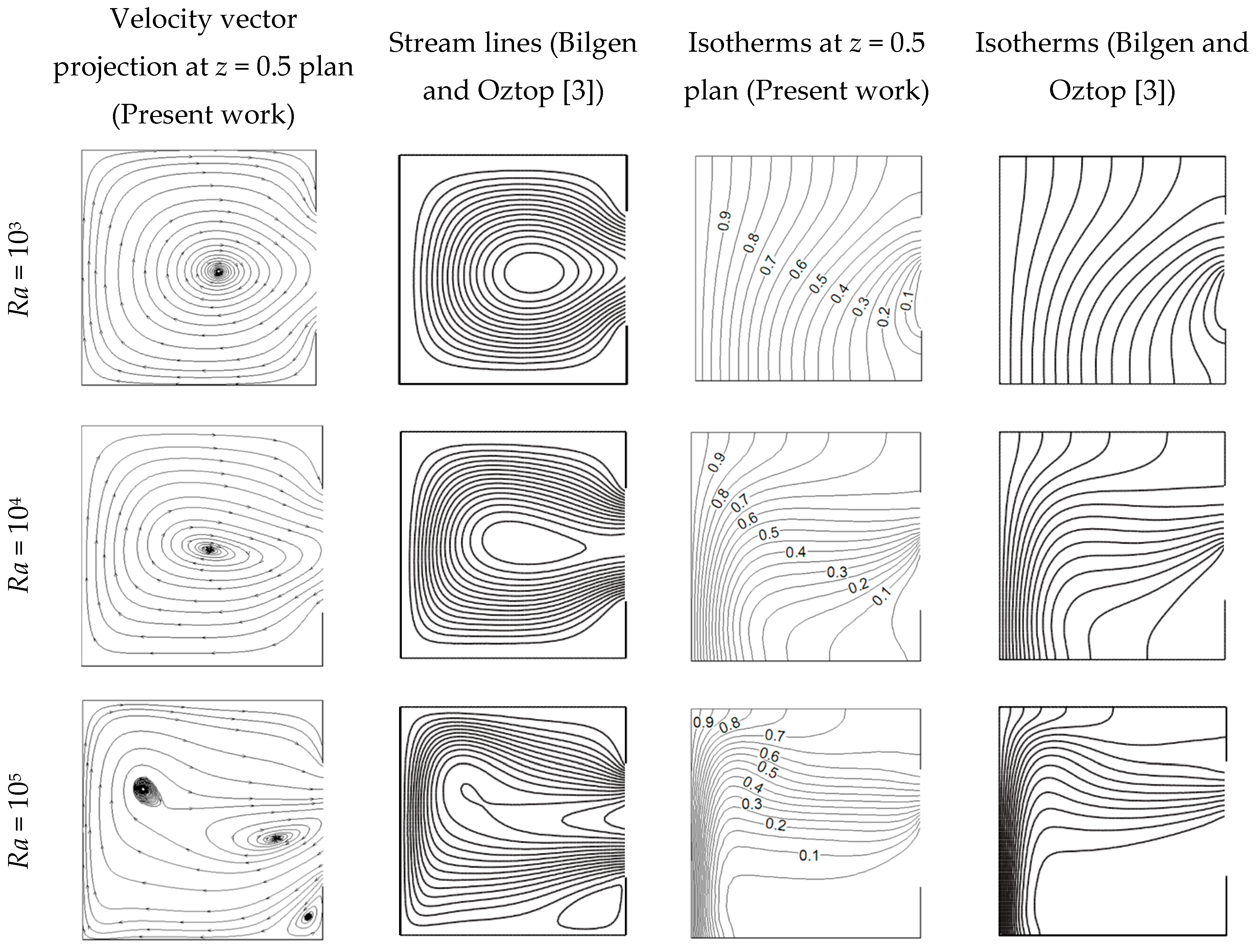
4. Verification and Grid Sensitive Study
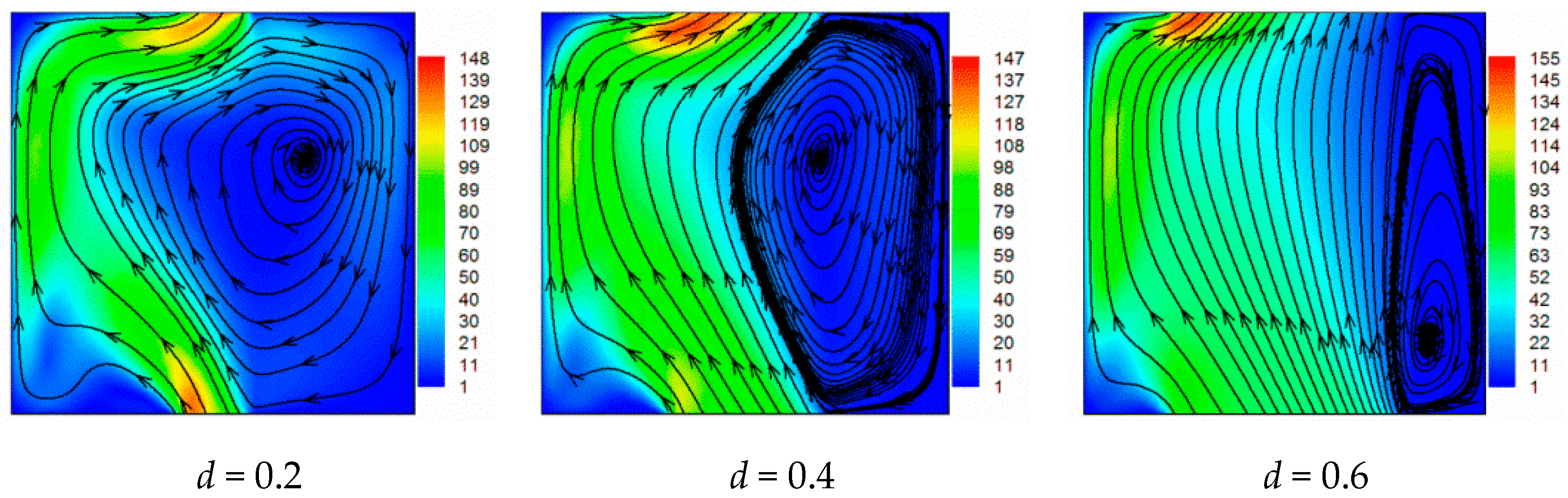
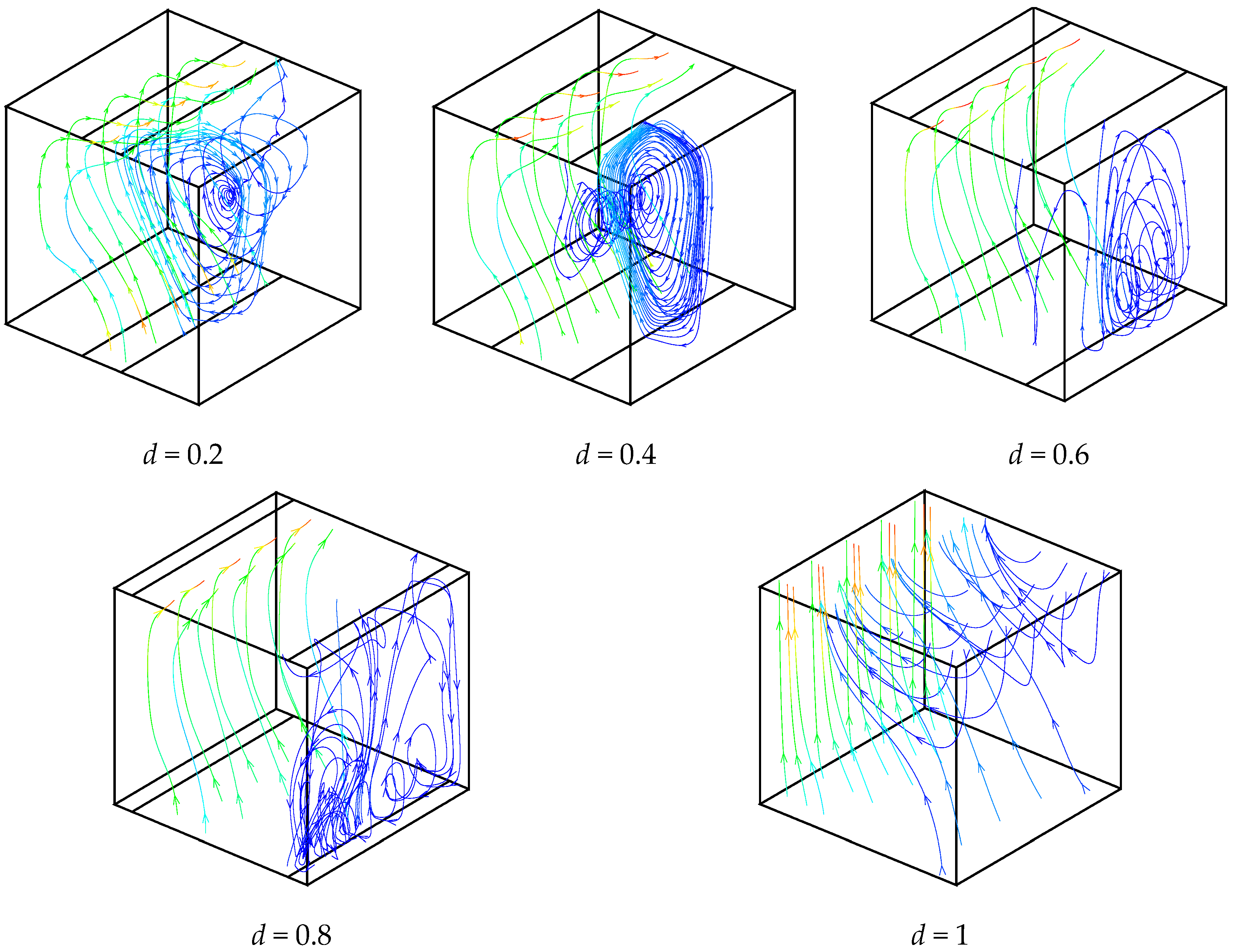
5. Results and Discussion
6. Conclusions
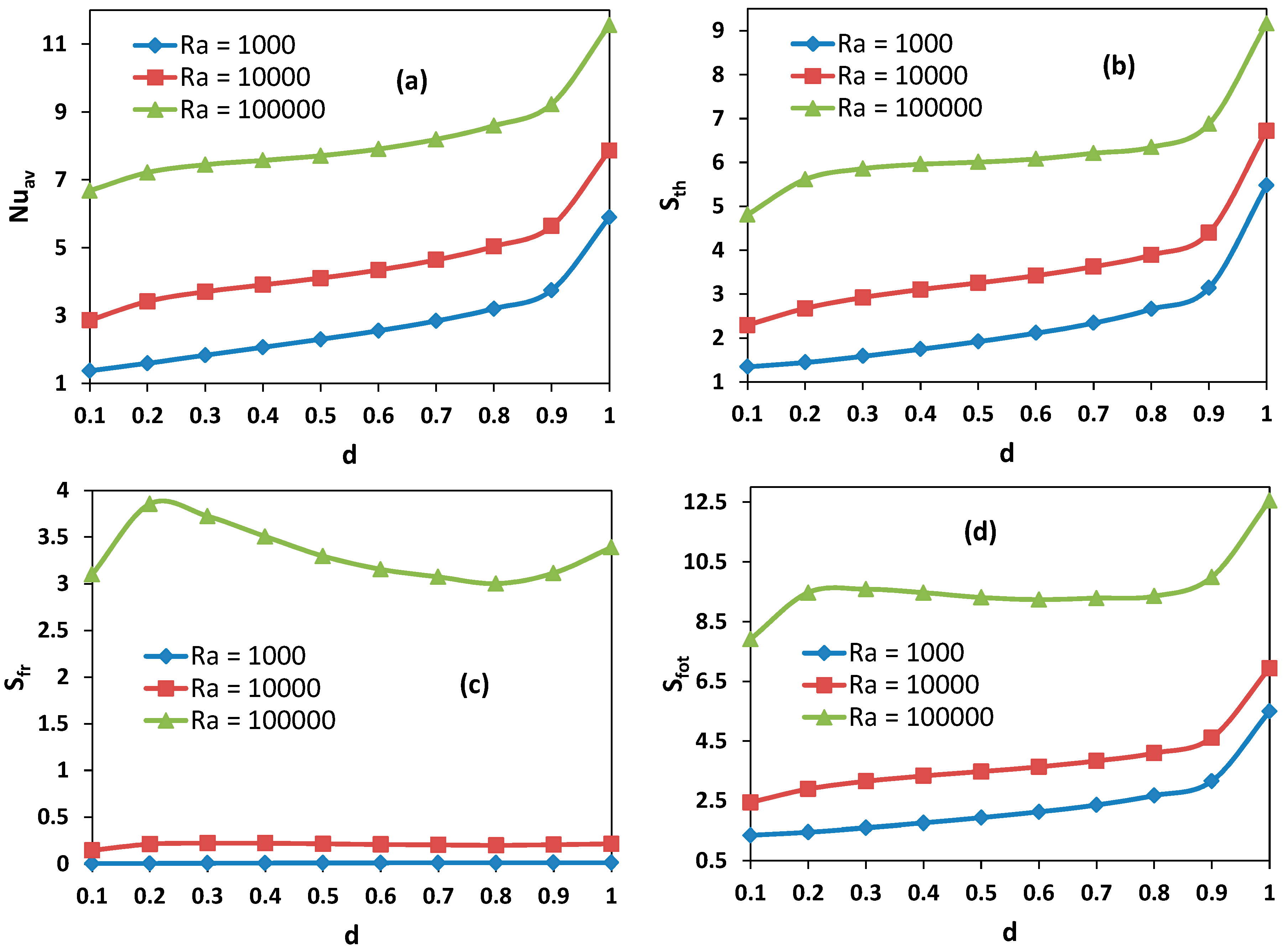
- Heat transfer enhances with increasing the opening ratios and Rayleigh numbers.
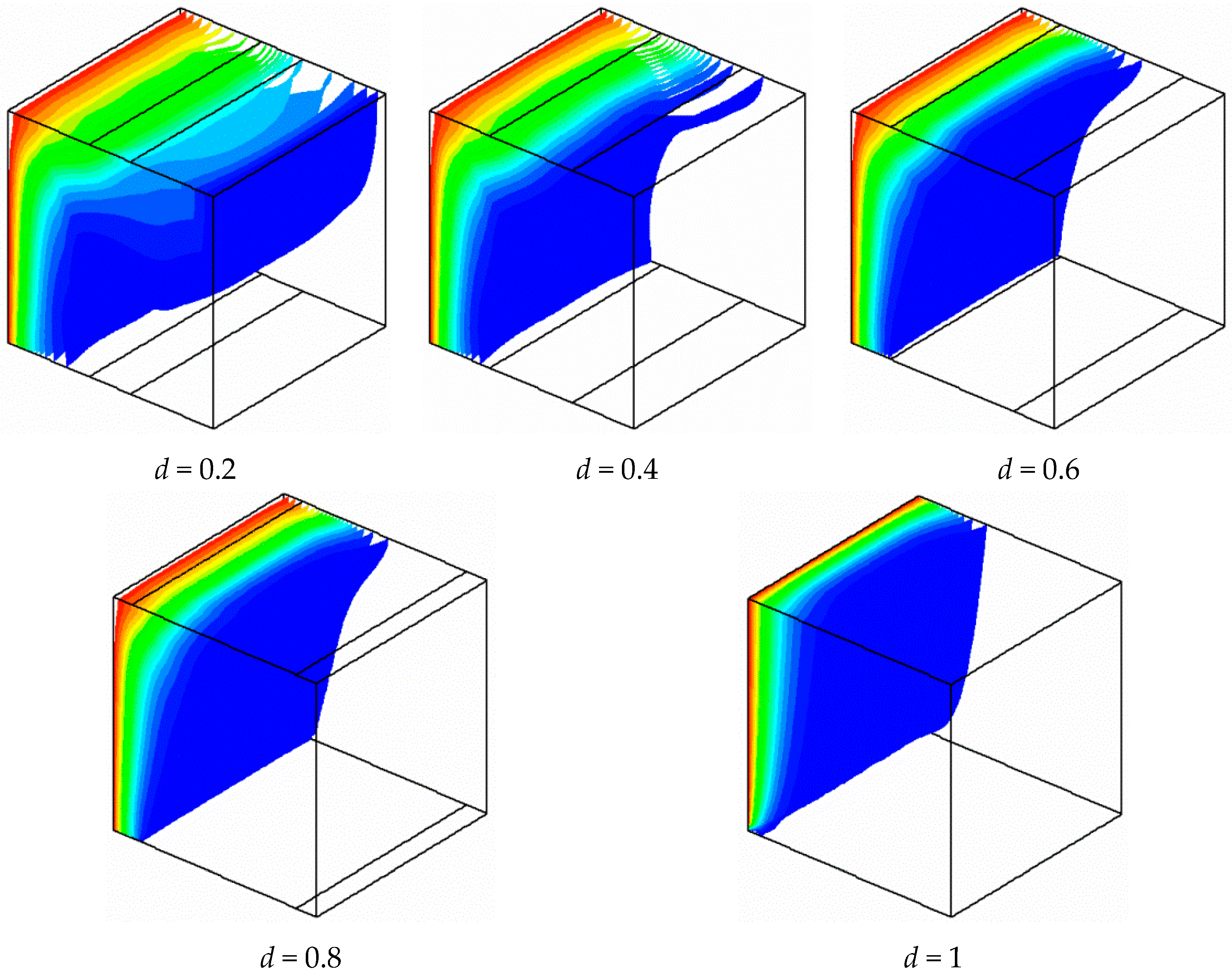
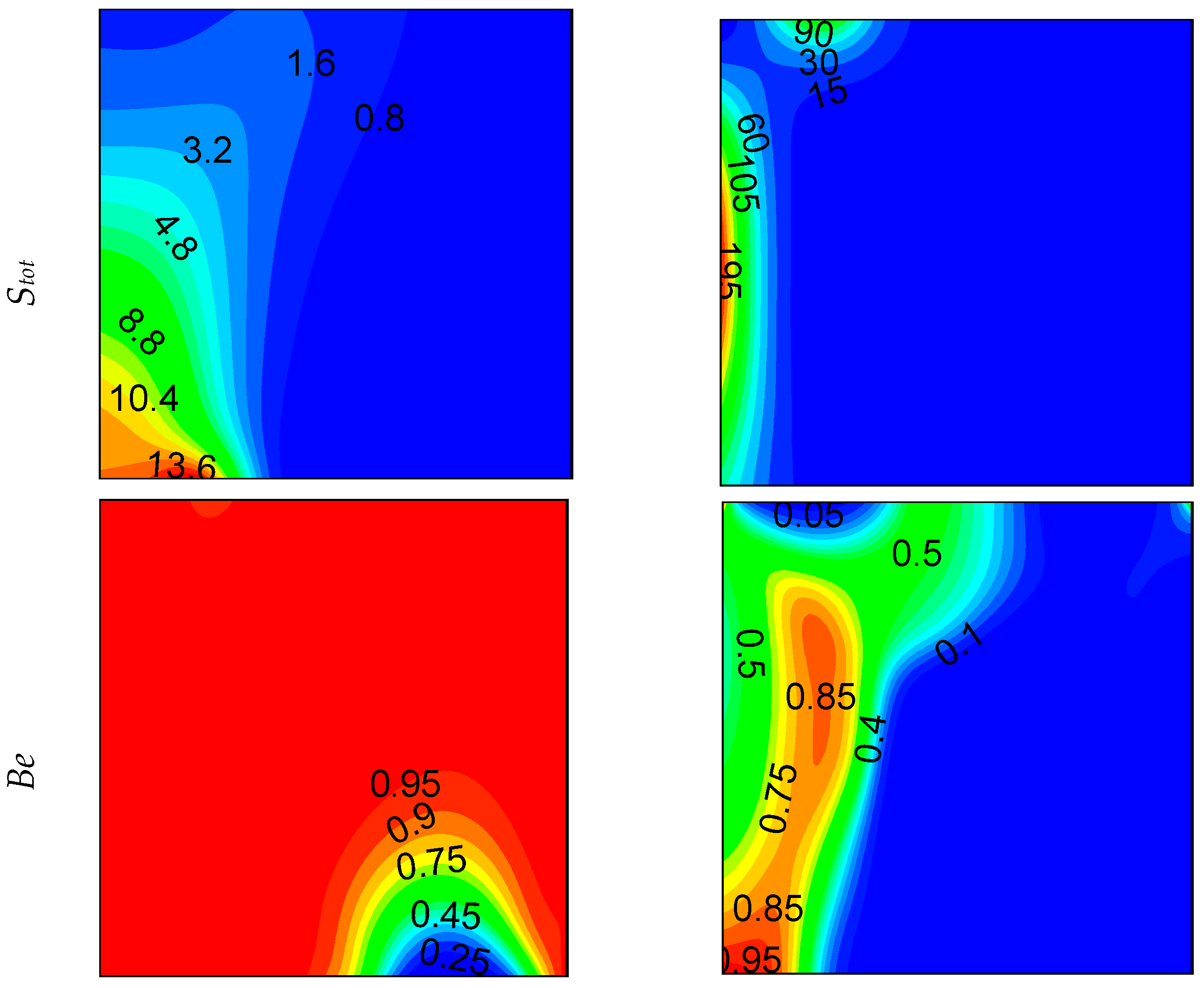
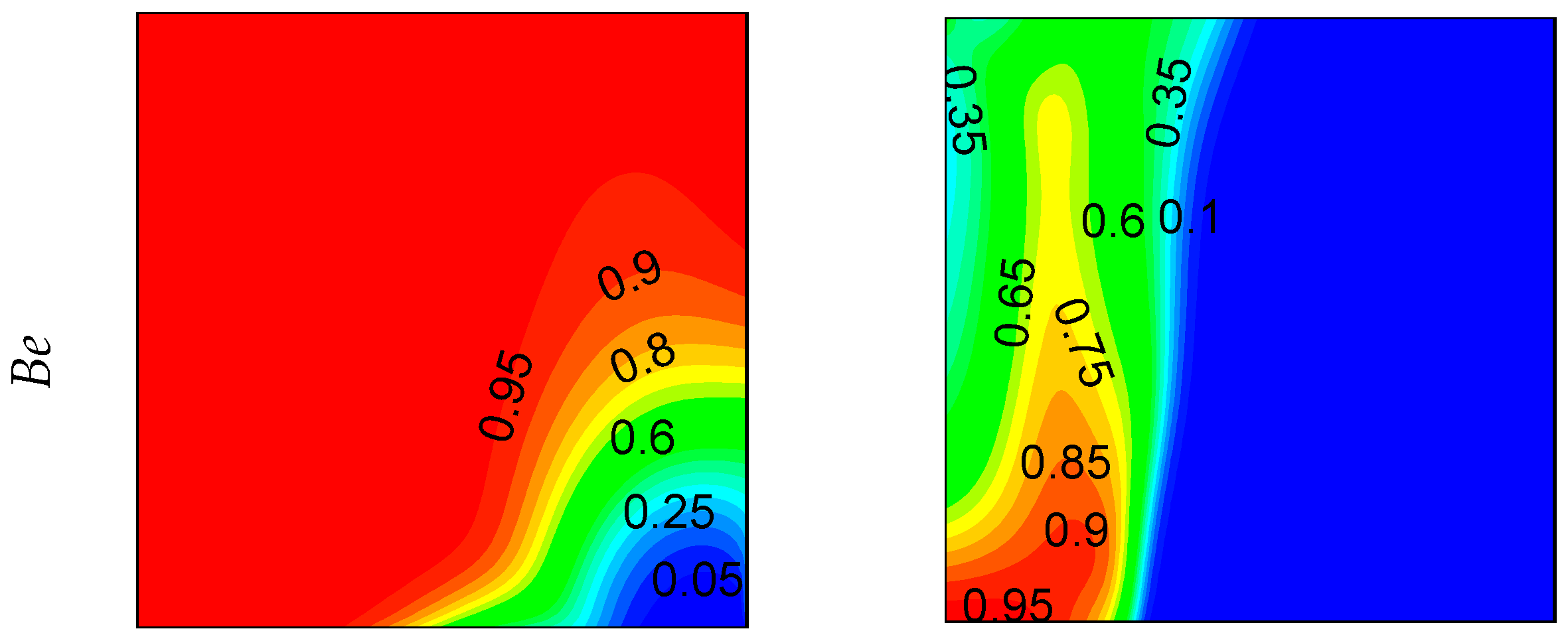
- The flow field can be controlled in a cavity with the width of opening part. Both the dimension and location of circulation cells can be controlled.
- The novelty of this work was to undertake an analysis of the natural cooling and natural ventilation problem of a model room. Thus, the results can be used for building ventilation.
- As expected, the flow is more pronounced near of heated part compared to other regions.
- The obtained results can be used for some kinds of filters or heating and cooling systems.
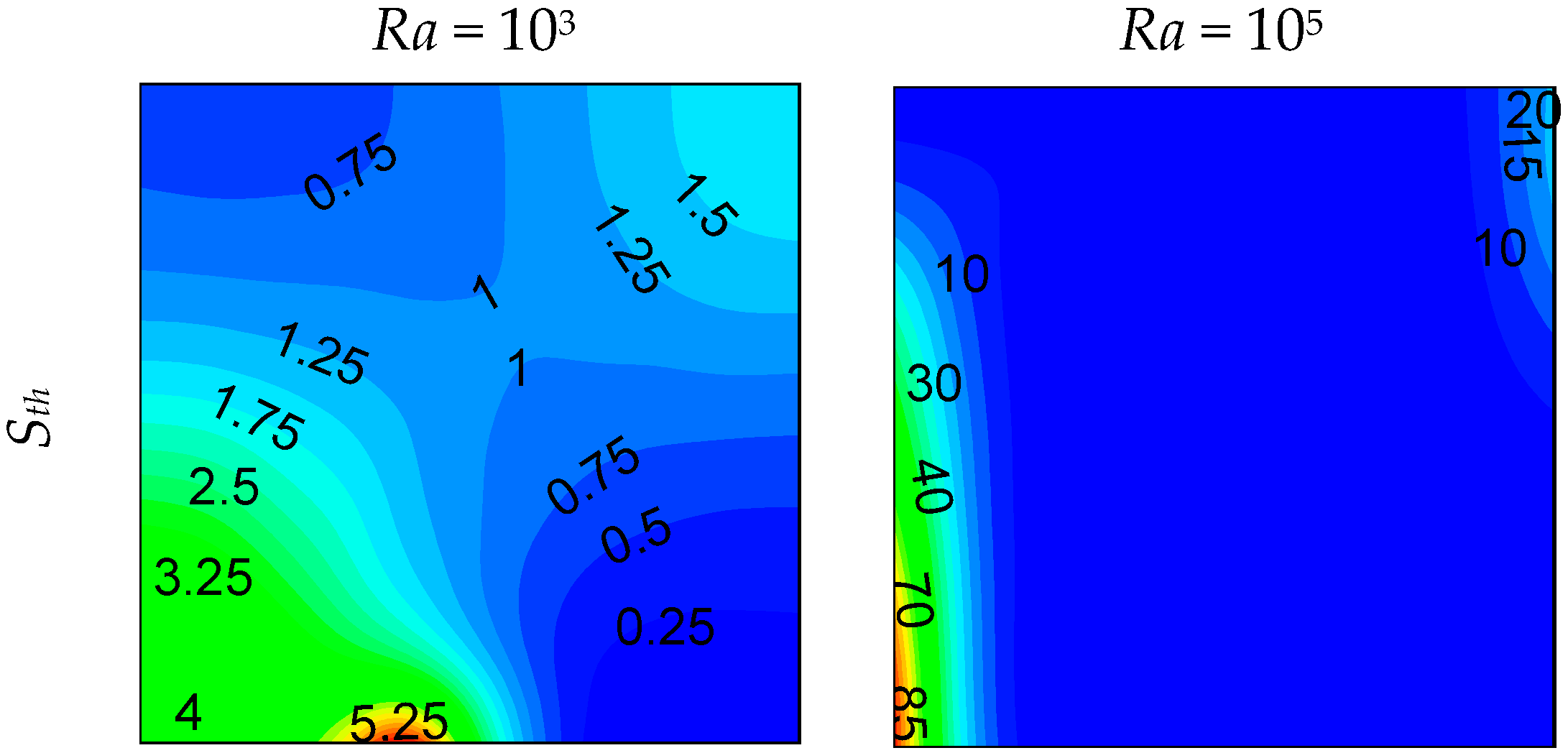
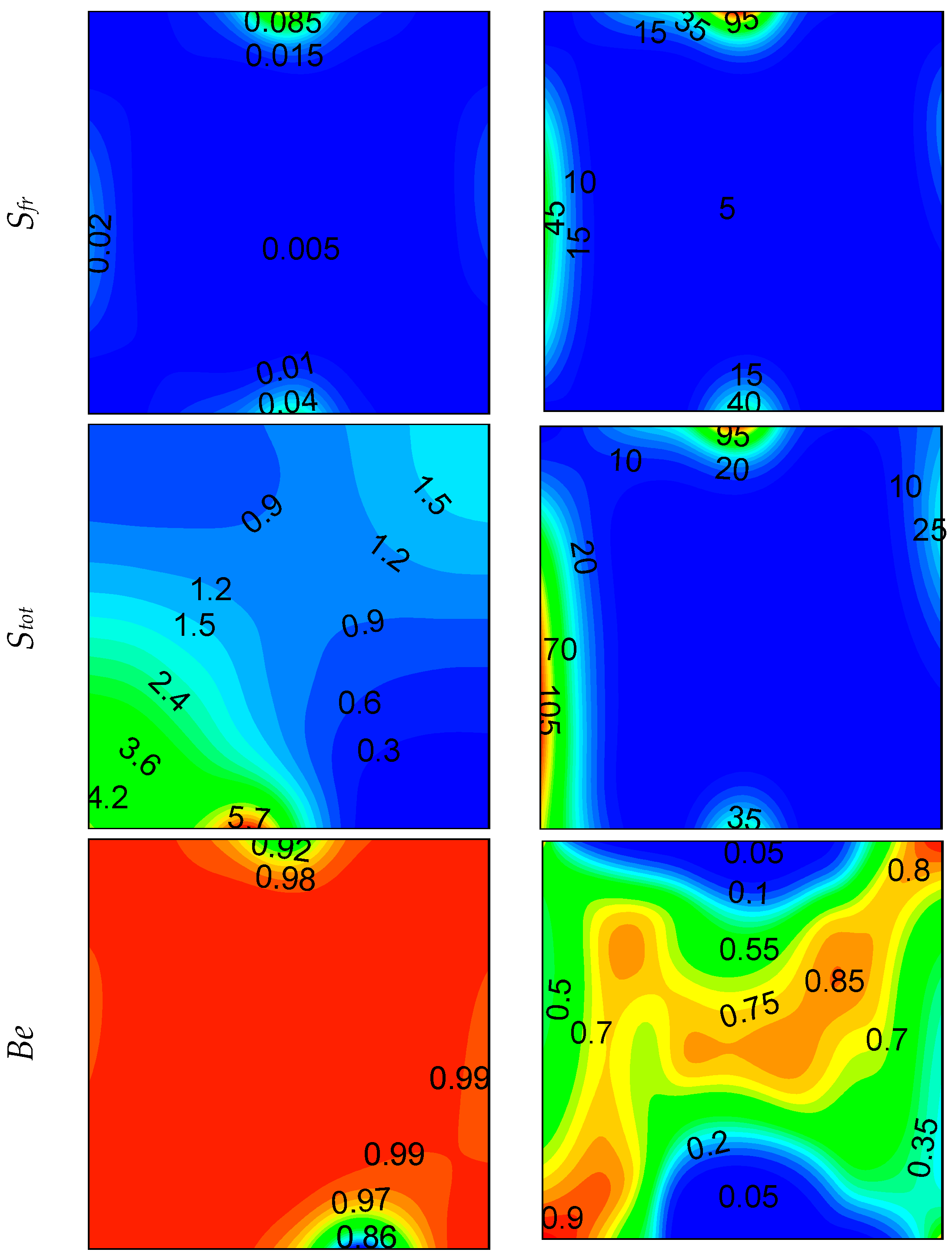
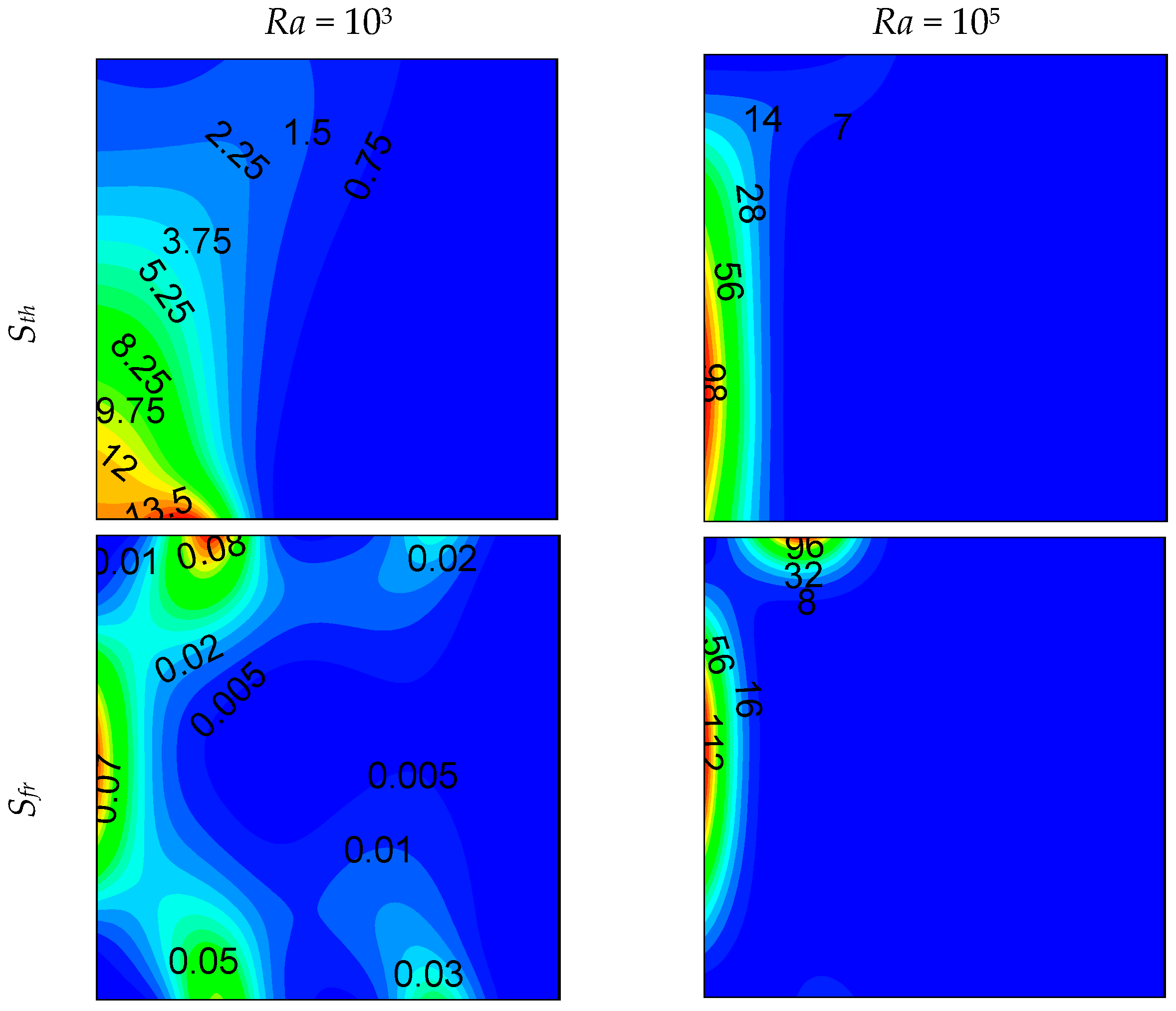
- Increasing the opening part increases the entropy generation almost linearly for lower values of the Rayleigh number.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Cp | Specific heat at constant pressure (J/kg·K) |
| d | Dimensionless opening width |
| g | Gravitational acceleration (m/s2) |
| h | Dimensionless opening length, h’/l’ |
| k | Thermal conductivity (W/m·K) |
| l | Dimensionless cavity width |
| Nu | Local Nusselt number |
| Nuav | Average Nusselt number |
| Pr | Prandtl number |
| Ra | Rayleigh number |
| t | Dimensionless time () |
| T | Dimensionless temperature [ |
| Cold temperature (K) | |
| Hot temperature (K) | |
| Dimensionless velocity vector () | |
| x, y, z | Dimensionless Cartesian coordinates (, , ) |
| Greek Symbols | |
| Thermal diffusivity (m2/s) | |
| Thermal expansion coefficient (1/K) | |
| Density (kg/m3) | |
| Dynamic viscosity (kg/m·s) | |
| Kinematic viscosity (m2/s) | |
| Dimensionless vector potential () | |
| Dimensionless vorticity () | |
| Dimensionless temperature difference | |
| Subscripts | |
| av | Average |
| x, y, z | Cartesian coordinates |
References
- Abib, A.H.; Jaluria, Y. Numerical Simulation of the buoyancy-induced flow in a partially open enclosure. Numer. Heat Transf. 1988, 14, 235–254. [Google Scholar] [CrossRef]
- Polat, O.; Bilgen, E. Laminar natural convection in inclined open shallow cavities. Int. J. Therm. Sci. 2002, 41, 360–368. [Google Scholar] [CrossRef]
- Bilgen, E.; Oztop, H. Natural convection heat transfer in partially open inclined square cavities. Int. J. Heat Mass Transf. 2005, 48, 1470–1479. [Google Scholar] [CrossRef]
- Bondareva, N.S.; Sheremet, M.A.; Oztop, H.F.; Abu-Hamdeh, N. Heatline visualization of natural convection in a thick walled open cavity filled with a nanofluid. Int. J. Heat Mass Transf. 2017, 109, 175–186. [Google Scholar] [CrossRef]
- Koufi, L.; Younsi, Z.; Cherif, Y.; Naji, H. Numerical investigation of turbulent mixed convection in an open cavity: Effect of inlet and outlet openings. Int. J. Therm. Sci. 2017, 116, 103–117. [Google Scholar] [CrossRef]
- Malekshah, E.H.; Salari, M. Experimental and numerical investigation of natural convection in a rectangular cuboid filled by two immiscible fluids. Exp. Therm. Fluid Sci. 2017, 85, 388–398. [Google Scholar] [CrossRef]
- Singh, D.K.; Singh, S.N. Combined free convection and surface radiation in tilted open cavity. Int. J. Therm. Sci. 2016, 107, 111–120. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Influence of magnetic field on nanofluid free convection in an open porous cavity by means of Lattice Boltzmann method. J. Mol. Liq. 2017, 234, 364–374. [Google Scholar] [CrossRef]
- Bondareva, N.S.; Sheremet, M.A.; Oztop, H.F.; Abu-Hamdeh, N. Heatline visualization of MHD natural convection in an inclined wavy open porous cavity filled with a nanofluid with a local heater. Int. J. Heat Mass Transf. 2016, 99, 872–881. [Google Scholar] [CrossRef]
- Oztop, H.F.; Kolsi, L.; Alghamdi, A.; Abu-Hamdeh, N.; Borjini, M.N.; Aissia, H.B. Numerical analysis of entropy generation due to natural convection in three-dimensional partially open enclosures. J. Taiwan Inst. Chem. Eng. 2017, 75, 131–140. [Google Scholar] [CrossRef]
- Oztop, H.F.; Al-Salem, K.; Varol, Y.; Pop, I. Natural convection heat transfer in a partially opened cavity filled with porous media. Int. J. Heat Mass Transf. 2011, 54, 2253–2261. [Google Scholar] [CrossRef]
- Hinojosa, J.F.; Buentello, D.; Xamán, J.; Tello, M.P. The effect of surface thermal radiation on entropy generation in an open cavity with natural convection. Int. Commun. Heat Mass Transf. 2017, 81, 164–174. [Google Scholar] [CrossRef]
- Hussain, A.K.; Mustafa, A.W. Natural convection in fully open parallelogrammic cavity filled with Cu–water nanofluid and heated locally from its bottom wall. Therm. Sci. Eng. Prog. 2017, 1, 66–77. [Google Scholar] [CrossRef]
- Singh, D.K.; Singh, S.N. Conjugate free convection with surface radiation in open top cavity. Int. J. Heat Mass Transf. 2015, 89, 444–453. [Google Scholar] [CrossRef]
- Bilgen, E.; Muftuoglu, A. Natural convection in an open square cavity with slots. Int. Commun. Heat Mass Transf. 2008, 35, 896–900. [Google Scholar] [CrossRef]
- Prakash, M.; Kedare, S.B.; Nayak, J.K. Numerical study of natural convection loss from open cavities. Int. J. Therm. Sci. 2012, 51, 23–30. [Google Scholar] [CrossRef]
- González, M.M.; Hinojosa, J.F.; Villafán-Vidales, H.I.; Bautista-Orozco, A.; Estrada, C.A. Theoretical and experimental study of natural convection with surface thermal radiation in a side open cavity. Appl. Therm. Eng. 2015, 75, 1176–1186. [Google Scholar] [CrossRef]
- Mohamad, A.A.; El-Ganaoui, M.; Bennacer, R. Lattice Boltzmann simulation of natural convection in an open ended cavity. Int. J. Therm. Sci. 2009, 48, 1870–1875. [Google Scholar] [CrossRef]
- Zamzari, F.; Mehrez, Z.; Cafsi, A.E.; Belghith, A.; Quéré, P.L. Numerical investigation of entropy generation and heat transfer of pulsating flow in a horizontal channel with an open cavity. J. Hydrodyn. 2017, 29, 632–646. [Google Scholar] [CrossRef]
- Mehrez, Z.; Bouterra, M.; Cafsi, A.E.; Belghith, A. Heat transfer and entropy generation analysis of nanofluids flow in an open cavity. Comput. Fluids 2015, 374, 214–224. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Mohammadi, F.; Abbasbandy, S.; Alhuthali, M.S. Entropy generation analysis for stagnation point flow in a porous medium over a permeable stretching surface. J. Appl. Fluid Mech. 2015, 8, 753–765. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Bhatti, M.M.; Abbas, M.A.; Ali, M.E.-S. Entropy generation on MHD blood flow of nanofluid due to peristalticwaves. Entropy 2016, 18, 117. [Google Scholar] [CrossRef]
- Abbas, M.A.; Bai, Y.; Rashidi, M.M.; Bhatti, M.M. Analysis of entropy generation in the flow of peristaltic nanofluids in channels with compliant walls. Entropy 2016, 18, 90. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Nasiri, M.; Shadloo, M.S.; Yang, Z. Entropy Generation in a Circular Tube Heat Exchanger Using Nanofluids: Effects of Different Modeling Approaches. Heat Transf. Eng. 2017, 38, 853–866. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M. Numerical study of entropy generation with nonlinear thermal radiation on magnetohydrodynamics non-newtonian nanofluid through a porous shrinking sheet. J. Magn. 2016, 21, 468–475. [Google Scholar] [CrossRef]
- Abbas, T.; Ayub, M.; Bhatti, M.M.; Rashidi, M.M.; Ali, M.-S. Entropy generation on nanofluid flow through a horizontal Riga plate. Entropy 2016, 18, 223. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, Y.; Qian, Y. Numerical study on entropy generation in thermal convection with differentially discrete heat boundary conditions. Entropy 2018, 20, 351. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, Z.; Qian, Y. A Numerical Study on Entropy Generation in Two-Dimensional Rayleigh-B´enard Convection at Different Prandtl Number. Entropy 2017, 19, 433. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, Z.; Qian, Y.; Guo, W. Study on Bifurcation and Dual Solutions in Natural Convection in a Horizontal Annulus with Rotating Inner Cylinder Using Thermal Immersed Boundary-Lattice Boltzmann Method. Entropy 2018, 20, 733. [Google Scholar] [CrossRef]
- Wei, Y.; Yang, H.; Lin, Z.; Wang, Z.; Qian, Y. A novel two-dimensional coupled lattice Boltzmann model for thermal incompressible flows. Appl. Math. Comput. 2018, 339, 556–567. [Google Scholar] [CrossRef]
- Kumar, P.; Eswaran, V. A Numerical Simulation of Combined Radiation and Natural Convection in a Differential Heated Cubic Cavity. J. Heat Transf. 2009, 132, 023501. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, Y.; Guo, Z. Numerical study of three-dimensional natural convection in a cubical cavity at high Rayleigh numbers. Int. J. Heat Mass Transf. 2017, 113, 217–228. [Google Scholar] [CrossRef] [Green Version]
- Wen, B.; Chini, G.P. Inclined porous medium convection at large Rayleigh number. J. Fluid Mech. 2018, 837, 670–702. [Google Scholar] [CrossRef]
- Wakashima, S.; Saitoh, T.S. Benchmark solutions for natural convection in a cubic cavity using the high-order time–space method. Int. J. Heat Mass Transf. 2003, 47, 853–864. [Google Scholar] [CrossRef]



| Ra | (center) | (center) | |
|---|---|---|---|
| 104 | 0.05528 (0.05492) | 1.1063 (1.1018) | 2.062 (2.062) |
| 105 | 0.034 (0.03403) | 0.262 (0.2573) | 4.378 (4.366) |
| 106 | 0.01972 (0.01976) | 0.1284 (0.1366) | 8.618 (8.6097) |
| Grid | Nuavg | |
|---|---|---|
| 613 | 7.62 | 135.442 |
| 713 | 7.6571 | 137.565 |
| 813 | 7.71246 | 141.871 |
| 913 | 7.724 | 142.913 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oztop, H.F.; A. Almeshaal, M.; Kolsi, L.; Rashidi, M.M.; E. Ali, M. Natural Convection and Irreversibility Evaluation in a Cubic Cavity with Partial Opening in Both Top and Bottom Sides. Entropy 2019, 21, 116. https://doi.org/10.3390/e21020116
Oztop HF, A. Almeshaal M, Kolsi L, Rashidi MM, E. Ali M. Natural Convection and Irreversibility Evaluation in a Cubic Cavity with Partial Opening in Both Top and Bottom Sides. Entropy. 2019; 21(2):116. https://doi.org/10.3390/e21020116
Chicago/Turabian StyleOztop, Hakan F., Mohammed A. Almeshaal, Lioua Kolsi, Mohammed Mehdi Rashidi, and Mohamed E. Ali. 2019. "Natural Convection and Irreversibility Evaluation in a Cubic Cavity with Partial Opening in Both Top and Bottom Sides" Entropy 21, no. 2: 116. https://doi.org/10.3390/e21020116
APA StyleOztop, H. F., A. Almeshaal, M., Kolsi, L., Rashidi, M. M., & E. Ali, M. (2019). Natural Convection and Irreversibility Evaluation in a Cubic Cavity with Partial Opening in Both Top and Bottom Sides. Entropy, 21(2), 116. https://doi.org/10.3390/e21020116









